笛卡尔方法论及解析思想在平面几何中的应用
2018-11-08李旭
李 旭
(辽宁省盘锦市辽河油田第三高级中学 124000)
方法论思想最初由法国数学家笛卡尔在《谈谈方法》一书中提出.在此摘取其中四条规则,作为本文讨论的核心.分别是:1.凡是我没有明确地认识到的东西,我决不把它当成真的接受;2.把我所审查的每一个难题按照可能和必要的程度分成若干部分,以便一一妥为解决;3.按次序进行我的思考,从最简单、最容易认识的对象开始,一点一点逐步上升,直到认识最复杂的对象;4.在任何情况之下,都要尽量全面地考察,尽量普遍地复查,做到确信毫无遗漏.结合高中考生所面对的问题,对以上四条简单说明.1.解决问题时只可用已知的定义、定理,不可盲目造定理;2.将完整复杂问题拆分成若干简单问题,逐个解决;3.分析条件,理清各对象之间的层级关系,最终将各低层级对象联系在一起解出题目;4.不可遗漏条件,检查.以下题为例,将上述理论思想用于实践.
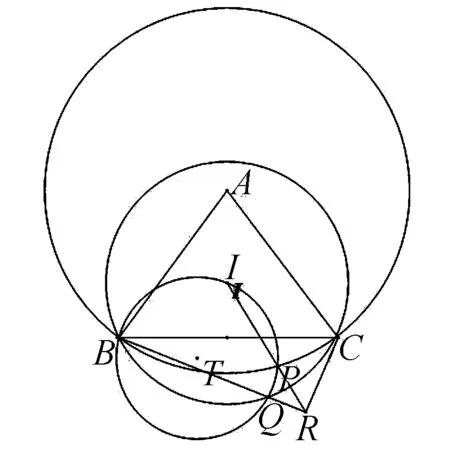
题目如图,在△ABC中,AB=AC,I为△ABC的内心.以AB为半径作圆A,以IB为半径作圆I,过点B,I的圆与圆A、圆I分别交于点P、Q(不同于点B).设IP与BQ交于点R.证明:BR⊥CR.(2017年全国高中数学联合竞赛加试第一题)
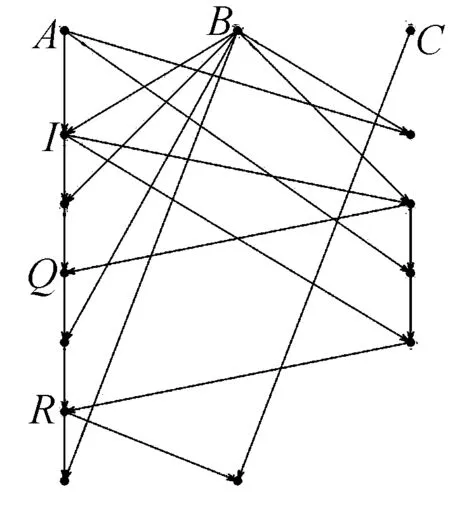
解析题干中所涉及各几何元素父对象、子对象关系如下图:
证明思路是:将要证明的命题,转换为各路径对应的简单问题,利用解析知识逐个解决,最终利用斜率证得垂直关系.
解法如下:
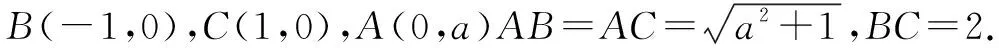
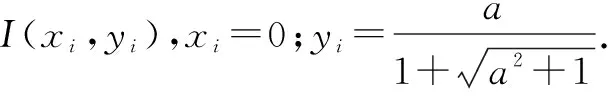
⊙A:x2+(y-a)2=a2+1;
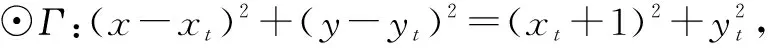
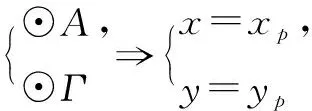
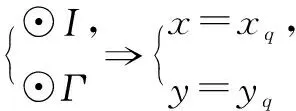
B(-1,0),Q(xq,yq),I(0,yi),P(xp,yp),
lBQ∩lIP=R,R(xr,yr),
在计算过程中, 参数为点A纵坐标a与圆Γ圆心横坐标xt,将其代入到方程组解中,得
经化简,kBR·kCR=-1,得证.
此解法与传统几何方法相比,思路较为简单清晰,但对应计算量较大,需要扎实的运算基础.两种解法各有利弊,在解题时可根据自身情况选择方案.
