例谈数形结合思想解决导数问题

王艺璇

(河北省唐山市第一中学 063000)

数形结合是数学解题中常用的思想方法，使用这种方法，很多问题能迎刃而解，且解法简捷.所谓数形结合，就是根据数与形之间的对应关系，通过数与形的相互转化来解决数学问题的一种重要思想方法.数形结合思想通过“以形助数，以数解形”，使复杂问题简单化，抽象问题具体化，能够变抽象思维为形象思维，有助于把握数学问题的本质，它是数学的规律性与灵活性的有机结合.

纵观近几年的高考试题，用数形结合的思想方法解决抽象的数学问题，成为高考命题的热点.数形结合思想在导数的应用主要体现在导数的几何意义的应用，下面以一道高考题为例来说明.

(2)用min{m,n}表示m,n中的最小值，设函数h(x)=min{f(x),g(x)}，讨论h(x)零点的个数.

解(1)设曲线y=f(x)与x轴相切于点(x0,0),则f(x0)=0,f′(x0)=0即

(2)分析：利用数形结合f(x)的图象不能确定，而g(x)的图象如图：因此欲找最小函数，只要在给定的区间上找最低函数曲线即可.如图1：

当x∈(1,+)时，g(x)=-lnx<0从而h(x)=min{f(x),g(x)}≤g(x)<0,

故h(x)在(1,+)上无零点，如图2：

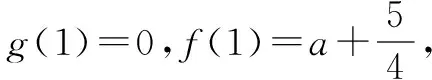
故x=1不是h(x)的零点.

当x∈(0,1)时，g(x)=-lnx>0，故只需考虑f(x)在(0,1)上的零点个数.

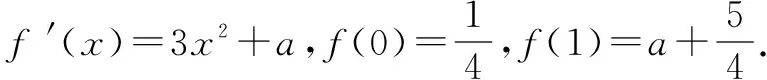
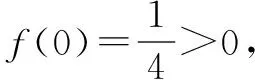
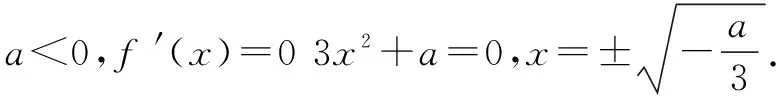
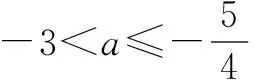
评析：此题考查了导数的几何意义，利用导数比较函数值得大小，考查了分类讨论思想及数形结合思想，考查综合分析问题解决问题的能力.

综上，数形结合是解决数学问题最重要的思想方法，特别是在高考导数题目中发挥着巨大作用.往往是在解决的全过程中，不断地通过数与形的结合，将抽象的问题具体化，通过图形找到解决问题的突破点，然后用数的推理去验证形的准确性，使解题过程达到顺畅通行！