与全称(或特称)命题真假有关的参数取值范围问题
—— 利用导数解决的方法
2018-11-08徐名琴
数理化解题研究 2018年28期
徐名琴
(新疆乌鲁木齐市新农大附中 830000)
一、参变分离,转化为最值问题
例1 若不等式4xlnx≥-x2+tx-2对x∈(0,+∞)恒成立,求实数t的取值范围.

二、分类讨论
如果无法分离参数,可以考虑对参数或自变量进行分类讨论求解.
例2 已知函数f(x)=lnx-mx2-4x(m≠0)存在单调递减区间,求实数m的取值范围.

当m>0时,g(x)=2mx2+4x-1为开口向上的抛物线,2mx2+4x-1>0总有正解;
当m<0时,g(x)=2mx2+4x-1为开口向下的抛物线,要使2mx2+4x-1>0总有正解,则Δ=16+8m>0,解得-2 综上所述,m的取值范围为(-2,0)∪(0,+∞). 若f(x)与g(x)的最值易求出,可直接转化为求f(x)与g(x)的最值比较. 若f(x)与g(x)的最值不易求出,可以有意识的放大观察问题的视角,将需要解决的问题,看作一个整体. 比如构造函数h(x)=f(x)-g(x),通过研究问题的整体形式,整体结构,并注意已知条件及待求结论在这个整体中的地位和作用,通过对整体结构的调节和转化使问题获解. 经检验,0 有些问题直接入手解决相当不易,尤其是对于唯一性或存在问题,可使用逆否命题等价转化法,更简捷. 解析g′(x)=3x2+(a+4)x-4.若g(x)在区间(m,3)上总为单调函数,则①g′(x)≥0在(m,3)上恒成立或②g′(x)≤0在(m,3)上恒成立.三、分而治之,各个击破


四、整体处理

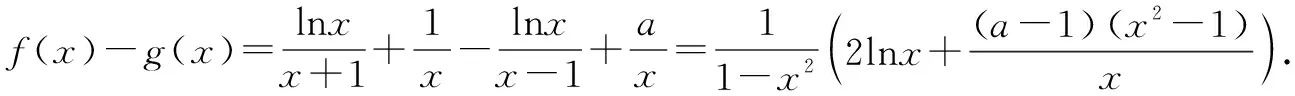
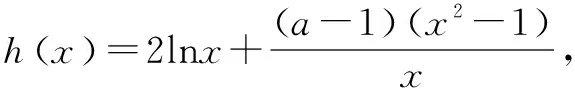

五、正难则反