棱锥外接球问题的几种求解策略
2018-11-08苏艺伟
苏艺伟
(福建省龙海第一中学新校区 363100)
以三棱锥和四棱锥为载体的外接球问题经常出现在各级各类的考试当中.笔者在多年的教学实践中总结出了五种求解策略,能够解决大部分三棱锥和四棱锥的外接球问题,整理如下.
策略1:找出该几何体的底面,将其水平放置,找出底面的中心(如果底面是三角形则找出外心),则球心和底面的中心连线必须和底面垂直.此法适用于较为简单的几何体外接球问题.

例1 已知三棱锥S-ABC的四个顶点都在球O的表面上,SC⊥面ABC,若SC=AB=AC=1,∠BAC=120°,则球O的表面积为____.

例2 已知一个几何体的三视图如图2,此几何体的外接球表面积为____.

策略2 在几何体中如果能够找到一个点,使得该点到几何体各个顶点的距离相等,则该点即为球心,此法同样适用于解决较为简单的几何体外接球问题.


例4 已知一个几何体的三视图如图(5),此几何体的外接球体积为____.


策略3 在该几何体中找出两个面,分别找出这两个面的中心,过这两个中心作出两条垂线分别和对应的面垂直,则这两条垂线的交点即为球心.

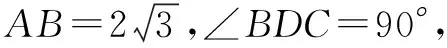
解析如图7所示,取BC中点P,连接AP,则AP⊥BC.
可知P为直角△CDB的外心,过点P作面CDB的垂线,设正△ABC的外心为Q,过点Q作面ABC的垂线,两条垂线的交点即为球心O.
例6 如图8所示,在棱形ABCD中,M为AC与BD的交点,∠BAD=60°,AB=3.将△CBD沿BD折起到△C1BD的位置.若点A,B,D,C1都在球O的球面上,且球O的表面积为16π,则直线C1M与面ABD所成角的正弦值为____.

解析如图9所示,可知△C1BD和△ABD是全等的正三角形.
设正△C1BD的外心为Q,过点Q作面C1BD的垂线,设正△ABD的外心为P,过点P作面ABD的垂线,两条垂线的交点即为球心O.



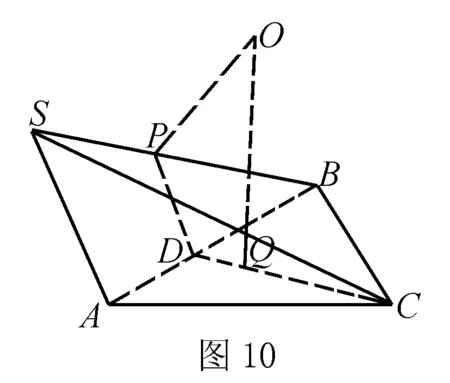

解析如图10所示,因为SA2+AB2=SB2,所以SA⊥AB.取SB中点P,AB中点D,连接PD,CD.
设直角△SAB的外心为P,过点P作面SAB的垂线,设正△ABC的外心为Q,过点Q作面ABC的垂线,两条垂线的交点即为球心O.


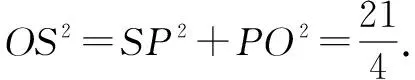
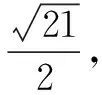
策略4 记住几种常用的几何体外接球模型可以事半功倍,迅速求解.
模型一棱长都相等的四面体的外接球
棱长都相等的四面体称之为正四面体,可以在正方体中找到一个与之对应的正四面体,换句话说可以将其补形成一个正方体.此时,正四面体的外接球即为该正方体的外接球,球心为正方体体对角线的中点, 体对角线等于球的直径.



模型二三条侧棱两两垂直的三棱锥的外接球
三条侧棱两两垂直的三棱锥可以补形成一个长方体,其外接球即为长方体的外接球.球心为长方体体对角线的中点,体对角线等于球的直径.
例9 已知三棱锥P-ABC中,PA=PB=PC=2,当三棱锥P-ABC的三个侧面的面积之和最大时,其外接球的表面积为____.
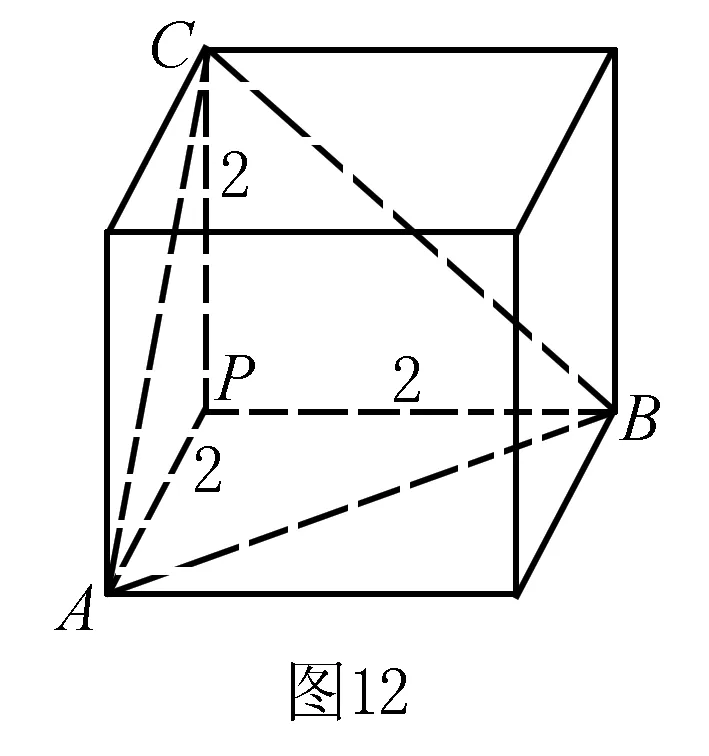


此时PA,PB,PC两两垂直.

模型三三组对棱分别相等的三棱锥的外接球
三组对棱分别相等的三棱锥可以补形成一个长方体,其外接球即为长方体的外接球.球心为长方体体对角线的中点,体对角线等于球的直径.

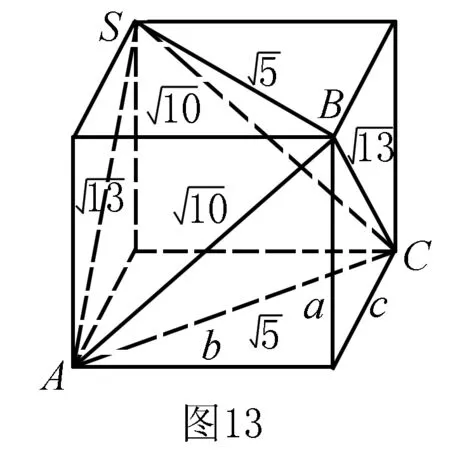
解析如图13所示,将该三棱锥补形成一个长方体,该三棱锥的外接球即为长方体的外接球.设长方体的长,宽,高分别为b,c,a.
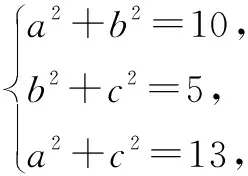
策略5 建系法.采用建系法求解,可以避开找球心这个难点,其步骤如下.
第一,将几何体中的几何要素整理清楚,弄清楚点,线,面之间的关系.
第二,建立适当的空间直角坐标系,求出落在球面上的各个点的坐标.
第三,设球心O(x,y,z),利用球心到球面上任意一点的距离都等于半径这个等量关系建立方程组.
第四,解方程组求出球心的坐标.进而算出半径,从而求出表面积或体积.
此法具有一定的程序性,解题规范,清晰明了,避免了寻找球心所带来的问题,效果甚好.
例11 一个三棱锥的三视图如图14,其中俯视图是等腰直角三角形.则该三棱锥的外接球体积是____.

解析如图15所示.易知该几何体为三棱锥P-ABC.其中PC⊥面ABC,AC⊥CB,AC=CB=PC=2.以C为原点建立空间直角坐标系.
则C(0,0,0),A(2,0,0),B(0,2,0),P(0,0,2).
设球心O(x,y,z),则有|OA|=|OB|=|OC|=|OP|=R.
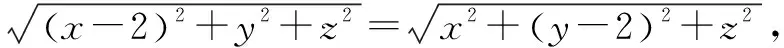


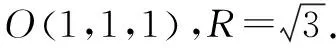

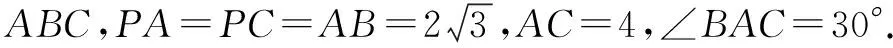
解析如图16所示.根据余弦定理易得BC=2.显然AB2+BC2=AC2,所以AB⊥CB.取AC中点N,连接PN,则PN⊥AC.由面PAC⊥面ABC,面PAC∩面ABC=AC,得PN⊥面ABC.作NT⊥AC,交AB于T.
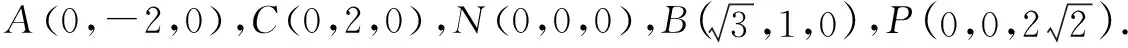
设球心O(x,y,z),则有|OA|=|OB|=|OC|=|OP|=R.
由|OA|=|OC|得
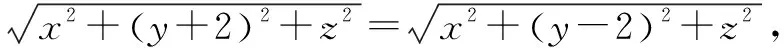
由|OA|=|OB|得

由|OA|=|OP|得
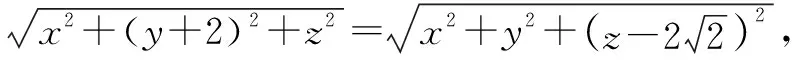
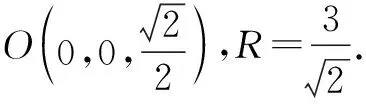
故球表面积是18π.
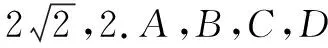
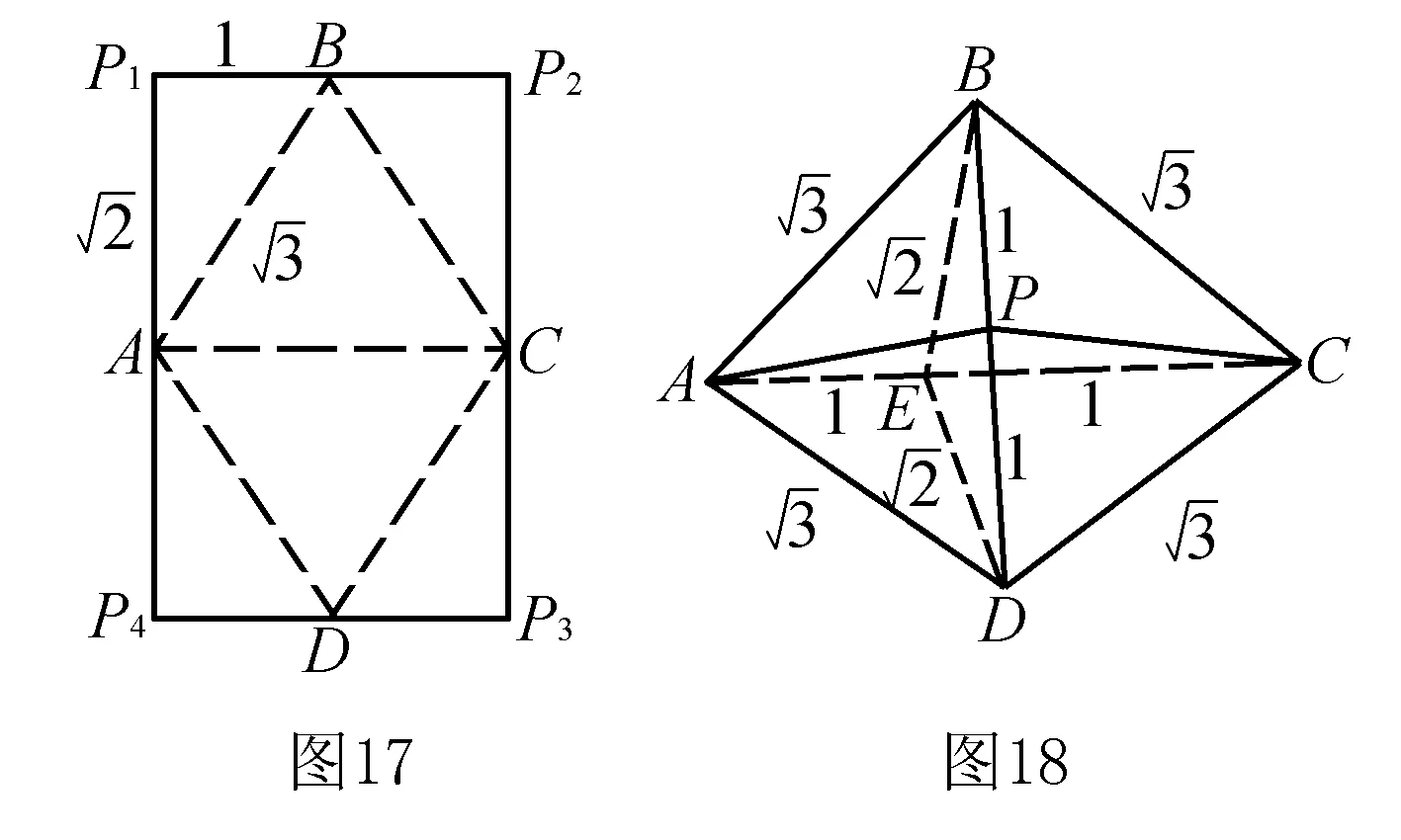
(1)该多面体是三棱锥;(2)面BAD⊥面BCD;(3)面BAC⊥面ACD;(4)该多面体外接球的表面积为5π.
解析如图18所示,该几何体为一个三棱锥B-ACD,点P为BD中点,各棱长度如图所示.取AC中点E,连接BE,DE,则BE⊥AC,DE⊥AC,故∠BED即为二面角B-AC-D所成的平面角.由于EB2+ED2=BD2,所以
∠BED=90°,故面BAC⊥面ACD.同理可证∠APC=90°,故面BAD⊥面BCD.
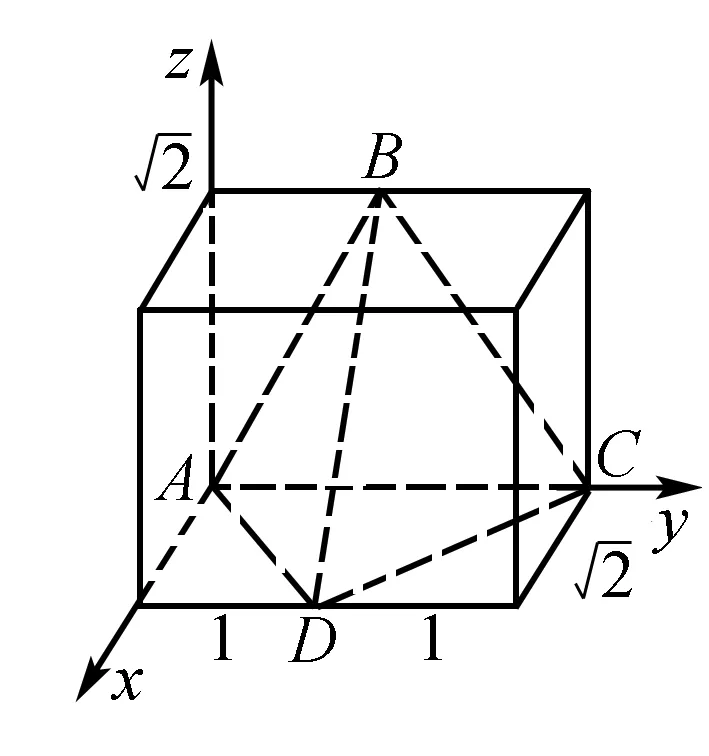
图19
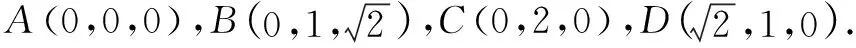
设球心O(x,y,z),则有|OA|=|OB|=|OC|=|OD|=R.
由|OA|=|OB|

由|OA|=|OC|

由|OA|=|OD|


故此三棱锥的外接球表面积是5π.
