基于分层逼近算法的异型钢模快速优化设计研究
2018-11-08谭志银
谭志银
滁州职业技术学院机电工程系,滁州,239000
钢模具有强度大、制造成本低、可重复使用性好、形式多样等优点,在各类建筑施工中被广泛使用[1-3]。如在对地铁隧道进行混凝土浇筑施工前,需设计出能一次成型顶梁和弧形侧面的组合式钢模,该组合式钢模由顶部的平面钢模和侧部的异型钢模组成(图1),本文对其中的异型钢模进行优化设计,以减少钢材用量,降低成本。

图1 某地铁隧道工程的局部横断面
既能快速响应客户的需求,又能保证产品性能的可靠性,是目前定制产品、优化设计面临的问题。由此,祖耀等研究了行为和机构在功能——结构转换过程中的桥梁作用,并由此提出了行为和机构映射关系网下基于迭代的FBMS模型[4]。马军等根据系列产品的相似性特点,结合参数化设计思想建立系列产品主模型,开发出基于有限元参数化语言的有限元主文档,在系列产品的设计参数值发生变化时能够自动进行有限元分析,实现了系列产品的快速优化设计[5]。但上述算法应用在异型钢模优化设计时,其计算速度仍较慢。本文提出了一种能提高运算速度的结构优化设计算法——分层逼近算法,并将此算法应用在异型钢模设计过程中,达到了快速优化设计的目的。
1 设计结构模型
结合图1施工要求,设计出图2所示的异型钢模,其最外侧为与待浇筑层的侧面形状相同的整体式钢板,包括上部斜面2和下部弧面1;在下部弧面1的内侧面上,焊接有呈十字交叉状的横筋4、纵筋3,以提高钢板强度。在上部斜面2的顶端,焊接有活动铰链座6,可与其他钢模构成活动铰链;在下部弧面1的中部,焊接有斜撑安装座5,用于与斜向支撑油缸连接。此外,为了防止漏浆,下部弧面1的底端7还向下延伸一段距离。

图2 异型钢模的模型
本设计模型中存在着S个交叉焊接点(S为纵向支撑筋数目),其中绝大部分是由四个角焊缝构成的双T型焊接头。双T型焊接头具有刚度大、变形小的特点,能显著提高弧形钢板的强度。
2 确定结构参变量
对图2进行受力分析,可得图3。由图3可知,异型钢模的负载主要有:斜面混凝土压力q1、弧面压力载荷q、侧部支撑力F0、顶端活动铰链座反力(Rx,Ry)、钢模自重 G0、浇筑时的冲击载荷 C[6]。其中,斜面混凝土压力q1:

式中:Kc为综合折算系数,可取1.3~1.4;ρ为混凝土密度(kg/m3);h1为自斜面底部的高度(m)且h1≤ 0.2。
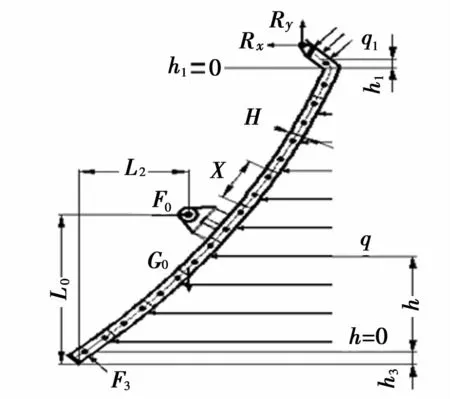
图3 受力分析图
钢板面压力载荷q:

式中:h为自弧面底部的高度(m),且h≤2.1。
钢模自重G0:

式中:L为斜面宽度(m);L4为单根横筋长度(m),L4=θR(Q-1);L3为单根纵筋长度(m),L3=6;Gg为整体钢板重量(N);Gh为单根横筋重量(N);Gc为单根纵筋重量(N);Ac为纵筋型钢截面面积(cm2);Ah为横筋型钢截面面积(cm2);δ为钢板厚(mm);ρ2为钢材密度(kg/m3);J为横筋排数;Q为纵筋数量;R为弧半径(m),θ为弧形钢板的弧度(rad),初始值为0.523。
为了简化计算,横筋、纵筋可选相同型号的热轧槽钢,且背靠背布置。设热轧槽钢截面面积为A,则钢模自重G0:

因此,设计参变量有4个,组成参变量矩阵为:

考虑结构特点和可选钢材的型号,初定出上述参变量的结构约束条件为:

3 设计优化算法
3.1 逐次迭代算法的局限性
异型钢模的结构优化设计需同时满足:(1)其工作应力及应变不得超过材料容许值;(2)其总重量最小化[7]。
因此,异型钢模的结构优化设计标准为:σ≤[σ]=160 MPa;ω—≤ [ω—]=5 mm。
利用有限元分析功能的CAD软件,如Ansys、SolidWorks、Abaqus,可作为结构优化设计的辅助工具[7,8]。
但上述CAD软件中的结构优化设计功能均基于逐次迭代算法,即从一组初始的参变量开始逐步改变参变量,直到总重量最小化,所有限制条件都能够符合为止。每次迭代,结构模型都会根据参变量的改变而改变,所以每次迭代都必须做至少一次的有限元分析。
例如,本文所述的异型模板模型,需执行2 560次迭代有限元计算,单次计算至少180 s,至少需128 h才能完成,耗时过长。同时,利用软件进行逐次迭代计算优化设计,对参数化模型品质要求非常严格,细微的建模错误即可导致计算失败。
3.2 分层逼近算法
对于多参变量的结构优化设计问题,也可以理解成最轻设计问题,而最轻设计问题必须满足的条件是:当任何一个自由参变量作单位变化时,结构的刚度收益和重量支出的比值应彼此相等,即都等于某一常数[9,10]。在最轻结构中,自由参变量均被调整到具有相等的优化效率,意味着对结构刚度贡献大的参变量应多负重量,并优先设计。
因此,可对多参变量的结构设计问题设计如下算法:若能确定结构参变量对结构刚度贡献大小关系,则可按顺序关系先确定出贡献最大的,再依次确定其他参变量;若无法得出结构刚度贡献大小顺序关系,则先按排列组合方法,假定出多种顺序关系,依次确定出各种顺序关系下的各参变量,并计算每种情况的模型质量,取最小质量的模型参变量,即为最优解。本文称此算法为分层逼近算法。
3.3 异型钢模的优化设计算法
分析图2、图3可知:钢板厚δ对结构刚度贡献最大,其次是型钢截面面积A,最后是纵筋数量Q和横筋排数J。故应先确定钢板厚δ,再依次确定其余参变量。
在确定某单一参变量时,可采用如图4所示的二分逼近法,即:从最大Smax和最小Smin两个极端情况,向中间逐次靠拢逼近。二分逼近法,可迅速计算出某参变量的初始约束条件是否合理,同时也可减少确定单个参变量的计算次数。

图4 单参数二分逼近法流程图
基于单参数二分逼近法和分层逼近算法,进一步设计出如图5所示的异型钢模的优化设计流程。利用此算法流程,最多需19次即可得到最优解。与传统逐次迭代算法的2 560次计算相比,分层逼近算法的计算效率明显提高。

图5 异型钢模的优化设计流程图
4 分层逼近算法
为了实现图5所示的全参变量优化设计流程,需要对图2中的异型钢模模型建立参变量化模型,同时还需要设计出相应的应力分析算法。利用Solid Works软件可实现上述功能[11,12]。
4.1 参变量化模型
在模型中的“方程式”中,分别建立上述参变量的全局变量,其中型钢截面面积A分解为槽钢高度h、槽钢宽度b、槽钢底厚t、槽钢宽厚d等四个简化参数。相应的参变量化建模参变量输入界面如图6所示。
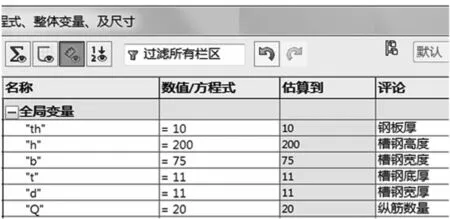
图6 参变量化建模参变量输入界面
同时,将图2的活动铰链座、斜撑安装座等结构均予以删除,以简化模型,提高计算速度,简化后的模型图如图7所示。

图7 模型简化图
4.2 静应力算例设计
在SolidWorks软件中,从“SolidWorks插件”中选择“SolidWorks Simulation”,在“Simulation”界面中,依次选择“算例顾问”→“新算例”→“静应力分析”[13],在“静应力分析”中,依次对“新模型”“连结”“夹具”“外部载荷”“网格”等内容进行设定,以完成静应力算例设计。
在“夹具”设定中,将异型钢模的顶部、底部均设定为全固定模式,将斜撑安装座处设定为分割固定模式;在“新模型”中,零件材料设为 1.003 7(S235JR);在“连接”中,将零部件接触的接触类型设为“接合”。
在“外部载荷”设定中,将斜面、弧面的载荷均设定为“非均匀载荷”,并对“类型”“坐标”“坐标轴系”“编辑方程式”等项进行设置。相应的设置结果分别如图 8(a)(b)所示。
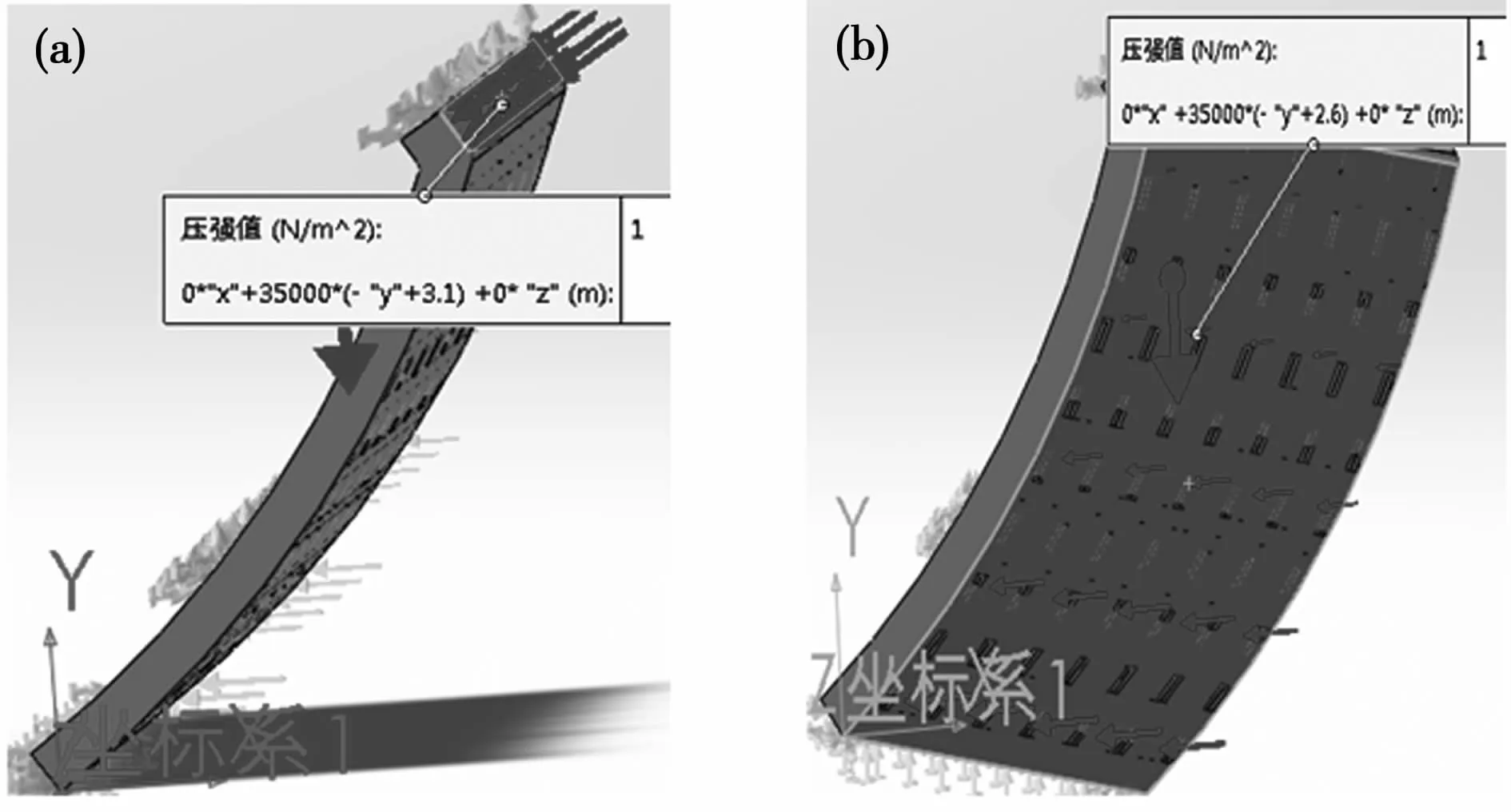
图8 “外部载荷”设置图
对图8进行“网格化”设置,如图9所示。

图9 网格化的模型图
4.3 计算结果
按照全参变量优化设计算法流程,对图9依次进行全参变量二分逼近法优化计算,各算例顺序和算例结果如表1所示。在实施过程中,若在改变参变量出现建模错误时,需作适应性调整。

表1 二分逼近法计算结果
由表1可知,本例中,只需8次静应力强度计算,用时不超过1 h,即可得出最优化的参变量(算例5),其计算结果如图 10(a)(b)所示。
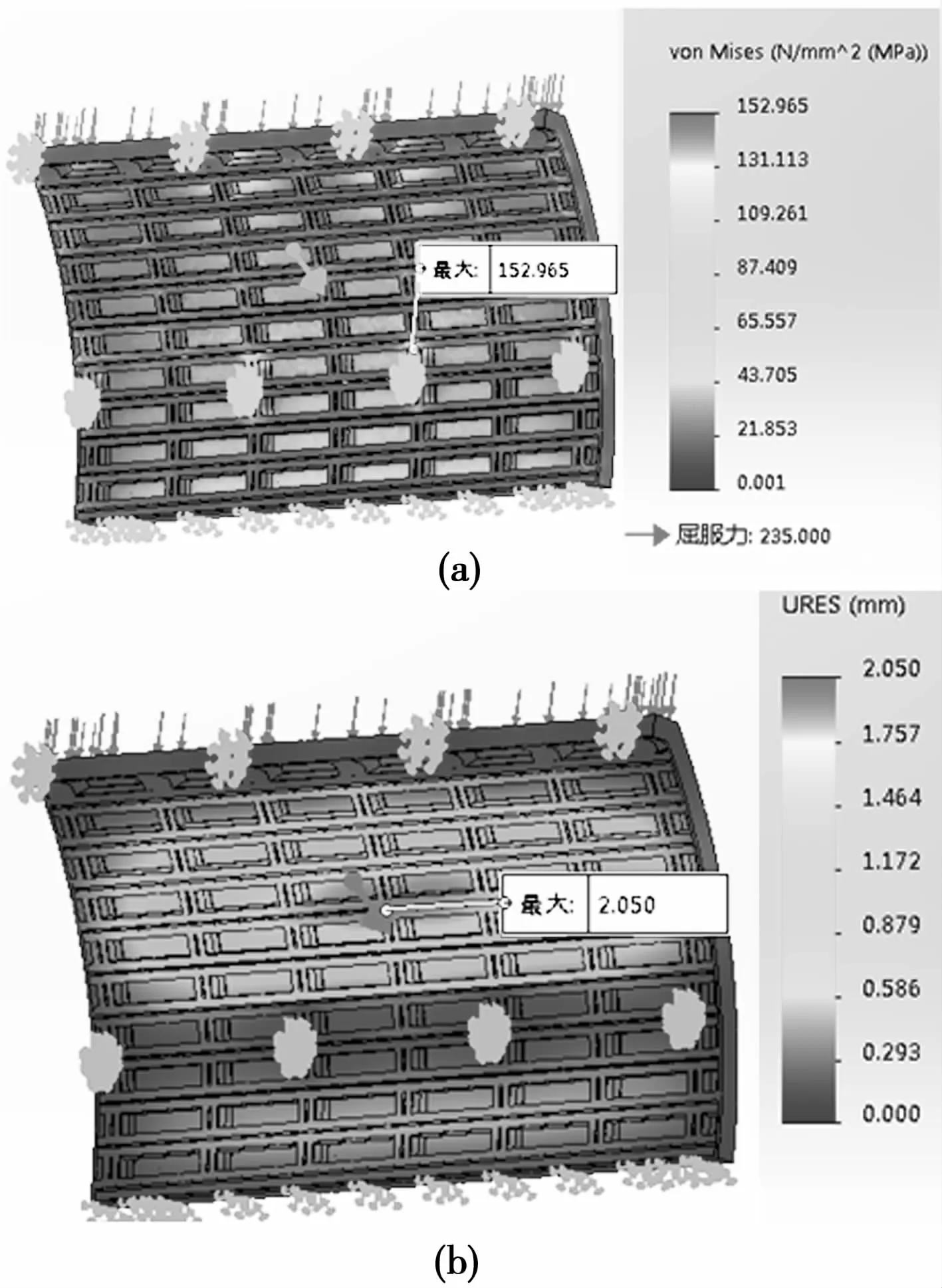
图10 优化设计计算结果
由计算过程可知,与逐次迭代法相比,采用分层逼近算法进行结构优化设计,计算次数和用时大幅度减少,计算速度快。
5 结语
本文提出的分层逼近算法,计算速度快,可应用在异型钢模结构优化设计过程中。在优化设计前,需根据使用要求,分析并得出异型钢模的结构参变量及约束条件;利用建模软件,建立参变量化的结构模型和静应力算例。在具体优化设计时,需利用分层逼近算法产生算例计算顺序,分步顺序逼近进行静应力强度计算,比较并得出优化解,即可完成异型钢模的结构优化设计。
