岩石爆破损伤范围及损伤分布特征模拟分析
2018-11-08黄佑鹏王志亮毕程程
黄佑鹏,王志亮,毕程程
(合肥工业大学土木与水利工程学院,安徽合肥 230009)
爆破开挖在隧道掘进和煤岩开采等诸多方面应用普遍,具有快速高效的优点。炸药爆炸一般在极短时间内产生很高压力,通过应力波和爆生气体综合作用使岩石发生破碎[1]。由于炸药性能、装药结构、介质性质、地质条件等因素的复杂性,爆破效果可控性不高,容易产生不利影响,如爆炸波对预保留岩石的损伤效应会降低施工质量,影响工程安全。因此,为了合理分析和有效控制岩石动态损伤,必须对岩石爆破问题进行深入研究。
岩石爆破损伤指的是爆炸荷载作用下岩石的破坏效应,即岩石的压碎和开裂。通常采用变量D来描述损伤程度,D=1表示岩石完全压碎,D=0表示岩石完整。岩石爆破中,一般根据岩石破坏程度,以炮孔为中心由近及远依次分为压碎区、裂隙区和弹性震动区[1],而工程中重点关注的是压碎区和裂隙区。迄今,国内外研究人员均对爆破损伤开展了大量研究:左双英等[2]通过模拟隧道爆破开挖,探讨了爆破诱发的质点振动衰减特征及围岩损伤分布规律,并预估岩体开裂深度和爆破损伤影响范围;周燕等[3]对台阶爆破相邻炮孔间损伤范围进行模拟研究,得出两孔间损伤百分比随孔距增大而减小随后趋于定值的结论;胡英国等[4]通过自定义拉压损伤定量计算模型,对溪洛渡高边坡保留岩体的爆破开挖损伤效应进行了数值模拟;杨建华等[5]研究分析了隧洞开挖重复爆炸荷载作用下围岩的累计损伤特性;Yu等[6]研究了钻爆法对砂岩的破坏效应,指出砂岩的损伤程度随加载速率增加而增加;戴俊[7]利用Mises强度准则,并考虑岩石三向受力及其强度的应变率效应,导出柱状药包爆炸岩石压碎圈与裂隙圈半径计算公式;Esen等[8]基于压碎圈指数,提出了压碎区范围的计算公式;Sim等[9]通过裂纹扩展准则和气体质量守恒模拟岩石裂隙扩展,并基于裂隙应力强度因子来确定裂隙扩展长度。就研究方法而言,由于爆破试验成本较高、耗时长,目前采用数值分析程序来模拟岩石的爆破损伤仍是一种简便高效的研究方法。
在实际工程中,由于工况不同,爆破施工的岩石种类不一,因而岩石的破坏效果必然有所差异。例如,在进行光面爆破施工时,必须严格控制预保留岩体的破坏程度,尤其是炮孔附近岩体的局部损伤。为了合理预估和控制爆破效果以提高施工质量,就必须对不同岩石的爆破损伤加以区别对待。但在已有研究成果中,针对不同岩石爆破损伤分布特征差异性的研究尚不多见。本文基于LS-DYNA有限元软件和HJC(Holmquist- Johnson-Cook)本构模型,从损伤变量的角度对一种和多种岩石中单孔爆破进行模拟分析。首先,针对石灰岩材料,采用不耦合装药方式,探究爆破损伤范围随不耦合装药系数K增大的变化规律;其次,采用耦合装药方式,分别对石灰岩、凝灰岩和花岗斑岩3种岩石材料进行爆破损伤模拟,分析比较不同岩石爆破损伤的分布规律,力求得出对实际工程有参考价值的结论。
1 材料本构模型及数值建模
1.1 材料本构模型
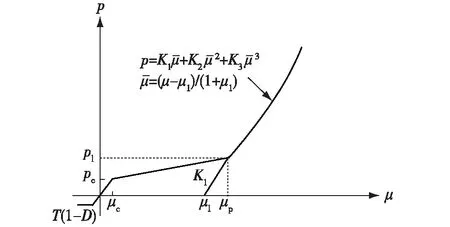
图1 HJC模型状态方程曲线Fig.1 Equation of state curve of HJC model
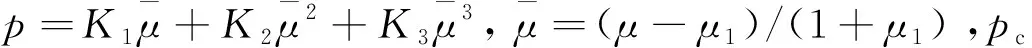
HJC模型的屈服面方程为:
(1)
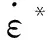
HJC模型用等效塑性应变和塑性体积应变的累计来描述材料损伤,其损伤演化方程为:
(2)
(3)

表1 石灰岩HJC模型参数Tab.1 Parameters of HJC model for limestone
1.1.2炸药材料 炸药采用LS-DYNA程序中内置的*MAT_HIGH_EXPLOSIVE_BURN高性能炸药材料模型和JWL状态方程,描述爆炸过程中爆炸产物的体积、压力以及能量特性,其表达式为:
(4)
式中:P为爆轰压力;V为相对体积;E0为初始比内能;A,B,R1,R2,ω为材料常数。选用2#岩石乳化炸药,各参数取为:密度ρ=1 150 kg/m3,爆速D= 3 500 m/s,A=214.4 GPa,B=0.182 GPa,R1=4.2,R2=0.9,ω=0.152,E0=4 190 MJ/m3,V=1.0。
1.1.3空气材料 空气采用空物质材料模型*MAT_NULL,以线性多项式*EOS_LINER_POLYNOMIAL表示其状态方程:
P=C0+C1V+C2V2+C3V3+(C4+C5V+C6V2)E0
(5)
式中:C0~C6为方程相关参数。其中,C4=C5=0.4,E0=2 500 MJ/m3,V=1.0,余下参数均为0。
1.2 数值模型
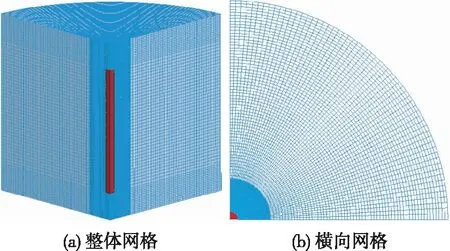
图2 数值计算模型Fig.2 Numerical calculation model
对岩石单孔爆破进行数值模拟,设置不耦合装药和耦合装药两种方式。考虑到岩石、炸药和空气3种材料的相互作用,且为了避免网格畸变导致计算困难的问题,采用流固耦合算法,即岩石采用Lagrange算法,炸药和空气采用ALE算法。为减少计算量,根据对称性,建立1/4圆柱模型(图2)。岩石半径80 cm,高度100 cm,孔径根据不耦合系数调整;装药长度70 cm,半径3 cm;炮孔堵塞长度15 cm,且为简化模型,堵塞物和岩石采用相同材料;空气耦合区域半径15 cm。在圆柱面外侧和底面设置透射边界条件模拟无限域岩石介质,在对称面上施加法向位移约束。炸药起爆方式为整体同时起爆。
2 数值模拟结果与分析
2.1 不耦合装药下岩石爆破损伤范围
针对石灰岩材料,根据上述建模方法,分别采用不耦合装药系数K=1.1~3.2进行爆破损伤模拟。设定计算时间为1.0 ms(损伤演化已基本稳定[13]),时间步长取5.0 μs。将模型镜像后形成整体模型,可得到炮孔中部岩石横向剖面的损伤分布情况。石灰岩损伤分布与不耦合系数的关系见图3。
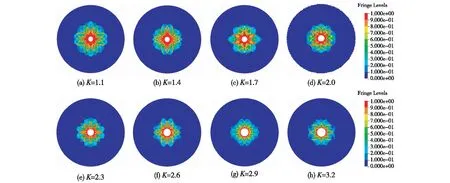
图3 石灰岩损伤分布与不耦合系数K的关系(t=1 ms)Fig.3 Relationship between distribution of limestone damage and uncoupling coefficient K (t=1 ms)
由图3可见,损伤D随炮心距增加均大致呈由大到小的分布规律,炮孔附近岩石完全损伤,即D=1(图3中红色区域)。损伤主要以放射状裂隙形式向外发展,随着不耦合系数K的增加,压碎区和裂隙区范围呈现逐渐减小趋势。
戴俊[7]基于爆炸荷载作用下岩石的破坏准则,提出柱状装药条件下炮孔四周压碎圈和裂隙圈半径的理论计算公式。耦合装药条件下,压碎圈半径为:
(6)
不耦合装药条件下,压碎圈半径为:
(7)
两种装药条件下,裂隙圈半径为:
(8)

由于岩石种类、地质构造等诸多因素影响,目前难以得到准确统一的爆破损伤范围的确定方法。国内外研究学者通过大量研究,提出岩石爆破压碎区和裂隙区范围的估计方法。对于压碎区范围,郭文章等[14]认为粉碎区半径与装药半径之比d=2~3,林秀英[15]认为d=3~7,哈努卡耶夫[16]认为d=2~3,Donze等[17]认为d≈5;对于裂隙区范围,哈努卡耶夫认为裂隙区半径为装药半径10~15倍,戴俊[7]通过计算,得出几种常见岩石的裂隙区半径与炮孔半径之比大致在10~15。综合以上研究成果,可大致认为,岩石单孔爆破压碎区半径R1与装药半径r之比为2~7,裂隙区半径R2与装药半径r之比为10~15。
根据图3模拟结果,在90°范围内每隔9°提取相同炮心距岩石单元的损伤并取其平均值,以此值作为该炮心距处岩石损伤值。岩石中爆炸波作用范围很大,文献[18]认为可达(120~150)r。由于炮心距较远时岩石损伤程度很低,一般不影响工程质量和安全,故作者认为D<0.05时,损伤可忽略不计,并以此方法确定出裂隙区范围。计算结果与其他方法所确定损伤范围的对比见表2。可以看出本文模拟结果较为合理。

表2 不同方法得到的爆破损伤范围比较Tab.2 Comparison of blasting damage ranges given by different methods
如图4所示,以K=1.1为例,得到压碎区边界岩石单元的应力时程曲线,其峰值应力为194 MPa。通过理论公式[7]计算得到压碎区边界岩石最大应力为207 MPa,与模拟值接近,进一步验证了本文所模拟结果的准确性。图5为压碎区半径与炮孔半径之比R1/rb和裂隙区半径与炮孔半径之比R2/rb随不耦合系数K增大的变化曲线。可以看出,随着不耦合系数逐渐增大,R1/rb与R2/rb均呈先快后慢的减小趋势,且裂隙区范围减小速率要大于压碎区。
当K>2.0时,R1/rb≈1,此时岩石压碎区很小,可忽略不计。该规律在光面爆破技术中有所体现,且与文献[19]得出的光面爆破不耦合装药系数宜采用2~3的结论相符。综上分析可知,合理增大不耦合装药系数,能够有效地减小炮孔周围岩石的损伤范围。
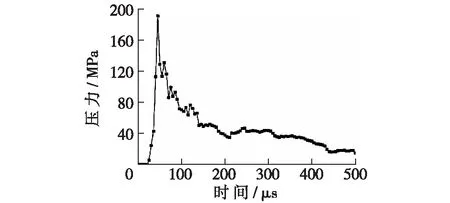
图4 压碎区边界压力时程曲线(K=1.1)Fig.4 Time-history curves at boundary of crushed zone
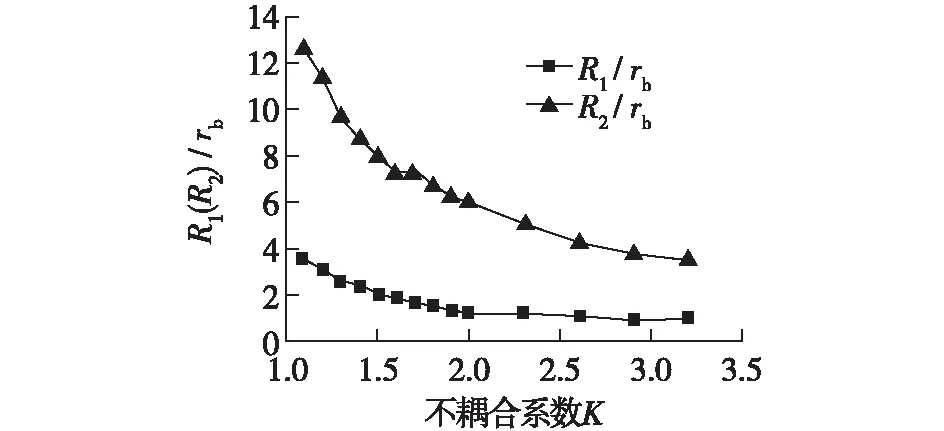
图5 随不耦合系数K变化的损伤范围Fig.5 Change of damage range with uncoupling coefficient K
2.2 不同岩石爆破损伤分布规律
由于实际爆破工程中岩石种类不一,各种岩石物理力学特性存在差异,因此需要针对不同岩石研究其爆破损伤空间分布规律的差异性,以便合理预测和控制损伤。建模方法同上,分别采用石灰岩[11]、凝灰岩[11]和花岗斑岩[12]的HJC材料模型进行模拟,其中部分参数见表3。装药方式为耦合装药。沿炮孔中部横截面上的岩石损伤分布如图6所示。

表3 岩石的部分HJC模型参数Tab.3 Partial parameters of HJC model for rocks
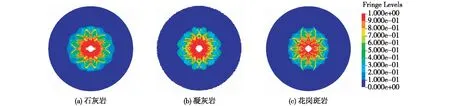
图6 不同岩石爆破损伤分布(t=1 ms)Fig.6 Distribution of blasting damage for different rocks (t=1 ms)
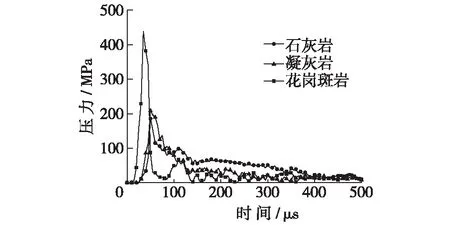
图7 压碎区边界岩石压力时程曲线(K=1.0)Fig.7 Time-history curves of pressure at boundary of rock crushed zone (K = 1.0)
从图6可见,3种岩石的爆破损伤程度都呈现出随炮心距增加而逐渐减小的分布规律,符合岩石爆破破坏的形态特征。从裂隙发展看,石灰岩、凝灰岩和花岗斑岩裂隙均发展明显,其中花岗斑岩裂隙多而密;从压碎区与裂隙区过渡看,石灰岩和凝灰岩过渡界线相对清晰,而花岗斑岩过渡界线不甚明显。图7对比了3种岩石压碎区边界单元压力时程曲线,可以看出,石灰岩和凝灰岩峰值比较接近,花岗斑岩峰值约为前者两倍。
采用上文相同的损伤值获取方法,获得不同炮心距岩石的损伤度。3种岩石损伤度D随炮心距l在空间上的分布如图8所示。根据损伤度衰减趋势,采用“S”形曲线的Logistic函数进行拟合,D与l的函数关系表达式为:
(9)
式中:K0,a,b为相关参数。
图8中曲线拟合度均达到0.99,说明拟合效果较好。Ⅰ,Ⅱ,Ⅲ分别表示岩石压碎区(完全损伤)、裂隙区(部分损伤)和弹性震动区(未损伤)。采用前文相同的方法确定损伤半径,结果见表4。

表4 不同岩石损伤范围Tab.4 Damage scopes of different rocks
从图8可看出,损伤分布曲线均大致呈现反“S”形。Fakhimi等[20]通过研究爆生气体对裂隙扩展作用,得出气体密度随炮心距增加的分布曲线,以此反映裂隙分布,其趋势与本文中的曲线趋势相符。从压碎区范围看,石灰岩和凝灰岩的范围大小接近,且明显大于花岗斑岩;从损伤曲线衰减特征来看,石灰岩和凝灰岩的损伤曲线在压碎区之后迅速下降,而花岗斑岩的损伤曲线先是缓慢下降,然后快速下降。前者表现出压碎区与裂隙区过渡界限明显的特征,而后者表现出过渡界线不明显的特征,这与前文通过图6的损伤云图直观分析得到的结论一致。分析其原因,石灰岩和凝灰岩的动态强度特性较为接近,在高温高压下易产生较大范围的压碎和开裂;花岗斑岩属于火成岩,特性与花岗岩类似,具有较高的动态强度,爆炸荷载下不易产生压碎性破坏,而多产生裂纹。因此,在实际爆破工程中,应根据岩石种类特性的不同,充分考虑不同岩石爆破损伤分布的差异性。
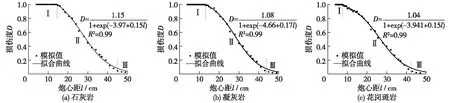
图8 不同岩石损伤D分布规律Fig.8 Distribution law of damage parameter D of different rocks
3 结 语
本文通过模拟石灰岩在不耦合装药下的单孔爆破破坏过程,探究了损伤范围随不耦合装药系数K变化的规律;以石灰岩、凝灰岩和花岗斑岩为研究对象,对比分析了耦合装药条件下岩石爆破损伤在空间上的分布规律,得出以下主要结论:
(1)岩石单孔爆破损伤范围随着不耦合系数增大,压碎区和裂隙区半径与炮孔半径的比值均呈现先快后慢的减小趋势,且裂隙区范围的减小幅度大于压碎区;针对本文工况,当K>2时,炮孔周围岩石几乎不产生压碎区。
(2)不同种类岩石的爆破损伤曲线随炮心距增加均大致呈反“S”形衰减趋势,但损伤分布特征有所差异。石灰岩和凝灰岩因其动态强度较低,故压碎区较大,且与裂隙区过渡界线清晰;而花岗斑岩动态强度较高,其压碎区较小,与裂隙区界线不甚明显。
(3)HJC模型在岩石爆破损伤特征的数值研究中具有较好的适用性。此外,文中计算假定岩石为均质材料,但实际岩石中含随机分布的裂纹等天然缺陷,而且大多处于初始应力状态,因此综合考虑这些因素对爆破损伤的影响尚待进一步研究。
