基于等效单自由度模型的高桩码头地震位移需求分析
2018-11-08高树飞冯云芬贡金鑫
高树飞,冯云芬,贡金鑫
(1. 聊城大学建筑工程学院,山东聊城 252000; 2. 大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024)
基于位移的高桩码头抗震设计方法[1]为美国多本规范和标准[2-5]所采用。该方法要求给出结构在不同设计水准地震下结构的最大位移(位移需求),以及结构在不同材料应变水平下的位移能力,并通过比较位移需求与位移能力验算结构的抗震性能是否满足要求。码头位移需求是惯性作用下上部结构的最大位移反应,在高桩码头抗震计算中,桩-土相互作用的两部分,即惯性作用(与结构质量有关)和运动作用(与岸坡变形有关),是分开考虑的[3,5]。目前确定高桩码头地震位移需求的常用方法有非线性静力需求分析(非线性Pushover分析)方法和非线性时程分析方法。
对于非线性静力需求分析方法,在码头抗震标准中常用的为替代结构法,即用一个等效单自由度体系代替原有结构,等效体系的周期采用割线刚度计算,体系的耗能用等效黏滞阻尼表征[5]。替代结构法由于计算较为简便,在高桩码头抗震计算中得到广泛应用[6]。在替代结构法中,计算结构的等效阻尼比是一个关键步骤,而现行高桩码头抗震设计标准中采用的等效阻尼比公式未考虑土体对体系阻尼的贡献,因而造成按规范公式计算得到的位移需求偏大[7];另外,不同标准采用的等效阻尼比计算公式并不相同,而研究表明[8]等效阻尼比计算公式对确定码头的位移需求有较大影响。此外,替代结构法无法考虑地震动的不确定性。非线性时程分析方法采用逐步积分的方式计算结构的位移反应,充分考虑了结构的弹塑性动力特性和地震动的不确定性,但较为复杂。替代结构法本身就是针对非线性时程分析的复杂性提出的一种简化方法。对于高桩码头的非线性时程分析,桩-土相互作用不可忽视,一般利用非线性Winkler地基上的梁模型进行高桩码头地震反应分析[2-5,9-10],但计算量较大,且较为复杂,易出现不收敛的情况。这种情况在高桩码头易损性分析中变得尤为不利[11-12],因为通常需要采用大量地震动进行时程分析以确定码头的位移需求与地震动强度的统计关系。针对现有高桩码头位移需求评估方法存在的诸多不足,有必要开展研究以寻求一种简便、快捷并具有一定精确度的计算方法。
由于在对工程结构进行非线性时程分析时,原结构通常比较复杂,特别是当计算需要的是结构总体位移而不是构件或截面的地震反应时,故常将结构简化为等效单自由度体系进行分析,这不仅可降低计算难度,且可针对相对较多的地震动记录进行分析,较好地考虑地震动的不确定性[13]。在高桩码头抗震计算中,对于沿码头纵向规则、对称的码头,可以取一个排架及其上部结构按平面问题求解。由于高桩码头上部结构的质量和刚度较大,故可考虑将其简化为单自由度模型。本文建议通过对规则、对称的高桩码头进行单调和往复加载确定结构的恢复力特性(骨架曲线和滞回特性),进而构建等效单自由度模型以代替原码头结构进行非线性时程分析以确定码头的位移需求;同时,以两个典型高桩码头为例,对比利用原型结构和相应的等效单自由度模型分别进行时程分析得到的位移需求,验证本文提出的等效单自由度模型用于确定高桩码头位移需求的合理性和准确性。
1 等效单自由度模型的建立及分析步骤
1.1 高桩码头体系及相应的等效单自由度模型
在高桩码头的水平地震反应分析中,常采用非线性Winkler地基上的梁模型模拟码头结构,如图1(a)所示,土体用土弹簧代替,弹簧一端与桩节点连接,在Pushover(推覆)分析中另一端固定,土弹簧的非线性由p-y曲线模拟,桩的非线性由沿桩身分布的塑性铰模拟。由于高桩码头上部结构的质量和刚度较大,故考虑将其简化为非线性单自由度模型进行地震反应分析,如图1(b)所示。由于码头地震位移需求是惯性作用下上部结构的最大位移反应,故需求分析中可以不考虑岸坡对地震动的影响[5]。
非线性单自由度模型在地震激励下的运动方程为:
(1)
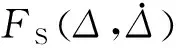
只要将式(1)中的相关动力参数确定即可求解式(1)得到单自由度模型在地震作用下的最大位移,即位移需求。下文将详细介绍相关动力参数的确定方法。对于模型的恢复力,常用方法是对结构进行往复加载以确定其骨架线和滞回特性。

图1 高桩码头分析模型和相应的单自由度模型Fig.1 Analytical model of pile-supported wharf and corresponding single-degree-of-freedom model
1.2 等效单自由度模型的恢复力特性
恢复力特性由骨架曲线和滞回规则构成。由于混凝土桩码头和钢管桩码头的结构特性存在较大差异,故考虑对两种结构分别进行分析以确定其相应的等效单自由度模型的恢复力特性。
1.2.1混凝土桩码头
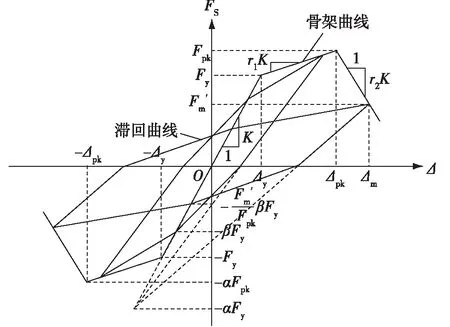
图2 骨架曲线和Pivot滞回模型Fig.2 Backbone curve and Pivot hysteretic model
(1)骨架曲线。文献[5]在Pushover分析中考虑了结构达到最大承载力后的退化,本文亦考虑这一现象。对于混凝土桩码头,建议等效单自由度模型采用如图2所示的三折线骨架线,由弹性段、强化段和软化段组成。骨架曲线由5个参数控制,分别为弹性刚度K、屈服位移Δy、峰值位移Δpk、强化段刚度系数r1和软化段刚度系数r2(r2>0),其中弹性段的刚度为K,参考文献[3]取为Pushover曲线原点到曲线上首个桩塑性铰形成点连线的斜率。当水平位移超过屈服位移Δy后,结构进入强化段,强化段刚度为r1K;在位移Δpk时,结构达到峰值承载力Fpk,随后进入软化段,该段刚度为-r2K。

图3 8根群桩的荷载-变形曲线Fig.3 Load-displacement curve of 8-pile group
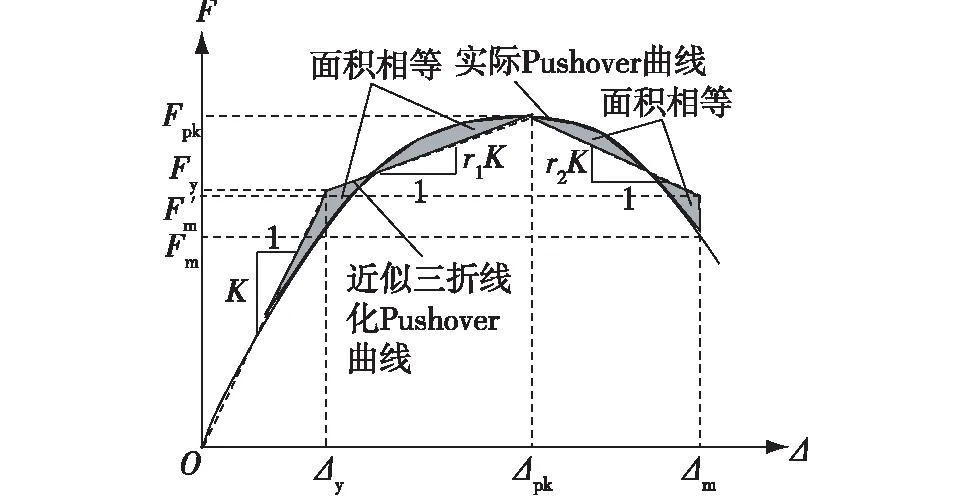
图4 Pushover曲线的折线化Fig.4 Pushover curve linear approximation
一般而言,钢筋混凝土结构在单调荷载下的强度要高于循环荷载下的强度,这也为理论和试验研究所证实[14]。但是在多数情况下,这种由循环荷载引起的强度退化并不显著,可以忽略。图3为Walsh和Ashford[15]对长滩港3号码头进行现场拟静力试验得到的8根群桩(预应力混凝土方桩)的桩顶荷载-位移曲线(1 kip=4.448 kN,1 in=2.54 cm)。由图3不难看出在多个荷载(位移加载)循环下结构的强度退化并不显著,可以忽略,故而建议在这种情况下可通过对单调荷载下的Pushover曲线进行三折线化以得到骨架线,如图4所示,从而简化计算。同时,这可以很好地与码头位移能力的确定结合起来,因为单调荷载下的Pushover分析常被用于确定位移能力。
(2) 滞回规则。确定骨架曲线后,有必要选取一种可以反映码头结构和土体滞回耗能的滞回规则。由图3可以看出,结构卸载刚度随着桩顶位移的增大逐渐减小,反向加载曲线近似与初始加载曲线的弹性段相交于一点,这一现象与图2所示的Pivot滞回模型较为类似,故考虑采用Pivot滞回模型描述混凝土桩码头的滞回特性,图2中α为控制卸载刚度的参数,β为控制滞回环捏拢程度的参数。Pivot滞回模型由Dowell等[16]提出,用于确定钢筋混凝土柱、节点以及框架体系的滞回特性[17],被大型结构分析软件SAP2000所采用。
虽然文献[16-17]给出了钢筋混凝土柱、节点和框架体系的Pivot滞回模型参数(α和β),但显然这些参数不适合高桩码头。为确定适合于高桩码头的Pivot滞回模型参数,文献[18]对典型的全直桩梁板式码头进行低周反复加载数值分析,并在码头建模过程中考虑桩和土体的非线性,得到了式(2)~(5),其中式(2)和(3)适用于灌注桩码头,式(4)和(5)适用于PHC管桩码头;如果码头结构形式和岸坡土体类型与文献[18]中的研究对象相差较大,可参考文献中的方法确定α和β。
灌注桩码头:
(2)
(3)
PHC管桩码头:
(4)
(5)
式中:ρsl为灌注桩中纵筋的配筋率;ρsp为PHC管桩中预应力筋的配筋率;“砂土”指岸坡由砂土组成或岸坡土层中砂土层占多数,“黏土”的含义类似。
1.2.2钢管桩码头
(1)骨架曲线。与混凝土桩码头类似,考虑采用单调荷载下钢管桩码头的Pushover曲线作为其等效单自由度模型的骨架曲线。目前,尚无钢管桩码头低周往复试验研究,文献[18]通过对码头进行数值分析后认为,单调荷载下钢管桩码头的Pushover曲线可用式(6)表示。
(6)

表1 参数a和b的取值Tab.1 Values for parameters a and b
对于黏土,a和b也可分别按式(7)和(8)确定。与混凝土桩码头一样,如果码头的结构形式和岸坡土体类型与文献[18]中的研究对象相差较大,可参考文献中的方法确定相关参数。
a=0.053 7su+1.471 0
(7)
b=-0.005 5su+0.896 3
(8)
式中:Δ1和F1分别为首个桩塑性铰形成时的上部结构水平位移和水平力;a和b为参数,可按表1确定;su为黏土的不排水抗剪强度。

图5 Masing准则Fig.5 Masing rule
(2) 滞回规则。对于钢管桩码头的滞回特性,文献[18]认为码头的滞回曲线可用图5所示的Masing准则[19]进行模拟。
1.3 等效单自由度模型的质量和黏滞阻尼系数
文献[3]和我国《水运工程抗震设计规范》(JTS 146—2012)[20]在计算地震惯性质量时,两者均考虑上部结构质量和上部结构上外荷载的换算质量,但对桩参于振动的质量的处理并不相同,前者取桩顶至坡面以下5倍桩径范围内桩质量的1/3,后者按桩顶的约束条件取全部桩质量的一部分,对于固接取0.37,铰接取0.24。显然如果参照以上标准确定单自由度模型的质量将会得到不同的计算结果,那么将对最终的位移需求产生一定影响。另外上述确定方法只是一种经验方法,并不适用所有工程条件,会带来一定误差。因此建议对建立的考虑桩-土相互作用的高桩码头模型进行振型分析,选取对码头横向反应贡献最大(振型参与系数最大)的振型对应的自振周期T,再根据Pushover曲线原点到曲线上首个桩塑性铰形成点连线的斜率确定的弹性刚度K,按下式确定单自由度体系的质量m:
m=KT2/(4π2)
(9)
得到单自由度体系的质量后,可按下式计算黏滞阻尼系数c:
c=2mωξ
(10)
式中:ω为固有振动圆频率,ω=2π/T;ξ为阻尼比,取5%,这一取值为文献[5]和[20]所采用,本文亦采用该值来考虑码头体系在弹性范围内的黏滞阻尼,而体系在非线性范围内的滞回阻尼则通过体系的滞回模型予以体现。
1.4 分析步骤
综上所述,对于沿码头纵向规则、对称的高桩码头,可以通过将码头简化为单自由度模型进行需求分析,简便计算码头的最大位移,分析步骤如下:
(1)对考虑了竖向荷载的高桩码头施加单调的水平侧向力(位移加载),得到荷载-变形曲线(Pushover曲线)以及首个塑性铰形成时的位移和水平力。
(2)对高桩码头进行往复加载,得到码头的滞回曲线,确定等效单自由度体系的骨架曲线(滞回曲线的包络线)并选择合适的滞回模型,而对于大多数可以忽略循环荷载下强度退化的情况,可直接采用Pushover曲线作为骨架曲线;对于混凝土桩和钢管桩码头,可分别采用Pivot滞回模型和Masing准则模拟码头的滞回特性,相关参数的取值可参考1.2节确定。
(3)对码头进行振型分析,得到等效单自由度模型在弹性范围内的自振周期T,进而确定单自由度模型的质量m和黏滞阻尼系数c,近似计算时也可按照规范的经验方法确定m。
(4)根据得到的骨架曲线、滞回模型、质量和黏滞阻尼系数,按照规范或工程需要选取1组地震动,然后采用相关数值方法(如Newmark-β法)求解式(1),得到单自由度模型的位移反应时程,进而确定最大位移,即可得到高桩码头在设计地震下的位移需求。
2 案例验证
2.1 验证步骤

2.2 案例I

图6 码头断面(单位: mm)Fig.6 Section of wharf (unit: mm)


表2 地震动记录Tab.2 Ground motion records

(续表)编号地震名称台站MWRrup/kmvs/(m·s-1)PGA/g持时/s471999 Chi-Chi, TaiwanCHY088-0007.637.502730.21663.880481999 Chi-Chi, TaiwanTCU079-0007.611.003640.39366.490491999 Chi-Chi, TaiwanCHY036-0907.616.102330.29473.420501999 Chi-Chi, TaiwanCHY101-0907.610.002590.35367.030511987 Whittier NarrowsTarzana, Cedar Hill Nursery A6.041.202570.64438.775521987 Whittier NarrowsGarvey Reservoir Control Building6.014.504680.45725.365531987 Whittier NarrowsLos Angeles, Obregon Park6.015.203490.45038.065541987 Superstition HillsSuperstition Mountain, Site 86.55.603620.68222.130551987 Superstition HillsEl Centro, Parachute Test Site6.51.003490.37722.300561987 Superstition HillsPoe Road-temporary6.511.202080.44622.290571987 Superstition HillsEl Centro, Imperial Co. Center grounds6.518.201920.35839.140581987 Superstition HillsBonds Corner,Hwys 115&986.539.002230.28114.990591987 Superstition HillsWestmorland6.513.001940.21138.580601987 Superstition HillsCalexico Fire Station6.528.902310.21014.990注:表中M4为矩震级,Rrup为断层距, PGA为峰值地面加速度。

图7 灌注桩码头的Pushover 曲线Fig.7 Pushover curves for cast-in-situ pile-supported wharf
由于结构沿纵向对称,取1个排架进行分析。采用非线性Winkler地基上的梁模型模拟码头结构,如图1(a)所示,模型由大型有限元软件SAP2000建立。采用土弹簧模拟桩-土相互作用,并用塑性铰模拟桩的非线性。对码头进行Pushover分析,得到荷载-变形曲线,并按图4对其进行三折线化(如图7),可得到等效单自由度模型的骨架曲线。按式(2)和(3)计算可得α=12.29,β=0.75,由此可确定等效单自由度模型的滞回规则。对码头进行振型分析,得到对码头横向反应贡献最大的振型对应的固有周期T=0.546 9 s。根据Pushover曲线确定的弹性刚度K=5.536 9×104kN/m,由式(9)得m=4.195×105kg,再由式(10)可得c=481.94 kN·s/m。由确定的骨架曲线、滞回模型、质量和黏滞阻尼系数,可建立单自由度动力分析模型。
采用表2中的地震波,分别对单自由度模型和码头体系进行时程分析,得到每条波下单自由度模型和码头最大位移ΔSTHA及ΔNTHA。在对码头进行时程分析时,采用Rayleigh阻尼考虑体系在弹性范围内的阻尼,阻尼比取5%。图8给出了表2中每条地震动下等效单自由度模型和码头的最大位移ΔSTHA和ΔNTHA及其相关系数ρΔ。由图8可知,等效单自由度模型的最大位移与码头的最大位移的相关性较好,接近于1。图9为单自由度模型和码头横梁在编号为28的地震波作用下的位移时程,可见两者的吻合程度较好,说明提出的单自由度模型能够很好地反映码头的动力特性。图10为编号为28的地震波作用下单自由度模型的荷载-变形曲线。图11给出了位移比ΔR的频率直方图以及相应的平均值和变异系数。由图11可以看出,由等效单自由度模型得到的ΔSTHA与码头的ΔNTHA的比值接近于1,且变异系数很小,准确性较好。

图8 案例I的最大位移ΔSTHA和ΔNTHAFig.8 Maximum displacements ΔSTHAandΔNTHAfor case study I
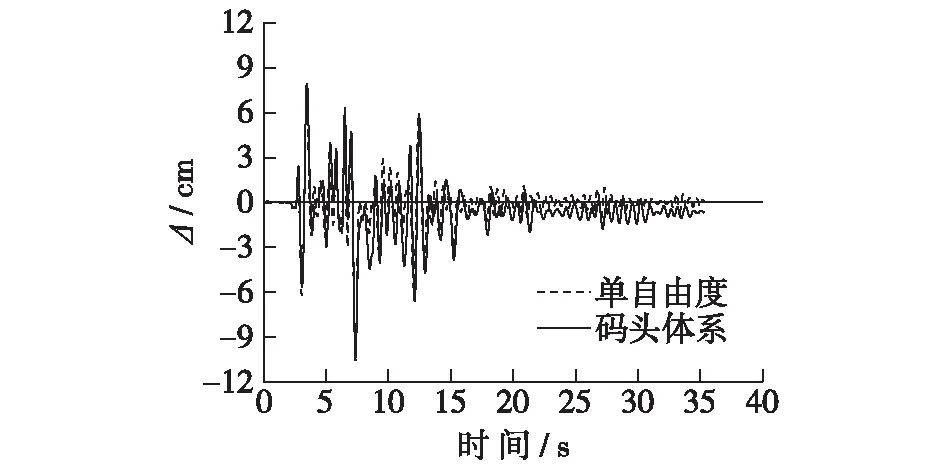
图9 单自由度模型和码头位移反应Fig.9 Displacement response of SDOF model and wharf

图10 单自由度模型的荷载-变形曲线Fig.10 Load-deformation curves of SDOF model

图11 案例I位移比ΔR的频率直方图Fig.11 Frequency histograms for displacement ratio ΔR of case study I
2.3 案例II
码头断面仍采用图6所示的断面图,但桩采用直径800 mm的钢管桩,壁厚10 mm,钢管桩采用Q345钢材。岸坡土体类型为砂土,砂土内摩擦角为30°。对高桩码头进行Pushover分析,得到荷载变形曲线。并按式(6)确定近似的Pushover曲线,如图12所示,可得到等效单自由度模型的骨架曲线,模型的滞回特性采用Masing准则模拟。对高桩码头进行振型分析,得到对码头横向反应贡献最大的振型对应的固有周期T=0.758 0 s。根据Pushover曲线确定的弹性刚度K=2.360 3×104kN/m,由式(9)得m=3.435×105kg,再由式(10)可得c=284.75 kN·s/m。由确定的骨架曲线、滞回模型、质量和黏滞阻尼系数,可建立单自由度动力分析模型。
仍然采用表2中的地震动,分别对单自由度模型和码头体系进行时程分析,得到每条地震波下单自由度模型和码头的最大位移ΔSTHA及ΔNTHA。在对码头体系进行时程分析时,采用Rayleigh阻尼考虑体系在弹性范围内的阻尼,阻尼比取5%。图13给出了表2中每条地震动下等效单自由度模型和码头的最大位移ΔSTHA和ΔNTHA及其相关系数ρΔ;可以看出,ΔSTHA和ΔNTHA的相关性较好。图14为单自由度模型和码头横梁在编号为28的地震波作用下的位移时程;可以看出两者的吻合程度较好,说明提出的等效单自由度模型能很好地反映了钢管桩码头的动力特性。图15为编号为28的地震波作用下单自由度模型的荷载-变形曲线。图16给出了位移比ΔR的频率直方图以及相应的平均值和变异系数。由图16可以看出,由等效单自由度模型得到的ΔSTHA与码头的ΔNTHA的比值接近于1,且变异系数很小,准确性很好。

图12 钢管桩码头的Pushover 曲线Fig.12 Pushover curve for steel

图13 案例II的最大位移ΔSTHA和ΔNTHAFig.13 Maximum displacements ΔSTHA and ΔNTHAfor case study II

图14 单自由度模型和码头的位移反应Fig.14 Displacement response of SDOF model and wharf
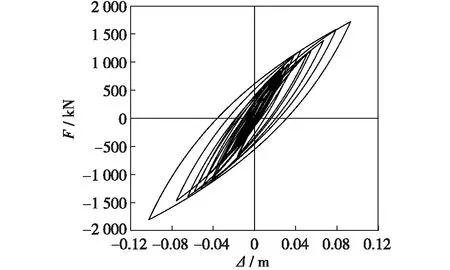
图15 单自由度模型的荷载-变形曲线Fig.15 Load-deformation curves of SDOF model

图16 案例II位移比ΔR的频率直方图Fig.16 Frequency histogram for displacement ratio ΔR of case study II
3 结 语
针对现有高桩码头位移需求计算方法存在的不足,提出一种可用于时程分析的单自由度模型。该模型通过对码头进行单调和往复加载分析后得到,并通过两个高桩码头案例验证了其合理性和准确性。该模型可适用于沿纵向对称、规则的码头。经过研究分析得出以下结论:
(1)将原码头结构等效为单自由度模型,使得多自由度体系的位移反应计算简化为对单自由度体系的求解,不仅大大提高了计算效率,而且计算结果具有足够高的精度,特别适用于需要采用大量地震动记录的情况,如码头的易损性分析。
(2)对于大多数情况而言,循环荷载引起的码头结构强度退化可以近似忽略,采用单调荷载下的Pushover曲线可以反映码头的承载能力。
(3)Pivot滞回模型可以很好地模拟混凝土桩码头的滞回特性,该模型的参数较少且易于确定,并具有很强的适应性;采用Masing准则模拟钢管桩码头的滞回特性是可行的,利用单一的公式可以描述钢管桩码头的Pushover曲线。
(4)码头上部结构的位移时程与等效单自由度模型的位移时程有较强的相似性,进一步说明了将码头简化为单自由度模型进行地震反应分析的合理性。
