磷酸铁锂电池内阻连续动态测量与分析*

2018-11-07陈明彪林仕立宋文吉冯自平蒋海洲

新能源进展 2018年5期

李扬，陈明彪，林仕立，宋文吉†，冯自平，蒋海洲

（1. 中国科学院广州能源研究所，广州 510640；2. 中国科学院可再生能源重点实验室，广州 510640；3. 广东省新能源和可再生能源研究开发与应用重点实验室，广州 510640；4. 中国科学院大学，北京 100049；5. 中国电子科技集团公司第二十二研究所，山东青岛 226107）

0 引言

磷酸铁锂电池的性能与电池温度有关，温度会影响电池的内阻[1-3]、容量[2-5]、能量[2,4]、倍率性能[4]、循环效率[2,4,6]、循环寿命[4,6-9]和安全性[4,6,10]等。其中，内阻大小变化最为直观，可通过内阻变化表征电池其他特性的变化。不同荷电状态（state of charge,SoC）下内阻不同[11-13]，利用内阻与 SoC之间的关系，测出内阻即可预测电池的荷电状态[12-13]；电池老化会导致电池性能发生变化，内阻的改变是衡量老化的一项重要指标[14-15]。通过电池容量衰减与内阻增长的关系，测出内阻便可预测电池的老化程度，这对电池的梯次利用及提高电池安全性具有重要意义[16-17]；内阻和电池温度之间也存在变化关系，通过内阻测量可以表征电池内部的温度特性[18]，与传统电池内置温度传感器的测量手段[19-21]相比，既经济又安全。对电池组而言，内阻匹配尤为重要，失配会导致并联电池间电流不均衡，加剧电池包老化[6,22]。若不控制不均衡趋势[23]，将会导致热失控[7,24]。因此，了解电池内阻、容量、能量在不同温度下的变化规律，对电池的使用和管理具有重要意义[25]。

电池内阻测量目前多采用脉冲法[26]、混合脉冲充放电（hybrid pulse power characterization, HPPC）法[27]。受弛豫效应影响，测试时间较长且测量结果非连续，在后期数据处理过程还会因人为选点因素导致计算结果出现偏差。因此，本文提出了一种测量内阻的方法——双倍率曲线法，利用一大一小两股不同倍率曲线，便捷、高效地测出连续的内阻[28]。

双倍率曲线法测量内阻能够大大减少测量时间。CHEN等[26]采用脉冲法测量内阻，选取10个测量点，分别对应不同的 SoC，每个测量点测量时长50 min，总耗时8 h。如需增加测量点，耗时更长。相比而言，双倍率曲线法仅需测量一次小倍率放电曲线，待要测量某一电流倍率放电时的内阻，只需让其恒流放电即可。如测量C/4，耗时4 h，且测量结果连续而非离散，可以认为其测量点无穷多。该方法的提出能够有效地缩短内阻测量时耗，并对在线内阻测量的实现提供了一定的研究基础。

1 试验原理与方法

1.1 试验原理

电池内阻Rtot包括欧姆内阻Ro和极化内阻Rp，其中极化内阻受温度与电流密度影响较大，而欧姆内阻大小基本不变[1-2]。根据欧姆定律得：

式中，In为待测内阻对应的放电电流；Imin为小倍率放电电流（亦称参比电流）；T为电池温度；Uocv为开路电势；U为负载电压。联立（2）、（3）两式得：

理论上，参比电流Imin越小越精确，考虑试验周期及仪器精度的影响，参比电流不宜过小。因此，权衡以上因素，本文选用C/25作为参比电流。

1.2 试验方法

本次试验以 3.2V/20A·h磷酸铁锂/石墨软包电池为研究对象，利用BPH-120A恒温箱改变环境温度，采用LAND-CT 2001B充放电仪调控充放电制度，通过Agilent 34972A数据采集器得到不同温度下两条不同倍率的放电曲线。具体试验步骤如下：

（1）将电池置于25℃恒温箱中，静置2 h，待电池达到热平衡后以6 A恒流充电至截止电压3.65 V，当充电电流小于1 A（C/20）时结束充电。

（2）重新设定恒温箱温度（从60℃ ～ −15℃，间隔15℃）。将电池置于恒温箱，静置2 h后以C/25倍率恒流放电至截止电压2.7 V，并记录电压数据。

（3）改变步骤（2）中放电倍率为C/4，重复步骤（1）、（2）。

（4）改变步骤（2）中恒温箱温度，重复步骤（1）、（2）、（3）。

2 试验结果与讨论

2.1 温度对内阻的影响

2.1.1 电池产热对温度的影响

锂离子电池在充放电过程中会释放热量。对等温电池而言，产热速率[29]按下式计算：

根据式（6）可知产热率q与电流I成正相关，即电流越小产热率越小。此外电池内部温度场不均匀也会改变内阻，不均匀温度场下的内阻特性与对应平均温度下均匀温度场的内阻特性相近[28]。本文采用C/4倍率放电，试验中通过热电偶采集到的电池表面各部分温升均不超过 1℃，故可忽略电池产热对温度的影响。每次放电前都会将电池在恒温箱中静置2 h，足以使电池在放电之前达到热平衡。综上，可认为放电过程中的电池温度等于环境温度。2.1.2 测量方法的适用性分析

本次试验分别在6组不同温度下进行，得到了6组双倍率放电电压曲线。通过对每组数据进行电压比容量（dV/dQ）处理，得到了不同温度、不同倍率下的dV/dQ曲线如图1。在放电过程中有一大段区域电压变化较缓。在5% ～ 90%放电状态（state of discharge, SoD）段，−15 ～ 60℃温度区间的电压变化很小。不同温度和 SoD区间的平均电压比容量dV/dQavg如表1所示。

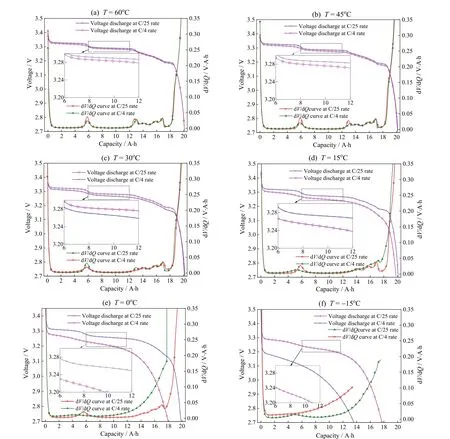
图1 不同电池温度C/25、C/4放电条件下，dV/dQ和电压与放电容量变化关系Fig. 1 dV/dQ and voltage vs. capacity for a lithium-ion battery discharging at C/25 and C/4 rate

表1 C/4及C/25放电倍率下，不同温度、不同SoD区间的平均电压比容量Table 1 Value of dV/dQavg at different SoD intervals with different temperatures at C/4 and C/25 rate

对比发现，不同放电倍率下 dV/dQ值相差不大，且在平稳段（5% ～ 90%SoD）内dV/dQavg的值远小于开始段（0% ～ 5%SoD）和末尾段（90% ～100%SoD）。故从误差分析的角度考虑，开始段与末尾段误差过大（2.2.2小节将对误差做具体分析），舍去。在高温段（30 ～ 60℃），C/25放电条件下的dV/dQavg.(5%～90%SoD)大小基本不变；而当放电倍率提高到C/4时，维持dV/dQavg.(5%～90%SoD)大小不变的温度下限将提高，即维持dV/dQavg.(5%～90%SoD)大小恒定的温度区间变窄，为 45 ～ 60℃；低温段（−15 ～ 30℃）在C/25与C/4倍率放电条件下，dV/dQavg.(5%～90%SoD)大小均随环境温度降低而急剧增大，且放电倍率越大受温度影响越显著，温度区间也越宽。这一现象与放电容量随温度、放电倍率变化规律相似。对比图2中C/25、C/4两条曲线，可以很好地观察到这一变化规律。

图2 dV/dQavg.与温度之间关系Fig. 2 Average of dV/dQ vs. temperature for a lithium-ion battery discharging at C/25 and C/4 rate

此外，如图2右半侧所示，两种倍率放电下低温段 dV/dQavg.(5%～90%SoD)的自然对数值与温度的倒数呈正相关。用函数y= ax+ b对低温段进行线性拟合，得到C/25、C/4拟合曲线方程如式（7）和式（8）：

拟合优度分别为R2= 0.88448和R2= 0.97697，拟合模型与实际模型比较吻合。比较式（7）和式（8）发现拟合曲线满足Arrhenius 公式lnk= −Ea/RgT+lnA，且两式斜率a大小基本相同，由图2也可看出两条直线近乎平行。因此，两条曲线的不同是由截距 lnA的不同造成，即倍率放电的不同仅造成指前因子A的差异，而不对其他因素造成改变。这一结论很好满足Arrhenius公式。对同一电池而言，活化能Ea和摩尔气体常数Rg大小均为常数，故斜率不随电流大小改变。

2.1.3 温度对内阻的影响

根据上述分析可知，双倍率曲线法测内阻适用于SoD在5% ～ 90%内，超出这一范围，测量精度较低。通过式（5），计算得到电池在不同温度下C/4放电倍率的内阻。

图3 不同温度下内阻随放电容量的变化Fig. 3 Internal resistance varies with discharge capacity at different temperatures

图3给出了不同温度下内阻与容量之间的关系，从图中可以看出，内阻的计算结果在放电开始段与末尾段存在明显的误差，甚至出现内阻为负数的情况。因此，重新绘制内阻与SoD之间的关系图，截取横坐标在5% ～ 90%SoD段，如图4所示。

可以看出，当放电倍率一定时，电池内阻随温度的降低而增大。由图4还可以发现，环境温度较高时，放电过程中不同SoD对应的内阻大小几乎保持不变；而当温度较低时，随着放电过程的持续进行，内阻呈增长趋势，且在SoD较低时，内阻增速缓慢，几乎不变，当SoD较高，内阻增长速率急剧上升。推断电阻随温度降低而升高是由于电池极化内阻的增大。离子的扩散速率与温度成正相关，当温度降低，电池内锂离子扩散速率降低，导致锂离子在正负极的脱嵌过程受阻，增加了极化内阻，进而导致总内阻增加[2]。而低温下电池内阻随放电时间延长而急剧增大，是由于脱嵌过程的不断受阻，导致极化内阻持续增大，宏观表现为电池总内阻持续增大。

图4 不同温度下内阻随SoD变化图Fig. 4 Internal resistance varies with SoD at different temperatures

2.1.4 内阻与温度之间的关系

选取6组试验数据里5% ～ 90%SoD段的内阻，求出不同温度下对应内阻的算术平均值Ravg（表2）。

表2 5% ～ 90%SoD段C/4倍率条件下不同温度对应的平均内阻Table 2 Average resistance (Ravg) at different temperatures under conditions of 5% ～ 90%SoD and C/4

将得到的不同温度下电池的平均内阻取对数ln(Ravg)，与温度的倒数1/T进行作图处理（图5），处理后发现ln(Ravg)与1/T呈线性相关。

图5 内阻与温度的变化关系Fig. 5 Relationship between internal resistance and temperature

对相关数据采用一次函数y= ax+ b线性拟合，得到拟合函数如式（9），其中拟合优度R2= 0.9831。

变换得到平均内阻Ravg与温度T的关系式：

2.2 误差分析

本次试验误差来自于测量误差（measuring error）与试验理论误差（theoretical error）两个方面，其中测量误差由仪器误差（instrumental error）和操作误差（operation error）组成。

2.2.1 仪器误差分析

仪器误差来自于测量仪器本身不够精密所造成的测定结果与实际结果之间的偏差。本次试验恒流放电采用LAND-CT2001B（量程10 A）充放电仪，精度为0.1%RD ± 0.1%FS，电压的测量采用Agilent 34972A（量程10 V）数据采集仪，精度0.002%RD ±0.0005%FS。相对误差ε大小按下式计算：

将式（5）代入得仪器精度误差εins计算式为：

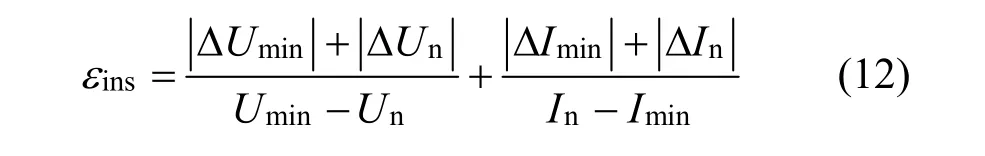
式中，ΔUmin为参比电流C/25下电压的仪器绝对误差；ΔUn为待测电流C/4下电压的仪器绝对误差；ΔImin为参比电流C/25下电流的仪器绝对误差；ΔIn为待测电流C/4下电流的仪器绝对误差。对于本次试验而言，式（12）中第三项、第四项为常数，其和为 (0.1% × 0.8 + 0.1% × 10)/(5 − 0.8) + (0.1% × 5 +0.1% × 10)/(5 − 0.8) = 0.6143%，对于不同温度、不同放电时刻Umin、ΔUmin、Un、ΔUn均不一样，因此第一项、第二项为温度与时间的变量，即εins大小在不同温度和不同放电时刻是变化的。据此，分别考虑不同温度下 5% ～ 90%SoD段的最大仪器误差（εins.,max）、最小仪器误差（εins.,min）、平均仪器误差（εins.,mean）如表3。

从表3中可以看出，仪器误差随温度的降低而减小，且仪器误差的变化是由于式（12）中电压项决定，仅和数据采集器精度有关。当电池温度较高时，仪器误差主要受数据采集器精度影响；而电池温度较低时，仪器误差主要受充放电仪精度影响。

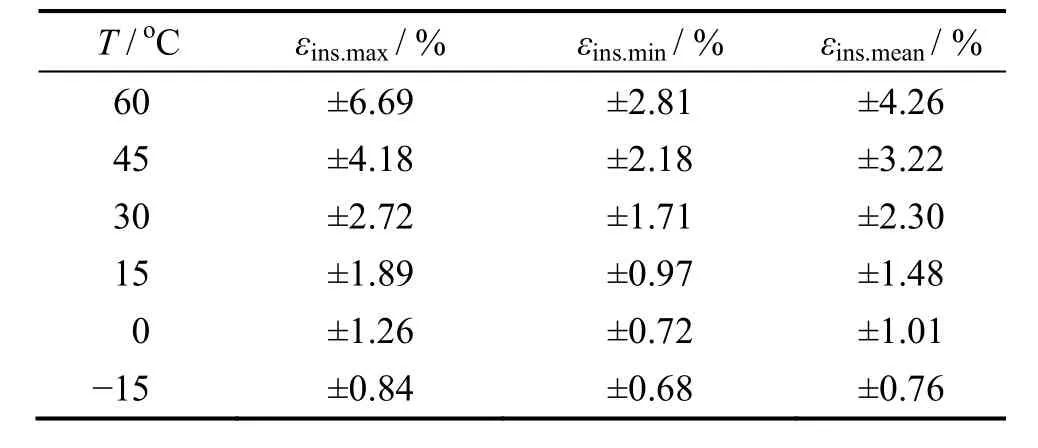
表3 5% ～ 90%SoD段不同温度下的仪器相对误差Table 3 Instrument relative error at different temperatures with SoD of 5% ～ 90%

2.2.2 操作误差分析

操作误差是由于测量步骤的不尽完善引起的测量结果误差。本次试验每隔20 s记录一次试验数据，由于充放电仪与数据采集器分别独立运行，因此两种倍率曲线的放电时间最大可能错位40 s。可假定C/25的数据记录比实际提前20 s，C/4比实际滞后20 s。时间上的错位导致了放电状态的错位，进而影响两股电压曲线相对位移，导致式（5）中的U(Imin,T) −U(In,T)值被放大或缩小。由式（11）得到操作相对误差为：

式中，ΔQmin为参比电流 C/25下容量的位移，ΔQn为待测电流C/4下容量的位移，(dV/dQ)min为参比电流C/25下电压比容量，(dV/dQ)n为待测电流C/4下电压比容量。根据：

分别得到ΔQmin和ΔQn的值。由图1知， dV/dQ与SoD有关，因此式（13）中的εope也随SoD变化，为能更好地反映不同SoD区间里整体的误差大小，宜选用平均电压比容量dV/dQavg。表1给出了不同温度和SoD区间的dV/dQavg，带入式（13），得到操作平均相对误差εope如表4。由表4可以看出，在开始段（0% ～ 5%SoD）和末尾段（90% ～ 100%SoD）操作平均相对误差过大，舍去，这印证了2.1.2小节中的分析。而开始段、末尾段平均相对误差大小不等，则由于选取的SoD区间过于粗略导致。虽然表4中给出了相对误差大小随着温度降低而减小，但绝对误差δope却随着温度降低而增大，根据绝对误差计算公式：

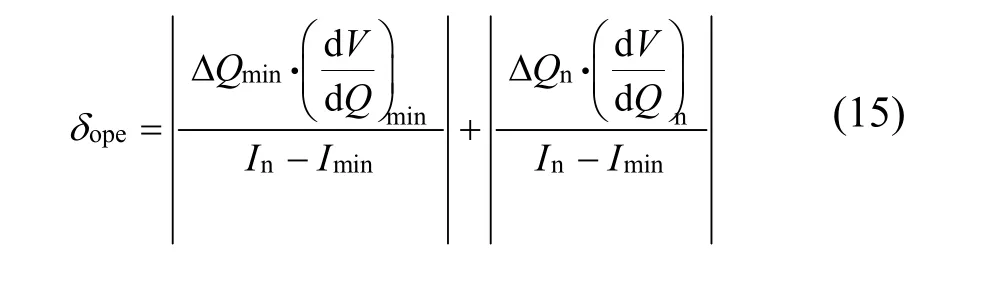
表4 不同温度下各SoD区间内操作误差的平均值Table 4 Average of operation relative error with different temperatures

由表1知(dV/dQavg)min和(dV/dQavg)n随温度的降低而增大，即绝对误差随温度降低而增大。

对于操作误差，可通过增大采样频率来降低，或采用两种不同采样频率分别采样，使得不同倍率的采样数据对应的放电容量一致等途径来降低误差。

2.2.3 理论误差分析

本次试验理论误差εthe来自于对式（4）最后一项的舍去。当参比电流趋近于 0时，该项为 0，但通过 1.1小节的分析知参比电流不宜过小。本次试验中取C/25，观察式（4）可知，舍去最后一项后的测量值比真实值偏大。将式（4）变形得：

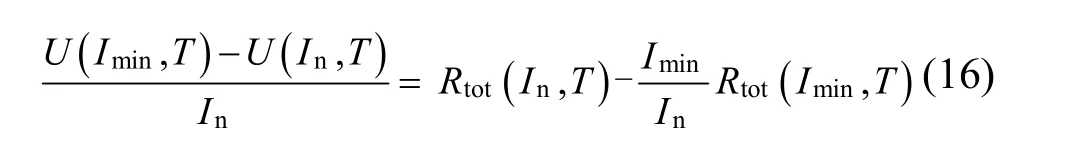
观察式（16）可知，舍去最后一项后的测量值比真实值小。据此，可以得出真实值R的范围为：

通过式（17），得本次试验最大试验理论误差为：

计算结果偏大，故符号为“+”。理论误差εthe大小仅和放电倍率有关，而与温度无关。当待测电流与参比电流差值越大，试验理论误差越小。定量分析得：待测电流的倍率每增大一倍，实验理论误差大小就减小为原来的1/2；参比电流缩小一倍，实验理论误差也减小为原来的1/2。但参比电流减小值下限受仪器自身限制，且放电倍率过小时，放电时间太长。

本次试验总误差大小等于各部分误差代数和，通过上述分析，得出不同温度下总误差如表5。

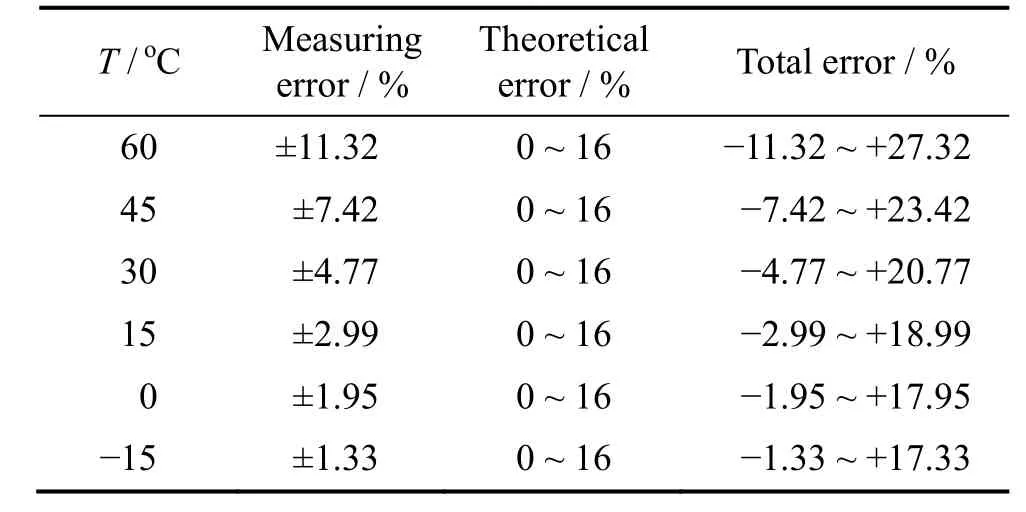
表5 5% ～ 90%SoD段不同温度下的总误差Table 5 Total error at different temperatures with SoD of 5% ～ 90%

可以看出，最大误差随温度降低而减小，总体而言实验精度满足工程需要，其中理论误差大小占主导地位，为+16%。由之前叙述知仪器误差和操作误差与温度及电流倍率有关，理论误差仅同电流倍率有关。在不考虑电流增大对电池温升影响的情况下，当待测电流的倍率每增大一倍，实验理论误差大小就减小为原来的1/2。因此提高待测电流倍率，将显著提高测量精度。

粗略估计，当放电倍率为1 C时，30℃时内阻测量的总误差范围为 −2% ～ 5%，且随着测量仪器精度的提高，取样频率的增大，测量误差还有望进一步降低。这对在线测量内阻有着重要意义。