太阳位置算法的计算误差对辐射预测的影响*

鲍鹤鸣，顾一凡，刘 超，高淑宁，关 欣

（上海理工大学能源与动力工程学院，上海 200093）

0 引 言

随着人来对能源需求量的增大，传统能源储备量逐渐减少，以太阳能为主的新能源正推动着全球能源系统的转变。根据国际能源署（International Energy Agency, IEA）《2017世界能源展望》统计，光伏发电的装机容量正以空前的速度增长，预计至2040年，太阳能将成为最大的低碳发电能源[1]。预测太阳能系统的输出功率对太阳能系统最佳能量管理至关重要。然而，在预测太阳能系统输出之前的预测重点则是太阳能辐照度[2]。通常，太阳辐射量可从气象监测站点获得，但监测站点的太阳辐射量不能准确地反映出太阳能系统工作区域的太阳辐射能量，因此对不同地区工作面进行准确太阳辐射量的研究，具有重要的理论和实际意义[3]。经历半个多世纪的发展，散射辐射模型得到了不断完善，辐射模型的计算精确度不断提高[4]。典型的太阳辐射计算模型有假设各向同性的Liu and Jordan模型[5]，基于各向同性漫辐射的Bugler模型[6]，以及目前广泛使用的 Perez各向异性模型，该模型将散射辐射划分为环日辐射、水平面亮度散射、穹顶散射三个部分[7-8]。在提高辐射计算模型计算精度方面，国内外学者也进行了大量研究，但大多只注意散射模型的优化，往往忽略了太阳位置算法精确度对太阳辐射计算的影响。吴贞龙等[4]和邓艳君等[9]在对辐射的研究中忽略了太阳位置算法误差所带来的影响。王志敏等[10]和武晓伟等[11]在其辐射模拟计算研究中均采用柯伯方程计算太阳赤纬角，未考虑地球轨迹的变化对辐射计算造成的影响。曾理等[12]在计算太阳辐射时，对海拔高度和大气层外水平辐射太阳光入射角均进行了优化，但是在偏心修正系数和太阳赤纬的优化中却采用了柯伯方程，忽略了地球轨迹变化的影响。在神经元网络等对太阳辐射预测的方法中[13-14]，普遍采用的是晴空系数或时变系数的方法，消除太阳位置变化对太阳辐照值的影响和降低日出和日落之间过渡点的预测误差，而这两种方法均需要获取准确的太阳方位参数。美国国家可再生能源实验室（National Renewable Energy Laboratory,NREL）曾提出，入射角计算结果0.01°的误差会在太阳天顶角 80°以上计算中造成至少 1%的计算误差[15]，由此可见，太阳位置算法的精确程度对太阳辐射计算会产生不可忽略的影响。

由于所有的辐射模型计算中均需要采用大气层外水平面辐射值，因此，本文以大气层外水平面辐射值为分析对象。为保证分析结果的准确性，以紫金山天文台公布的《中国天文年历》数据为太阳位置参数基准，分别以太阳赤纬角和日地距离对辐射的影响程度进行分析，并与两种高精度太阳方位算法进行了对比研究。

1 研究方法

目前，太阳追踪装置中广为采用的太阳位置算法可分为从天文年历中提取变量并采用傅里叶变换回归的数值模拟法和根据纽康（太阳表）中所列的理论展开式简化后直接计算两种方式[16]。然而辐射计算中太阳位置参数的计算大多采用柯伯方程，鲜有采用 Bourges等数值模拟法，理论展开式的计算方法更是寥寥无几。大气层外水平面太阳辐照度的计算式是辐射计算研究的基础，其不受大气蒙气差等因素的影响，能够直接反映出太阳方位参数误差对辐射计算的影响。本文以大气层外水平面太阳辐照度的计算误差为研究对象，计算式如下：

式中，GSC为太阳常数值，GSC=（13 6 7 ± 7 ） W / m2；Go,n射角的 c osθZ值以及地球运行轨道偏心修正系数两个方面分析其对辐射计算的影响。为一年中第n天在法向平面上测得的大气层外的太阳辐照度；ξo为偏心修正系数；θZ为太阳入射角。

如式（1）所示，计算大气层外水平面太阳辐照度时需要两个太阳方位参数，即地球运行轨道偏心修正系数和太阳入射角。因此，本文分别从太阳入

2 太阳方位参数计算误差对辐射计算的影响

2.1 入射角计算误差对辐射计算影响

大气层外水平面辐射的计算中太阳入射角是主要影响其计算精确度的太阳方位参数之一。c o sθZ的计算受赤纬角和时角的共同影响，根据几何关系，cosθZ表现形式如下：

式中，δ为太阳赤纬角；φ为当地纬度；ω为时角。

柯伯方程是在太阳辐射计算中被广为采用的太阳方位参数算法。然而柯伯方程每一年中每一天的太阳赤纬为一个恒定不变的数值。一方面由于各年际间参数都存在一定的差异，柯伯方程使用单一值去满足各年的变化不可避免地会出现偏差；另一方面，地球绕太阳运行轨迹并不是规则的椭圆，也会产生较大的偏差。依照柯伯方程，太阳赤纬δ可由下式概算：

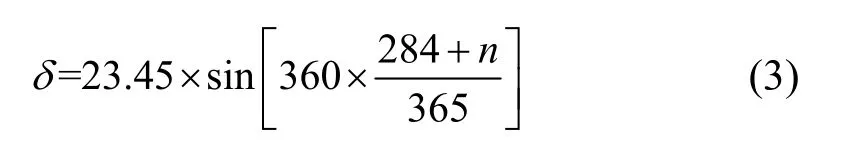
式中，n为积日，例如，春分为n= 81。

设太阳赤纬误差引起的 c osθZ太阳入射角计算的相对误差为εθ,n，其表达式为：

式中，θδ,n为以一年中第n天天文年历的太阳赤纬值计算的太阳入射角；θδ',n为以一年中第n天柯伯方程计算的太阳赤纬值计算的太阳入射角。

图1为柯伯方程计算的2015年赤纬角值与标准值的绝对误差，为了使分析结果准确，以紫金山天文台地理经纬度坐标为观测点坐标，以柯伯方程计算2015年赤纬角值的绝对误差，两个误差极值分别发生在第62天和第284天，误差度数分别为0.504 5°和1.290 5°。为了准确得到赤纬角计算的误差对太阳入射角余弦值计算结果带来的误差影响，只改变赤纬角值，以 10°为步长分别计算时角ω =0° ～ 90°下的值（剔除了计算的太阳入射角小于零的值）。图2为不同时角下太阳赤纬角计算误差对计算结果的影响规律。由于太阳入射角的计算误差与赤纬角计算误差成正相关关系，图2所示的误差峰值与图1中赤纬角计算绝对误差峰值出现的日期一致，而且随时角的增大而增大。

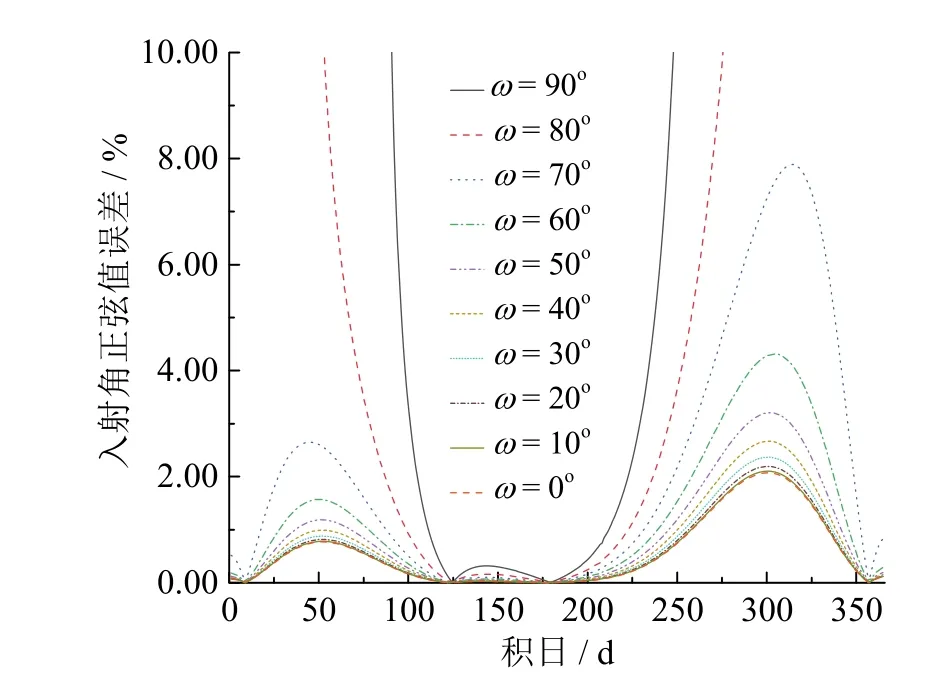
图2 不同时角赤纬角误差造成 c osθZ计算的相对误差Fig. 2 Relative error of cosθZ calculation due to the decentration angle error at different time angles

表1列出了各时角下 c osθZ计算误差极值，在ω= 0° ～ 40°范围内，赤纬计算误差对 c osθZ计算误差的影响程度相近，该范围内全年平均相对误差为0.67%，平均最大峰值为2.44%。当ω＞ 40°时，赤纬计算误差引起的 c osθZ计算误差影响程度明显加剧，70°时最大误差峰值达到7.89%。尽管剔除了以天文年历参数为基础计算入射角θZ在时角为80°和90°时的计算负值，但在近日出日落时角的区域仍出现异常的极大误差。

表1 不同时角下 c osθZ值的相对误差峰值Table 1 Relative error peaks of the values of c osθZ at different time angles

表2为异常误差处的太阳入射角计算结果，引起图2和表1中极大误差的原因是由于赤纬角计算误差使得年历参数计算入射角值为正值，而柯伯方程计算为负值。需要说明的是，当计算太阳高度角α≤0°则没有辐射，使所有太阳高度角小于零的cosθZ值为零，因此 c osθZ的计算误差就修正为100%。由此可见，这样的异常极大误差普遍存在于太阳高度角为零的计算区域，对辐射计算会造成极大干扰。

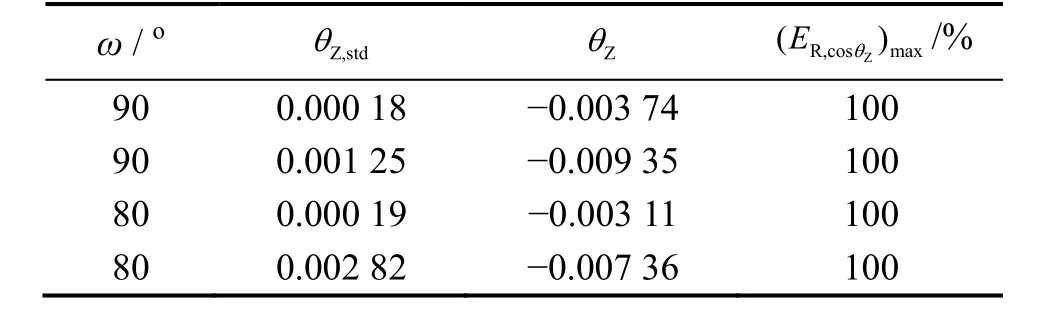
表2 异常误差处太阳入射角计算值Table 2 Calculated value of solar incident angle at anomaly error

由式（1）可知，大气层外水平面辐照度与 c osθZ值成正比例关系，因此辐照度误差分析表达式如下：

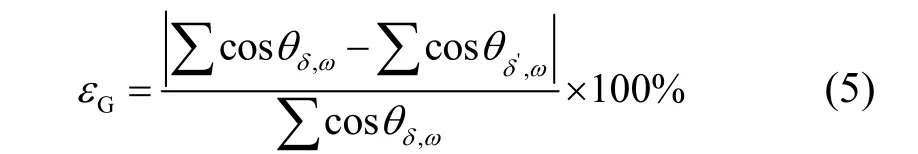
式中，εG为辐照度误差，δ为天文年历参数计算的太阳赤纬角，δ’为方程计算的太阳赤纬角。

为了进一步明确太阳方位参数计算的误差给辐射计算带来的误差影响程度。剔除临界点的极大误差值，使得所有计算值均有意义，忽略日地距离变化，即ξo取常数1，计算出每一天中日出日落时的时角，分别向前向后各取时角1°（4 min）为步长，计算每一天的辐射量。一年中日平均辐射的计算误差结果如图3所示，误差峰值与赤纬计算误差峰值在相近的时间出现两次极值，最大误差极值2.97%，年平均计算误差 1.01%。值得说明的是该计算结果是在忽略了临界点极大误差情况下得出的，若不剔除极大误差点则会造成更大的计算误差。

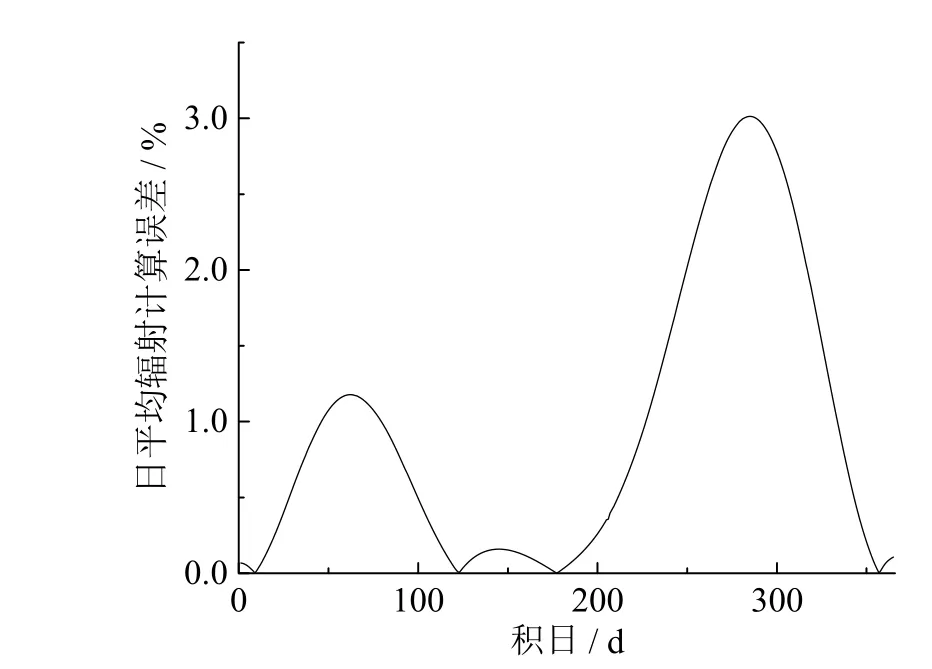
图3 一年中日平均辐射计算误差Fig. 3 Annual average radiation calculation error

2.2 偏心修正系数误差对辐射计算的影响

由于地球绕太阳运行的轨道是偏心率很小的椭圆形轨道，日地距离有近日点与远日点之分。偏心修正系数用于修正太阳辐射随地球运行轨道变化，常采用如下简化公式：

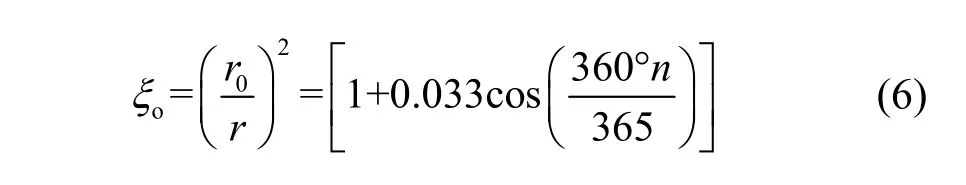
式中，r0为平均日地距离，为1个天文单位（149 597 870 km）；r为观察点的日地距离。

偏心修正系数简化计算公式存在与柯伯方程类似的问题，单一值去满足各年的变化不可避免地会出现偏差。与上节采用同样的方法，只改变偏心修正系数，固定其他参数，考察偏心距离修正公式对辐射计算的影响。设偏心修正引起的误差为εξ，其表达式为：

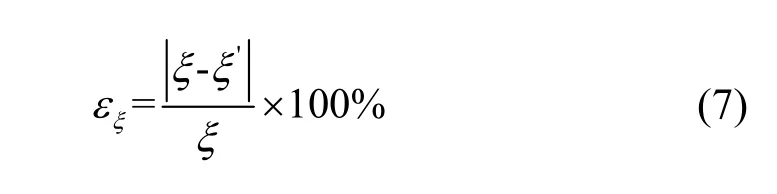
如图4所示，偏心修正系数误差与赤纬计算误差对辐射计算误差的趋势基本一致，且两个极值点发生时间类似，尽管偏心修正对太阳辐射计算影响仅在0.3%以内，但是两种误差发生时间一致，因此很有可能造成误差重叠，扩大辐射计算的误差。

图4 偏心修正误差对日平均辐射的计算误差Fig. 4 Calculation error of daily radiation corrected by eccentricity correction error

2.3 太阳方位参数误差复合影响

由于赤纬计算误差与偏心修正对日辐射计算造成影响随积日变化规律一致，两方面的计算误差会对辐射计算造成复合影响。图5为两参数复合计算的辐射误差结果，地球运行轨迹的偏心修正消除了柯伯方程赤纬计算的极大误差值，但却整体增大了全年每日的平均辐射计算误差，使得全年日平均辐射量计算误差平均为1.05%左右。尽管1%的辐射计算误差在部分工程应用中可以忽略，但这样的误差在太阳辐射计算、测定等领域不容忽视，更重要的是方位参数误差造成计算误差与非均质大气影响带来的计算误差不同，太阳方位参数造成的计算误差是可以通过更精确的太阳方位算法优化消除。

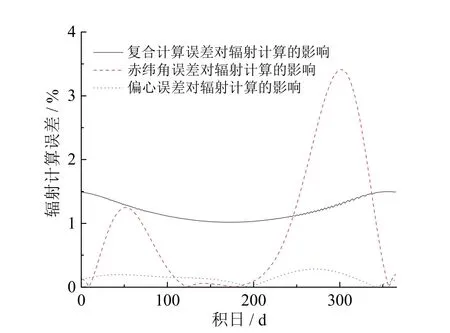
图5 两参数对辐射计算误差的复合影响图Fig. 5 Composite effect of two parameters on radiation calculation error

表3 本文与文献[9]中辐射计算误差随时间变化规律对比Table 3 The variation of radiation calculation error with time comparison of this paper and reference [9]

表3列出了文献[9]在2001年1月15日、4月15日、7月15日、10月15日辐射计算的部分结果，忽略了太阳方位算法的影响，但辐射计算误差结果的变化趋势与本文分析结果的变化规律相似。这也证明太阳方位算法的误差对大气层外水平面辐射的计算影响随大气层外水平面辐射传递至辐射计算，对辐射计算结果造成累积误差。然而辐射计算模型中的累积误差完全可以通过更精确的方位参数计算方程减小甚至消除。

3 高精度的太阳方位算法的应用

3.1 太阳赤纬拟合公式的改进

太阳方位的计算误差会随大气层外辐射的应用对辐射计算方程产生影响，影响辐射计算模型的准确性，而太阳方位参数的误差造成的影响可以通过高精度的算法修正。以往的数值模拟算法自变量均取自积日，最小单位为日，为了能够精确地反应出不同时刻内的赤纬计算精度，引入儒略历元作为自变量改进计算方法。改进后计算方法如下：

天文年历从 1984年起采用儒略历元代替贝塞尔历元，自1994年国际天文学联合会（International Astronomical Union, IAU）明确新的标准历元为2000年1月1.5日TT，记为J2000.0。因此本文以J2000.0为标准年。

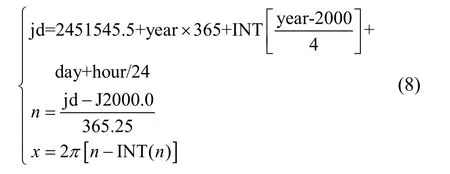
式中：jd为儒略日，year为计算的年份，day为一年中的积日，hour为一天中的小时数，n为将时间变量转换为弧度x计算公式的中间变量，INT为取整标准函数。其中n-INT(n)，限定了0≤x≤2π的取值范围。采用儒略历元计算时间参数，不仅包涵了奇偶年的时间变化，而且将离散的日期变为连续数字，便于计算，达到以年为周期的时间数据标准化的目的。

以太阳赤纬角为例，据文献[17]中所述，太阳赤纬公式可写成如式（9）所示：

式中： an为经验常数，n= 1, 2, …, 9。

最小二乘法的数学原理为：给定一组数据（xi,yii= 1, 2, …,n），设其经验方程为F(x)，方程中含有一些待定系数an。将xi代入方程F(x)并求其与yi的误差的平方和，即：

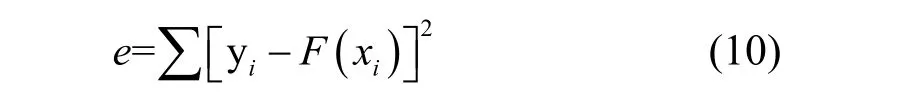
通过求e的极小值得到最优的an为经验常数。为得到更准确的拟合公式，与前人取特殊时间点参数的方法不同，本文取年历中全年数据作为最小二乘法拟合数据源，赤纬角拟合结果如式（11）所示：

3.2 计算结果分析

与柯伯方程相比，数值模拟法与理论展开式法在优化日间太阳方位变化的同时均充分考虑了年际间的地球轨迹变化。在世界气象组织（World Meteorological Organization, WMO）的《气象仪器和方法观测指南》推荐 Michalsky提出的基于理论展开式的简化计算方法，该方法计算误差小于0.01°[18]。将新拟合公式得出的结果与 Michalsky法计算结果进行对比，结果如图6所示。改进后拟合公式的太阳赤纬角计算误差不仅小于传统拟合公式的计算结果，而且与计算复杂的理论展开式法的计算误差相差无几，绝对误差值小于0.01°。图7为三种方程复合辐射计算的相对误差对比图。如图所示，高精度的太阳方位算法极大地减小了辐射计算的误差，较之柯伯方程的计算误差提升一个数量级，使得由于太阳方位计算误差对最终辐射计算结果造成的相对误差均小于0.2%。

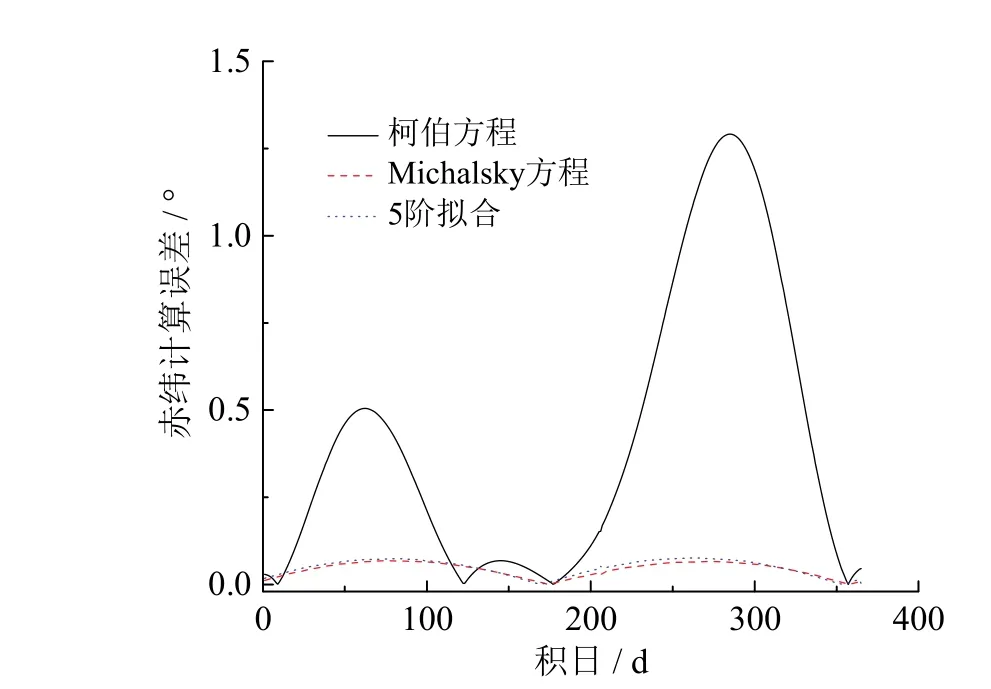
图6 太阳赤纬的绝对误差对比图Fig. 6 Absolute declination of the solar declination

图7 复合辐射计算的年日均辐射相对误差对比图Fig. 7 Calculated annual average radiation relative error by composite radiation

4 结 论

本文以辐射计算中必须使用的大气层外水平面辐射的计算为研究基础，对比分析了太阳方位参数（赤纬、日地距离）等计算误差程度对辐射计算结果造成的影响。结果显示，柯伯方程赤纬最大计算误差1.29°，对日均辐射计算结果造成的最大计算误差高达3%。日地距离计算误差（即偏心修正系数）对辐射计算结果的影响较小，对日均辐射计算结果造成的最大计算误差小于0.3%。一方面，两因素共同作用下年日均辐射量计算误差在1%左右。尽管1%的年日均辐射计算误差对工程领域应用的影响并不明显，但是太阳方位算法对辐射计算结果造成的不良影响完全可通过高精度的太阳方位算法降低甚至消除。另一方面，由于太阳方位参数的计算误差会带来日出和日落之间时间点计算差异，从而产生符号相异的极大误差，对之后的辐射数值计算带来巨大的误差。

针对以上两方面问题，引入儒略日作为时间变量和采用大数据量最小二乘法拟合得到一种改进的数值模拟法，将计算结果与 Michalsky法以及柯伯方程计算结果进行对比。结果表明，本文方法保持计算简单的原则同时其计算精度与计算复杂的Michalsky法相差无几。高精度的太阳方位算法不仅能够降低日出和日落之间过渡点的辐射计算误差，而且对日均辐射量计算结果造成的误差影响均小于0.2%。