求解Toeplitz线性系统的迭代方法

邵新慧, 张振铎

(东北大学 理学院, 辽宁 沈阳 110819)

现代很多领域在实际发展中,矩阵计算和方程组求解已经成为不能回避的核心重要问题.往往在特定的学科和环境下,特殊矩阵的分析和计算突显出重要的地位.本文讨论的Toeplitz矩阵在数字信号处理,流体力学中就有极其广泛的应用,因此寻找Toeplitz矩阵线性方程组的快速算法就显得尤为重要[1-2].较早的求解方法,主要将精力放在直接方法上,且成果显著,复杂度为O(n3),Toeplitz矩阵由2n-1个元素决定,所以研究者希望得到更低复杂度的算法[3].后来,迭代法成为研究重点,有研究者试图通过分裂Toeplitz矩阵从而迭代求解线性方程组[4-8].这一思路较早的应用是Bai提出的HSS方法[9].很多学者也在文献[9]基础上又给出了一些改进方法[10-12].后来,Micheal.K.G针对Toeplitz矩阵的特殊结构,提出了CSCS方法[13],即将Toeplitz矩阵分裂成一个循环和一个反循环矩阵,再进行双步迭代求解.而后,在2013年,N.Akhondi和F.Toutounian提出了加速CSCS方法,即ACSCS[14],它是在CSCS方法上,将单一参数形式改进成为了双参数的形式,在理论和实验结果上,都取得了较好的结果.最新相关Toeplitz系统求解的研究进展,在一些文献中提到[15].

本文在Micheal.K.G给出的CSCS方法基础上,提出了新的算法,称其为改进复参数CSCS方法,并将计算范围推广至复数域并引入两个不同的复参数进行分裂计算,并给出了新方法的理论分析证明.数值算例的结果表明新方法优于之前的算法.

1 CSCS算法及其改进算法

对于给定的Toeplitz矩阵的n×n阶方程组Ax=b.其中

是Toeplitz矩阵.Toeplitz矩阵A具有循环和反循环分裂A=C+S,其中:

这里C是循环矩阵,S是反循环矩阵.由此,提出了一种基于循环/反循环分裂迭代的非Hermitian Toeplitz系统的迭代Toeplitz求解法(CSCS迭代)如下:

CSCS迭代方法:给定初始假定x(0),对于k=0,1,2,…直到{x(k)}收敛,计算:

这里α是正常数.

理论证明,若C和S都是正定的矩阵,CSCS方法将收敛到唯一解.

基于Michael K.Ng的CSCS方法,在2012年,N.Akhondi和F.Toutounian提出了加速循环与反循环分裂法,即ACSCS方法.此方法中将CSCS方法中的单参数迭代形式,改为了双参数的迭代形式:

ACSCS方法具体如下.

给定初始假定x(0),对于k=0,1,2,…直到{x(k)}收敛,计算:

其中α为给定的非负常数,β为正常数.

理论分析表明,如果有效矩阵A是Hermitian正定的,且β在适当的区域被限制,对于任何给定非负α的线性系统,ACSCS迭代可以收敛到的唯一解.ACSCS迭代的收敛因子的上限取决于α,β以及循环矩阵C的谱和反循环矩阵S.理论上,ACSCS的收敛速度是O(nlongn).在实际的数值实验中,ACSCS方法的效率优于CSCS方法.

与之前不同的是,对Toeplitz矩阵A进行循环和反循环分解时,为了保障矩阵C和S的正定性,对A的分裂形式进行了调整.在这里C和S的推广形式如下:

其中0<β<1.

矩阵A可以做下面形式的分解:

(3)

其中,α=θ1+η1i,β=θ2+η2i,(θ1>0,θ2>0,η1≥0,η2≥0),矩阵C和S满足式(1)和式(2).

迭代格式如下:给定初始假定x(0),对于k=0,1,2,…直到{x(k)}收敛,计算:

其中:I是n阶单位阵;α,β和矩阵C,S均在式(3)中说明.

引理1[9]令A∈Cn×n,A=Mi-Ni(i=1,2)是矩阵A的双步分裂,x(0)∈Rn是给定的初始向量,如果{x(k)}是一个双步迭代序列,且满足

那么

定理1 令矩阵A∈Cn×n是一个Toeplitz矩阵,C和S分别为循环矩阵和饭循环矩阵,满足A=C+S,α=θ1+η1i,β=θ2+η2i,(θ1>0,η1≥0,θ2>0,η2≥0).如果C和S是正定的,那么改进CSCS方法的参数符合下面的限制

则有ρ(M(α,β))<1.此时对于给定的初始向量x(0)∈Rn,迭代序列{x(k)}都收敛于方程的精确解.

证明 由式(4),代入迭代阵,有下式

则,迭代矩阵的谱有下上限

其中

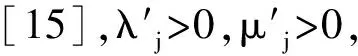
可以保证ρ(M(α,β))<σ(α,β)<1,即新算法收敛.

2 数值算例

以下例子均是针对(3-1)形式的Toeplitz方程组,其中的系数和常数矩阵均是计算机随机生成,迭代终止准则均为

首先给出一个小例子简单展示出改进复参数CSCS方法在计算复数域Toeplitz时的效率.

例1 对于5阶Toeplitz矩阵方程组

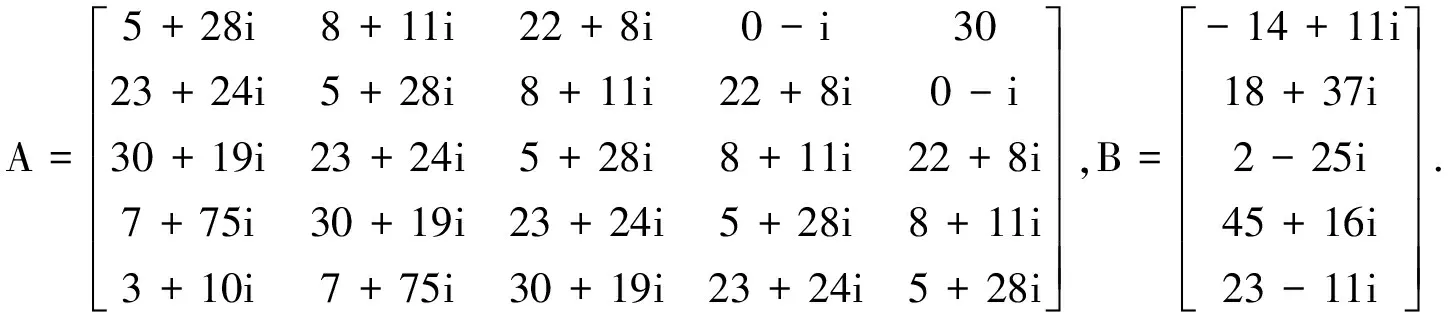
在这里先考虑是传统的CSCS方法.当两个参数相同,取不同值时的计算迭代情况.

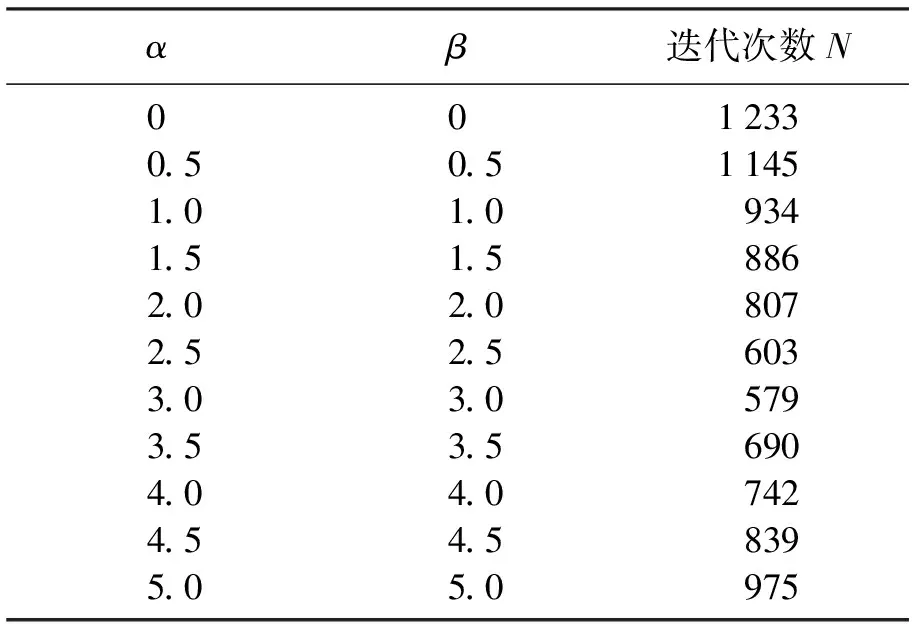
表1 传统CSCS方法1Table 1 Traditional CSCS method 1

可见,当参数达到3左右时达到了最佳的计算效果,579步左右.下面将展示改进复参数CSCS方法的计算结果,其中参数的实部选取的并不是传统CSCS最佳的参数3,而是选择的2,最后将看到再适当选择复数部时,最佳效果将优于传统CSCS选取最佳参数时的结果.

比较当α=β=2+0.1i时和α=2+0.17i,β=2+0.1i时, 可以清楚的看到改进算法的效果, 即双参数较之单参数的效率提高, 并且在后者情况, 计算步数在实部不变的情况下达到了最小值.

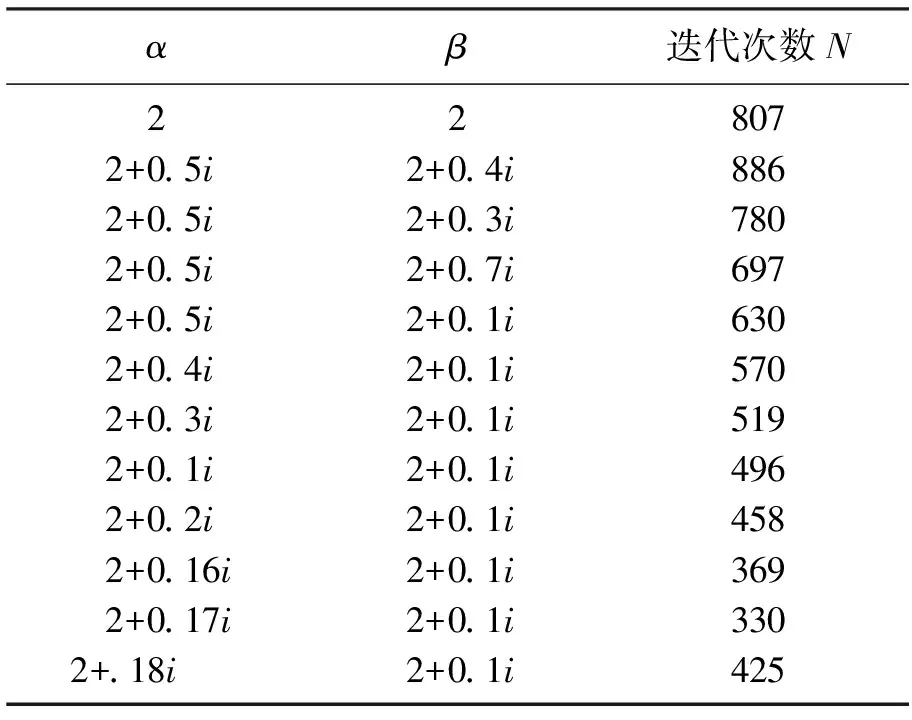
表2 改进复参数CSCS方法1Table 2 Improved complex parameters CSCS method 1

可见,即使实部选取不是传统CSCS方法最优的参数,改进CSCS方法也可以得到优于传统CSCS的结果,最优达到了330步,较之前有579步有很大提高.

同时,也可以看到在实部不变的情况下,随着虚部的调整,迭代步数明显的变少,这说明引入复参数确实增加了计算效率.

例2 对于7阶Toeplitz矩阵方程组

事实上,适当选取参数的实部可以大大提高计算效率.在本例中将说明这一点.下面是不同参数选择时的迭代情况.

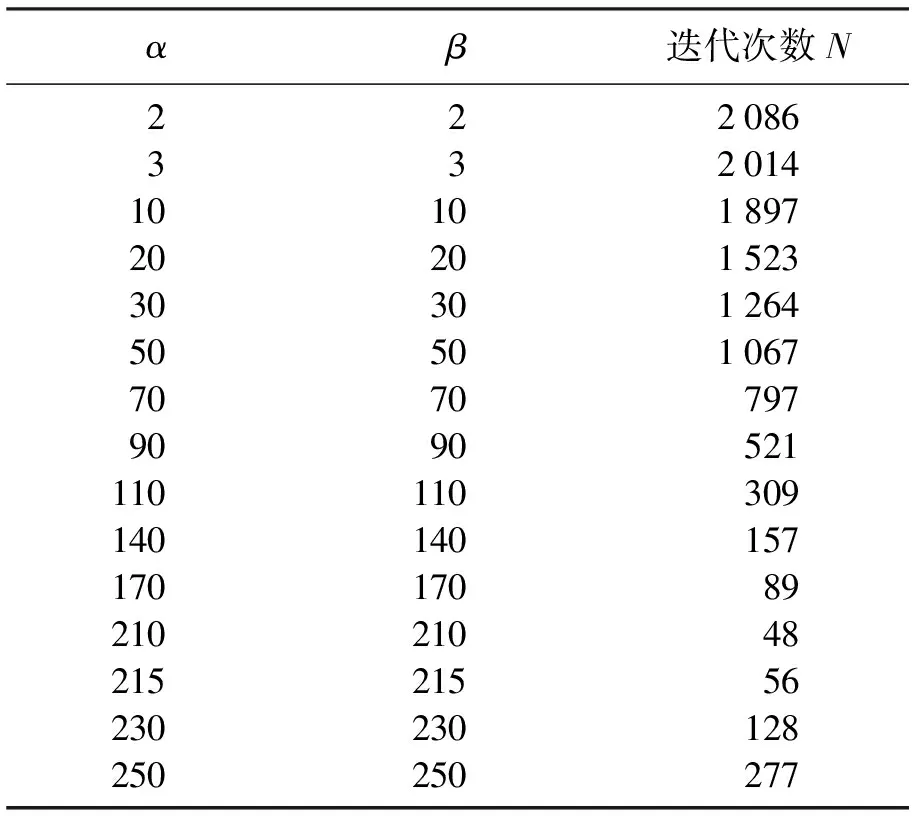
表3 传统CSCS方法2Table 3 Traditional CSCS method 2

可见,当参数选取210时,计算效率达到了最佳,细致的参数选择对计算影响很大.下面将展示改进复参数CSCS方法,

这里的参数实数部分将选择传统CSCS方法的最优参数210.

表4 改进复参数CSCS方法2Table 4 Improved complex parameters CSCS method 2

首先可以明显的看出实数部选择对计算效率的影响,事实上,通过调试,当两个参数取210是传统CSCS方法能达到最快时的取值,由于此讨论不是本文重点,在此做出说明即可.

当实部取最优参数时,通过调整虚数部分依然可以有效提高计算效率.改进的复参数CSCS方法较之前的方法从48步提高到了38步,效率提高了20%.

以上例子说明,在求解复数域Toeplitz系统时,改进CSCS方法是确实有效且快速的.

4 总结与展望

回顾了CSCS算法的同时提出了改进的算法,新算法能够适应更广泛种类的矩阵,而不是同传统的CSCS算法一样只用于实矩阵,这样的方法有广泛的实用性.由于参数可以调节,而不是原有的一个参数的类型,这提高了算法的效率,且具有较好的稳定性.

综上所述,改进后的CSCS算法有着比传统CSCS算法更好的计算效果,并且改进后的算法克服了复数域矩阵计算这一问题,更加合理,应用范围更广.