决策树模型在Ⅱ型糖尿病诊断中的应用

关红钧, 马尔丽

(1. 沈阳大学 师范学院, 辽宁 沈阳 110044;2. 沈阳师范大学 数学与系统科学学院, 辽宁 沈阳 110034)

Ⅱ型糖尿病是非传染性代谢性疾病,九成以上病人在35～40岁之间发病,糖尿病的特点是遗传易感性,在一些环境条件下可以触发其发病.随着互联网的迅猛发展和人们生活方式的改变以及人口老龄化,Ⅱ型糖尿病的发病率逐年提高,特别是发展中国家增加速度更快,且具有流行势态.在全球范围内,糖尿病是继心血管病和肿瘤之后,对人们健康和生命造成危害的重大非传染性疾病.因此,预防Ⅱ型糖尿病的发生发展,控制糖尿病患病人数具有重要意义.到目前为止,国内外有一些文献研究疾病建模问题[1-6],决策树建模方法备受关注[7-8].本文利用数据挖掘C4.5和CART算法构建简单的决策树模型,建立Ⅱ型糖尿病诊断模型,以此挖掘糖尿病的患病因素,为糖尿病的预防和临床诊断工作提供理论依据.

1 Ⅱ型糖尿病诊断模型建模方法

1.1 研究对象

本文数据资料来源于河北省秦皇岛市某医院糖尿病患者病例.数据包括:性别、年龄、烟龄、身高、体重、收缩压、舒张压、甘油三酯、总胆固醇、低密度脂蛋白、糖尿病家族史、高血压家族史、心脑血管病史、冠心病史、空腹血糖、家族史、既往史和高血压史.

1.2 建模方法

Quinlan开发的C4.5算法是机器学习算法中的一种代表决策树算法,是升级版的ID3算法.分类决策树算法是在大量的样本集合中进行训练,要求每个拆分点仅有两个支系构成,从而能够避免属性选择的不平等问题.C4.5算法拥有着ID3算法的优点,并对ID3 算法进行了改进:使用信息增益率来选择属性,解决ID3算法中用信息增益来选择属性时偏向样本数目多的属性的缺点;在构成树的过程中进行剪枝,并非在建成之后剪枝,快速地完成对其连续属性的离散化处理和对样本内部缺失数据的处理.

CART决策树算法是在1984年由Breiman提出的.如果当前目标变量是分类变量时,则是分类树;如果目标变量是定量变量时,则为回归树.它以迭代的方式,从树根开始反复建立二叉树[2].考虑一个具有两类因变量的两个特征变量的数据.CART算法是每次选择一个特征变量将区域分成为两个半平面,经过持续不断地划分之后,特征区间被分成了矩形区域.CART决策树使用基尼指数来划分属性.

决策树模型的CART算法由JMP实现,C4.5由R3.4.2实现.

2 Ⅱ型糖尿病诊断模型的建立

2.1 决策树模型

通过无放回抽样方法,在这组样本中抽取1/4构成497例测试样本, 抽取3/4构成1425例训练样本.分别用两种算法建立模型,模型共有17个变量:Sex、Age、BMI、SBP、DBP、TG、CHOL、LDL、GLU、FMH、PH、SL、HH、CHDH、CCDH和FHH.决策树的根节点样本总数为1425,即训练样本总体.决策树挖掘深度为4,最后进入C4.5模型的是3个变量:GLU、FMH和CCDH,叶节点个数为2,进入CART模型的变量有8个:GLU、FMH、CCDH、FH、SL、SEX、DBP和Age.

(1) C4.5决策树模型

C4.5模型如图1所示:C4.5决策树的左支表示糖尿病患者,其余表示非糖尿病患者.如果GLU(空腹血糖)指标<6.1,则可以诊断为没有患该病;如果GLU>6.1,并且FMH=false(无糖尿病家族史),即可诊断为没有患病;如果有糖尿病家族史,需要观测CCDH(心脑血管家族史),如果CCDH=FALSE(没有心脑血管家族史),则没有患病;否则即为患病.

(2) CART模型

图1 C4.5决策树模型
Fig.1 Decision tree model of C4.5

CART模型如图2所示:C4.5决策树的左支表示糖尿病患者,其余表示非糖尿病患者.如果GLU(空腹血糖)指标<6.09,则可以诊断为没有患该病;如果GLU>6.09,并且FMH=false(无糖尿病家族史),即可诊断为没有患病;如果有糖尿病家族史,需要观测CCDH(心脑血管家族史),如果CCDH=FALSE(没有心脑血管家族史),则没有患病;否则即为患病.如果PH(没有冠心病病史),则没有患病;否则即为患病.

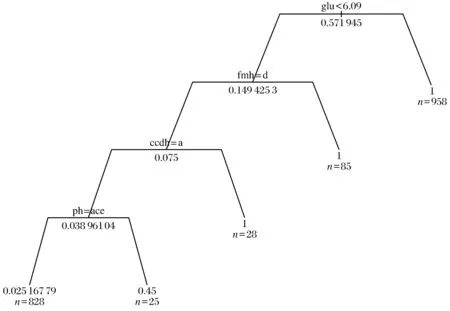
图2 C4.5决策树模型Fig.2 Decision tree model of C4.5

2.2 模型比较

(1) 方法比较

对糖尿病数据执行JMP决策树图,如表1所示,此时提示空腹血糖(GLU)变量应作为拆分树的首要节点.在对于D中元组分类中,需要期望信息如下式所示:

Info(D)又称为熵.

假定划分D中元组是按照属性A,且将D划分为v个不同的类也是按照属性A.划分后,为了使分类准确,下面的式子度量来完成需要的信息:

原来的信息需求就是仅基于类比例,新信息需求就是对A划分之后得到的值.用原来的信息需求与新需求之间的差来定义信息增益,即

Gain(A)=Info(D)-InfoA(D),

其中,G2是对数似然比统计量,它是对数熵的两倍,拆分节点是使信息增益最大,如图3所示.

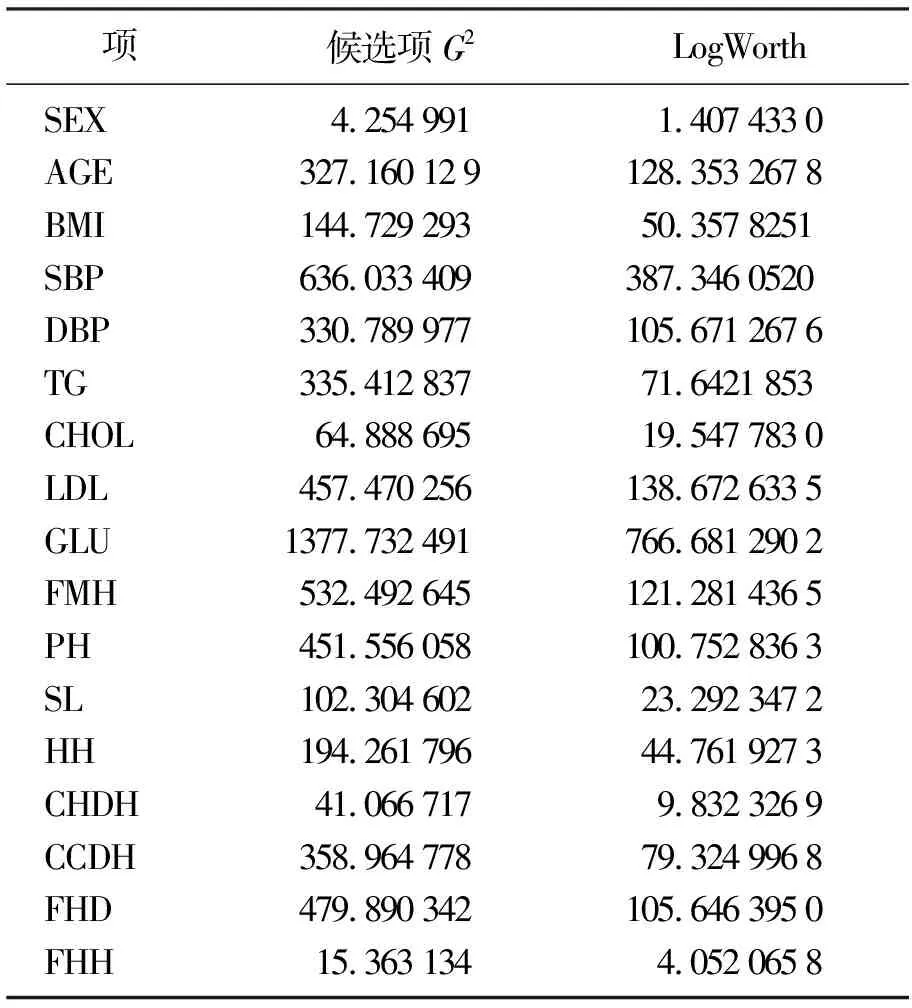
表1 候选项拆分的重要性结果Table 1 Results of importance of candidate item splitting

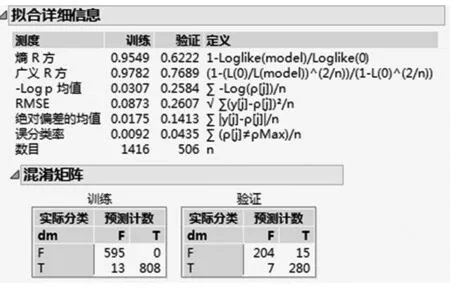
图3 拟合信息详情Fig.3 Fitting information details

图3中dm是指糖尿病,T表示患病,F表示没有患病.拟合详细信息中列出了基本的描述树效果的统计量,定义栏给出了相应统计量计算公式.含混矩阵下分别对训练样本和验证样本的预测效果和验证样本的预测情况作了统计,可以看出预测结果偏向于样本多的类别,这也是决策树设计中存在的问题.

(2) 结果比较

利用已建立的模型,预测测试样本中的诊断结果,进而对该模型进行评价.

预测结果显示,结果如表2所示:CART模型优于C4.5模型,但C4.5方法更为准确.

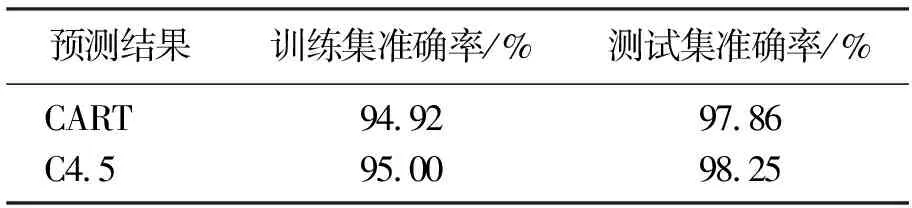
表2 CART算法和C4.5算法的预测结果Table 2 Predictions of CART and C4.5 algorithm

3 结 论

本文利用决策树算法建立了糖尿病模型,简单明了,解读性强,具有一定的临床参考价值.从模型中可以看出空腹血糖、糖尿病家族史、心脑血管既往病史等是Ⅱ型糖尿病发病的重要因素.此外,模型评价说明利用CART模型挖掘临床检验资料有一定价值,直观易理解.但由于数据和地域的影响,后续工作仍需要大量的数据和调查资料,合理建立模型,客观评价模型.