锂原子基态变分法的研究

□董良杰

(山西广播电视大学,山西 太原 030027)

在物理方面,多粒子体系经常会被我们遇到。类似于经典力学,很难解决多粒子体系相互作用的问题。事实上,它不能被严格解决,而只能近似求解。量子力学中,两种常用的近似方法是微扰法和变分法。本文将采用变分法对简单的多粒子体系(锂原子)的基态进行研究。

一、物理学中的变分法

(一)变分法的思想

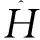
Ε0,Ε1,Ε2,…Εn…

(1)

这些本征值对应的本征函数是

Ψ0,Ψ1,Ψ2,…Ψn…

(2)

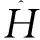
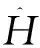
Ψn=ΕnΨn

(3)

假使Ψ为归一的任一波函数,将Ψ按Ψn展开,则有

Ψ=∑anΨn

(4)

在Ψ描绘的状态中,系统能量的期望值是

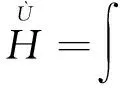
Ψ*ΗΨdτ

(5)

将(4)式代入(5)式中,则得

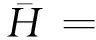
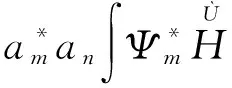
(6)

应用(3)式有

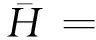
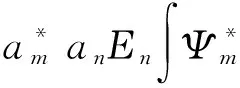
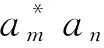
(7)

由于Ε0是基态能量,所以有Ε0<Εn(n=1,2,3,…),在上式中用Ε0代Εn,则

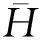
≥Ε0∑|an|2=Ε0

(8)

最后一步用了Ψ的归一化条件:∑|an|2=1

(7)和(8)式给出:

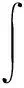
(9)

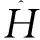
在上述讨论中,假定Ψ是归一化的,如果Ψ不归一化,那么(5)式应写为

(10)

(9)式则应写为

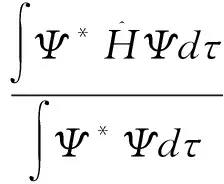
(11)

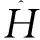
(二)变分法计算基态能量和波函数的步骤

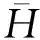
(12)

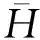
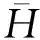
(三)变分法的价值

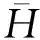
二、用变分法计算锂原子的基态能量及波函数

锂原子是有两个电子处于1s态,一个价电子处于2s态的多电子体系。为此,锂原子的哈密顿量可写为:

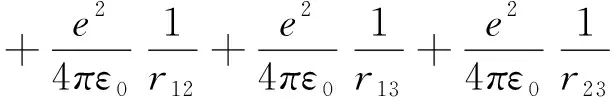
(13)

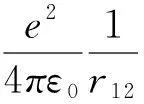
(一)选取合适的尝试波函数

将(13)式进行重组,则此式可写成:

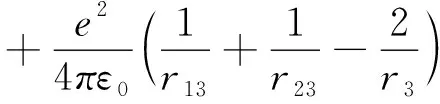
(14)

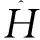
因为锂原子的1s电子几乎不受2s电子的屏蔽,所以锂原子的1s态下的波函数选择Li+的两个1s电子波函数u(r)代表。所以,锂原子1s态下的尝试波函数为[5]:

(15)

此外,锂原子的两个1s电子对2s电子有一定的屏蔽,2s电子受到的有效电荷相当于类氢原子,故而,采用类氢原子的基态波函数作为2s态下的尝试波函数[3]:

(16)

式中λ=1+σ,(σ≥0)σ刻画屏蔽效应的大小。若σ=0,则λ=1,表示无屏蔽。且2s电子遵循薛定谔方程:

υ(r3)=

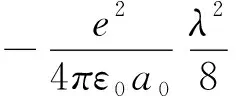
(17)

当忽略电子波函数的交换对称性时,锂原子的尝试波函数可写为

ψ=u(r1)u(r2)υ(r3)

(18)

(二)变分法计算基态能量和波函数

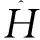
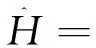
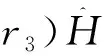
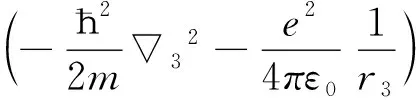
u2(r1)u2(r2)υ2(r3)dτ1dτ2dτ3

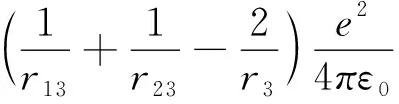
u2(r1)u2(r2)υ2(r3)dτ1dτ2dτ3

(19)

υ2(r3)dτ3

(20)

由于J项中r13和r23较难处理,可近似将r13、r23看作r3和r3,则

u2(r1)u2(r2)υ2(r3)

u2(r1)u2(r2)υ2(r3)=0

(21)

可得:

(22)

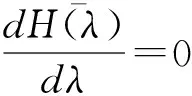
λ=1

(23)

所以

.936(eV)

(24)

然后我们将λ代入试探波函数,得到锂原子的基态波函数为:

ψ=u(r1)u(r2)υ(r3)

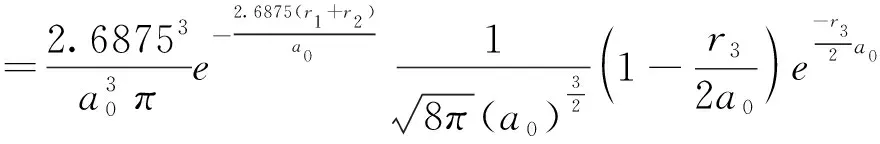
(25)

三、结论

我们知道,在实验中测得的锂原子基态能量为-203.345eV,而在此次论文中算出的数值与实验值的误差为1.68%。造成如此大的误差原因主要是:忽略了电子的交换对称性;同时,在计算J项时,我们近似处理了1s的两个电子与2s上的电子间的相互距离。例如,将第1个和第3个电子的间距看作是将第1个电子放在核上,由此第1个和第3个电子的间距就变成了核与第3个电子的间距,即r13=r3。同理,r23=r3。因此,锂原子基态能量的计算值具有比理论值有较大的误差。