货车车轮与重载固定辙叉弹塑性接触分析
2018-11-07刘晓东封全保
刘晓东,张 军,马 贺,封全保
(1.北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室,北京 100044;2.清华大学天津高端装备研究院,天津 300300)
辙叉是铁路轨道实现列车转线运行的主要结构。由于固定型辙叉具有维修工作量小、造价低、易安装等优点,在我国时速低于160 km的既有线路和重载线路上得到了广泛的应用[1-2]。由于其复杂的轮轨关系,导致道岔区钢轨磨耗严重,主要表现为翼轨磨耗异常、心轨出现剥离掉块等(如图1所示),直接影响辙叉的打磨周期和使用寿命,并给列车行车安全带来一定的隐患[3]。随着重载铁路运量的不断增加与速度的不断提高,辙叉损伤表现得更为突出,因此对轮叉接触进行深入分析已成为重要课题[4]。

图1 辙叉区伤损
针对上述问题,专家学者不仅从道岔刚度[5-6]、辙叉内部应力状态等方面研究提出延长辙叉使用寿命的措施与方法,并且通过有限元法对固定辙叉进行了大量分析与研究。文献[7]通过分析辙叉内部应力状态提出了延长辙叉使用寿命的建议;文献[8]通过有限元程序对不同辙叉进行对比分析,总结出高锰钢固定型辙叉结构破坏的主要原因与改进措施;文献[9]通过建立有限元模型,对75 kg/m钢轨12#固定辙叉的薄弱部位进行强度验算并提出改进措施;文献[10]通过分析动态模型得出心轨受损的主要因素是接触压力;文献[11]通过建立模型,分析了道岔结构不平顺性对轮叉接触的影响。现有大量研究均基于标准型面进行分析,但在列车实际运行中,标准型面存在时间相对较短,因此研究磨耗后轮叉型面的接触分析尤为重要。
本文针对大秦重载铁路75 kg/m钢轨12#固定型辙叉磨耗严重问题,应用轮轨型面测量仪对服役的货车车轮和固定辙叉进行型面测量,得到磨耗后车轮型面与固定辙叉关键型面数据,建立弹塑性接触有限元模型,分析车轮与辙叉接触时的接触斑形状与面积、接触轨迹以及等效应力的变化规律,总结车轮对辙叉翼轨、心轨的磨耗影响。
1 计算理论
车轮在心轨与翼轨之间过渡时,由于复杂的轮轨关系,相互作用剧烈,导致接触区域存在较大的接触应力,使得部分材料发生塑性变形。考虑轮叉接触的局部塑性变形,采用双线性随动强化弹塑性材料模型作为轮轨弹塑性计算的本构关系,服从Von Mises屈服准则与随动强化准则。
Von Mises屈服准则遵循畸变能密度理论,该理论认为引起材料屈服的主要因素是畸变能密度,即无论什么应力状态,只要畸变能密度达到与材料性质有关的某一极限值(屈服极限)时,材料发生屈服,进入塑性变形阶段。该屈服准则可用下式描述。
(1)
式中:σe为等效应力;σ1,σ2,σ3为某点的3个主应力;σs为材料屈服强度。
根据弹塑性理论,双线性强化塑性材料的应力σ与应变ε的关系为
(2)
式中:Ee为弹性模量;EP为应变强化模量;εs为屈服点总应变。
辙叉材质为高锰钢,其材料参数为:Ee=205 GPa,Ep=20.5 GPa,σs=689.6 MPa。假设车轮与辙叉材料相同,用2条斜直线简化材料的应力-应变关系,如图2所示,其中2条直线的斜率分别为材料的弹性模量与强化模量。
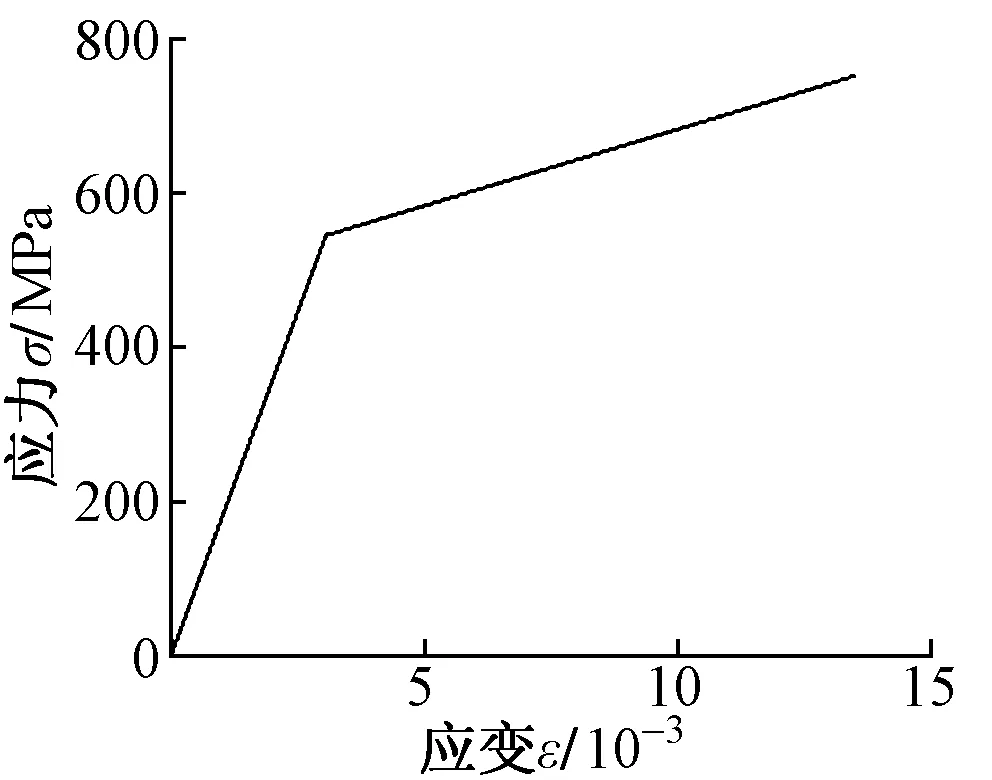
图2 材料应力-应变曲线
2 有限元模型的建立
对重载铁路道岔伤损现状进行调研后发现,固定型辙叉的伤损范围主要集中在心轨理论尖端至心轨轨顶宽40 mm范围内。利用轮轨型面测量仪测得大秦重载铁路固定型辙叉关键截面与车轮型面数据,辙叉区关键截面以理论尖端为基准,向心轨加宽的方向选取5个型面,其关键截面如图3所示。
图3 辙叉关键截面位置分布(单位:mm)
将测量的车轮与辙叉型面数据处理后选出具有代表性的型面进行模型的建立与分析[12-13],选取的车轮与辙叉型面如图4和图5所示。与标准车轮相比较,磨耗后车轮踏面中部与踏面外侧均有所磨耗,但踏面中部磨耗较严重。图5中标准辙叉型面与磨耗后辙叉型面比较可发现,磨耗后辙叉的翼轨与心轨均磨耗,其中翼轨的磨耗主要集中在内侧,心轨的磨耗主要集中在轨顶处。
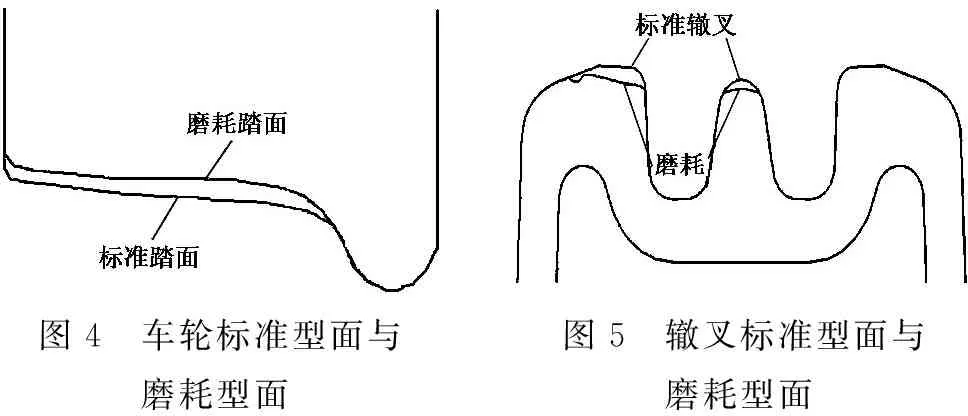
图4 车轮标准型面与磨耗型面图5 辙叉标准型面与磨耗型面
由于轮叉接触区面积远远小于接触表面的曲率半径,可知接触区存在明显的应力集中,因此将轮叉接触区域网格细化,尺寸为1 mm单元,轮叉接触有限元模型如图6所示。

图6 轮叉接触有限元模型
模型计算参数如下:轨距为 1 435 mm,轮缘内侧距为 1 353 mm,车辆车轮直径为840 mm,施加轴重为25 t。辙叉底部施加固定约束,以限制其3个方向的位移与转动;约束车轮在水平面内的平动与绕各个轴的转动。轮叉间摩擦类型选用罚函数模型,摩擦系数为0.4,泊松比为0.3。
3 计算结果分析
固定型辙叉由翼轨和心轨组成,列车与辙叉的不同位置接触时,不同的车轮对辙叉的影响存在一定的差异。本文建立标准车轮与标准辙叉、标准车轮与磨耗辙叉、磨耗车轮与标准辙叉和磨耗车轮与磨耗辙叉4种匹配形式的接触模型,分析其接触斑形状与面积、接触轨迹以及等效应力的变化规律。
3.1 接触斑形状分析

图7 翼轨与心轨上接触斑形状
车轮与辙叉接触时在不同的匹配形式下其接触斑形状的变化规律基本一致,但车轮在辙叉的翼轨和心轨上时接触斑形状存在一定的差异。图7为标准车轮与标准辙叉匹配时距离理论尖端240 mm和480 mm处接触斑形状,在距离理论尖端240 mm处车轮与辙叉的翼轨接触,其接触斑形状相对细长;在距离理论尖端480 mm处车轮与辙叉的心轨接触,其接触斑形状接近椭圆形状。
图8为不同匹配方式时各关键位置的接触斑的分布情况。就接触斑形状而言,车轮与辙叉接触时接触斑形状均呈细长条状,长轴沿着纵向,短轴沿着横向。但不同匹配方式时接触斑形状存在一定的差异。标准车轮与标准辙叉匹配时,接触斑形状为细长条,长短轴之比较大;标准车轮与磨耗辙叉匹配和磨耗车轮与标准辙叉匹配时,在距离理论尖端240 mm位置处均出现极其细长的接触斑,如图8(b)与图8(c)所示,极其细长的接触斑将导致轮叉接触应力集中,根据磨耗磨损的一般规律,此匹配方式在距离理论尖端240 mm 附近区域辙叉磨耗较为严重。计算结果与现场观察基本一致。

图8 不同匹配方式时接触斑分布
3.2 接触斑面积分析
不同轮叉匹配形式在距离理论尖端不同位置处接触斑面积见表1。对比分析可得,标准车轮与磨耗辙叉和磨耗车轮与标准辙叉匹配时,在距离理论尖端240 mm位置处接触斑面积分别为24.45,45.51 mm2,接触斑面积在此位置出现骤降,为过渡区域内最小接触面积,结合图8(b)与图8(c)中该位置极其细长条状的接触斑形状分析,推断此2种匹配方式将对辙叉翼轨造成较严重的磨耗磨损现象。
表1不同轮叉匹配方式下不同位置接触斑面积
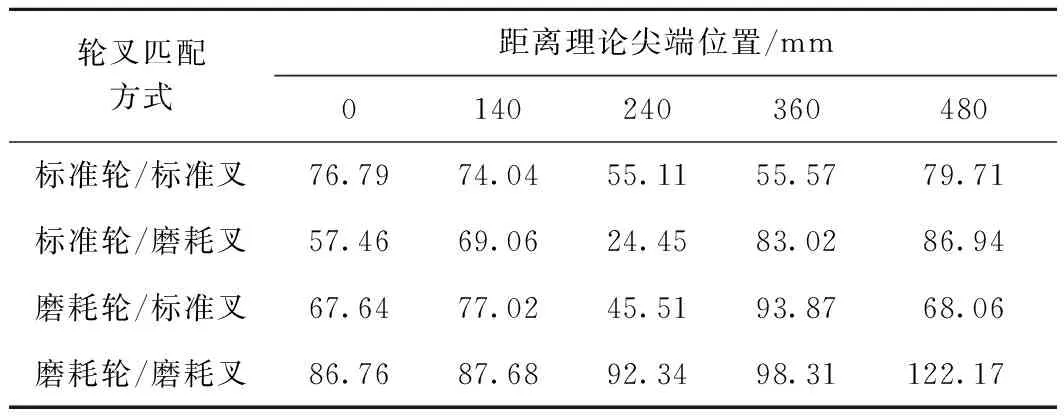
mm2
标准车轮与标准辙叉和磨耗车轮与磨耗辙叉匹配时,关键位置截面处的接触斑面积变化趋势较平缓,没有出现面积突变的现象。磨耗车轮与磨耗辙叉匹配时接触斑面积均大于标准车轮与标准辙叉匹配时,且接触斑形状更近似椭圆形。结合接触斑形状分析,磨耗车轮与磨耗辙叉匹配效果更佳,为较理想的轮叉型面匹配方式。
3.3 接触轨迹分析
辙叉上接触斑的分布可以直观地反映轮叉接触时的接触轨迹。分析图8可知,车轮由翼轨向心轨过渡时,接触轨迹的变化趋势基本一致。在列车通过辙叉时,接触斑位置逐渐向翼轨的内侧移动,最终实现向心轨的过渡。不同的匹配方式下接触斑的大小与形状存在一定的差异,标准车轮与标准辙叉和标准车轮与磨耗辙叉2种方式匹配时,由翼轨向心轨的过渡位置在距离理论尖端240~360 mm区域内,如图8(a)与图8(b) 所示;而磨耗车轮与标准辙叉和磨耗车轮与磨耗辙叉2种方式匹配时,其过渡位置在距离理论尖端360~480 mm区域内,与标准车轮相比较有延后的趋势,如图8(c)与图8(d)所示。
由于列车在实现由翼轨向心轨过渡时,车轮与辙叉的接触位置由踏面的远离轮缘侧变为踏面中部,而磨耗后车轮踏面中部的磨耗导致在向心轨过渡时接触位置延后。标准车轮通过辙叉时其过渡位置为距离理论尖端240~360 mm区域内,由于线路上标准轮叉型面存在时间相对短暂,绝大部分均为磨耗车轮与磨耗辙叉,可推断车轮通过辙叉时过渡位置为距离理论尖端360~480 mm区域内。
图8(d)为磨耗车轮与磨耗辙叉匹配时接触斑的分布情况,接触斑形状在短轴方向有所增加,使长短轴之比减小,形状更接近椭圆形,此种匹配方式将分散轮叉接触应力,降低对辙叉的磨耗。
3.4 等效应力分析
图9为距离理论尖端不同位置处不同匹配方式下轮叉间最大等效应力对比。可知车轮通过辙叉时,最大等效应力均超过了材料的屈服极限,进入塑性变形阶段。

图9 最大等效应力对比
不同匹配方式下轮叉间最大等效应力分布存在一定的差异,标准车轮通过标准辙叉时最大等效应力在 1 062~2 118 MPa,标准车轮通过磨耗辙叉时最大等效应力在970.7~1 490 MPa,且2种匹配方式下的等效应力最大值均出现在距离理论尖端240 mm 位置处,分别为 2 118,1 490 MPa。过大的应力集中将加剧材料的塑性流动,造成辙叉的异常磨耗,分析表明标准车轮通过辙叉时在距离理论尖端240 mm 附近辙叉翼轨磨耗严重,磨损异常,与实际情况相符。
磨耗车轮通过磨耗辙叉时最大等效应力在841.1~1 066 MPa,变化幅度为26.7%,与其他匹配方式相比,最大等效应力均较小,未出现过大的应力集中现象。图10为该匹配方式下距离理论尖端360 mm位置处等效应力分布云图,可知最大等效应力分布在距离接触表面以下2 mm范围内,接触斑形状近似椭圆,接触斑面积较大,有利于分散轮叉之间的应力,延缓辙叉的磨耗。
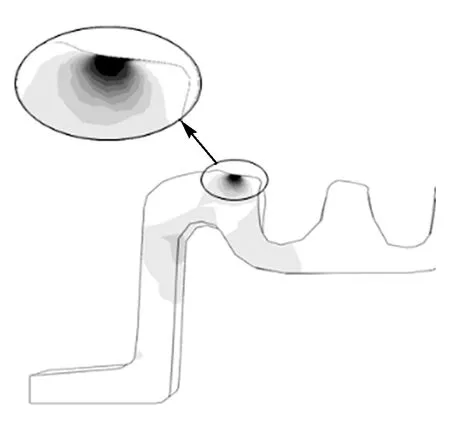
图10 距离理论尖端360 mm处等效应力分布云图
4 结论
本文通过有限元法,建立不同轮叉型面匹配的有限元模型,求解轮叉间弹塑性接触问题,通过大量计算得出车轮与辙叉接触时的接触斑形状与面积、接触轨迹以及等效应力的变化规律,结论如下:
1)微小的塑性变形可使材料硬化,延缓辙叉的磨耗,但是车轮通过辙叉时,轮叉间等效应力均超过材料的屈服极限,进入塑性变形阶段,过大的应力集中将加剧材料的塑性流动,导致磨耗严重,磨损异常,辙叉的使用寿命得不到保证。
2)通过分析接触斑的形状与面积以及等效应力可知,在距离理论尖端240 mm位置处和车轮通过辙叉时翼轨与心轨过渡区域均为辙叉区的薄弱环节,应力集中易导致辙叉出现剥离掉块现象,存在一定的安全隐患。
3)与其他匹配形式相比较,磨耗后车轮与磨耗后辙叉匹配时,接触斑形状的长短轴之比较小,更接近椭圆形,接触斑面积较大,最大等效应力较小,所以,这种匹配方式为较理想的匹配方式,可以延缓辙叉的磨耗。
