特殊桥梁结构无缝线路附加纵向力计算方法

丁静波，刘亚航，乔神路

(中铁工程设计咨询集团有限公司 轨道院，北京 100055)

在温度荷载和列车荷载作用下，桥梁和轨道的结构设计应考虑梁体与无缝线路相互作用而产生的附加纵向力，包括伸缩力(T1)、挠曲力(T2)、断轨力(T3)、制动力(T4)。计算无缝线路附加纵向力时，应首先确定设计参数，建立无缝线路计算模型，然后输入温度荷载、列车荷载，计算附加纵向力和位移。其中无缝线路模型是计算的关键之一[1]，可采用大型有限元软件建立三维空间耦合的实体模型[2]，目前大部分为简易模型。

无缝线路简易模型是将轨道、桥梁及墩台简化为梁、板单元，但实际桥梁结构非常复杂，难以精确模拟[3]。以铁路总公司通用参考图中(60+100+60)m标准混凝土连续梁为例，其中支点处梁高为7.2 m，连续梁中间10 m直线段及边跨15.75 m直线段梁高为4.6 m，梁底下缘按二次抛物线变化[4]，这种非线性变化截面难以准确模拟。城市轨道交通常用的U形梁属于开口薄壁结构，在荷载作用下，轨道变形复杂，按常规模型也难以准确模拟。特别是铁路用钢桁梁结构，与一般混凝土桥梁不同，其弹性模量、截面惯性矩等参数无法简单提取。类似还有斜拉桥、拱桥等。因此该模型通常与实际桥梁结构差异较大，影响桥上无缝线路附加纵向力的计算准确性。

针对上述问题，本文通过理论分析，基于有限元刚度法(位移法)，建立无缝线路附加纵向力简易模型，直接加载位移，利用梁、轨位移与纵向阻力间关系，计算无缝线路各种附加纵向力。

1 特殊桥梁结构无缝线路计算方法

1.1 梁、轨相互作用原理

任取梁体和钢轨组合的一个微段dx为自由体，分析梁、轨相互作用和位移平衡条件。桥梁跨度为L，梁体刚度为E1J(其中E1为梁体的弹性模量，J为梁体的截面惯性距)。在列车活载q作用下，梁体和钢轨发生挠曲变形，梁体各截面的位移Δx实际上是梁体平移和旋转的组合。其中上翼缘的位移在固定支座端最大，下翼缘的位移受固定支座的约束，在固定支座端最小或为0。梁的中性轴至上、下翼缘的距离为h1，h2，则梁上翼缘距梁端距离为lx处的位移[5]为

(1)

梁体的位移Δx和钢轨位移y与线路纵向阻力p(z)有关。

与此类似，在温度荷载作用下，任意梁截面伸缩位移Δxt为

Δxt=αΔTL

(2)

式中：α为梁的线膨胀系数；ΔT为环境温度的变化量。

根据钢轨的拉伸和压缩变形平衡条件Σωi/EF=0(其中Σωi为钢轨拉伸和压缩力面积之和，E为钢轨弹性模量，F为钢轨截面积)，以及梁、轨间位移相等条件，即y-Δx=0，求解钢轨位移、相对位移及附加纵向力。

通过以上分析可见，上翼缘的挠曲位移Δx、梁体的伸缩位移Δxt是产生附加纵向力的必要条件，且通过线路纵向阻力p(z)与钢轨附加纵向力发生关系。

1.2 特殊桥跨结构无缝线路设计方法

有限元刚度法(位移法)的基础方程为总体节点力T和总体节点位移d通过总体刚度矩阵K相互关联，其形式为T=Kd。其中K矩阵的单元刚度系数Kij需要根据模型确定，Kij代表在j自由度产生单位位移dj时在i自由度所需要的力Ti。合理确定位移函数，利用钢轨的拉伸和压缩变形平衡条件和梁、轨间位移相等条件，以及节点力与节点位移方程，最终求解单元力[6]。

基于上述思路，针对特殊复杂的桥梁结构，直接将纵向水平位移Δx，Δxt加载至简化的无缝线路模型中，利用线路纵向阻力使钢轨附加纵向力与桥梁位移产生关系，并根据钢轨拉伸和压缩平衡方程，及梁、轨间位移相等条件，求解钢轨附加力。图1为无缝线路附加纵向力计算模型，采用梁单元模拟钢轨，采用非线性弹簧单元K1，K2模拟线路纵向阻力，采用空间板单元模拟桥梁截面，并采用弹簧或杆单元K3模拟桥梁的水平线刚度[7]。将不同的纵向水平位移输出数据施加于梁体进行分析计算，可弥补原轨道模型的不足，计算更符合实际，更加精准，适用于特殊复杂桥梁结构，例如U形梁、钢桁架梁等。

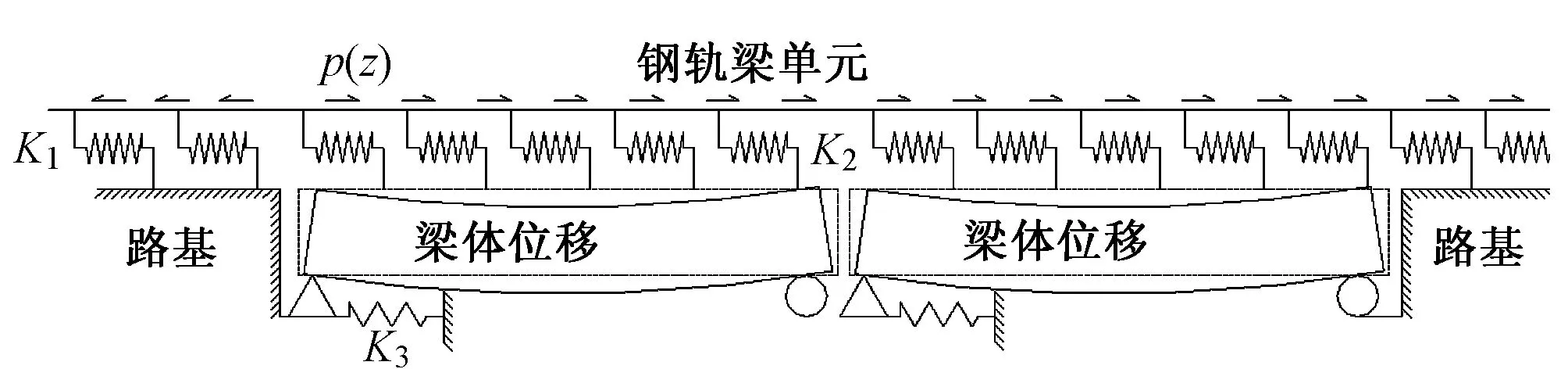
图1 无缝线路附加纵向力计算模型

2 应用实例

2.1 城市轨道交通U形梁

U形梁是目前城市轨道交通普遍采用的结构形式之一，具有建筑高度低、断面空间利用率高、降噪效果好、行车安全、外形美观等优点[8]。它属于下承式开口薄壁结构，梁体由底板、两侧的腹板和顶部上翼缘连成U字形横截面，轨道结构通过预埋钢筋与U形梁联接成一个整体，如图2所示。U形梁内外散热快，与环境温度相等，避免了箱梁的内外温差现象，有利于无缝线路铺设。但U形梁的轨道结构不是位于常规的上翼缘位置，其变形与梁体刚度E1J、梁高h1等参数的关系与常规梁体差异较大。本文采用位移法计算无缝线路附加纵向力。

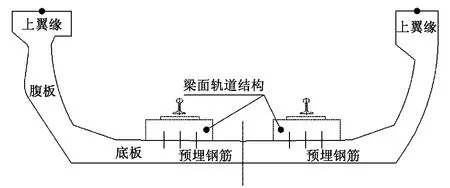
图2 城市轨道交通U形梁结构示意

以30 m简支U形梁为例，在均布荷载q=31 kN/m作用下，求解出U形梁底板中间节点的纵向位移，如表1所示。

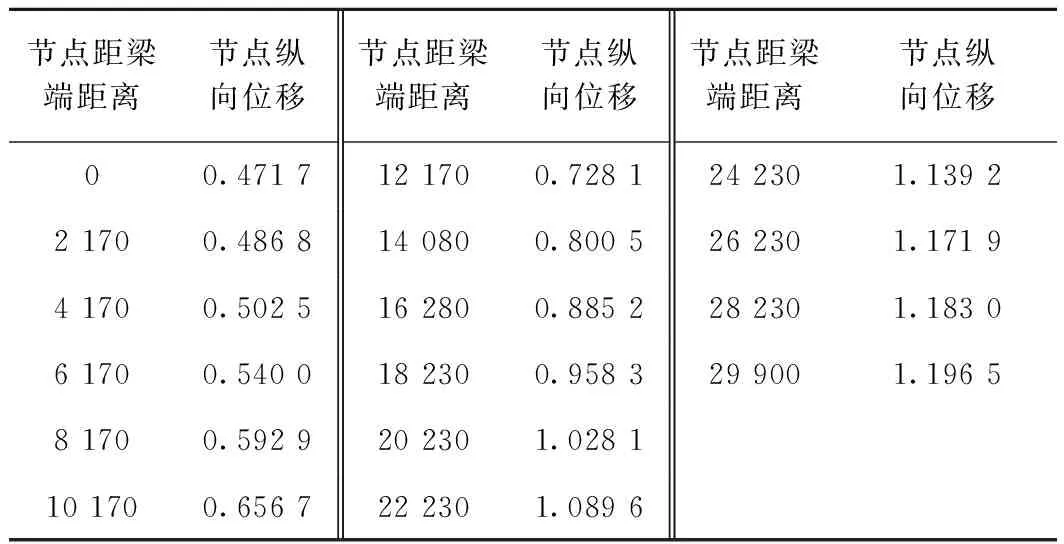
表1 U形梁底板中间节点纵向位移 mm

根据表1数据，采用式(1)进行数据拟合，结果如图3所示。其吻合度与多项式的幂次方数有直接关系，幂次方越高越精确。

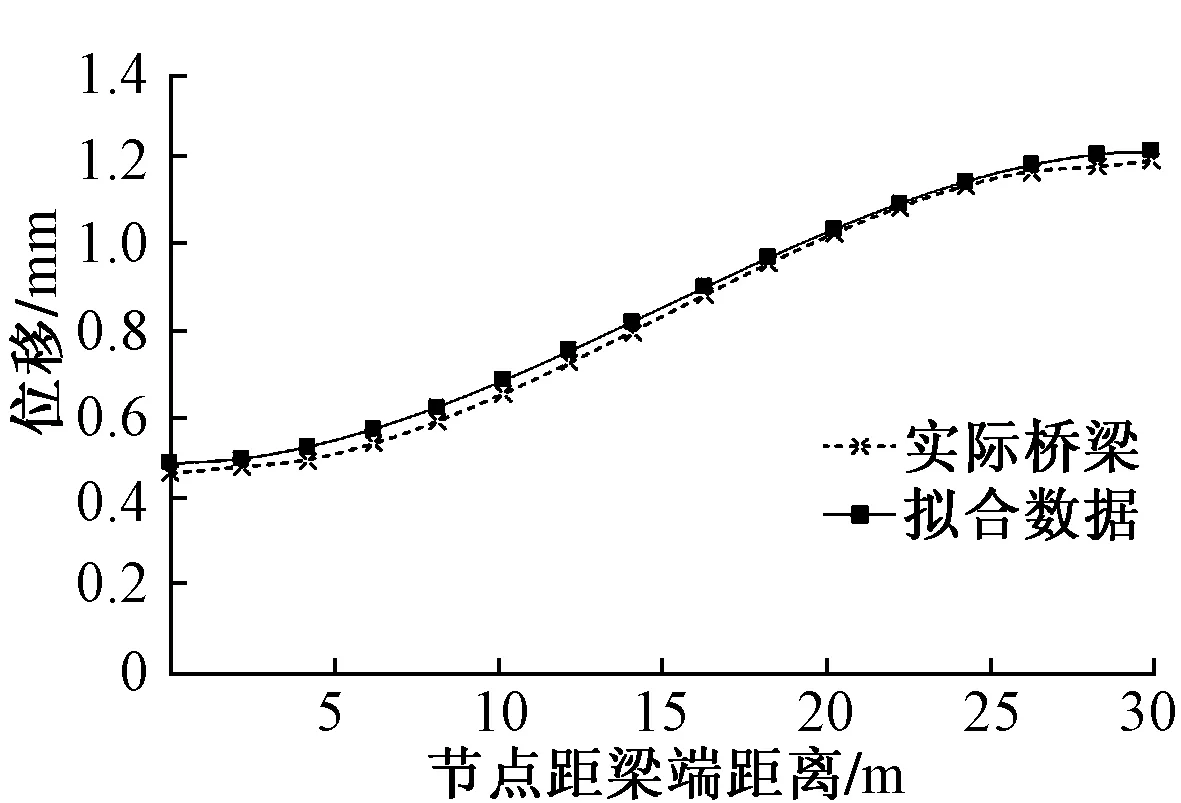
图3 U形梁位移拟合数据

然后通过有限元程序将位移直接加载在梁单元上，计算无缝线路附加纵向力。求得钢轨最大拉力为73.774 kN，最大压力为46.614 kN，则30 m简支U形梁附加纵向力为：车下挠曲力T2=68.20 kN/轨，车前挠曲力T2=53.03 kN/轨，见图4。

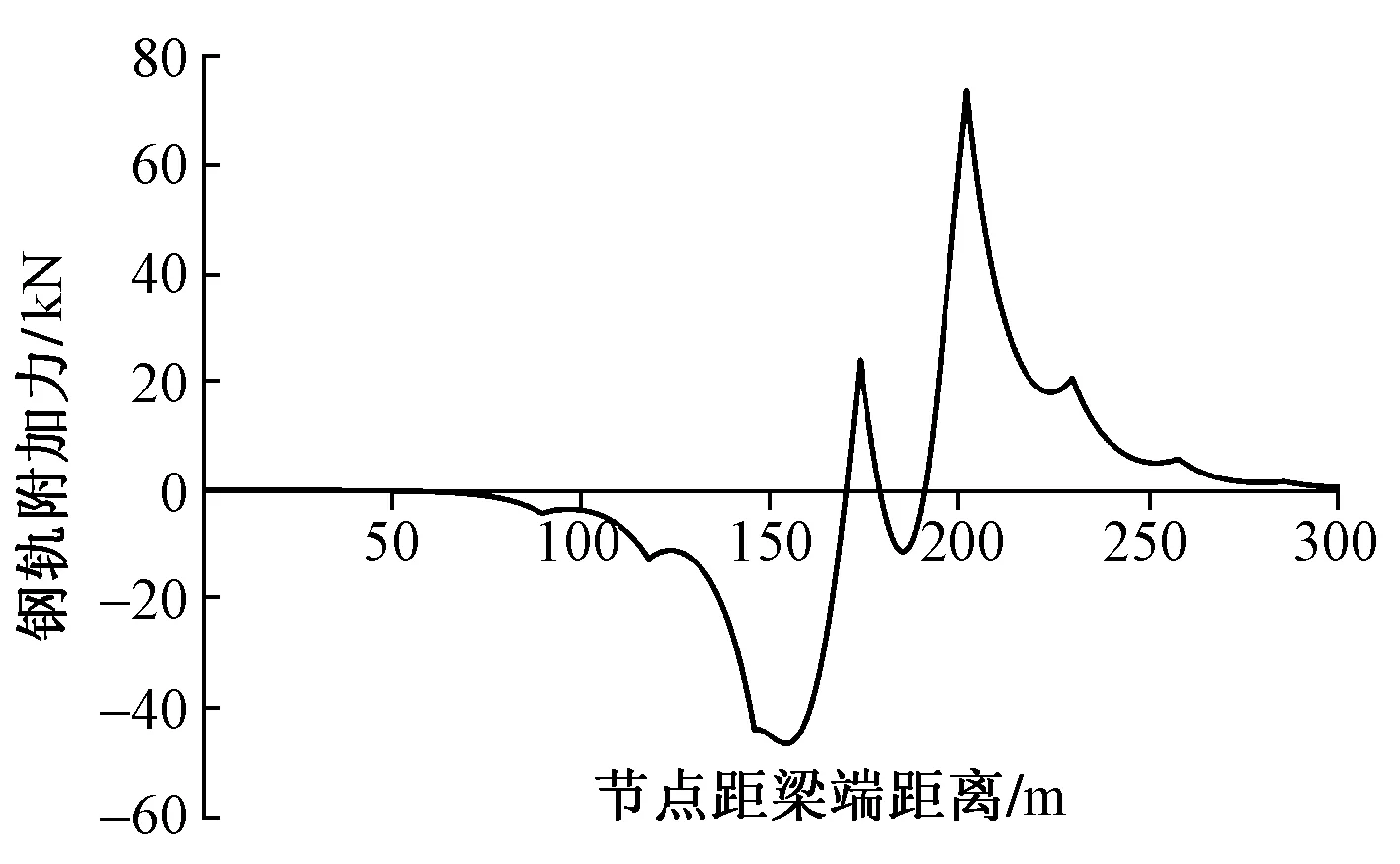
图4 30 m简支U形梁轨道附加纵向力T2

2.2 高速铁路钢桁梁

钢桁梁适用于高速铁路、普速铁路、重载铁路及城市轨道交通等，由边桁、主桁、联结系及桥面组成，结构复杂[9]。以某高速铁路公铁两用双层120 m简支钢桁梁为例建立有限元模型，上层为快速公路，下层为高速铁路，桁梁采用华伦式桁架，边桁桁高15 m，中桁桁高15.24 m，节间长12.06 m，主桁采用三片桁，桁宽为2×13.4 m。

桥上铺设CRTSⅠ型双块式无砟轨道结构，按TBJ 24—89《铁路结合梁设计规定》相关要求，应考虑活载、温度变化所产生的内力。120 m简支钢桁梁中桁节点在整体升温30 ℃、顶板降温10 ℃以及最大活载作用下最大纵向位移及铁路、公路制动力下顺桥向位移结果见表2。

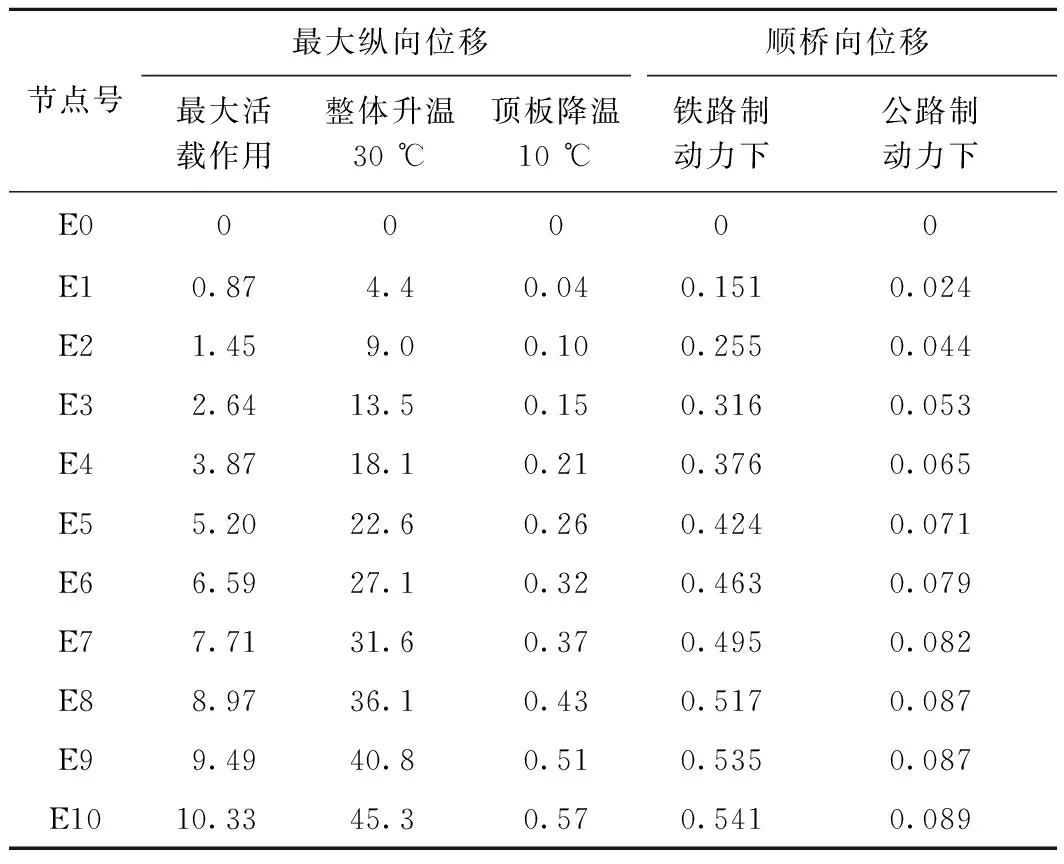
表2 120 m简支钢桁梁中桁节点位移 mm

无缝线路常规计算模型仅能考虑整体升温条件，很难考虑结构整体变形差异。例如针对上述公铁两用双层钢桁梁，分析顶板降温收缩对下部承轨面变形的影响，常规模型虽然与实际桥梁模型的位移变化趋势基本一致，但数值略低于实际桥梁模型，差异见图5。

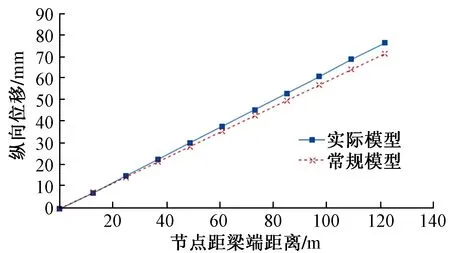
图5 常规模型和实际模型的位移差异

参考国内外相关资料[10-13]，考虑极端铺设条件对无砟轨道的影响。上述公铁两用双层120 m简支钢桁梁在整体升温50 ℃、顶板降温20 ℃工况下[12]，采用位移法计算得到钢轨最大拉力为415.331 kN，最大压力为416.374 kN，对桥墩最大伸缩力T1=484.441 kN/轨，见图6；在活载位移下，钢轨最大拉力为67.256 kN，最大压力为55.377 kN，车下挠曲力T2=38.61 kN/轨，车前挠曲力T2=90.289 kN/轨，见图7；在铁路和公路制动力下，钢轨最大拉力为112.325 kN，最大压力为113.238 kN，见图8。另采用BCWR软件，直接在桥梁施加温度荷载，计算得到钢轨最大拉力为432.534 kN，最大压力为439.831 kN，伸缩力T1=552.365 kN/轨；仅在桥梁施加UIC活载制动，计算得到钢轨最大拉力为131.741 kN，最大压力为123.616 kN，由于桥梁实际模型下制动位移小，BCWR软件计算得到的制动力大于位移法模型制动力；但BCWR软件无法计算钢桁梁结构挠曲力。通过输出实际桥梁位移的方法，简化无缝线路计算模型及参数，计算结果与实际更加吻合。

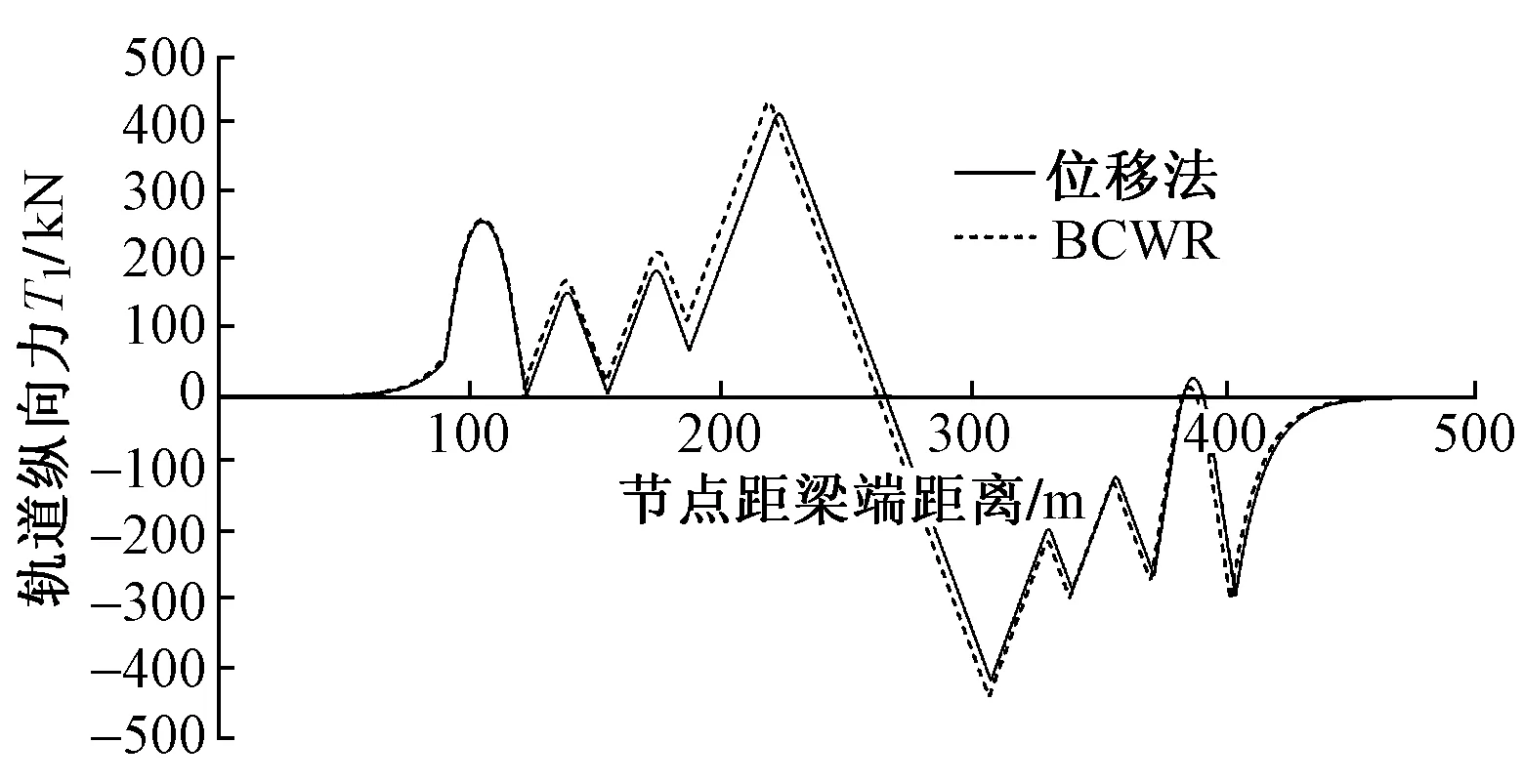
图6 高速铁路用120 m钢桁梁温度附加纵向力T1

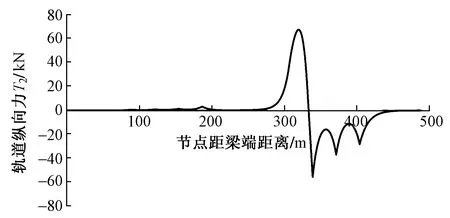
图7 高速铁路用120 m钢桁梁挠曲附加纵向力T2

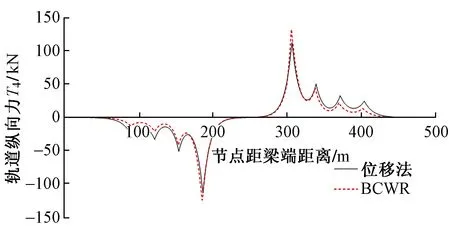
图8 高速铁路用120 m钢桁梁制动附加纵向力T4

3 结论及建议

1)上述模拟位移计算附加纵向力的方法可适用于温度、列车活载等不同工况下各种桥梁和轨道间无缝线路的附加纵向力，特别适用于U形梁、钢桁梁、拱桥、斜拉桥等复杂桥型，弥补了原轨道模型的不足。

2)由于实际桥梁在温度、列车活载等荷载作用下，存在不均匀性或离散性，特别是桥墩水平线刚度对纵向水平位移存在影响，本文通过输出实际位移数据，分析轨道附加力及相对位移，与原轨道模型计算数据进行对比分析可知，其计算精度更高。

3)这种特殊桥梁结构无缝线路纵向力计算方法已应用于南京、上海等地的地铁U形梁结构，及山西中南部铁路[13]、包神线铁路黄河特大桥等钢桁梁桥[14]，以及南广西江桥(41.2+486.0+49.1)m中承式钢箱提篮拱桥等特殊桥梁结构[15]。

4)一般桥梁模型很少考虑制动工况，制动力对桥梁结构的影响较小，建议结合具体工程实际，合理选择无缝线路计算模型。