基坑开挖引起的邻近地铁隧道纵向变形计算方法

2018-11-07徐闻达

铁道建筑 2018年9期

徐闻达，蒋军

(浙江大学防灾工程研究所，浙江杭州 310058)

随着城市轨道交通和城市建设的高速发展，越来越多的基坑工程邻近既有的运营地铁隧道。这些邻近开挖会对既有地铁隧道产生不利影响，尤其对于软土地区的盾构隧道，可能引发隧道渗水漏泥，甚至严重影响隧道结构的稳定及运营安全。

近年来，基坑开挖对邻近隧道的影响受到了国内外诸多学者的关注。刘国彬等[1-2]根据开挖引起的残余应力场分析了隧道处土体的回弹，但该方法没有考虑隧道刚度的影响。张治国等[3]采用Mindlin解计算了开挖卸荷引起的隧道结构附加应力，然后基于Winkler地基模型推导出下卧隧道隆起的计算公式；张治国等[4]考虑坑底和坑壁同时卸荷的影响，提出了基坑开挖引起邻近地铁隧道纵向变形的两阶段分析法；周泽林等[5]考虑土体流变特性，采用Pasternak双参数地基模型得到隧道上抬变形的时域解；黄栩等[6]采用Kerr模型分析了土体卸荷所引起的隧道响应。然而，上述研究都忽略了隧道上覆土层对隧道结构的影响。SHI等[7-9]采用数值模拟方法，针对基坑开挖引起的邻近隧道的变形规律、受力特征、加固和保护措施等进行了多方面的研究。但这些分析多针对某个具体工程，未能对这类问题提出简便而实用的计算方法。

鉴于已有研究存在的不足以及数值建模复杂、计算耗时的缺点，本文在前人研究的基础上，提出基坑开挖引起的邻近隧道纵向变形的简化计算公式，通过算例验证其合理性。

1 基坑开挖引起的隧道纵向附加应力

1.1 建立力学计算模型

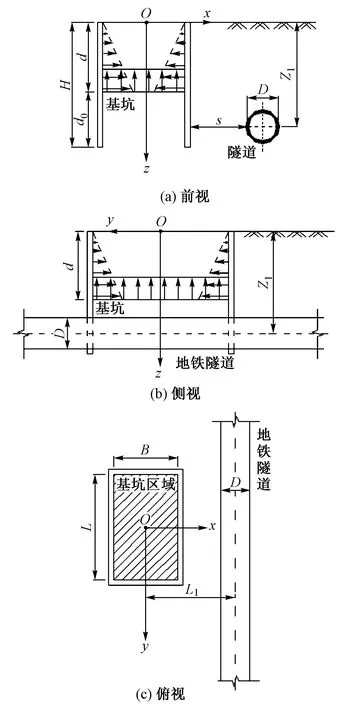
图1 基坑开挖对地铁隧道影响的计算模型

如图1所示，地铁隧道附近有一基坑，基坑底部高于隧道顶部，以基坑中心对应的地表点O为原点建立直角坐标系。基坑的开挖深度为d，长度为L，宽度为B，基坑开挖面到基坑围护结构底面的距离为d0，围护结构深度为H。地铁隧道横截面的宽度为D，地铁隧道中心线与基坑中心线距离为L1，隧道中心埋深为Z1，基坑侧壁与隧道的最小净距为s。

计算过程中假定：①土体为弹性半空间内的均质土体；②隧道纵轴线方向平行于基坑侧壁，隧道结构视为无限长均质弹性体，其截面保持不变；③不考虑基坑开挖的时间和空间因素，不考虑降水；④不考虑隧道存在对土体附加应力的影响。

1.2 计算公式推导

1)基坑侧壁卸荷分析

基坑开挖到坑底，坑壁四周应力释放，相当于在邻近坑壁施加指向坑内的三角形分布荷载，在基坑底面位置大小为K0γd。但基坑围护结构对侧向应力释放具有明显影响，即从静止土压力状态到主动土压力状态，比较两者的差值，引入应力折减系数β(按文献[10]建议取值)，则等效荷载变为βK0γd。由Mindlin解，在坑壁三角形分布荷载中一点(η，τ)的应力作用引起的隧道结构轴线上任意一点(L1,y1,z0)的水平附加应力σx为

(1)

式中：γ为土体重度；υ为泊松比；Ω是基坑侧壁的积分区域;K0为静止侧压力系数，可通过室内试验或原位静止侧压力试验测定，缺乏试验数据时可根据经验公式估算。砂性土的K0=1-sinφ，黏性土的K0=0.95-sinφ。

R1,R2为控制隧道与基坑侧壁中心相对位置的参数，分别为

2)坑底卸荷分析

由于不是弹性体，其变形包括弹性变形和塑性变形，因此开挖卸荷前后计算的应力不会完全相等，土中会留有残余应力[2]。残余应力系数α的计算公式为

(4)

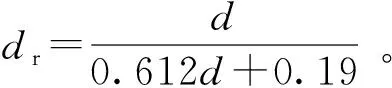
基坑开挖完成后坑底的土体应力释放，可将应力等效为向上的矩形均布荷载，大小为γd。由于基坑底面以下存在围护结构，坑底的等效荷载无法直接作用到邻近隧道上，因此需考虑围护结构的遮拦效应[11]。由于基坑围护结构的保护作用，坑底释放的应力会受到围护结构侧摩阻力qs的影响，计算公式为

(5)

式中：c为土的黏聚力;φ为土的内摩擦角。

因此，围护结构底面水平面上土体受到的等效荷载σ为

(6)

由Mindlin解可知，在围护结构底面水平面上某点(ξ,η)上力σdξdη作用下，引起的隧道结构轴线上一点(L1,y1,z0)竖向应力可用积分计算。隧道结构竖向附加应力σz可写为

(7)

式中:Γ为围护结构底面对应的积分区域。

T1,T2为控制隧道与基坑底面中心相对位置的参数，分别为

(8)

(9)

2 隧道纵向变形理论

城市地铁隧道一般建于深层土体中，直接应用Winkler弹性地基梁理论分析时，不能考虑上覆及周围土体对盾构隧道结构的约束作用[12]，为考虑这种影响，故采用双面弹性地基梁模型分析隧道的纵向变形。

建立如图2所示的直角坐标系，将隧道结构简化为一双面弹性地基梁，隧道上下部地基均视为土弹簧，其余假定同Winkler弹性地基梁模型。在隧道结构任意位置y处取微元段dy进行受力分析，如图3所示。图中:M为微元体受到的弯矩;Q为微元体受到的剪力。设微元体在由基坑开挖引起的附加荷载q(y)作用下，产生位移w(y)。弹性梁受到的下部弹性地基的反力为p1，上部弹性地基对梁的作用力为p2。

图2 双面弹性地基梁模型

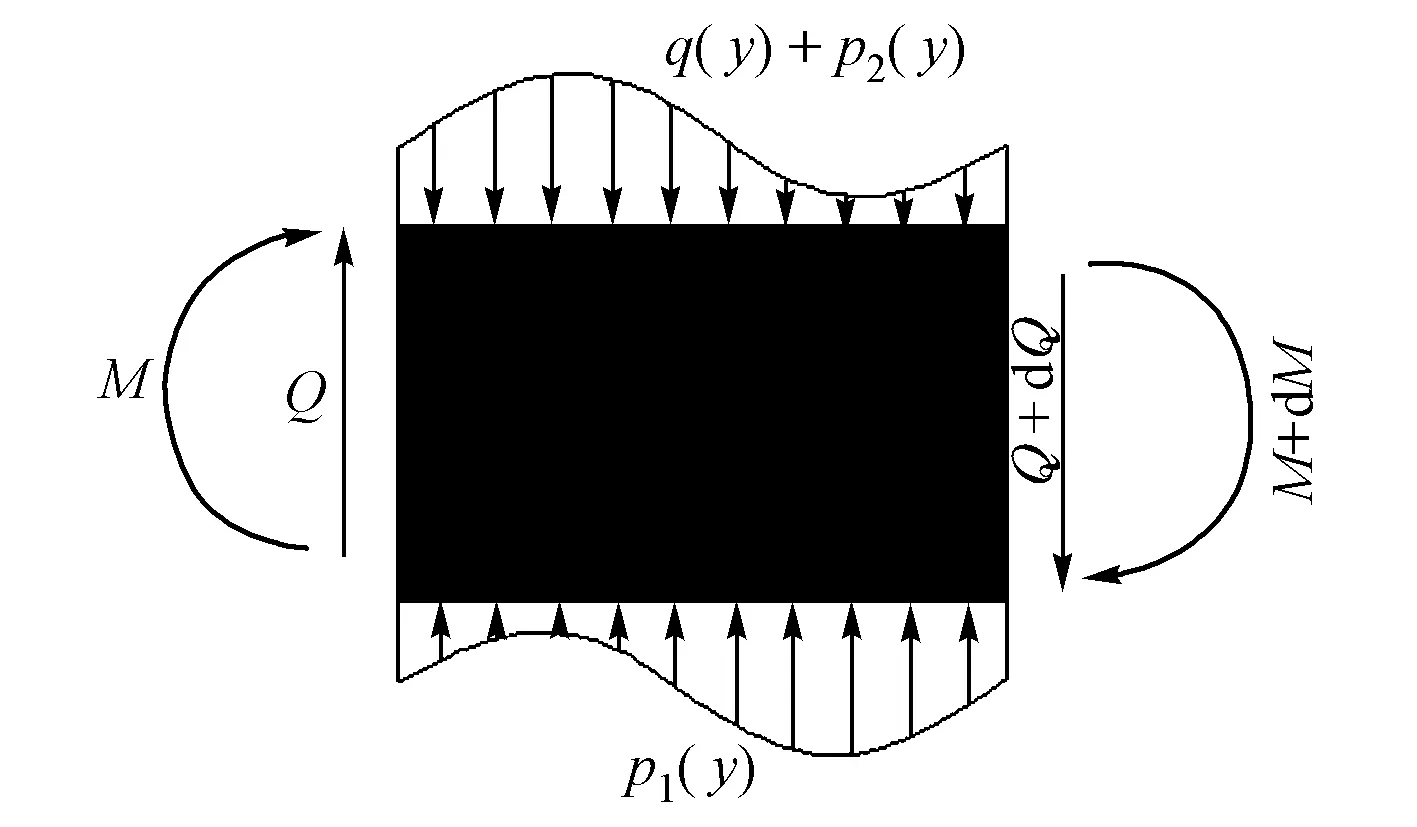
图3 微元体受力简图

根据平衡条件，得到隧道与土体相互作用的力学方程为

(10)

根据Winkler弹性地基梁理论，地基中该点所受到的应力只与该点的地基沉降sy成正比，因此

p1=k1sy

(11)

p2=-k2sy

(12)

式中：k1,k2分别为上、下部地基土体的基床系数。

本文假设地基为均质土体，上下部地基土体的基床系数相同，即k1=k2=k。由于变形连续协调，w(y)应与sy相等，从而得到梁的挠度微分方程

(13)

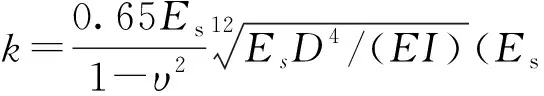
方程(13)是非齐次四阶常微分方程，采用有限差分法进行求解。从隧道取出微元段进行受力分析，如图4所示，分成n段，每段长度l，在两端补上虚节点，分别为-2,-1,n+1,n+2。

图4 有限差分网格

每分段的隧道位移分别为w0，w1，…，wn。第i分段的位移表达式为

(14)

根据差分原理，可将式(14)写成差分形式。

(15)

加上边界条件的4个方程，由此构成n+1个线性代数方程组，以此求得隧道各分段对应的位移wi，用矩阵的形式表示为

[A]{w}={q}

(16)

式中：[A]为隧道位移刚度矩阵;{w}为隧道位移列向量;{q}为附加荷载列向量。

3 算例验证

3.1 有限元算例

有一建设项目需要在既有地铁隧道附近进行基坑开挖，基坑平面尺寸为30 m × 18 m，开挖深度为 10 m。基坑围护结构采用地下连续墙，地下连续墙深度为18 m，厚度为0.8 m。其中基坑的短边与隧道平行，基坑开挖面与隧道最小净距为6 m，隧道外径为6 m，内径5.4 m，埋深12 m，隧道纵向等效抗弯刚度EI=7.8×107kN·m2。基坑场地为均质粉质黏土，土体重度γ=21 kN/m3，弹性模量E=12 MPa，黏聚力c=12 kPa，内摩擦角φ=20°，泊松比υ=0.35，基坑围护结构的应力折减系数β=25%。

隧道分段n=40，每段长度l=2 m，自编程序求得各分段水平与竖向位移，并借助有限元软件PLAXIS 3D进行验证。土体本构采用摩尔-库伦模型，隧道结构采用梁单元模拟，基坑及隧道周围加密网格，共生成 58 401 单元，86 993 节点，如图5所示。

图5 有限元网格

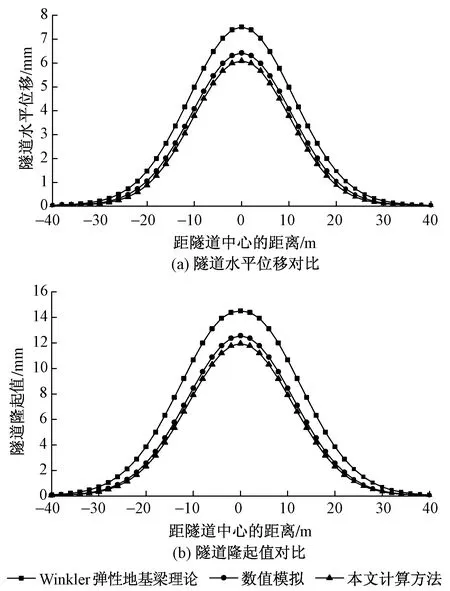
图6 3种不同计算方法结果对比

图6为采用本文方法与数值模拟、Winkler地基梁模型得到的计算结果对比。可以看出：3种计算方法得到的隧道纵向位移曲线分布规律基本相似，但数值存在一定差异，本文方法计算结果与数值模拟结果均明显小于Winkler弹性地基梁理论所得结果，本文方法所得结果更接近于数值模拟结果。因此，对于城市深埋地铁隧道，应用双面弹性地基梁理论进行变形分析比Winkler弹性地基梁理论更加精确，符合客观规律。

相比大型有限元软件，本文计算方法无需建模，计算速度快，采用本文方法可以初步评价基坑开挖对邻近地铁隧道的影响，从而采取相应措施。

3.2 工程实例

中国东部地区一建筑场地基坑，平面尺寸为30 m × 20 m，开挖深度为7 m。围护结构采用地下连续墙，在汉口路一侧，地下连续墙深15 m，厚0.8 m，内设一道水平支撑。地铁一号线区间隧道位于汉口路路面下，其中已建成的区间隧道下行线距基坑南侧地下连续墙仅4 m，与基坑宽度方向平行，隧道埋深10 m。隧道外径6 m，厚0.45 m，纵向等效抗弯刚度为7.21×107kN·m2，场地地质条件详见文献[10]。

文献 [10]将隧道结构视为弹性地基梁，提出基坑开挖对邻近隧道纵向位移的计算方法，并与工程实测数据进行了对比。图7为实测数据、文献[10]方法与本文计算方法所得结果对比。本文计算方法所得隧道最大隆起值为5.2 mm，略小于实测值5.7 mm；文献[10]方法所得最大隆起值为6.8 mm，与实测值偏差较大，误差约19.2%。究其原因，本文在文献[10]所提方法的基础上考虑了围护结构的遮拦效应以及上覆土层对隧道结构的影响，因此计算结果更加接近实测值，同时再次验证了所提方法的合理性。本文计算方法所得变形值与实测值略有偏差，这是由于本文计算方法没有考虑既有隧道对土体应力场的影响。此外，实际工程采用分段、分层的开挖方式，而本文计算方法中并未考虑基坑开挖的时空效应。