缺失数据场合下Frechet分布参数的逆矩估计
2018-11-07徐晓岭吴生荣
何 亮,徐晓岭,吴生荣
(1.上海对外经贸大学 统计与信息学院, 上海 201620; 2.宜兴出入境检验检疫局, 江苏 宜兴 214206)
在极值分布理论中,一般有三种类型的分布函数,即Gumbel分布、Frechet分布以及Weibull分布[1]。1927年Frechet[2]中推导出在初值非负的前提下最大极值分布的渐近分布表达式。1984年Mann[3]给出了Frechet分布与Gumbel分布之间的关系及其参数估计。Frechet分布在诸多领域有着广泛的应用,Longin[4]用Frechet分布拟合股市的极端价格变动走势,Harlow在文献[5]中说明Frechet分布经常被用在工程应用材料属性的统计模型中,Nadarajah[6]将Frechet分布用于社会学模型。Zaharim等[7]将对数正态分布以及Frechet分布用于风速数据的预测分析中。Mubarak[8]讨论了Frechet分布在逐步增加的定数截尾数据并包含随机移除场合下参数的最大似然估计以及区间估计。Abbas和汤银才[9]研究了在定数截尾数据场合下参数的最大似然估计以及最小二乘估计。Sindhu等[10]分别研究了定时截尾以及定数截尾数据场合下,Frechet分布形状参数已知情况下尺度参数的Bayes估计。曾林蕊等[11]给出了Frechet分布在定数截尾数据缺失场合下参数的近似极大似然估计。
本文首先研究了两参数Frechet分布的失效率函数与平均失效率函数,说明其图像均为“倒浴盆”曲线。给出了Frechet分布在缺失数据场合下两种逆矩估计,利用Monte-Carlo方法与文献[11]中的近似极大似然估计进行比较,说明了逆矩估计在样本量较小以及缺失数据较多情况下在均方误差意义上优于近似极大似然估计。
1 Frechet分布及参数的逆矩估计
1.1 Frechet分布的数学特征
设产品寿命T服从两参数Frechet分布,记为T~Fr(α,β),其分布函数及密度函数分别为:
其中α>0为形状参数,β>0为尺度参数。

1) 当α>1时,T的数学期望为:
2) 当α>2时,
方差为:
变异系数为:
3) 当α>3时,偏度为:

[Γ(1-3/α)- 3Γ(1-1/α)Γ(1-2/α)+2Γ3(1-1/α)]
4) 当α>4时,峰度为:
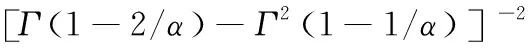
4Γ(1-1/α)Γ(1-3/α)+3Γ2(1-2/α)]-6
Frechet分布变异系数、偏度及峰度函数关于α单调减少,如图1所示。
引理1:记非负随机变量T的密度函数、分布函数及失效率函数分别为f(t),F(t),λ(t),密度函数在(0,+∞)上连续并二阶可导。记g(t)=[1-F(t)]/f(t),η(t)=-f′(t)/f(t),则有结论:若对所有t有η′(t)>0,则λ(t)单调递增。若对所有t有η′(t)<0,则λ(t)单调递减。若η(t)先减后增,即η(t)为“浴盆”曲线,则:
如果存在y0使得g′(y0)=0,则η(t)也为“浴盆”曲线,否则η(t)单调递增。若η(t)先增后减,即η(t)为“倒浴盆”曲线,则:如果存在y0使得g′(y0)=0,则η(t)也为“倒浴盆”曲线,否则η(t)单调递减。
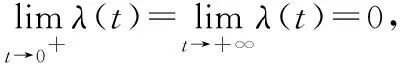
证明:T的失效率函数为
由引理1,有:
故当0
因此存在y0∈(0,+∞),使得λ(y0)>0,故T的失效率函数为“倒浴盆”曲线。
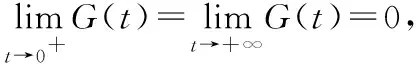
证明:T的平均失效率函数为
则有:
令u=β/t,则G(u)=-u/β·ln(1-e-uα),记h(u)=uln(1-e-uα),则:
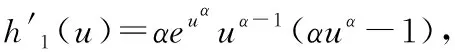
Frechet分布失效率函数和平均失效率函数图像如图2所示,在不同的参数下均呈现“倒浴盆”形状。
1.2 缺失数据寿命分布参数的逆矩估计
在产品寿命试验中,由于试验设备故障以及数据采集过程遗漏等原因,比如数据存储的失败,存储器的损坏,数据录入人员失误漏录等,均会造成试验数据的缺失。较之全样本数据场合下的统计分析,缺失数据只能得到其前后的寿命数据,其统计方法有所不同。缺失数据情形在现实中经常发生,因此对于缺失数据的研究是非常必要的。
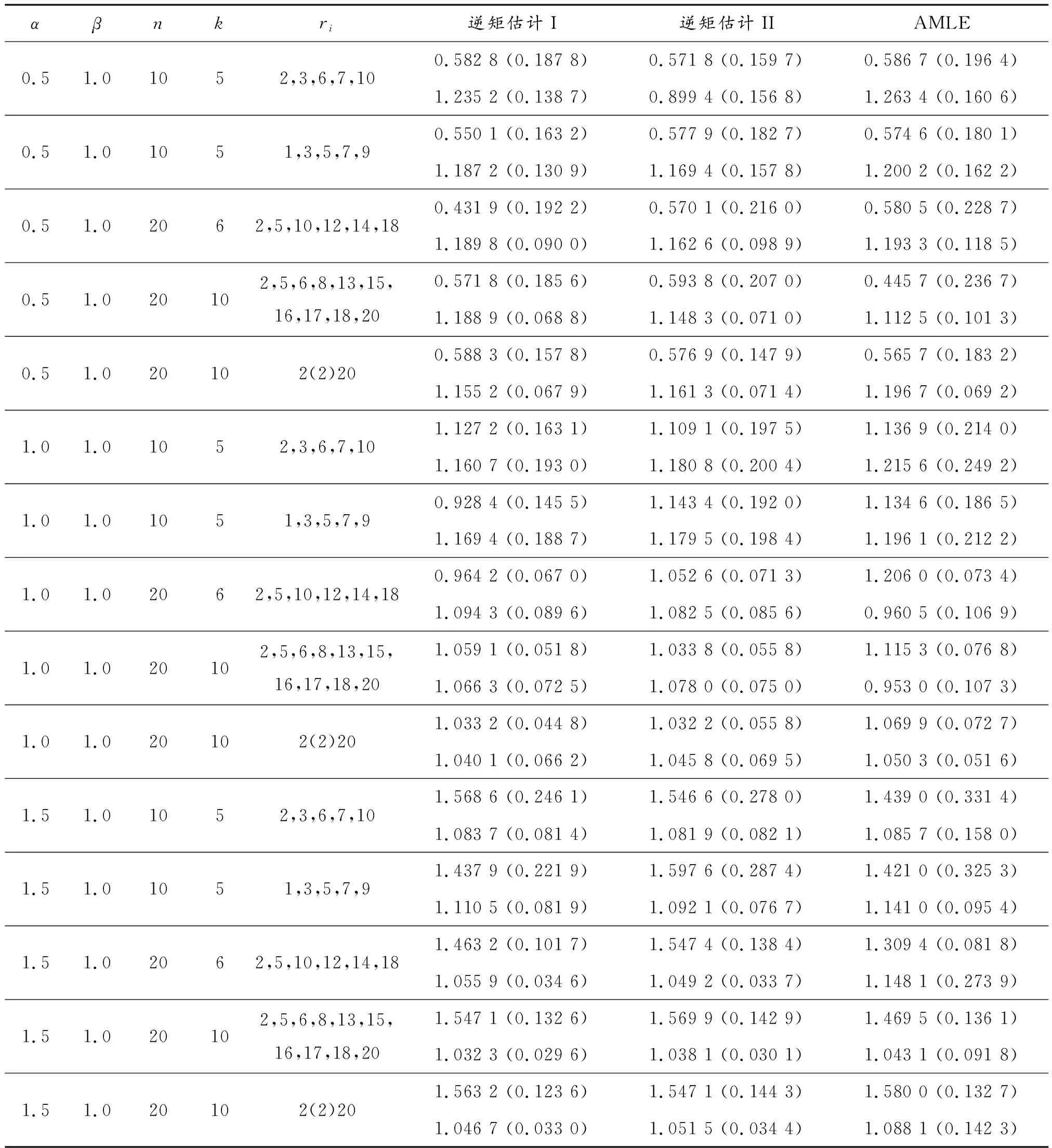
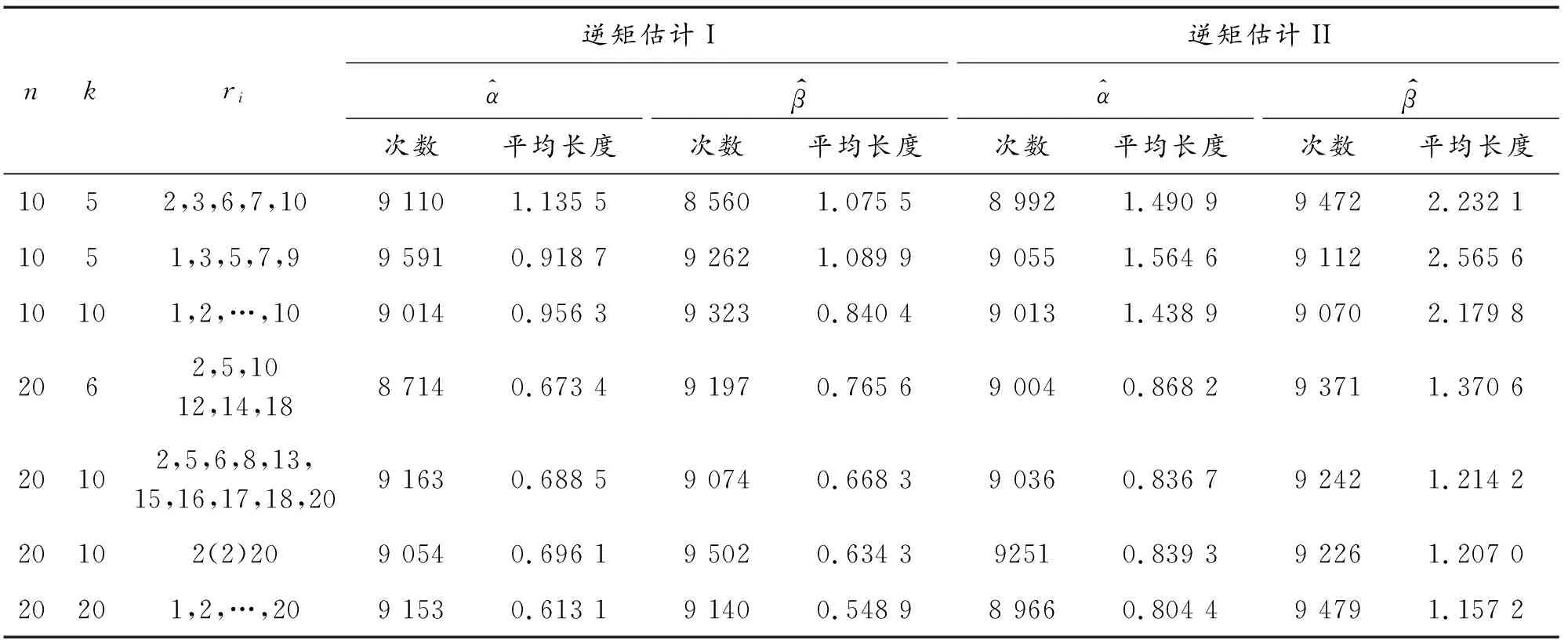
假设有n个产品进行寿命服从Fr(α,β)分布的寿命试验,其次序失效数据为:t(1)≤t(2)≤…≤t(n)。现由于某些原因造成部分数据缺失,剩余的k个数据记为0t(r0) 1.2.1 逆矩估计I 证明:首先有 要证明ln(Sk/Si)单调,则证明函数δ(α)单调即可。对δ(α)求导: 由于T(rk+1-j2) Q1(α)=E1 由引理2可知上述方程有唯一正实根。 针对不同的样本数n,在不同的r1,r2,…,rk下,进行10 000次的Monte-Carlo模拟,将Q1,Q2的分位数、期望及方差汇总至表1。 表1 Q1,Q2的分位数 1.2.2 逆矩估计II 引理3:若随机变量T~Fr(α,β), T(1),T(2),…,T(n)为其前n个次序统计量。序列{ri},i=1,2,…,k满足0 证明:对Q3(α)求导: 所以对于1 Q3(α)=E3 根据引理3可知上述方程的解唯一。 针对不同的样本数n,在不同的r1,r2,…,rk下,进行 10 000次的Monte-Carlo模拟,将Q3,Q4的分位数、期望及方差汇总至表2。 表2 Q3,Q4的分位数 为考察参数估计值的精确性,在不同的数据场合下进行模拟试验。在真值为α=0.5,1.0,1.5,β=1,样本数为n=10,20,不同的缺失数据情形下分别进行5 000次Monte-Carlo模拟试验。对比逆矩估计I、逆矩估计II以及文献[11]中的近似极大似然估计方法估计的结果,模拟结果见表3,括号中的数值表示估计值的均方误差。从表3中可以看出,当样本数为n=20,k=10时,AMLE的结果与逆矩估计I、逆矩估计II的精度近似;当n=20,k=6,即缺失数据较多时,AMLE的点估计误差较大,而且逆矩估计I、逆矩估计II的结果比较满意;当n=10,k=5,即样本数较少、缺失数较多时,两种逆矩估计的均方误差均低于AMLE的均方误差。 对于逆矩估计I及逆矩阵估计II,为考察其区间估计的精度,取真值α=β=1.0,样本数为n=10,20,置信水平为0.90,分别在不同的缺失数据情形下进行10 000次Monte-Carlo模拟试验,得到参数的区间估计,并记录真值落入区间的次数以及区间的平均长度,结果如表4所示。从表4中结果可以看出:逆矩估计I的平均置信区间长度均小于逆矩估计II的平均置信区间长度,且真值落入区间的次数多于逆矩估计II。结合引理3对方程条件有一定限制,故实际应用中应考虑使用逆矩估计I。 表3 Monte-Carlo模拟对比结果 表4 Monte-Carlo模拟的区间估计(置信水平90%下) 算例:取真值为α=β=1.0,样本容量为n=20,ri取2,5,6,8,13,15,16,17,18,20。通过Monte-Carlo方法产生10个服从Frechet的随机数:t(2)=0.391 3,t(5)=0.494 0,t(6)=0.768 9,t(8)=1.143 5,t(13)=3.738 7,t(15)=5.351 6,t(16)=6.443 3,t(17)=8.144 9,t(18)=12.652 8,t(20)=65.408 0。 对两参数Frechet分布在缺失数据场合下提出运用逆矩估计的方法,提出两种不同的逆矩估计方法,对参数进行了点估计以及区间估计,通过Monte-Carlo模拟试验以及算例证明了逆矩估计在均方误差意义上要优于近似极大似然估计,并将两种逆矩估计的方法进行对比,说明逆矩估计I更优。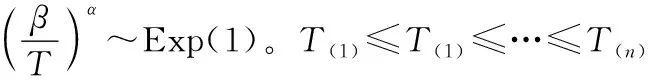
2 Monte-Carlo模拟
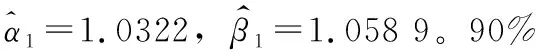
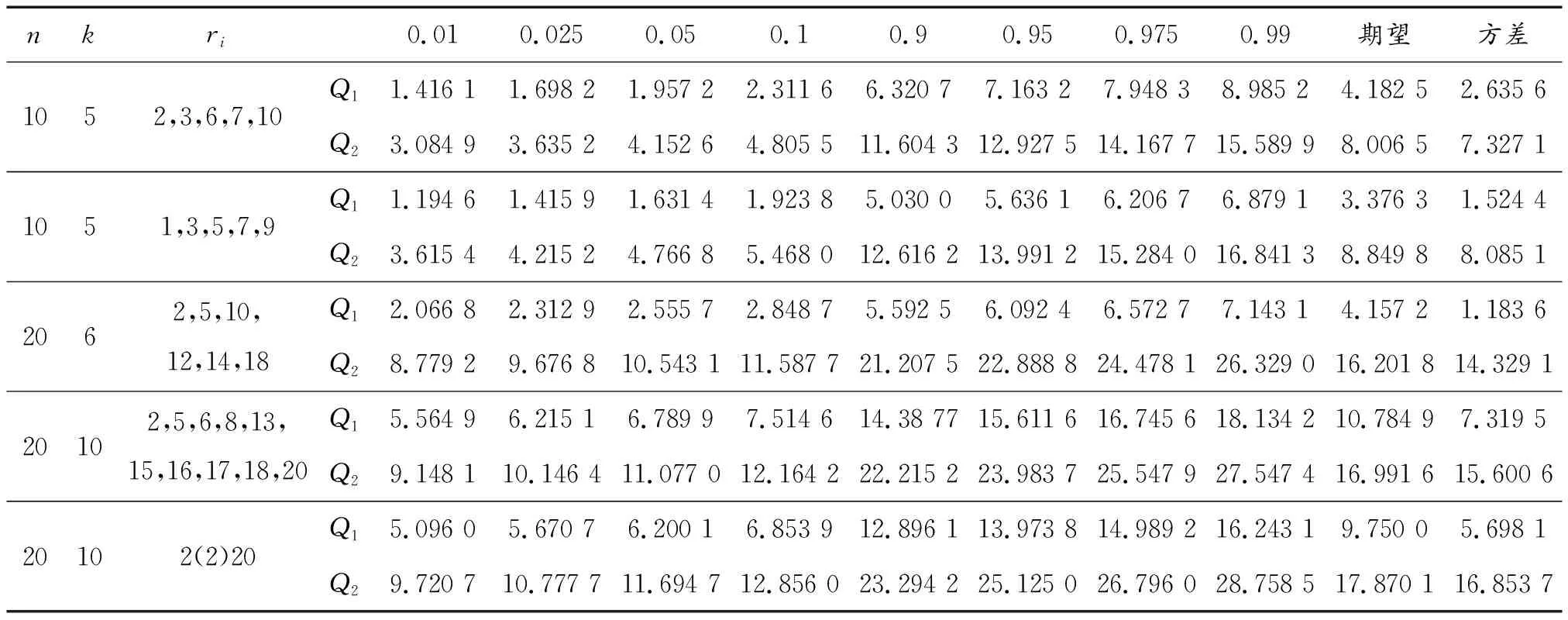
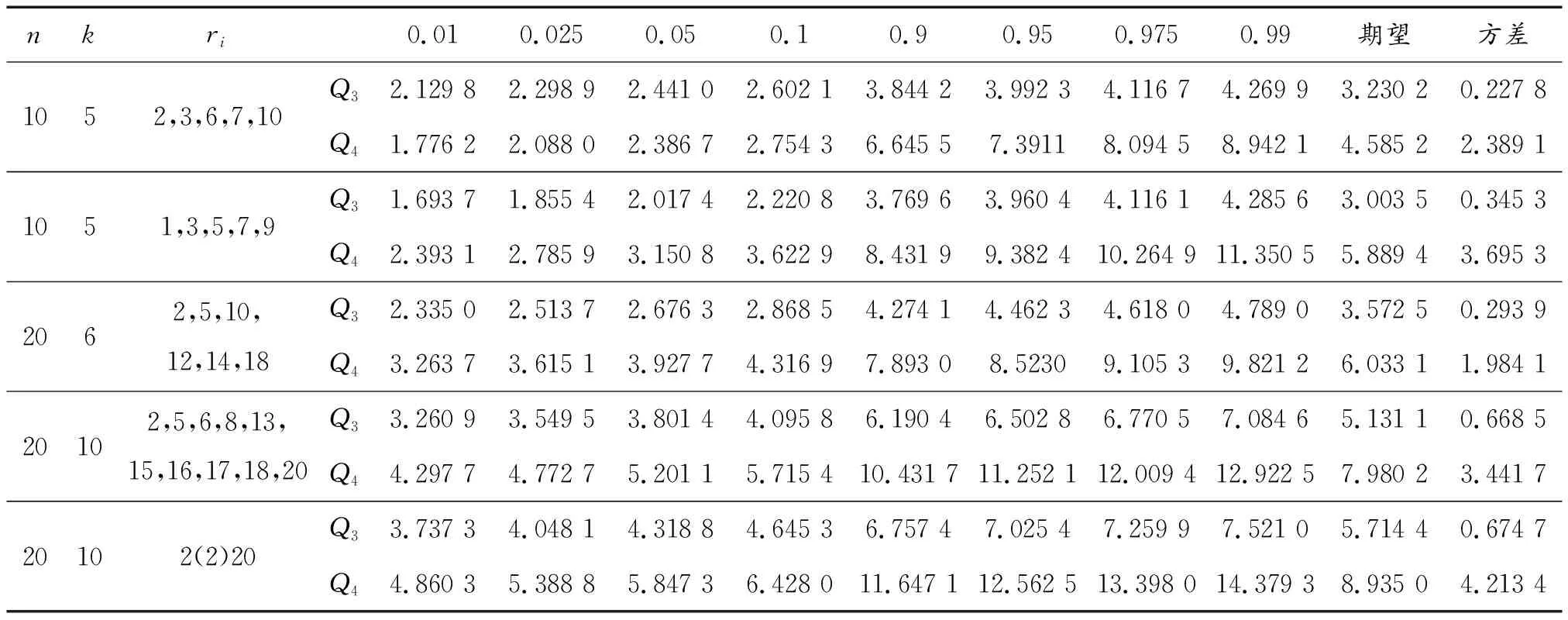
3 结论
