变速变桨距风电机组减载调频综合控制策略研究

严干贵，赵伟哲，张礼珏

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.国网江西省电力有限公司 电力科学研究院，江西 南昌 330000；3.中国电建集团吉林省电力勘测设计院有限公司，吉林 长春 130000)

低碳电力推动风电大规模发展，风电占比显著增加.风电机组输出功率受风速、气压等因素影响，具有随机性、间歇性和波动性等特点.因此，风电并网容量的不断增加给包括电力系统频率稳定性在内的电力系统安全运行问题带来新挑战.众所周知，双馈感应风电机组在风力发电中仍占主导地位[1]，其经变流器接入电网，当风电机组运行于最大功率跟踪(Maximum Power Point Tracking，MPPT)模式下时，风电机组不能响应系统频率变化，对系统惯性无贡献[2]，导致系统整体惯性降低，恶化了系统运行安全性.因此，高风电渗透电力系统的调频问题愈加突出.

提高电力系统频率调节能力的有效途径是配置一定的旋转备用容量.部分国家如挪威[3]、英国[4]、德国[5]等都制定了相应的并网准则，要求风电场需配置足够备用容量以满足系统调频需求.

国内外专家学者在风电机组调频控制策略设计领域做了大量研究.文献[6]首先提出通过模拟同步发电机组惯性，使风电机组可短时响应系统频率调节；文献[7]对于光伏发电系统输出特性进行分析.针对光伏并网发电在遇到频率波动时不具备惯性和调频能力的问题，提出了应用储能补偿系统的调频需求，通过对储能逆变器采用虚拟同步发电机控制策略，使光-储作为一整体对外具备类似同步发电机特性，同时该系统还拥有保证光伏对外输出功率稳定的能力；文献[8]提出通过控制风电机组转子变速运行，使风电机组运行于减载(Deloading Power Point Tracking，DPPT)模式，使之具有可持续向上调节功率空间[9～10].变速法响应速度快、支撑持续时间长，但受上限转速限制，在高风速工况下风电机组可允许变速范围非常有限，所能提供的备用功率支撑也微乎其微；为此，文献[11]提出变速、变桨相协调的减载调频控制策略，在高风速下通过变桨降低机组出力，使机组仍能预留足够备用容量以备系统调频之需，但变桨调节速度慢，易造成机械磨损.

本文设计了双馈感应风电机组减载调频运行模式，基于PSCAD/EMTDC平台，构建变速与变桨协调的减载调频控制策略，分析了不同运行工况下风电机组调频能力的差异性.与此同时，围绕风电机群参与电力系统调频问题，验证了所提出的风电机群调频控制策略的有效性，并且基于实测风速数据分析了风电机群不同减载程度参与调频的经济性.

1 DFIG-WT减载运行曲线

根据风力机风能捕获原理：

(1)

Cp=Cp(β，λ)，

(2)

λ=λ(Vm，ω)，

(3)

最优风能捕获功率为桨距角和转速的函数

Popt=f(βopt，ωopt)，

(4)

式中：ρ为空气密度(kg/m3)；R为叶片半径(m)；Vm为风速(m/s)；Cp为风能捕获系数；λ为叶尖速比；β为桨距角(°)；ω为转子转速，ωmin<ω<ωmax(rpm).因此，可通过“变速法”或“变桨法”调节风力机转速或桨矩角，使其偏离最佳运行点，即可使机组具备“向上”调节功率的能力.次优模式下风力机捕获的风功率可表示为

P=f(βopt+Δβ，ωopt+Δω)

.

(5)

次优模式下，风力机输出功率偏离最大风能捕获功率值越大，机组可释放功率越大.由于不同工况下机组运行约束不同，在设计机组减载水平时，需要考虑具体约束.

机组运行于功率追踪区时通过“变速法”实现减载运行，即

P=f(βopt，ωopt+Δω)，

(6)

其中：Δβ=0°，定桨距运行.

功率恒定区时，受转速极限限制，仅凭变速法难以实现风电机组减载功率的有效调节，需辅之桨距角调节，即

P=f(βopt+Δβ，ωopt+Δω)，

(7)

其中：Δβ≠0°，变桨距运行.

不同风速下机组减载运行曲线，如图1所示.

图1 不同风况下减载运行示意图

图2 风力机MPPT与DPPT运行模式下Pm-ωr曲线

考虑不同风况下的运行约束，可以得到如图2所示的风电机组减载运行曲线.图中ΔP为风电机组减载运行时面对系统频率跌落可释放电磁功率，即风电机组能够参与电力系统向上调频的备用容量.

为确定风电机组参与系统调频所需备用容量ΔP，本文定义机组减载程度del%：

(8)

式中：PN为额定功率，即本文所选功率基准值.

2 减载调频运行控制策略

根据风力机减载运行曲线，协调转子侧变流器对发电机的变速控制和风力机桨距角控制，以实现风电机组的减载运行控制.

2.1 减载运行控制策略

在根据风力机的运行曲线确定转子运行曲线，当参考力矩、参考无功功率给定后，求得相应的参考转子电流，进而控制转子侧变流器产生相应转子电压，实现发电机组的转速调节.“变速法”通过降低输出功率参考值，使风电机组变速减载运行，控制原理如图3所示.

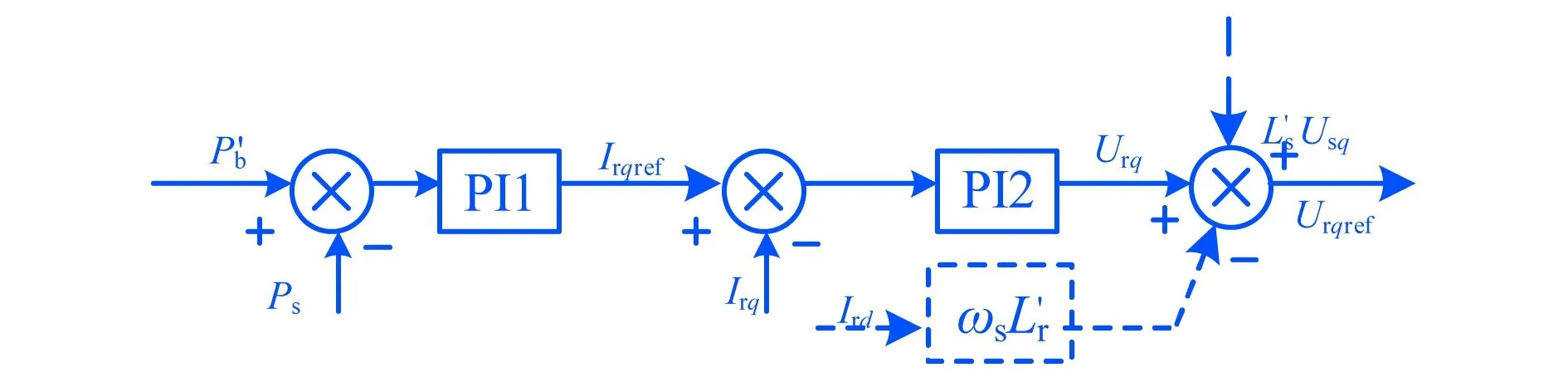
图3 “变速法”发电功率控制策略

图4 “变桨法”控制策略

图5 同步发电机组调速器控制框图

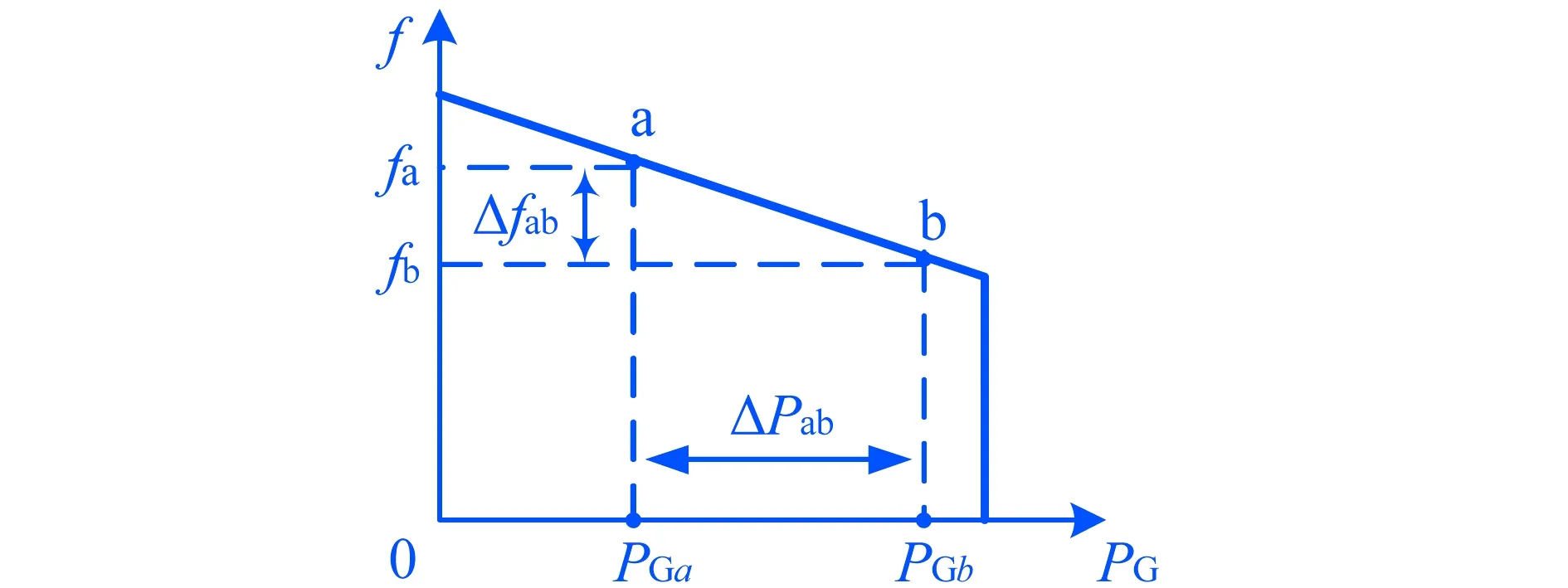
图6 同步发电机组下垂控制特性曲线

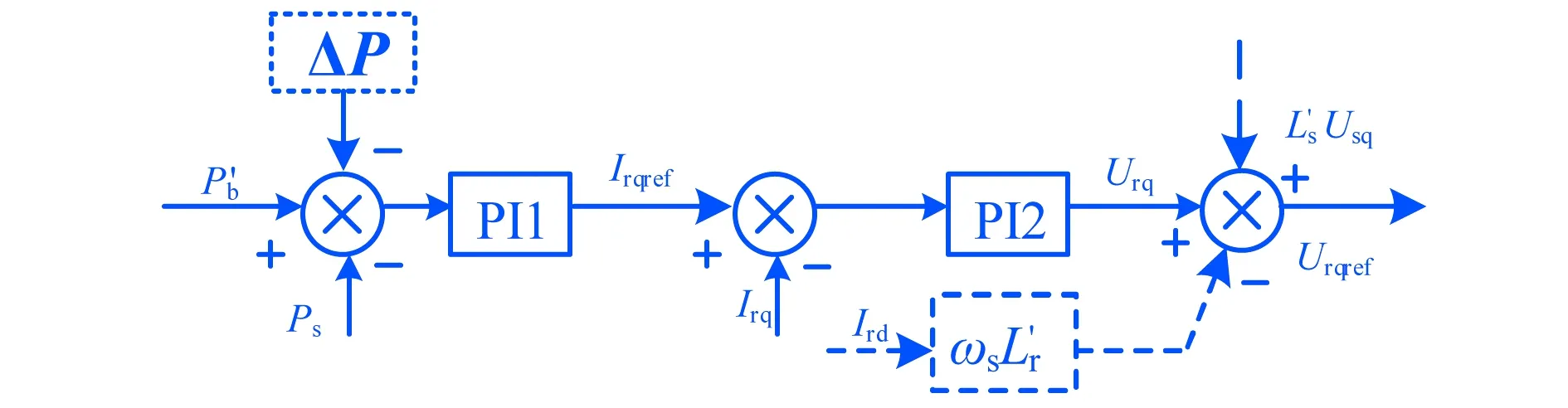
图7 频率响应下垂控制器

图8 减载调频综合控制策略

当“变速法”动作后，转子转速或风功率超过其极限值时，桨距角控制器动作，增加风力机桨距角，降低风力机机械输出功率[9]，如图4所示.

图4中，ωr为发电机实际转速；ωref为发电机转速参考值；β、βref为桨距角运行值与参考值；βmax、βmin为桨距角最大值与最小值；max-rate、min-rate为桨距角变化率上限和下限.max表示取两输入信号大者，确保转速超过最大值时桨距角控制动作.此时“粗调”桨距角，限制发电机转速越限，保持风电机组输出功率恒定.

2.2 调频控制策略

传统电力系统中，常规同步发电机组发展相对于新能源发电技术较为成熟，具有良好的稳定性，调频性能出色.本文通过分析借鉴同步发电机调频机制，设计DFIG频率响应控制器，使其模拟同步发电机下垂特性，响应系统频率变化.

对于同步发电机组，转子转速与系统频率相耦合，系统有功功率缺失引起频率跌落，诱发同步发电机转速下降，释放转子动能，阻尼频率跌落.一段时间过后，调速器动作，其控制框图，如图5所示.

图5中，ωr为同步发电机转速；ω0为机租参考转速；Kp为增益值；σ为同步发电机组调差系数；ΔY为涡轮机阀门改变量.

涡轮机阀门位置的改变，增加了发电机由机械功率到电磁功率的转化量，发电机有功输出增加，响应系统频率变化.同步发电机有功输出随系统频率下降而增发的特性称为下垂特性，如图6所示.

图6中,fa、fb和Δfab分别为a、b状态下系统频率及对应的系统频率变化量；PGa、PGb和ΔPab分别为a、b状态下发电机组有功出力及对应的有功出力变化量.

DFIG频率响应控制器，如图7所示.其中机组有功输出增发量ΔP是系统频率偏差的K倍，即

ΔP=Δf·K=(fsys-fn)·K，

(9)

式中：fsys为系统频率(Hz)；fn为额定频率(Hz)；K为频率调整系数.

频率控制器动作后，转子转速下降，迅速释放动能，同时桨距角参考值变化，触发桨距角控制器再次动作，桨距角下降，电磁功率增大.电磁功率增大的同时，为维持转子运动平衡，机械功率沿风功率曲线逐渐上升，最终达到功率平衡.

本文设计减载调频综合控制策略，如图8所示.

下垂控制调频效果等同于同步发电机的一次调频，即成比例的有差调节，该调节过程作用时间短，动作速度快，在风电机组参与系统调频控制中广泛采用.

3 仿真分析

基于PSCAD建立850 kW双馈感应风力发电系统，设计了不同风速下风电机组减载运行算例，对所提出控制策略有效性进行验证.仿真结果中功率、转速皆为标幺值，选取风电机组基本容量为基准值，PB=PN=850 kW.转子转速最大值为1 900(rad/min)，本文所选转速基准值为1 500(rad/min)，转速极限值为1.27(p.u.).

3.1 减载控制仿真分析

本文设计不同运行工况下减载控制策略，其关键在于低、中、高风速下桨距角是否动作、如何动作.因此首先通过仿真分析验证不同运行工况下减载控制策略设计合理正确，根据风电机组物理运行约束确定减载约束条件，从而得到不同风速下减载能力.

3.1.1 减载方法验证

取功率追踪区、功率恒定区时不同风速8 m/s、11 m/s、13 m/s进行仿真分析，5 s时降低有功功率参考值“Pb”，比较不同风速下桨距角、转速及电磁功率变化情况，仿真结果如图9所示.

(a)Vw=8 m/s (b)Vw=11 m/s (c)Vw=13 m/s图9 不同风速下DFIG减载运行仿真曲线

图9给出了不同工况机组减载运行时桨距角β、转子转速ωr及电磁功率Pe的动态响应曲线.低风速下，桨距角不动作，转速明显增大，电磁功率由0.32跌落至0.28，系统稳定运行，风电机组通过“变速法”实现6%减载运行；中、高风速下，桨距角及转子转速均明显增大，电磁功率跌落，风电机组通过“变速法”与“变桨法”协调控制实现减载运行.其中，中风速下减载幅度9%，高风速下减载幅度7%.

3.1.2 确定减载能力

为进一步验证该减载控制策略对风电机组功率跌落的幅度影响，本文通过给定不同有功功率参考值(即不同ΔPb)，根据风电机组状态量的变化情况，分析其减载运行物理约束，并得到不同运行工况下减载能力.

风速分别在8 m/s、11 m/s下，5 s时分别降低ΔPb=0.1及ΔPb=0.2，仿真结果如图10、图11所示.

图10 不同ΔPb下仿真结果(功率追踪区)图11 不同ΔPb下仿真结果(功率恒定区)

图10、图11对比了不同ΔPb下风电机组受减载控制后桨距角β、转子转速ωr及电磁功率Pe的响应特性.由仿真结果可知，不同工况下，随着ΔPb增加：桨距角动作幅度增大(低风速下不动作)；转子转速上升幅度增大；电磁功率跌落幅度增大，即减载能力更强.但若继续增大ΔPb，仿真结果如图12所示，转子转速易超过其极限值；电磁功率大幅波动，影响风电机组运行稳定性.

(a)Vw=11 m/s (b)Vw=13 m/s图12 ΔPb过大时仿真结果

因此，功率恒定区，减载幅度受转速极限值及运行稳定性限制；在低风速下，转速不会越限，但其可减载幅度很小.根据转速极限以及功率稳定约束，可近似得到不同风速区间内ΔPb的范围，如表1所示.功率追踪区域内转速不会越限，ΔPb最大；随风速逐渐增大，ΔPb有所减小.

表1 不同风速范围下ΔPb取值

结合不同风速下运行约束条件，可得到各运行工况下的仿真结果，如表2所示.不同风速下减载前后功率曲线图，如图13所示.

表2 不同风速下可减载功率仿真结果

图13 不同风速下减载前后功率曲线图

结合表3和图13，显而易见，风电机组在中等风速下时减载能力最强.

3.2 调频控制仿真分析

中等风速下减载幅度最大，以中等风速为例分析调频控制的有效性.风速为11 m/s，3 s加入减载控制模块，增大转速，使之减载运行；减载运行稳定一段时间后，9 s系统功率跌落至49 Hz，仿真结果如图14所示.

仿真结果表明，当系统频率下跌时，风电机组频率控制环节动作，转速下降，释放动能，同时桨距角变小，风电机组输出机械功率增大，实现风电机组参与系统调频.该仿真结果说明本文所设计减载调频控制策略能够在系统频率波动时提有功支撑，响应系统频率变化.

图14 系统频率跌落时风电机组动态响应仿真结果

图15 相同减载与最大减载容量对比

图16 各发电机组最大可减载程度图

图17 风电场不同运行模式下全天发电量对比图

3.3 两台机组优化减载仿真分析

不同风场同一时间风况不同，同一风场不同风机之间的风况也存在差异.当需要风机参与调频时，若各风机减载水平相同，平均分配减载功率必然存在不合理性.所以，根据不同风况为各风场乃至各风机下派调频任务变得尤为重要.

本文以风速为8 m/s及11 m/s的两台850 kW风电机组为例.根据本文仿真分析，8 m/s风速下风电机组最大减载幅度为6.82%，即可减载功率为58.0 kW.11 m/s风速下风电机组最大减载幅度为10.35%，即可减载功率为88.0 kW.需要该两台机组共同完成146 kW减载任务，如若不按照各自减载能力分配减载任务，而是平均分配需减载功率，即各自承担73 kW，则此二台机组运行情况如图15所示.

从仿真结果可知，若按照平均分配需减载功率的原则(图中蓝色曲线)，在低风速下桨距角动作，频繁变桨将降低风机使用寿命；中风速下并未充分利用可减载功率，风电机组运行效率较低.根据本文设计的减载原则(图中绿色曲线)，可在不同风速下充分利用各风电机组调频功率，又可避免频繁变桨对风机造成的机械磨损.

3.4 风电场减载运行经济性分析

前文写到，为了应对风功率不可预测性，德国电网导则要求风电场保留其总装机容量的9%作为功率备用.本文以东北地区某风电场实测风速数据为例，该风电场装配64台G58-850 kW双馈感应风力发电机组.结合仿真结论，得出图16.

结果表明，风场内各风电机组最大可下调功率受当前风况制约，最大减载程度仅为装机容量3.59%，不切机情况下减载水平与德国电网导则要求相去甚远.

另一方面，风电场长期弃风减载导致风能极大的浪费.以1天风速采样数据为例，采样周期为1分钟.分别对比分析风电场最大功率追踪运行模式下全天发电量，减载9%风电场全天发电量以及仿真所得最大减载程度发电量，如图17所示.

以全天最大功率追踪模式运行下的发电量(318.62 MW·h)为基准，可以看出，恒定减载9%(201.12 MW·h)较本文测得最大减载程度发电量(279.63 MW·h)多损失24.64%发电量.

至此，恒定减载水平容易造成风电场发电量大规模浪费.采用本文设计方法，系统频率跌落时风电场有能力提供一定有功支撑的前提下，降低了风电场弃风量，提高了风电场经济性.

4 结 论

本文围绕风电机组参与系统调频问题，设计了一种基于“变速”和“变桨”协调控制的减载调频控制策略，通过理论和仿真分析得到如下结论：

(1)根据不同运行工况下的物理约束条件，整定出具备向上调节能力的初始运行点.

(2)不同风速下减载调频策略、对风机运行的约束条件及减载能力不同，低风速下受有功输出限制，减载能力低，仅需“变速法”便可实现减载运行；中风速下其转速变动幅度大，因此其减载能力最强，需采用“变速法”和“间接变桨法”实现减载；高风速下，其转速已接近额定值，调节范围小，且受风电机组运行稳定性限制，减载能力低，需采用“变速法”和“间接变桨法”实现减载.

(3)与过去研究成果相比，本文设计减载控制策略只需设定不同风速下最大ΔPb及转子转速极限值，即可将“转速”及“桨距”控制系统灵活切换.

(4)下垂控制对频率响应速度快，可瞬间释放转子动能实现对系统频率的支撑.

(5)按风电机组运行工况优化配置各机组减载任务，可提高多机调频效能，减少资源浪费.