粒子群算法修正测距的 无线传感器网络节点定位

楼国红, 张剑平

(太原工业学院 电子工程系, 太原 030008)

无线传感器网络由自治无线节点构成, 这些节点随机部署在一个区域, 对控制对象的参数进行收集, 如温度、 声音、 电压等, 以帮助管理人员快速、 及时地收集对象数据. 节点定位是无线传感器网络的应用基础, 如果节点位置信息无效或错误, 则无线传感器网络无法对目标进行准确、 实时监控, 因此节点定位方法的设计与研究是该领域关注的焦点[1-3].

目前, 节点定位常采用全球定位系统(global positioning system, GPS)对节点的位置进行计算, 该方法受外界环境干扰小、 实时性好、 鲁棒性高, 是目前定位精度最高的一种方法[4]. 无线传感器网络由大量的节点组成, 如果每个节点安装一个GPS, 会导致无线传感器网络定位的成本高, 因此通常对少量的无线传感器网络节点安装GPS, 其位置已知, 这些节点称为锚节点[5]. 先将锚节点的位置作为参考信息, 再对其他未知节点的位置进行估计和定位, 当前无线传感器网络节点定位算法根据是否需要硬件支撑情况划分为两类： 测距的无线传感器网络定位算法和无需测距的无线传感器网络定位算法[6]. 测距的无线传感器网络定位算法需要额外硬件支持, 根据信号强度或角度信息对无线传感器网络的节点位置进行估计, 如基于信号接收强度指示的无线传感器网络定位算法, 其传感器节点定位精度高, 定位成本也相对更高. 而无需测距的无线传感器网络定位算法不需要额外硬件支持, 工作过程相对简单, 已成为当前无线传感器网络的主要研究方向[7-9]. 无需测距的无线传感器网络定位算法主要有质心定位算法和DV-Hop算法. 质心定位算法根据无线传感器网络的连通性和未知节点不断接收到的锚节点发送信息进行定位, 但其定位误差较大, 无法准确确定未知节点的位置. 为了解决质心定位算法的缺陷, 文献[10-12]将测距中的到达时间差定位算法与其进行组合, 对其定位结果进行加权, 一定程度上提高了节点的定位精度, 但权值如何进行确定没有统一的标准和理论指导, 定位结果并非真正的最优. DV-Hop定位算法根据锚节点与未知节点之间的跳距实现节点定位, 因此节点距离的估计最关键, 标准DV-Hop定位算法采用平均距离作为节点距离, 当无线传感器节点的分布不均匀时, 测距值估计的距离较大, 从而导致传感器节点的定位误差较大. 文献[13]提出了采用遗传算法对测距进行优化和修正, 减少平均测距误差, 但遗传算法存在收敛速度慢, 进化后期易出现停滞现象, 难得到局部最优解, 对测距优化结果产生不利影响, 最终对无线传感器网络的节点定位结果进行干扰.

针对节点定位存在的问题, 本文设计一种基于粒子群修正测距的无线传感器节点定位算法. 首先对DV-Hop的工作原理进行分析, 找到导致跳距估计误差的因素, 然后采用粒子群算法对无线传感器节点之间的测距估计结果进行修正, 以减少节点间的测距估计误差, 并对标准粒子群算法的不足进行相应的改进, 最后通过仿真实验与当前经典无线传感器节点定位算法进行对比测试. 测试结果表明, 在相同工作环境下, 本文方法提高了无线传感器节点的定位精度, 且未增加额外硬件开销, 比经典无线传感器节点的整体定位性能更优.

1 无线传感器网络结构

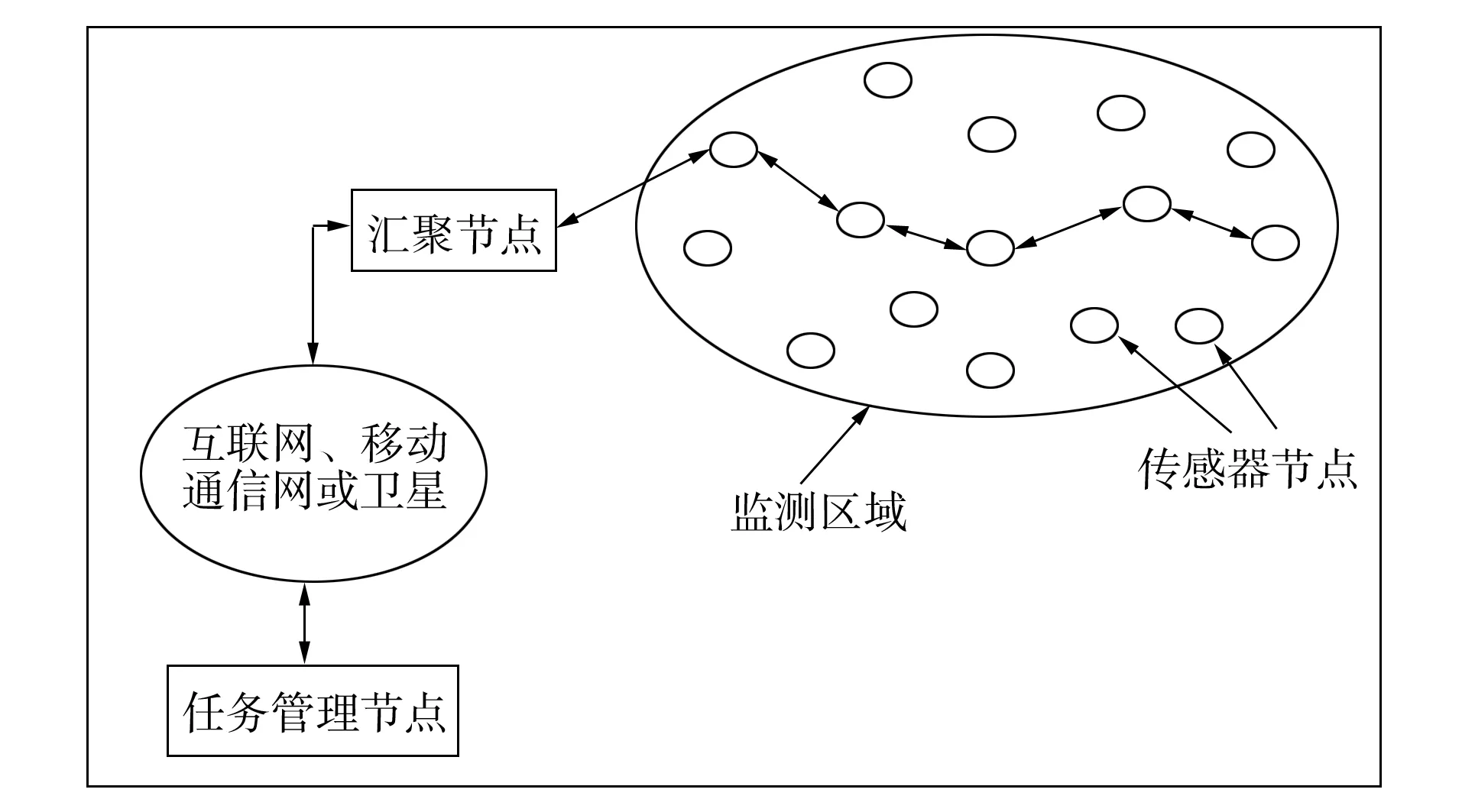
图1 无线传感器网络的基本结构Fig.1 Basic structure of wireless sensor networks

无线传感器网络常包含大量的节点, 节点采用随机方式进行部署, 分布极不均匀, 单个节点的数据处理和存储能力有限, 因此节点之间信息冗余较高, 这些节点自动构成一个无线网络, 对监测对象信息进行采集, 通过与相邻节点之间的信息转发方式将信息发送到汇聚节点, 汇聚节点主要负责数据的融合, 然后将数据发送到移动通信网络, 移动通信网络将数据发送到需要的用户. 在整个网络中, 每个节点均有一个用于识别的号码, 普通节点的能量通常有限, 且不能进行补充, 而汇聚节点的能量是无限的, 不受限制, 而且节点的位置固定不能移动, 其基本结构[14]如图1所示.

2 DV-Hop算法和粒子群算法

2.1 DV-Hop算法

传感器网络有两类节点, 其中一类节点获得自己所在位置坐标的锚节点, 另一类节点不知道自己位置的节点, 只能通过锚节点估计其位置, 称为未知节点. DV-Hop算法是一种根据路由的跳数实现未知节点定位的经典算法, 且节点定位的成本低, 自适应能力强, 步骤如下：

1) 传感器节点之间的最小跳数计算. 每个锚节点在自己通信范围内不断广播自己的位置信息, 收到信息的节点保留最小跳数, 同时对邻居节点进行广播, 这样全部节点都会记录与所有锚节点之间的最小跳数.

2) 计算无线传感器网络两个锚节点之间的平均跳距. 根据锚节点的位置信息和最小跳数可得到任意两个锚节点i和j之间的平均跳距, 计算公式为

(1)

式中:hi,j表示锚节点i和j之间的最小跳数； (xi,yi)和(xj,yj)分别表示锚节点i和j的位置坐标.

3) 未知节点位置的估计. 根据未知节点u和锚节点i之间的最小跳数tu,s及平均跳距可得到未知节点u和锚节点i之间的距离为

du,s=HopSize×tu,s.

(2)

4) 当未知节点得到附近3个锚节点的距离值时, 可采用三边定位算法得到未知节点的位置. 设D为待定位传感器节点,A,B,C为锚节点, 其位置分别为(xA,yA),(xB,yB),(xC,yC), 则可建立如下关系式：

(3)

式中: (x,y)表示D的位置坐标;dA,dB和dC表示节点D与锚节点A,B,C之间的距离.

三边定位算法只利用3个节点的位置信息, 提供的信息有限, 因此可引入极大似然估计法对未知节点的坐标信息进行估计. 设共有n个锚节点, 节点D与其距离分别为di(i=1,2,…,n), 则可建立如下方程：

(4)

对式(4)进行变换和简化后, 可得:

(5)

设

可建立线性方程Ax=b, 从而得

x=(ATA)-1ATb.

(6)

采用最小二乘法, 根据式(6)可得到未知节点D的位置坐标.

对DV-Hop算法的实现过程进行分析可知, 测距决定了无线传感器网络节点的定位精度, 通常情况下, 根据信号强度对测距进行估计. 设节点发射功率为Pt, 发射节点和接收节点之间的距离为d,λ表示发射波长, 则接收节点收到的信号功率为

(7)

式中:Gt和Gr分别表示发射节点和接收节点的增益;L表示功率损耗常数.

可将式(7)得到的信号功率转换为传感器节点之间的实际距离, 但在实际应用中, 由于受空气、 树木及建筑物等外界因素的影响, 根据信号强度得到测距值与实际距离值之间存在一定的偏差, 从而导致节点定位误差, 因此本文引入粒子群算法对测距进行修正.

2.2 粒子群算法

设粒子i的位置向量和速度向量分别为Xi=(xi1,xi2,…,xiD)和Vi=(vi1,vi2,…,viD), 其当前的最优位置和粒子群的当前最优位置分别为Pi=(pi1,pi2,…,piD)和Pg=(pg1,pg2,…,pgD), 则第(k+1)时刻, 粒子i的速度和位置变化公式为

式中相关参数的意义见文献[15]. 惯性权重ω的线性迭代表达式为

(10)

当前的最优位置及粒子群当前最优位置的更新公式分别为

(11)

f(Pg)=min{f(Pi)}.

(12)

标准粒子群算法也存在易出现局部最优解的缺陷, 因此本文引入混沌机制对粒子的位置进行扰动, 帮助其逃离局部最优解. Logistic混沌系统为

zi+1=μzi(1-zi),zi∈[0,1],μ∈(2,4].

(13)

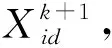
选择遗传算法作为对比算法, 其对式(14),(15)的求解目标函数值变化曲线如图2所示. 由图2可见, 粒子群算法的收敛速度明显快于遗传算法, 目标函数值更理想, 对比结果说明了粒子群算法的优越性.

图2 两种算法对目标函数的求解曲线Fig.2 Solving curves of objective function by two algorithms

3 算法设计

3.1 误差修正系数

为了降低测距误差, 引入距离误差修正系数μ对未知节点潜在的区域进行限制, 以提高无线传感器网络测距的准确性. 距离误差修正系数μ的求解步骤如下:

1) 采用信号强度技术估计未知节点D与m个锚节点之间的距离di(i=1,2,…,m);

2) 随机选择3个锚节点作为参考节点, 得到D的位置约为(x′,y′)；

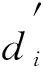
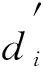
(16)

5) 将ei的平均值作为距离误差修正系数：

(17)

6) 未知节点可行域范围的约束条件为

(18)

3.2 节点定位数学模型

节点定位的数学模型可采用如下形式进行描述：

(19)

无线传感器网络节点定位的目标函数为

(20)

其中M表示距离误差惩罚因子.

3.3 粒子群算法修正测距的无线传感器节点定位步骤

1) 初始化粒子群算法的参数, 如惯性权重、 最大迭代次数;

2) 计算无线传感器网络节点定位的μ, 并确定目标函数;

3) 初始化粒子群的种群;

4) 根据目标函数计算每个粒子的适应度值, 并确定Pi和Pg;

5) 迭代次数增加, 更新惯性权重, 并更新每个粒子的位置和速度, 产生新一代的粒子群;

6) 计算新一代粒子群的适应度值, 并对Pi和Pg进行更新;

7) 如果当前迭代次数超过最大迭代次数, 则得到无线传感器节点的位置.

粒子群算法修正测距的无线传感器节点定位流程如图3所示.

图3 粒子群算法修正测距的无线传感器节点定位流程Fig.3 Flow chart of ranging distance modified by particle swarm algorithm for wireless sensor nodes location

4 仿真测试

选择DV-Hop算法、 遗传算法修正测距的无线传感器节点定位算法在相同实验环境下进行仿真对比实验. 采用VC++6.0进行编程实现定位算法. 定位结果采用如下定位误差进行分析：

(21)

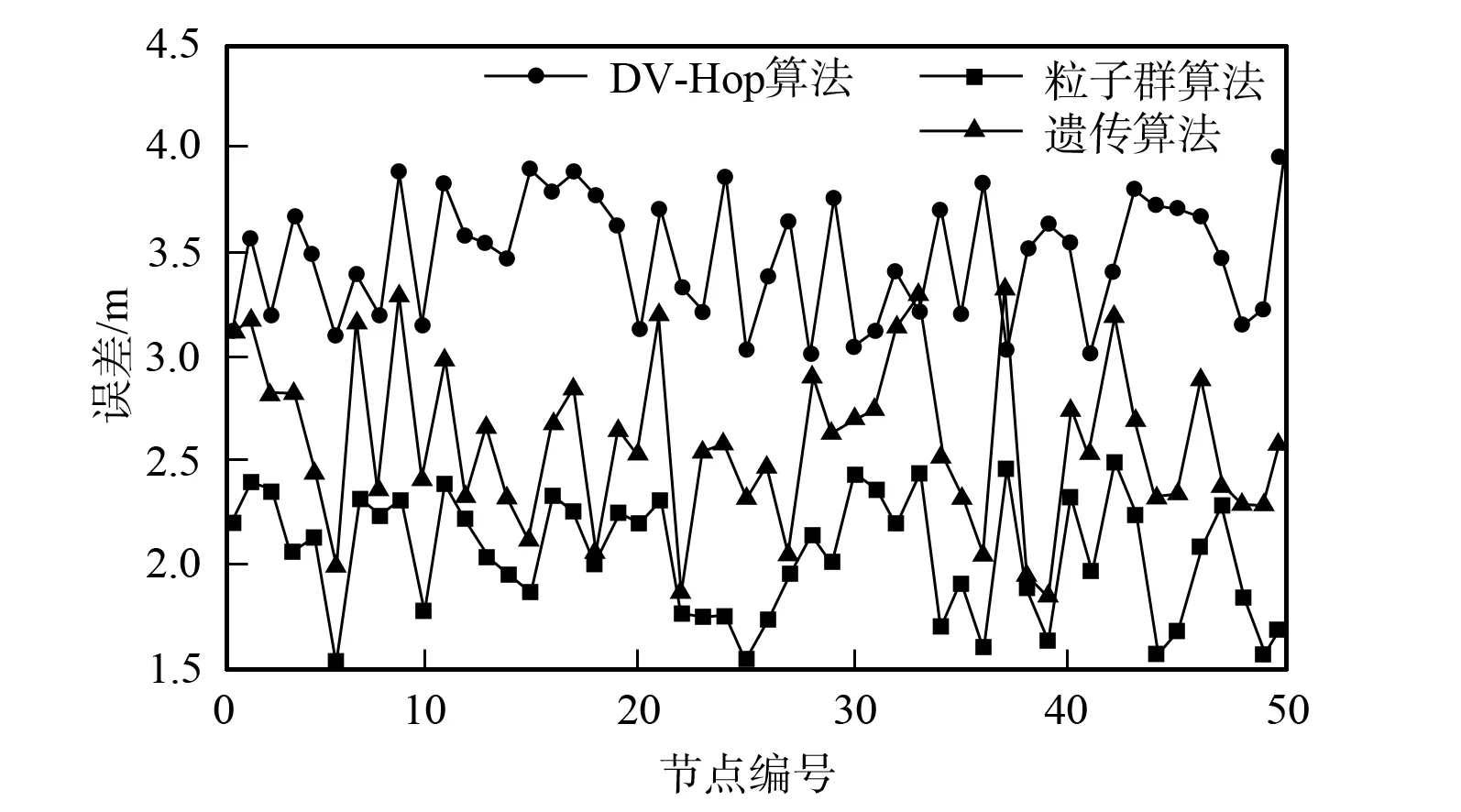
图4 不同算法的传感器节点定位误差变化曲线Fig.4 Location error variation curves of sensor nodes for different algorithms

统计DV-Hop算法、 遗传算法修正测距的无线传感器节点定位算法和粒子群算法修正测距的无线传感器节点定位算法的节点定位误差(m), 结果如图4所示. 由图4可见, DV-Hop算法的节点定位误差最大, 其次为遗传算法, 而粒子群算法修正测距的无线传感器节点定位效果最优.

为了分析不同算法的传感器节点定位实际效果,图5给出了DV-Hop算法(A)、 遗传算法修正测距的无线传感器节点定位算法(B)和粒子群算法修正测距的无线传感器节点定位算法(C)的节点定位结果. 由图5可见, 由于遗传算法和粒子群算法对无线传感器节点的测距误差进行了校正, 因此无线传感器节点定位效果优于传统的DV-Hop算法, 同时粒子群算法定位效果优于遗传算法, 这主要是粒子群算法克服了遗传算法收敛速度慢、 易陷入局部最优的缺陷, 提高了无线传感器节点定位精度.

图5 不同算法的节点实际定位结果Fig.5 Actual location results of the nodes for different algorithms

综上所述, 本文提出了一种粒子群修正跳距的传感器节点定位算法, 仿真测试结果表明, 粒子群算法可解决当前DV-Hop算法定位过程存在的问题, 在不增加额外硬件的情况下, 有效改善了传感器节点定位的效果, 具有一定的优越性.