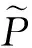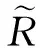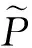Kolmogorov系统的可积性与不可积性

2018-11-06崔美虹张艳妮

吉林大学学报（理学版） 2018年3期

崔美虹, 周冉, 张艳妮

(1. 吉林大学数学学院, 长春 130012; 2. 吉林建筑大学城建学院, 长春 130114)

目前, 关于微分动力系统的动力学行为及可积性等定性性质的研究已有很多结果[1-5]. 本文主要考虑如下Kolmogorov系统:

(1)

如果一个动力系统有足够多的首次积分或不变量, 使得其通解可以通积分(包括隐函数)求解, 则称该动力系统是完全可积的. 如果系统(1)在U上有(n-1)个函数独立的首次积分, 则称系统(1)在U上是完全可积的. 如果H沿着系统(1)的解曲线恒为常值, 或等价地

(2)

记

Mk={(x1,…,xn)∈U|xk+1=…=xn=0},k=1,2,…,n-1.

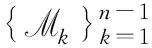
(3)

易见系统(3)是一个k维的Kolmogorov系统, 且是系统(1)的一个子系统, 即如果(x1(t),…,xk(t))是系统(3)的一个解, 则(x1(t),…,xk(t),0,…,0)是系统(1)的一个解. 因此系统(1)完全可积时系统(3)也完全可积.

定理1若Kolmogorov系统(1)于U上解析完全可积, 即存在(n-1)个独立函数解析首次积分, 则对∀k∈{1,2,…,n-1}, 系统(3)在U∩Mk上也解析完全可积.

证明：设Φ1(x1,…,xn),…,Φn-1(x1,…,xn)为系统(1)在U上的(n-1)个函数独立的解析首次积分, 则

在U的一个开稠密子集上是满秩的, 从而在U∩Mk上的一个开稠子集上仍是满秩的, 进而有

(4)

于U∩Mk上的秩≥k-1.

另一方面, 由于M(x1,…,xn)的秩≤k, 即M(x1,…,xn)的秩=k或k-1. 如果M(x1,…,xn)的秩恒为k, 则系统(3)有k个函数独立的首次积分. 不失一般性, 设Φ1,…,Φk满足Φ1(x1,…,xk,0,…,0),…,Φk(x1,…,xk,0,…,0)于U∩Mk上函数独立, 即f1=…=fk恒为0, 从而系统(3)完全可积. 如果M(x1,…,xn)的秩恒为k-1. 类似于上述分析, 可知系统(3)有(k-1)个独立解析首次积分, 从而也完全可积.

由定理1可知, 对n维Kolmogorov系统(1)的可积性研究可简化为对低维问题的研究. 考虑如下一类二维Kolmogorov系统:

(5)

其中: (x,y)∈2;Pn,Qn为两个n次齐次多项式,Rm,Tm为两个m次齐次多项式, 且1≤n

关于这种类型的Kolmogorov系统的Liouville可积性研究可参见文献[9,13], 本文进一步考虑系统(5)的解析可积性与多项式可积性.

定理21) 若系统(5)是解析可积的, 则存在一个齐次多项式H(x,y)及一个齐次有理函数Q(x,y), 使得

(6)

2) 若Pn=Qn不恒为0, 则系统(5)不是解析可积的;

3) 若Rm=Tm不恒为0, 则系统(5)不是多项式可积的.

证明： 1) 设Φ(x,y)是系统(5)的一个非平凡解析首次积分, 将其展开为

Φ(x,y)=Φl(x,y)+Φl+1(x,y)+…,

其中Φk(x,y)为Φ(x,y)的k阶齐次项,Φl(x,y)为最低阶非平凡齐次项, 则有

(7)