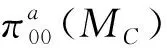2×2上三角算子矩阵的A-Weyl定理的稳定性

赵玲玲, 曹小红

(1. 防灾科技学院 基础教学部, 河北 三河 065201; 2. 陕西师范大学 数学与信息科学学院, 西安 710119)

1 引言与预备知识

令H为复的无限维Hilbert空间,B(H)为H上有界线性算子的全体, K(H)为B(H)中紧算子的全体. 对于T∈B(H), 定义n(T)为零空间N(T)的维数,d(T)为值域R(T)的余维数. 若n(T)<∞且R(T)是闭集, 则称T为上半Fredholm算子; 若d(T)<∞且R(T)是闭集, 则称T为下半Fredholm算子. 如果T∈B(H)是上半(或者下半)Fredholm算子, 则T的指标ind(T)=n(T)-d(T). 若T既是上半Fredholm算子又是下半Fredholm算子, 则称T为Fredholm算子. 算子T的升标asc(T)=inf{n≥0:N(Tn)=N(Tn+1)}, 降标des(T)=inf{n≥0:R(Tn)=R(Tn+1)}. 若算子T是指标为零的Fredholm算子, 则称T为Weyl算子. 若T是升标和降标均有限的Fredholm算子, 则称T为Browder算子. 记ρ(T)为T的预解集,σ(T)=ρ(T)为算子T的谱. 此外, 记σa(T)为算子T的逼近点谱, 且ρa(T)=σa(T). 半Fredholm预解集ρSF(T)、 Weyl谱σw(T)和本质逼近点谱分别定义为:

ρSF(T)={λ∈:T-λI是半Fredholm算子},

σw(T)={λ∈:T-λI不是Weyl算子},

ρe a(T)={λ∈:T-λI是上半Fredholm算子且ind(T-λI)≤0}.

令σSF(T)=ρSF(T),σe a(T)=ρe a(T).

显然,T满足A-Browder定理等价于ρe a(T)=ρab(T), 其中

ρab(T)={λ∈:T-λI为上半Fredholm算子且asc(T-λI)<+∞}[2].

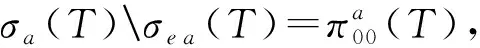
目前, 关于算子矩阵的Weyl型定理的研究已有许多结果[3-6]. 本文考虑2×2上三角矩阵算子满足A-Browder定理和A-Weyl定理微小紧摄动的等价条件.

2 主要结果

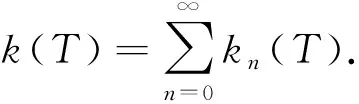
定义3[1]设存在一个非负整数d, 使得当n≥d时kn(T)=0(即当n≥d时, 上述T诱导的映射为同构映射), 则称当n≥d时,T有拓扑一致降标. 当n≥d时, 若R(Tn)在R(Td)的算子值域拓扑中闭, 则称T有拓扑一致降标.

令ρτ(T)={λ∈:T-λI有拓扑一致降标}. 由文献[7]中推论4.9知, 当T为半Fredholm算子时,T有拓扑一致降标. 若T有拓扑一致降标, 则λ是T的一个极点.

下面给出本质逼近点谱的一种变形. 令ρ1(T)={λ∈: dimN(T-λI)<∞, 且存在>0, 使得如果0<|μ-λ|<, 则T-μI是上半Fredholm且ind(T-μI)≤0}, 令σ1(T)=ρ1(T). 显然,σ1(T)⊆σe a(T)⊆σw(T).

若ρτ(T)⊆ρb(T)∪σ1(T), 其中ρb(T)={λ∈:T-λI是Browder算子}, 则对任意的λ∈ρSF(T), ind(T-λI)≥0. 事实上, 令λ∈ρSF(T), 使得ind(T-λI)<0, 则λ∈ρτ(T)σ1(T), 即T-λI是Browder算子. 因此ind(T-λI)=0, 与ind(T-λI)<0矛盾. 对于λ∈ρSF(T),T-λI的最小指标定义为min ind(T-λI)=min{n(T-λI),d(T-λI)}.

引理1令T∈B(H), 则下列叙述等价:

1) 对任意的K∈K(H)且‖K‖<, 存在>0, 使得T+K满足A-Browder定理;

2)T满足A-Browder定理, 且ρSF(T)包含有限多个指标非正的连通分支.

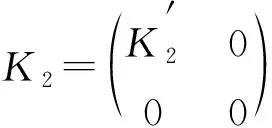
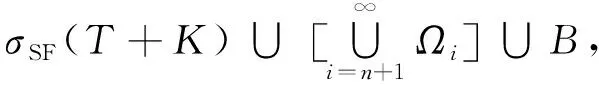
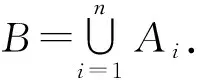
类似引理1的证明, 可得如下引理:

引理2令T∈B(H), 则下列叙述等价:

1) 对任意的K∈K(H),T+K满足A-Browder定理;

2)ρSF(T)仅包含一个指标非正的连通分支.

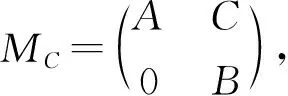
定理1令A∈B(H)使得ρτ(A)⊆ρb(A)∪σ1(A), 则下列叙述等价:

1) 对任意的C∈B(H)及K∈K(H⊕H)且‖K‖<, 存在>0, 使得MC+K满足A-Browder定理;

证明: 1)⟹2). 特别地, 令C=C0, 则2)显然成立.

2)⟹1). 根据引理1, 只需证对任意的C∈B(H),MC满足A-Browder定理, 且ρSF(MC)包含有限多个指标非正的连通分支.

首先证对任意的C∈B(H),MC满足A-Browder定理. 令λ0∈σa(MC)σe a(MC), 则MC-λ0I是上半Fredholm算子, 且ind(MC-λ0I)≤0. 即A-λ0I是上半Fredholm算子, 则λ0∈ρτ(A). 由于ρτ(A)⊆ρb(A)∪σ1(A), 可得ind(A-λ0I)≥0, 因此A-λ0I是Fredholm的, 即B-λ0I是上半Fredholm的. 从而MC0-λ0I是上半Fredholm的, 且

ind(MC0-λ0I)=ind(A-λ0I)+ind(B-λ0I)=ind(MC-λ0I)≤0,

(1)

下证对任意的C∈B(H),ρe a(MC)=ρe a(MC0). 首先证ρe a(MC)⊆ρe a(MC0), 令λ0∈ρe a(MC), 则MC-λ0I是上半Fredholm算子, 且ind(MC-λ0I)≤0, 因此A-λ0I是上半Fredholm的, 由ρτ(A)⊆ρb(A)∪σ1(A), 可得A-λ0I是Fredholm的, 于是B-λ0I是上半Fredholm的, 因此MC0-λ0I是上半Fredholm的, 且式(1)成立, 从而λ0∈ρe a(MC0), 即ρe a(MC)⊆ρe a(MC0). 同理可证ρe a(MC0)⊆ρe a(MC), 于是ρe a(MC)=ρe a(MC0). 由结论(2)和引理1可知,ρSF(MC0)包含有限多个指标非正的连通分支, 因此ρSF(MC)包含有限多个指标非正的连通分支.

根据引理1可得, 对任意的C∈B(H)及K∈K(H⊕H)且‖K‖<, 存在>0, 使得MC+K满足A-Browder定理. 证毕.

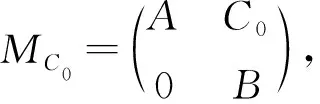
特别地, 在定理1中, 令C0=0, 可得如下推论:

推论1令A∈B(H), 使得ρτ(A)⊆ρb(A)∪σ1(A), 则下列叙述等价:

1) 对任意的C∈B(H)及对所有的K∈K(H⊕H)且‖K‖<, 存在>0, 使得MC+K满足A-Browder定理;

2) 对所有的K∈K(H⊕H)且‖K‖<, 存在>0, 使得M0+K满足A-Browder定理.

根据定理1和引理2的证明, 可以刻画2×2上三角矩阵算子满足A-Browder定理的微小紧摄动.

推论2令A∈B(H), 使得ρτ(A)⊆ρb(A)∪σ1(A), 则下列叙述等价:

1) 对任意的C∈B(H)及所有的K∈K(H⊕H),MC+K满足A-Browder定理;

2) 对所有的K∈K(H⊕H), 存在C0∈B(H), 使得MC0+K满足A-Browder定理.

若isoσa(T)⊆{λ∈: 0

引理3设T∈B(H)为f-a-isoloid, 且acc[isoσa(T)]=Ø, 则下列叙述等价:

1) 对所有的K∈K(H)且‖K‖<, 存在>0, 使得T+K满足A-Weyl定理;

2)T满足A-Weyl定理, 且ρSF(T)包含有限多个指标非正的连通分支.

证明: 利用引理1, 只需证对所有的K∈K(H)且‖K‖<,⊆σa(T+K)σe a(T+K). 由于T满足A-Brwoder定理, 可得⊆acc[isoσa(T)]∪[isoσa(T)], 又由于acc[isoσa(T)]=Ø, 则⊆isoσa(T). 由T为f-a-isoloid且T满足A-Weyl定理, 可得

⊆(σa(T)σe a(T))⊆σa(T+K)σe a(T+K).

因此对任意的K∈K(H)且‖K‖<,T+K满足A-Weyl定理. 证毕.

定理2令A∈B(H), 使得ρτ(A)⊆ρb(A)∪σ1(A),M0∈(H⊕H)为f-a-isoloid且acc[isoσa(M0)]=Ø, 则下列叙述等价:

1) 对任意C∈B(H)及所有的K∈K(H⊕H)且‖K‖<, 存在>0, 使得MC+K满足A-Weyl定理;

2) 对所有K∈K(H⊕H)且‖K‖<, 存在>0且C0∈B(H), 使得MC0+K满足A-Weyl定理.

N(MC-λ0I)⊆(A-λ0I)-1[CN(B-λ0I)]⊕N(B-λ0I),

可得0

1)⟹2). 特别地, 令C=C0, 则2)显然成立.

特别地, 在定理2中, 令C0=0, 可得如下推论:

推论3令A∈B(H)使得ρτ(A)⊆ρb(A)∪σ1(A) ,M0∈(H⊕H)为f-a-isoloid算子, 且acc[isoσa(M0)]=Ø, 则下列叙述等价:

1) 对任意C∈B(H)及所有的K∈K(H⊕H)且‖K‖<, 存在>0, 使得MC+K满足A-Weyl定理;

2) 对所有的K∈K(H⊕H)且‖K‖<, 存在>0, 使得M0+K满足A-Weyl定理.

例2令A,B∈B(l2), 定义A(x1,x2,x3,…)=(x2,x4,x6,…);B(x1,x2,x3,…)=(0,x1,0,x2,0,x3,…). 则: 1)σ1(A)=σ(A), 从而ρτ(A)⊆ρb(A)∪σ1(A)=; 2)σa(M0)=σe a(M0)=D, 因此M0为f-a-isoloid且acc[isoσa(M0)]=Ø;Ø,ρSF(M0)={λ∈: |λ|≥1}, 则M0满足A-Weyl定理, 且ρSF(M0)由有限多个指标非正的连通分支构成. 因此由引理3和推论3可知, 对任意的C∈B(H)及所有的K∈K(H⊕H)且‖K‖<, 存在>0, 使得MC+K满足A-Weyl定理.

同理, 根据定理2和推论2可知, 对任意的C∈B(H),MC满足A-Weyl定理稳定性的等价条件.

推论4令A∈B(H)使得ρτ(A)⊆ρb(A)∪σ1(A),M0∈(H⊕H)为f-a-isoloid且acc[isoσa(M0)]=Ø, 则下列叙述等价:

1) 对任意的C∈B(H)及所有的K∈K(H⊕H),MC+K满足A-Weyl定理;

2) 对所有的K∈K(H⊕H), 存在C0∈B(H), 使得MC0+K满足A-Weyl定理.