雷达高度表回波模拟及扩展目标算法

， ，

(中国工程物理研究院电子工程研究所， 四川绵阳 621999)

0 引言

由于雷达高度表考虑的是大地目标的散射特性以及载体的高速运动特性，目标回波可以看作由分布于不同距离、不同方位分辨单元上的若干散射中心回波的矢量合成。这将导致雷达目标回波在时域和多普勒域的包络展宽。如果雷达高度表仍采用经典的“匹配滤波+门限判决”点目标检测方法，目标能量将不能充分利用，降低了目标的检测概率。如此特点决定了雷达高度表的目标检测算法与传统检测算法会有所不同。

现已有多种检测器已被用于雷达高度表扩展目标检测。文献[1]指出，由于目标的散射点个数、位置、幅度、相位、多普勒等信息都是未知或部分未知的，最优检测器不可实现。通常做法是根据似然函数估计未知参量，将未知参量的极大似然估计代入似然比检验，从而得到可以实现的广义似然比检测器，例如积分检测器。文献[2]对雷达高度表回波在时域及多普勒域展宽的问题进行了系统的研究，将粗糙大地简化为Brown定律和垂直入射时有镜面反射的其他粗糙表面散射模型的结合，通过对m序列脉间相位编码波形分析研究，提出并设计实现了基于“时域相关+多普勒域滤波”算法的目标检测处理系统。该算法通过设置合适的本地信号延时量，按距离单元对回波信号进行相关，在时间域实现了对天底点目标的相干积累，然后通过对多普勒域分布的能量进行非相干积累来检测大地面目标。本质上，这种算法是在目标信息完全缺失情况下由广义似然比检测推导而来，是积分检测器在脉间相位编码雷达高度表上的具体实现形式。此外，文献[3]针对雷达高度表天线宽波束带来的大地面目标回波信号频域多普勒展宽问题，提出一种基于天底点多普勒频率FFT滤波选大处理获得雷达高度表对其载体的速度测量方法。文献[4]针对安装在高速运动载体上的脉间编码雷达高度表存在的多普勒失配问题，提出一种多普勒带通滤波器和本地码延时提取速度及距离信息的检测方法。此外，文献[5-6]讨论了高速运动带来的“多普勒敏感性”问题，当回波信号的多普勒频移超过滤波器的多普勒容限带宽时，系统检测性能下降。

针对上述问题，本文从RADARSAT-1数据生成的SAR图像中提取强散射中心，结合雷达发射波形、天线方向图、雷达高度表与大地之间位置、速度的三维时空关系，仿真模拟了具有高可信度的雷达高度表目标回波信号。在此基础上，通过分析目标回波的时频特性，设计了基于散射中心时频域分布的扩展目标检测器，提高了目标的检测概率，解决了载体高速运动条件下“多普勒敏感性”问题。

1 脉间相位编码雷达高度表回波模拟

雷达高度表目标回波是由大地表面对电磁波的后向散射与反射而形成的，大地表面作为雷达高度表的目标，比一般雷达点目标要复杂得多。其中既蕴含了大地目标的散射特征信息，又蕴含了目标的运动特征信息。为了获得高可信度的雷达目标回波需要确保两方面的保真性：一是对目标电磁散射特性的保真性，二是对运动特征的保真性。

1.1 高保真目标电磁散射特性模拟

目标回波与雷达高度表发射波所照射的大地面目标的散射特性有关，此外还与发射波的入射角、极化方式和工作频率等因素有关。而且，随着频率和姿态角的不同，目标的散射场变化十分剧烈。该现象可由高频近似理论进行解释。在高频区，当一个电大尺寸目标被照射时，它的总散射场可以看作是若干个散射点或散射源发出的散射信号经矢量合成的结果[7]。随频率和角度的不同，单个散射点的散射信号的变化通常并不剧烈，但各散射点的相位会发生变化，从而导致总的散射场剧烈变化。从信号处理的角度看，雷达目标由一系列幅度和相位确定的散射中心组成，可以将目标看成一个线性系统，照射目标可等效为发射波通过目标系统，输出应为发射波与目标系统响应函数的卷积，因此可以使用目标冲击响应函数来进行建模[7]。根据这一机理，本文根据目标强散射点的分布对不同波形、不同姿态角下的雷达目标回波信号进行了模拟。其中，目标强散射点的数据来源可以是理论计算，如矩量法、SBR法、FDTD法等，也可以是实验测量数据。本文采用加拿大RADARSAT-1的成像结果作为大地目标强散射点的数据来源，该成像结果采自RADARSAT-1精细模式2，斜视角约为1.6°，入射角为37°～48°，成像带宽为30.3 MHz，标称分辨率为10 m，成像结果如图1所示。

图1 加拿大温哥华的RADARSAT-1精细模式2成像结果

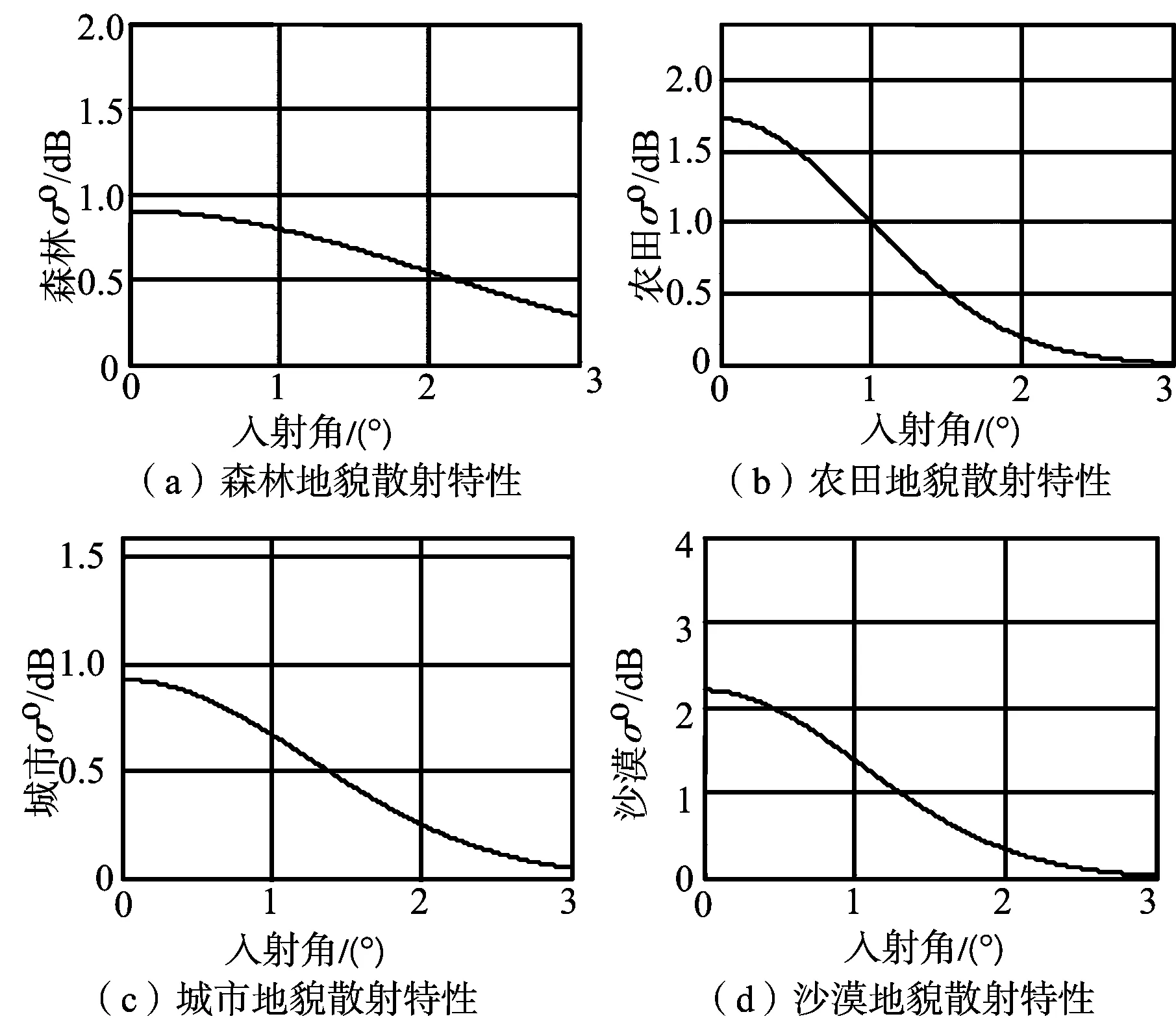
图2 4种典型地面的散射系数

1.2 高保真运动特性模拟

图3给出了雷达高度表与大地目标的几何关系示意图[1]。图中雷达处于Z轴上，距地面的高度为h，速度矢量v位于XZ平面内，θ为天线的半波束角，γ为速度矢量与Z轴的夹角。

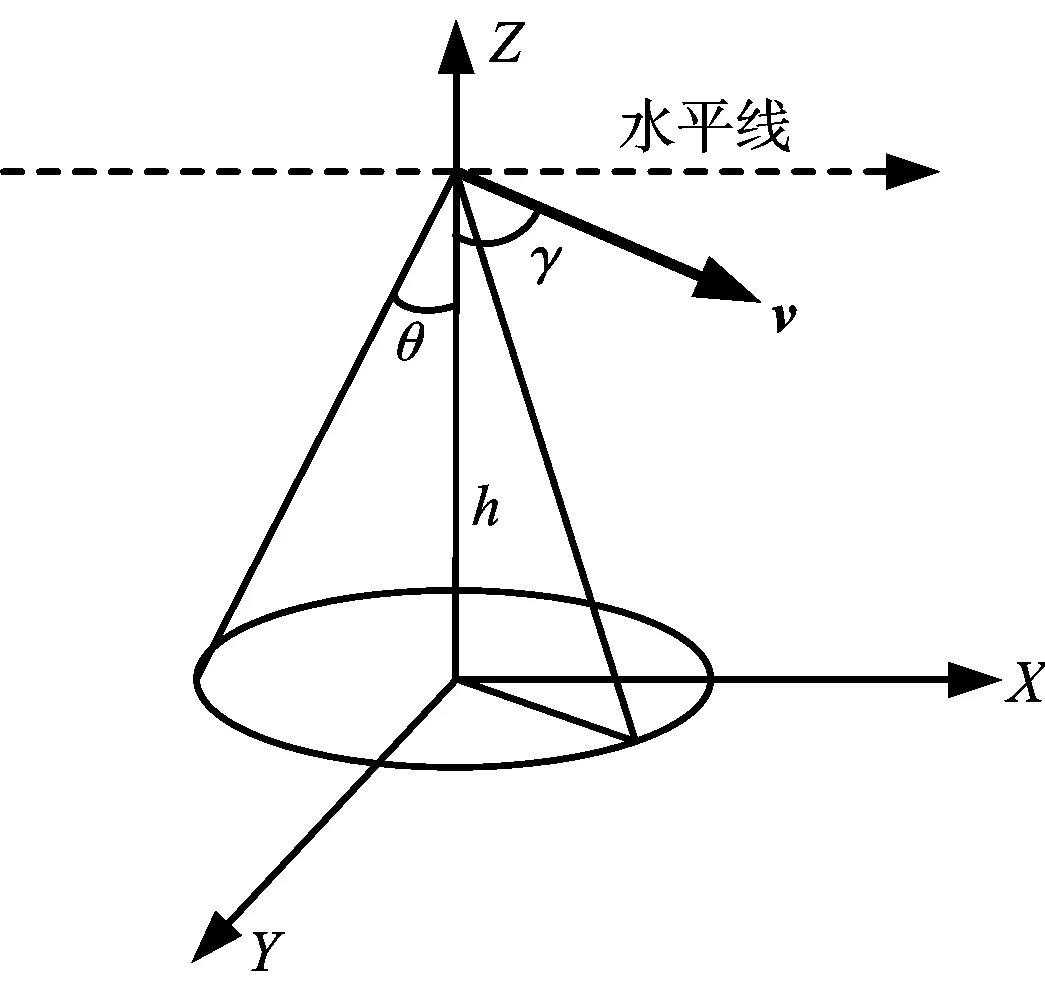
图3 雷达高度表与大地目标的几何关系

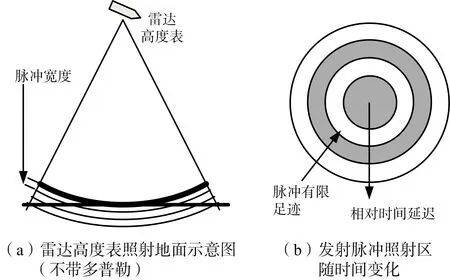
图4 雷达高度表照射区随时间变化图

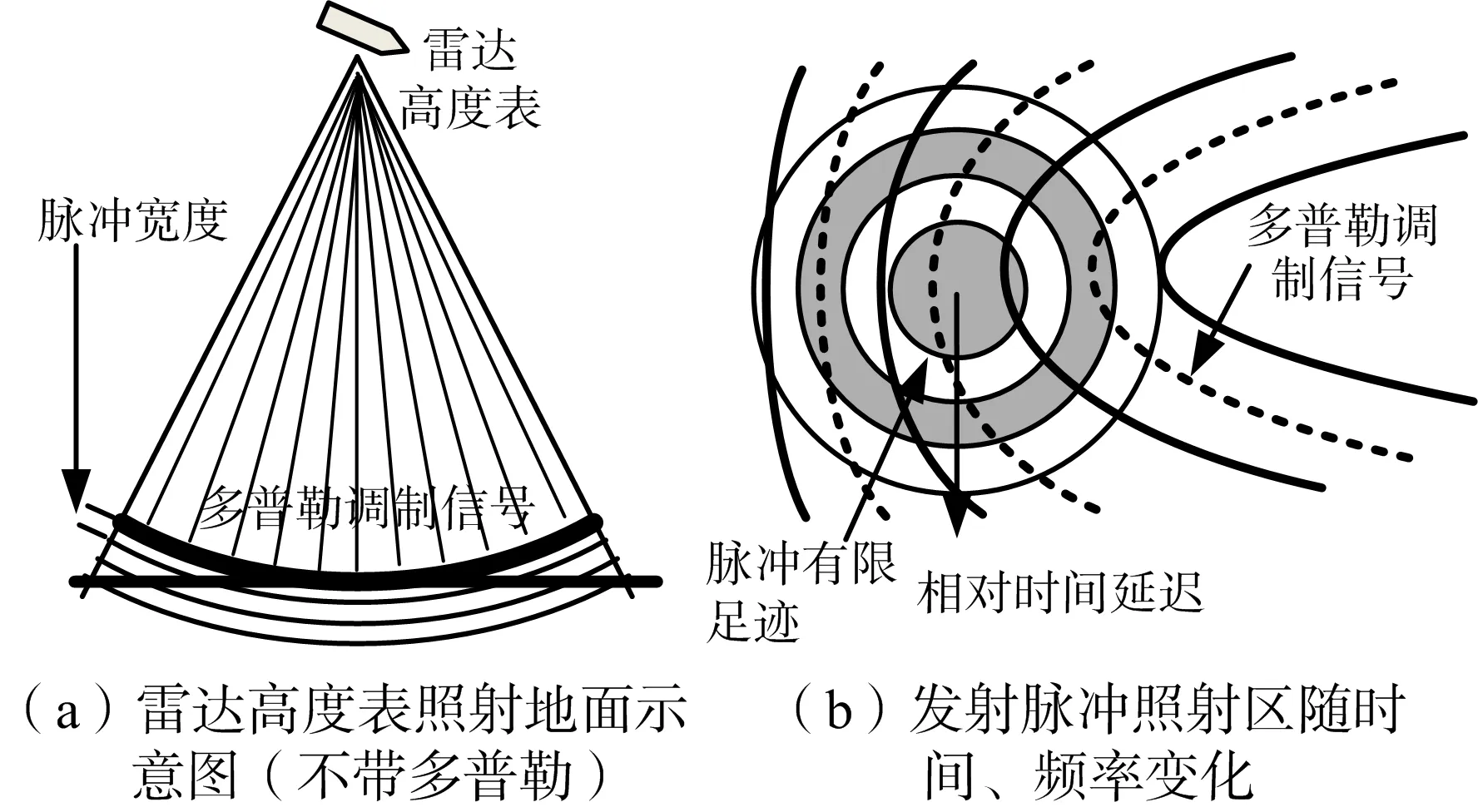
图5 雷达高度表照射区随时间、频率变化图

1.3 雷达高度表目标回波模型

根据1.1节介绍的目标强散射点模型，设散射点为理想的几何点，发射信号x(t)=s(t)ej2πft的回波信号xr(t)可写成

xr(t)=∑k∑N-1i=0GkAkrectt-nTr-τkTr·

1-rectt-nTrTr·

s(t-τk)ej2π(fc-fdk)t=

∑k∑N-1i=0GkAkrect2(t,nTr,τk)·

s(t-τk)ej2π(fc-fdk)t

(1)

式中：rect(t/Tr)为宽度等于Tp的矩形函数，Tp，Tr分别为脉冲宽度及脉冲重复周期，考虑雷达高度表采用单天线收发分时工作，[1-rect()]为收发开关，为书写简便，记rect()与[1-rect()]的乘积为rect2()；Gk为第k个散射点处的天线增益；Ak，τk，fdk，(xk，yk)分别为第k个散射点回波的幅度、高度延时、多普勒频率和位置坐标。仿真中，Ak的取值可以从合成孔径成像雷达(SAR)的图像中提取，τk，fdk的取值由雷达高度表与大地面目标的几何关系确定，其关系如式(2)所示：

2 目标回波特性

2.1 时域特性分析

由于发射波形为脉冲形式，目标上的散射点不是同时被照射，而是天底点首先被照射，然后随着时间的推移而照射偏离天底点的散射点。回波信号xr(t)在时域的理论分布如图6所示。仿真获得的回波信号xr(t)的时域分布如图7所示。图中，虚线为单次回波的仿真结果，实线为1 000次回波平均后的结果。单次回波表现为在时域的起伏，其起伏范围大都在12～16 dB之间，这是由于地物目标的回波起伏特性造成的。该结论与理论分析[9]、同行的仿真结果[10]是一致的。从图6、图7中还可以看出，回波信号包含相干反射和非相干散射两种分量，反射分量存在于回波脉冲的上升沿内，而散射分量主要存在于回波脉冲的后沿。上述结论对设计目标检测器具有指导意义。

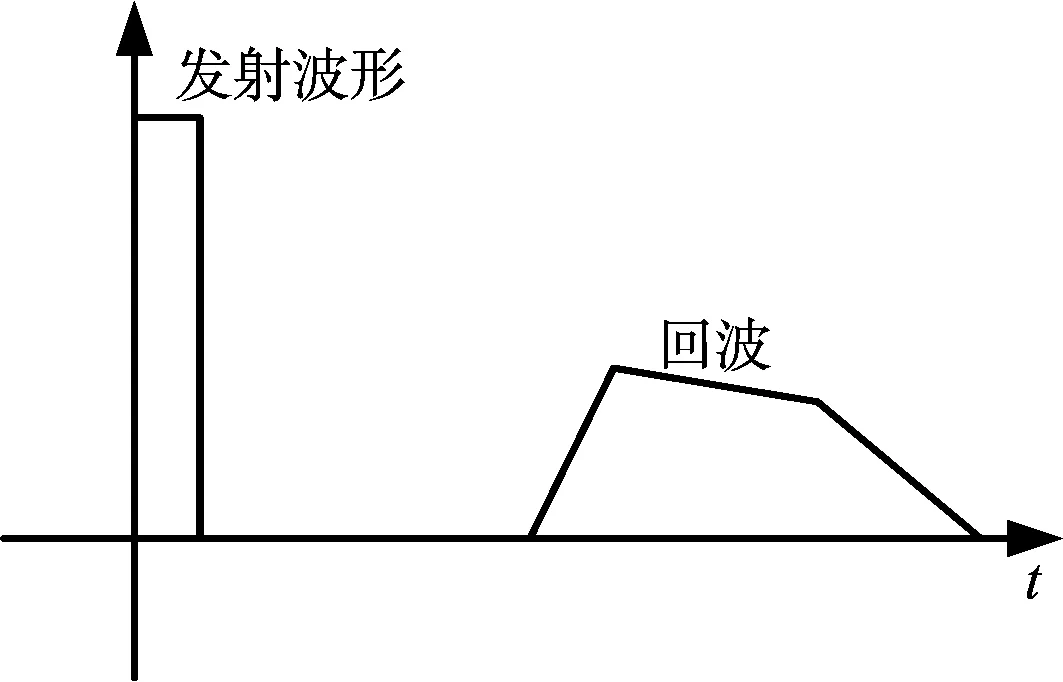
图6 雷达高度表发射脉冲与回波信号时域关系图

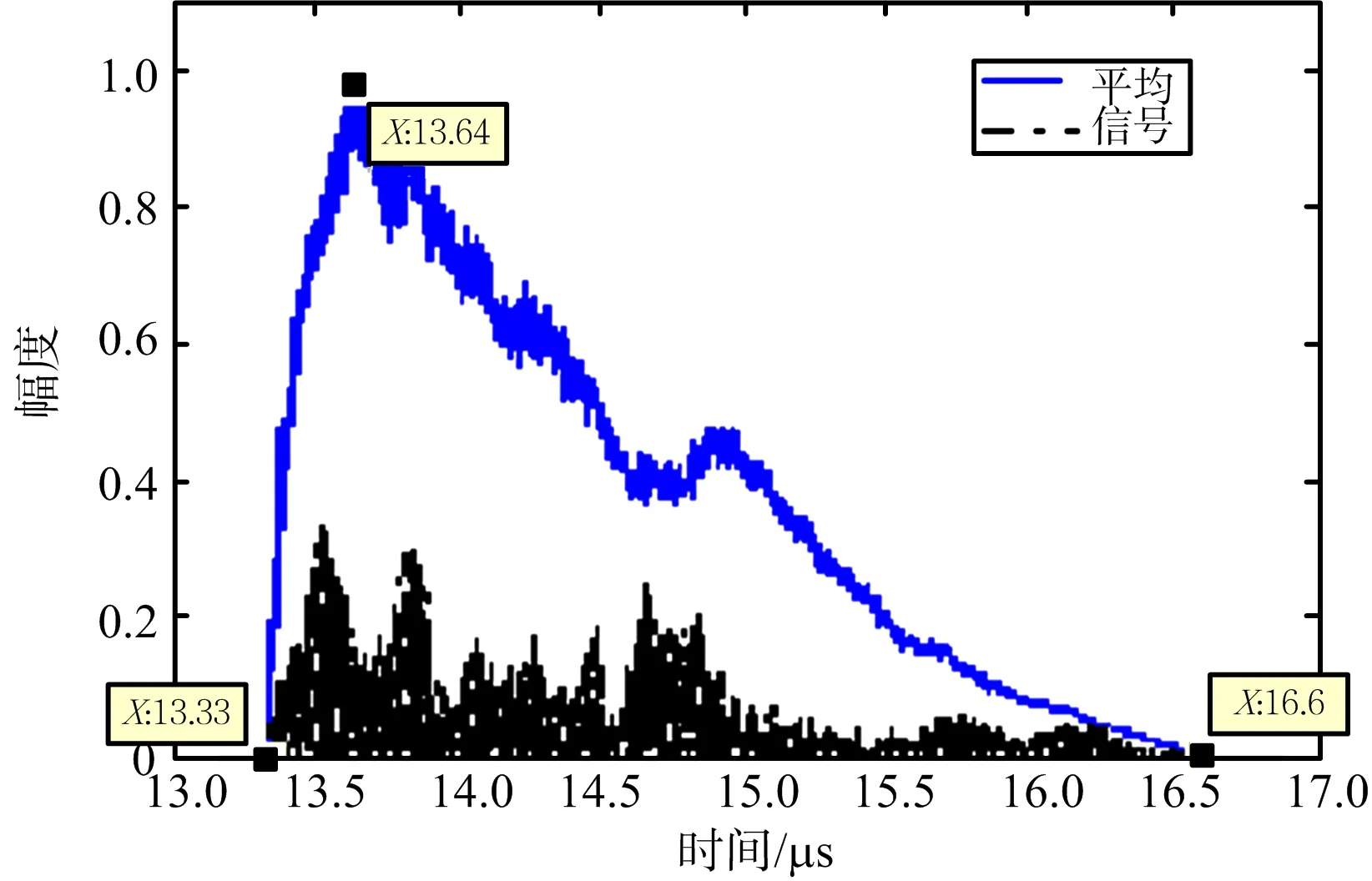
图7 回波信号在时域的分布

2.2 目标回波频域特性分析

根据1.2节的理论分析可知，回波信号xr(t)的频谱分布是由照射圆面积内各个散射点的多普勒分量矢量叠加而成。在h=3 000 m森林地貌情况下，回波信号的频谱分布如图8所示。图中，虚线为单次回波的仿真结果，实线为1 000次回波平均后的结果。在不同地貌、不同高度下，回波信号xr(t)的频域展宽各不相同，仿真结果如图9所示。从仿真结果可以得到以下有助于开展目标检测器设计的结论：

1) 由于地物目标的回波起伏特性，单次回波的多普勒包络是起伏的；

2) 回波信号除天底点附近的反射分量以外，还存在一个比反射分量要小的散射分量(森林除外)；

3) 天底点附近的多普勒反射分量的带宽分布相对整个最大照射圆的多普勒带宽较小，而能量分布相对较多；

4) 随着高度的降低，回波信号的频谱宽度展宽。

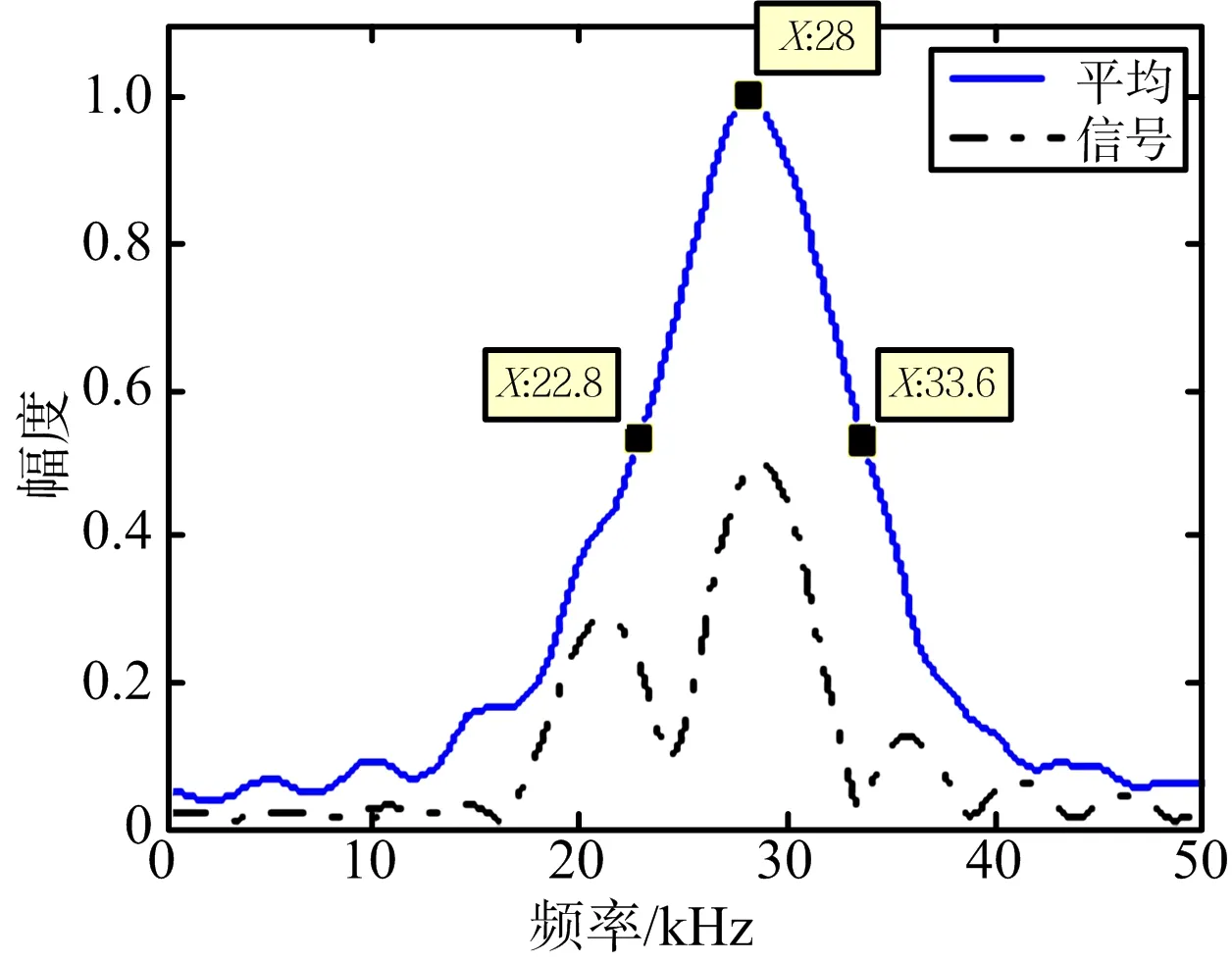
图8 回波信号在频域的分布

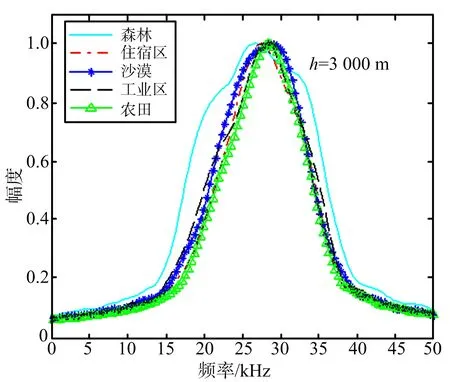
(a) 同一高度不同地貌回波信号频谱分布

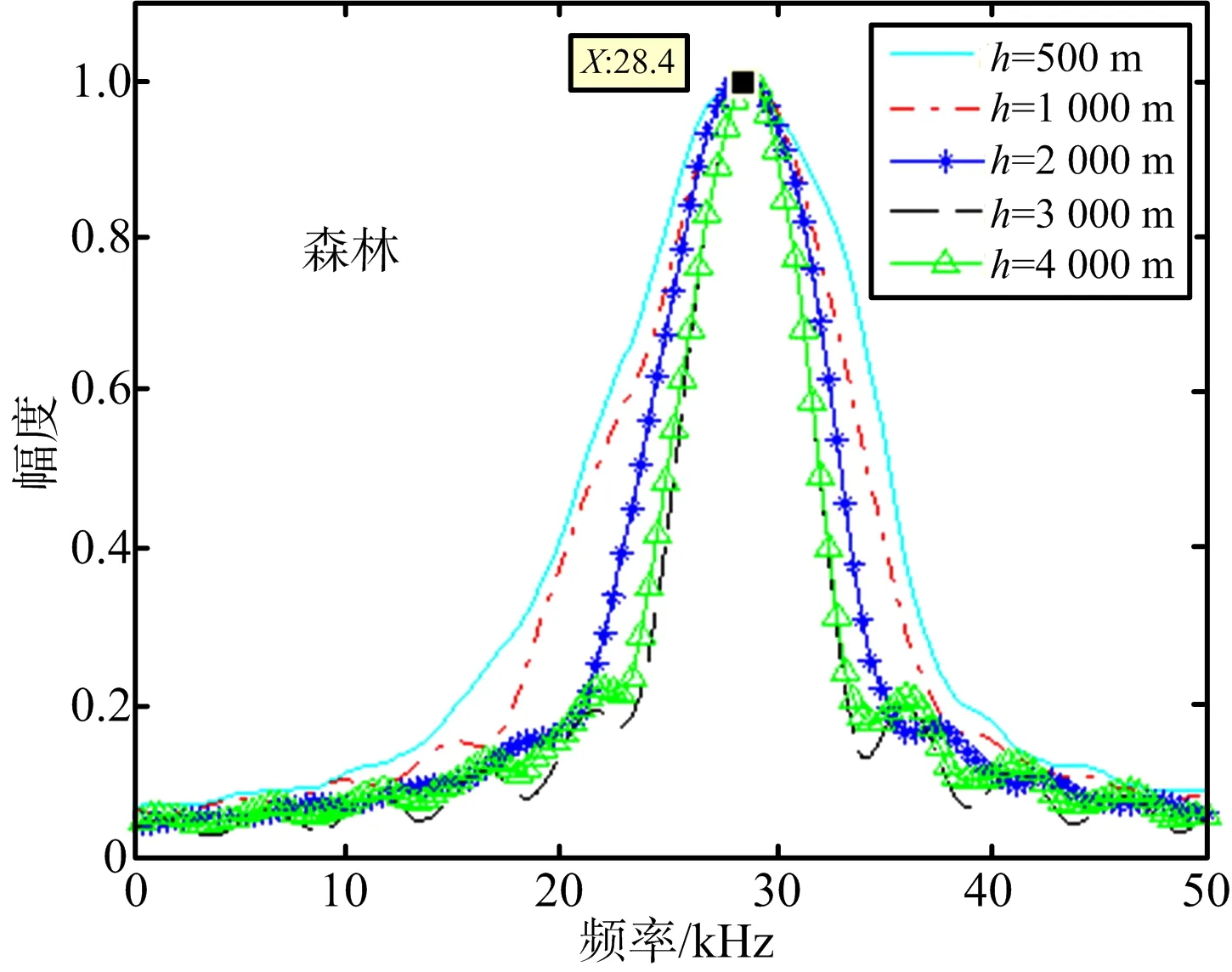
(b) 森林地貌不同高度回波信号频谱分布图9 不同地貌不同高度的回波信号频谱分布

3 基于扩展目标的目标检测算法

由第2节的分析可知，雷达高度表目标回波在时域和多普勒域的包络是展宽的，且功率起伏幅度在12～16 dB之间，这给传统目标检测带来了困难。不过当进行扩展目标检测时，目标回波的时频域特性就变为必要的信息。问题的关键是怎样把目标回波的时频域分布概率密度等先验信息与扩展目标检测算法相结合，设计出新的雷达高度表目标检测算法。文献[11]给出了等效散射中心假设下目标回波的近似表达式：

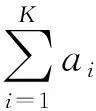
δ(t-Ti-T0)+w(t)

(3)

式中，θ为目标姿态角，K为散射中心个数，ai(θ)为第i个散射中心的幅度，φi(θ)为第i个散射中心的相位，T0为目标质心到雷达高度表的距离产生的时间延迟，Ti为第i个散射中心到目标质心在雷达视线上的距离产生的时间延迟，w(t)为接收机的复平稳高斯白噪声。目标检测的任务是根据输入信号判断目标是否存在，通常可以表示为一个二元假设检验问题:

H0:x[n]=w[n]

在理想条件下，假设目标的所有信息都是已知的，根据Neyman-Pearson准则，最优检测器为似然比检验。一种方法是，首先发射一个高分辨率波形对环境进行搜索，并用去卷积算法处理回波信号以提取环境的响应，然后用这一响应来形成发射波形和匹配接收机以检测目标[12]，当然这种最佳匹配接收很难实现。在实际中，现有多种检测器已被用于高分辨雷达扩展目标检测，如积分检测器、序贯检测器(OS-RSTD)[13]、基于散射中心密度的双门限检测器(BSD-M/N)[14]、SDD-GLRT检测器[15]、基于散射点个数估计的双门限检测器(BS-GLRT)[11]。其中，BS-GLRT检测器考虑散射点个数的概率分布，通过改进积分检测器中目标散射点个数的估计方法，提高了检测器性能。本文考虑目标回波时域和多普勒域的功率概率密度，并结合BS-GLRT检测，提出了一种适用于雷达高度表的目标检测方法。该方法通过改进积分检测器中目标散射点个数的估计方法，达到尽可能接近排序积累检测其性能的目标[1]。该检测系统的信号处理流程如图10所示。首先，对接收信号作多普勒补偿、匹配滤波等相干处理。然后，选定第一门限λ1，将匹配滤波后的输出信号取模求平方。最后，将超过λ1的距离单元的值求和累加，并与第二门限作λ2比较得出判决。其中，第一门限λ1可根据AIC准则来选取，如式(5)所示。第二门限的值可根据虚警率通过仿真来选取。

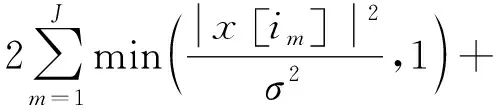
2Jlnπσ2

(5)

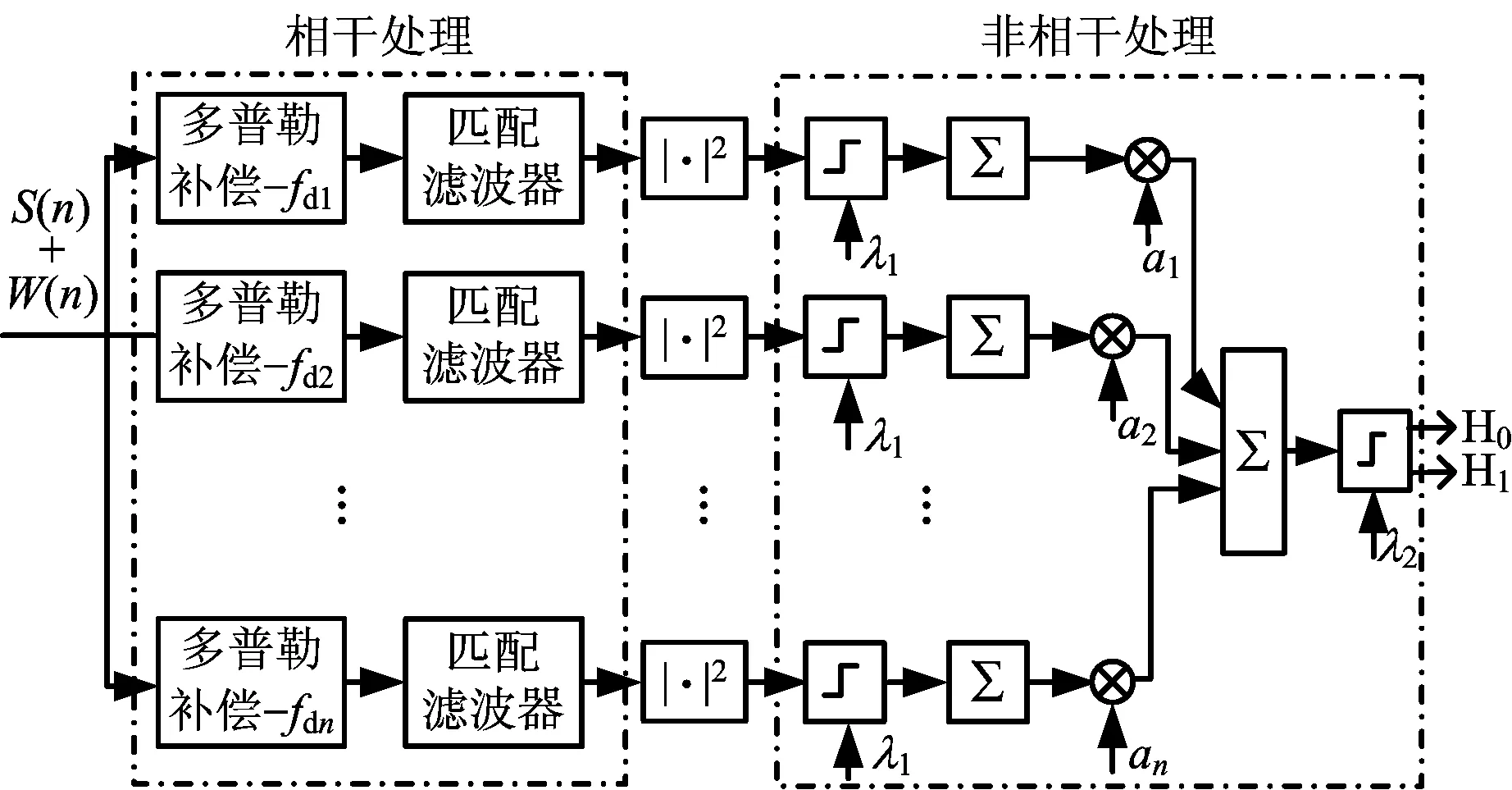
图10 检测器信号处理流程图

4 仿真

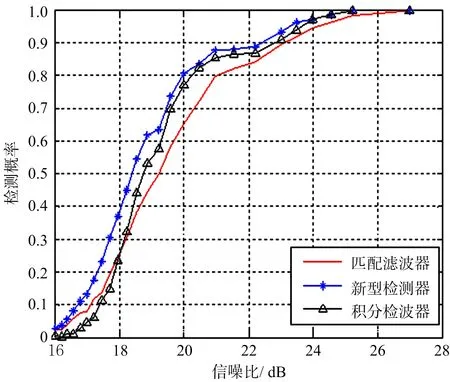
图11 性能检测曲线

5 结束语

本文将目标回波看作是若干个散射点散射信号的矢量合成，并考虑载体高速运动对各个散射点散射信号的多普勒调制，提高了雷达高度表目标回波仿真的可信度；在此基础上，进行了不同地形地貌、不同高度的大地回波信号模拟。理论分析和仿真结果均表明，雷达高度表回波信号具有明显的时域和多普勒域二维展宽和功率起伏特性。这些特性对传统目标检测器的设计带来了困难，同时也给扩展目标检测器带来了不可多得的先验信息。基于上述分析，设计了一种适用于雷达高度表的改进BS-GLRT检测算法。仿真表明，该检测算法的性能优于现有的检测算法。