多普勒盲区下基于GM-CBMeMBer的多目标跟踪算法
2018-11-06,,,,
, , , ,
(空军预警学院, 湖北武汉 430019)
0 引言
在机载多普勒雷达多目标跟踪(Multi-Target Tracking, MTT)过程中,多普勒盲区(Doppler Blind Zone, DBZ)的存在是不可回避的现实问题[1-3]。DBZ问题由传感器物理限制产生,当目标的径向速度小于最小可检测速度(Minimum Detectable Velocity, MDV)时,目标无法被传感器检测,这将导致目标漏检和航迹中断,严重影响跟踪性能[4]。
文献[5]提出了基于高斯混合(Gaussian Mixture, GM)的跟踪算法,它通过引入伪造量测来代表漏检,通过构造合适的状态依赖的检测概率,使其在DBZ里的检测概率值较低。然而,由此得到的高斯混合近似可能有负的权重,造成数值不稳定。文献[6]提出了“两伪造点”分配方法,其中,一个伪造量测代表对应检测概率小于1造成的漏检,另外一个额外的伪造量测代表由于DBZ引起的漏检。文献[7]基于二维分配方法,通过对来自同一目标的不同时间段航迹进行关联,提出了航迹段关联(Track Segment Association, TSA)方法。
然而,上述算法的实现涉及复杂的数据关联问题,实用性有待提高。作为一种可替代传统基于数据关联算法的方法,基于随机有限集(Random Finite Set, RFS)的多目标跟踪算法在解决DBZ问题中有着显著优势。其中,文献[8-9]分别将概率假设密度(Probability Hypothesis Density, PHD)和势化概率假设密度(Cardinalized PHD, CPHD)应用于DBZ条件下的地面动目标指示(Ground Moving Target Indicator, GMTI)跟踪。不同于PHD传递一阶矩、CPHD传递二阶矩和势分布,文献[10]提出的势平衡多目标多伯努利(Cardinality Balanced Multi-Target Multi-Bernoulli,CBMeMBer)滤波器通过传递多伯努利RFS来递推估计后验多目标概率密度。
CBMeMBer滤波器提供的“假设航迹”机制更有利于解决DBZ条件下的多目标跟踪问题,不过在CMeMBer框架下的相关研究还鲜有报道,所以本文在CBMeMBer滤波器中引入MDV和多普勒信息,并给出了其高斯混合执行,记为GM-CBMeMBer-D-MDV。仿真结果表明,所提滤波器能有效地改善DBZ下多目标跟踪性能。
1 CBMeMBer滤波器
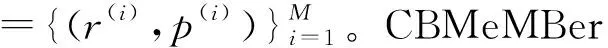
1.1 预测步
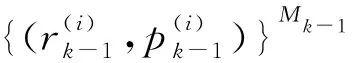
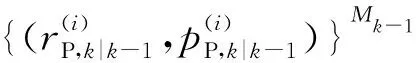
(1)
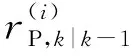
(2)
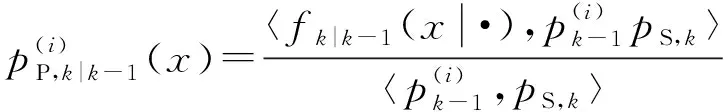
(3)
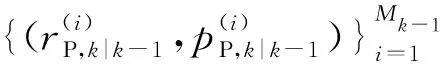
1.2 更新步
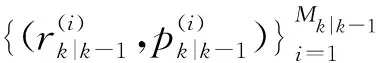
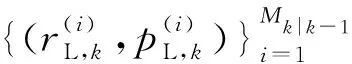
(4)
Mk|k-1=Mk-1+MΓ,k
(5)
(6)
(7)
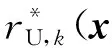
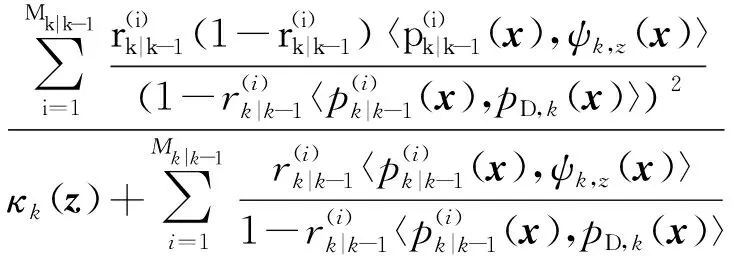
(8)
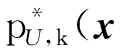
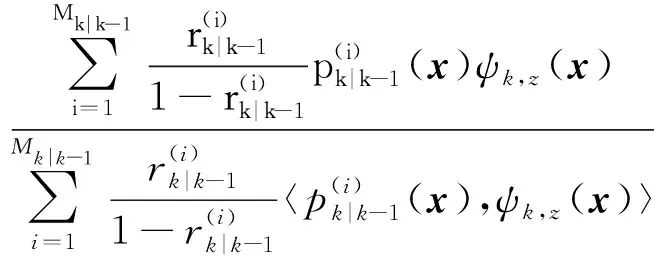
(9)
ψk,z(x)=gkz|xpD,k(x)
(10)
式中:pD,k(x)为目标检测概率;Zk为k时刻量测集合;κkz为杂波强度;gkz|x为目标量测似然函数。
2 带最小可检测速度和多普勒信息的GM-CBMeMBer滤波器
2.1 并入最小可检测速度的检测概率模型
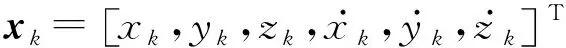
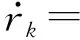
(11)
(12)
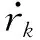
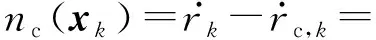
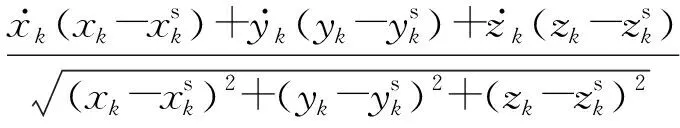
(13)
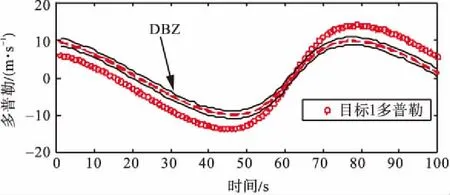
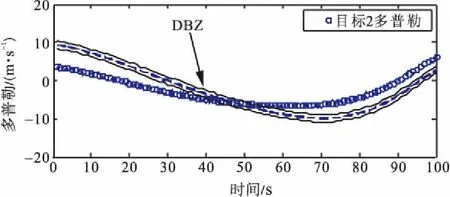
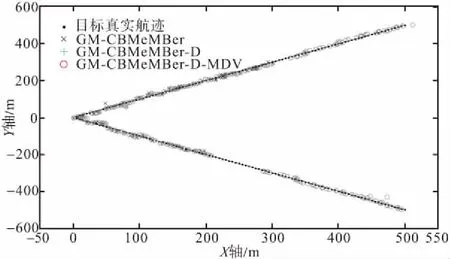
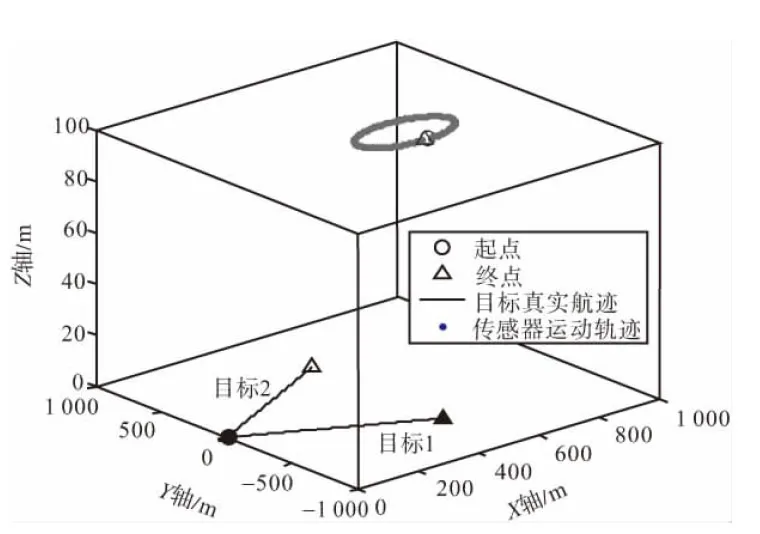
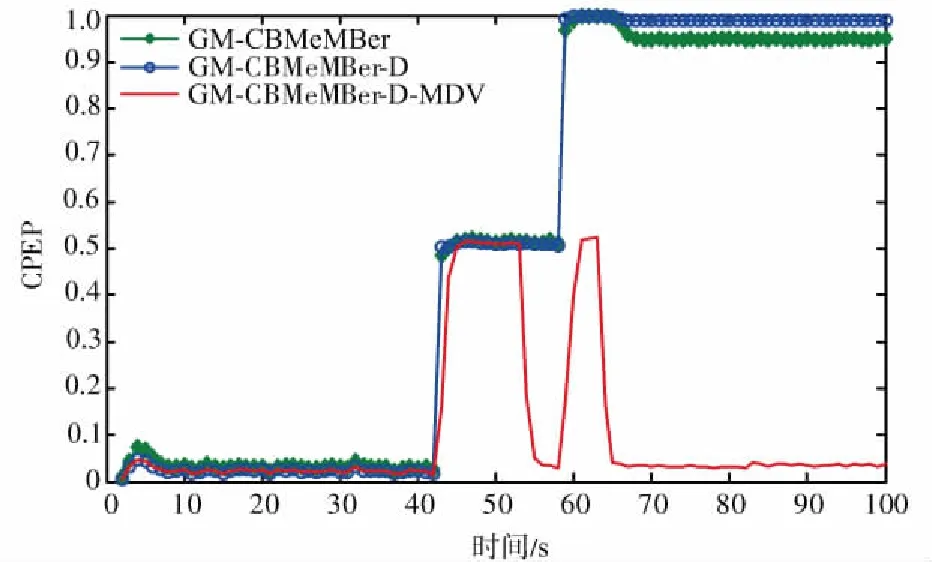
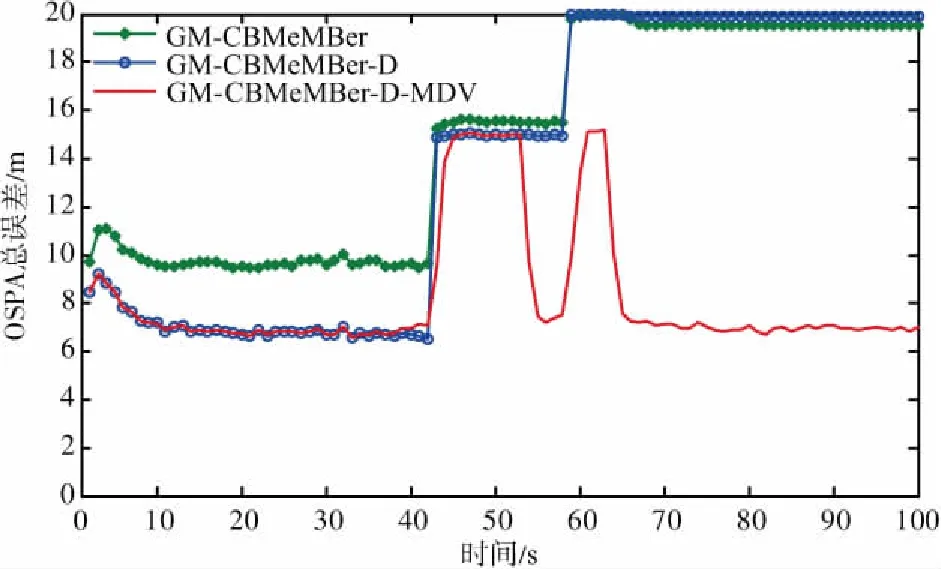
目标检测概率pD,kxk是关于目标状态的函数,并且受DBZ强烈影响。具体而言,当nc pD,kxk≈pD1-exp-nc(xk)/MDV2·ln2 (14) 式中,pD为目标远离DBZ的检测概率值。 (15) 式中,伪量测函数yf和伪量测矩阵Hf分别为 (16) n1,n2,n3,n4,n5,n6T (17) 将式(15)代入式(14),进一步化简得到检测概率的高斯形式: (18) (19) (20) 在推导GM-CBMeMBer-D-MDV的更新公式的过程中,利用了下述两个引理[12]: 引理1:给定适当维度的H,R,m和P,且R和P是正定的,则有 Nz;Hx,RNx;m,P= Nz;Hm,SN(x;m+G(z-Hm),P-GSGT) (21) 式中,S=HPHT+R,G=PHTS-1。 引理2:给定适当维度的F,Q,m和P,且Q和P是正定的,则有 N(z;Fm,Q+FPFT) (22) 假设目标xk-1在k时刻存活,则xk-1转移到xk的概率转移密度函数为 fk|k-1(xk|xk-1)=N(xk;Fk-1xk-1,Qk-1) (23) 式中,Fk-1为状态转移矩阵,Qk-1为过程噪声协方差。 对于多普勒体制雷达,式(10)中的量测似然函数gk(z|x)可以建模为 (24) 式中,z为k时刻的常规量测,包括位置量测yc和多普勒量测yd,且两者不相关,Hc,k为线性位置观测矩阵,Rc,k为位置观测噪声协方差,σd为多普勒观测噪声标准差,hd,k(x)为式(11)的非线性多普勒观测函数。 (25) 将式(18)的检测概率模型和式(24)的似然函数代入式(4)中,连续使用两个引理得到GM-CBMeMBer-D-MDV的更新公式: (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) 式中,伪量测增益和伪量测新息协方差分别为 (36) (37) (38) (39) (40) (41) (42) 式中,位置量测增益和位置量测新息协方差分别为 (43) (44) 多普勒量测增益和多普勒量测新息协方差分别为 (45) (46) (47) (48) (49) (50) (51) 式中,伪量测增益和伪量测新息协方差分别为 (52) (53) κk(z)=κc,k(yc)κd,k(yd) (54) (55) (56) (57) 式中,κc,k(yc)为位置分量杂波强度,κd,k(yd)为多普勒杂波强度。 此外,伯努利RFS和高斯分量随着时间迭代不断增加,如果不对其进行有效的管理,将严重影响滤波器运行效率,所以在完成更新步骤后,还需要进行“剪枝合并”操作[10]。 下面有3点值得注意: 1) 当MDV=0且cf=0时,GM-CBMeMBer-D-MDV变为带多普勒量测的GM-CBMeMBer,简记为GM-CBMeMBer-D。 为了验证所提滤波器的有效性,在相同参数下比较GM-CBMeMBer,GM-CBMeMBer-D和GM-CBMeMBer-D-MDV三种滤波器的跟踪性能。 基于上述参数设置,图1给出了传感器和目标的真实航迹,图2给出了MDV=1 m/s条件下各时刻目标多普勒速度与DBZ的关系。由图2可知,因为目标多普勒速度值小于MDV,所以目标2和目标1分别在43~52 s和59~63 s处于DBZ。图3给出了MDV=1 m/s条件下3种滤波器单次跟踪结果比较,通过比较可知,当目标离开DBZ,仅GM-CBMeMBer-D-MDV能够再次跟踪目标。 (a) 目标1 (b) 目标2图2 各时刻目标多普勒与DBZ的关系 图3 单次跟踪结果比较 图1 传感器和目标的真实航迹 利用圆位置误差概率(Circular Position Error Probability, CPEP)[13]和最优子模式分配(Optimal Sub-Pattern Assignment, OSPA)[14]比较3种滤波器的跟踪性能。其中,CPEP可以反映滤波器对目标的“漏跟”概率,定义为 (58) 令位置误差半径r=20 m,OSPA的阶参数p=2,截止参数c=20 m。在MDV=1 m/s条件下进行1 000次蒙特卡洛仿真,图4和图5给出了3种滤波器的CPEP和OSPA总误差统计结果。由图4可知,在43~52 s阶段,目标2处于DBZ内,而目标1处于DBZ之外,所以3种滤波器均无法跟踪目标2,但都能跟踪目标1。因此,3种滤波器在这段时间的CPEP均保持在0.5左右,而图5中3种滤波器的OSPA总误差都处于较高的值,约为15 m。当目标2在第53 s离开DBZ后,GM-CBMeMBer-D-MDV能够再次跟踪目标2,对应的CPEP和OPSA总误差回到目标2进入DBZ前的水平。但是GM-CBMeMBer和GM-CBMeMBer-D无法有效保存处于DBZ内的目标状态,当目标2处于DBZ内,传感器无法获得目标量测,所以更新步骤结束后,多伯努利RFS的存在概率逐渐减小直至低于门限P,最后在“剪枝合并”过程中被删除。目标2离开DBZ后,GM-CBMeMBer和GM-CBMeMBer-D无法再次跟踪目标2,所以它们的CPEP和OPSA总误差分别继续保持在0.5和15 m左右。类似地,在59~63 s阶段,目标1处于DBZ内,此时GM-CBMeMBer和GM-CBMeMBer-D均无法跟踪两个目标。因此,它们的CPEP和OSPA总误差进一步升高到1和20 m左右。当目标1在第64 s离开DBZ后,GM-CBMeMBer和GM-CBMeMBer-D的CPEP和OSPA总误差继续维持在1和20 m左右,说明它们均无法再次跟踪目标1。而GM-CBMeMBer-D-MDV的CPEP和OPSA总误差减小到目标1进入DBZ前的水平,说明其能够再次跟踪目标1。 图4 3种滤波器的CPEP比较 图5 3种滤波器的OSPA总误差比较 针对DBZ条件下机载多普勒雷达对目标航迹跟踪不连续的问题,提出了带最小可检测速度和多普勒信息的GM-CBMeMBer滤波器(GM-CBMeMBer-D-MDV)。该滤波器首先将带MDV的检测概率模型代入CBMeMBer中,然后给出其详细的预测和更新步骤。蒙特卡洛仿真实验结果表明,相对于未并入MDV信息的GM-CBMeMBer和GM-CBMeMBer-D,GM-CBMeMBer-D-MDV能够有效处理DBZ条件下的多目标跟踪问题,提高DBZ下机载多普勒雷达多目标跟踪性能。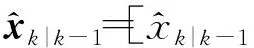
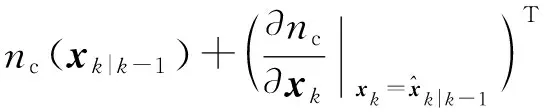
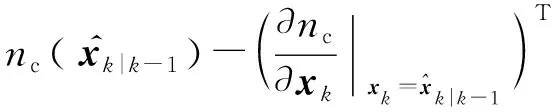
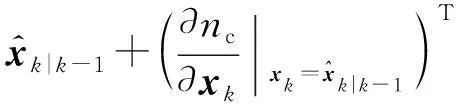
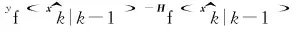
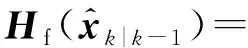
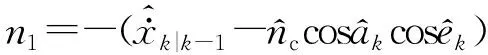
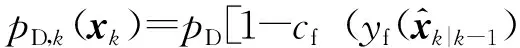
2.2 GM-CBMeMBer-D-MDV更新公式
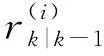
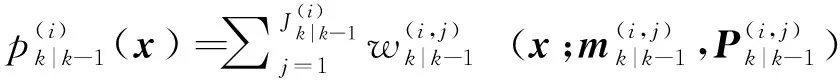
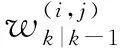
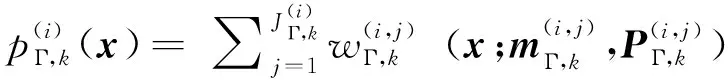
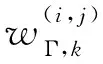
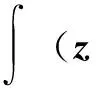
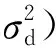
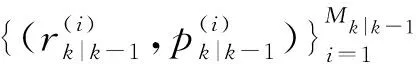
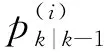
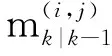
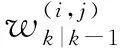
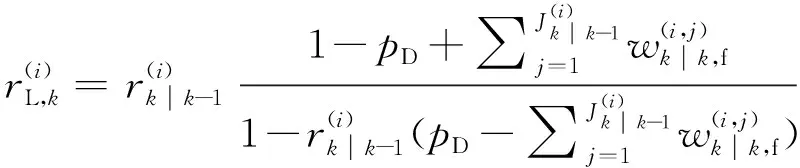
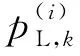
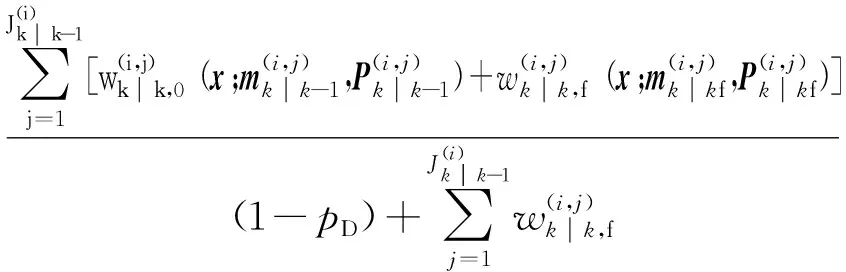
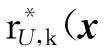
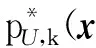
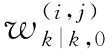
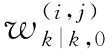
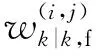
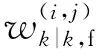
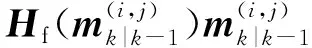
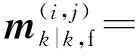
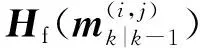
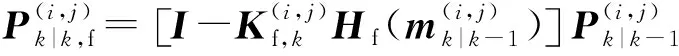
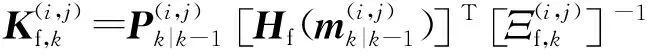
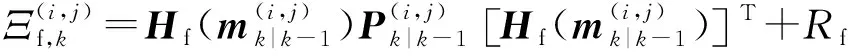
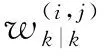
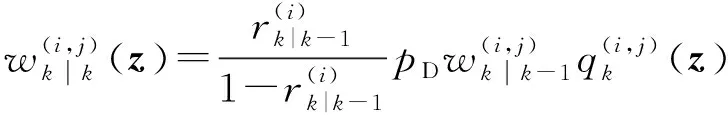
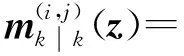
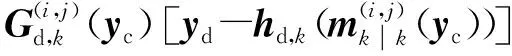
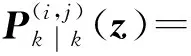
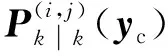
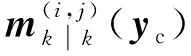
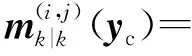
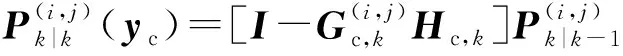
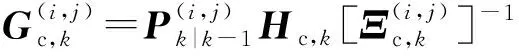
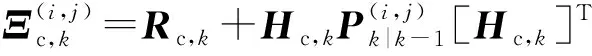
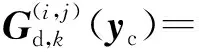
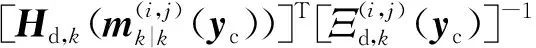
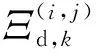
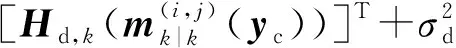
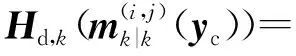
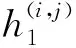
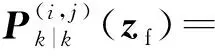
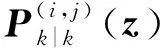
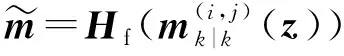
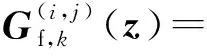
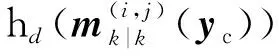
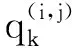
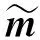
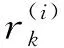
3 仿真与分析
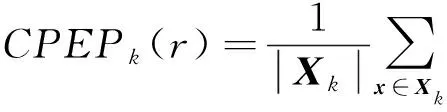
4 结束语
