基于改进Quinn算法的LFMCW雷达高精度测距

， ， ，

(重庆邮电大学重庆市移动通信技术重点实验室， 重庆 400065)

0 引言

LFMCW雷达具有距离分辨率高、发射功率低、没有距离盲区、结构简单且成本低廉等优点，使其广泛地运用在地面和海上监控雷达，特别是在现代军事中的地位越来越重要。线性调频连续波雷达信号是把发射端产生的本振信号和遇到目标反射回来的回波信号进行混频，得到差拍信号，然后从差拍信号中提取目标信息。在LFMCW雷达体制中，从时域中提取目标信息非常困难，需要对差拍信号作快速傅里叶(Fast Fourier Transform，FFT)变换。在同步采样期间，离散频谱信号各次谐波频率的位置是采样频率分辨率的整数倍，不会引起由FFT变换后产生的栅栏效应，但同步采样在实际中很难实现，需要对栅栏效应问题进行处理。目前降低栅栏效应的办法可以通过提高采样间隔，即提高频率分辨率的办法来解决。

传统时域降低栅栏效应的方法是在有效采样数据序列后面补零，这种方法在一定程度上确实降低了栅栏效应，但不能提高分辨精度，而且只能在采样点数缺少的情况下使用。传统频域降低栅栏效应的算法有Macleod算法[1]、Quinn算法[2-3]、改进的Rife (Improved Rife，IRife)算法[4]、IRife算法与Quinn算法的融合算法(R-Quinn)[4]等，其中IRife算法在频率偏差处于频谱附近时测距精度很高，Macleod算法在IRife基础上引入频率偏差因子提高测距精度，相比较IRife算法测距精度更高。Quinn算法在频率偏差处于量化频谱附近时测距精度不高，但在量化频谱中间时，测距精度却很高。根据这一特性，一些科研工作人员通过结合IRife和Quinn算法，提出了R-Quinn来提高LFMCW测距精度，测距误差在3 m左右。但为了能实现更高的测距精度，本文提出了一种改进的Quinn算法，使频率偏差无论处在两量化频谱之间的任何地方，都能获取较高的测距精度，测距误差在1 m左右。

1 LFMCW原理

在连续波雷达系统中，发射端通过直接数字式频率合成器(Direct Digital Synthesizer，DDS)不停地进行上下扫频，产生线性扫频信号(本振信号)并通过天线发射出去，发射出去的信号接触到目标后再反射回来称为回波信号，最后把本振信号和回波信号进行混频得到差拍信号[5]。以三角波调制雷达为例，设三角波的周期为T，发射信号扫描的频偏为B，电磁波的传播速度为光速c，差频频率为fi，则测量距离为

在没有噪声的情况下，差拍信号可以看成一个频率为fi的正弦信号。由于信号在经过天线发射出去再反射回来后，不可避免地会产生噪声，因此可以把差拍信号看作一个正弦信号和噪声信号的叠加，它的表达式为

s(t)=Aej2πfit+θ0+w(t)

(2)

s(n)=Aej2πfin/fs+θ0+w(n)

(3)

s(n)=A+Awej2πfin/fs+θ0+θw

(4)

式中，Aw表示噪声的幅度，θ0表示噪声的相位，频率估计公式如下所示：

式中，k0为s(n)的离散傅里叶谱峰对应的频点，δ为实际频率峰值与理论峰值对应的偏差，即频率偏差。

2 Quinn算法原理分析

为了方便对信号进行处理，只考虑有效信号s(n)，对s(n)作FFT变换可得S(k)，并对S(k)取模运算，最后从S(k)的模中找到最大谱线位置记作k0，k0-1和k0+1分别是最大频率谱左右两边的次大数据。

Quinn算法是利用信号FFT主瓣内幅度次大谱线与最大谱线的FFT系数复数模值之比进行插值，该算法需要找到最大频谱位置以及两个左右相邻的次大频谱位置，通过计算最大值频谱与左右两个次大频谱的模比值确定δ。

a=ReSk0-1×ReSk0

(8)

b=ReSk0-1×ReSk0

(9)

式中，S(k)表示S(k)的模，通过式(6)和式(7)可以得到

(10)

(11)

频率偏差为

δ=δ1，a>0,b>0

δ2， 其他

(12)

通过式(5)可得频率的估计值，并结合文献[3]可知，Quinn算法在信号频率接近量化频率时，距离估计误差最大，在量化频率中间时，却可获得非常高的精确度。

3 改进后的Quinn算法原理及计算量分析3.1 改进后的Quinn算法原理分析

通过第2节对Quinn算法的优缺点介绍可知，当频率偏差处于两量化频谱中间时，Quinn算法的频率估计方法可以获得较高测距精度。根据这一特性，改进的Quinn算法通过引入频率偏差因子，先把频率偏差搬移到两量化频谱中间，再用Quinn算法进行频率估计。具体做法如下所示：

1) 对s(n)进行FFT变换得到S(k),并对S(k)进行求模处理得到S(k)。

2) 找到S(k)中最大谱线位值S(k)的频率点记作k0，k0-1和k0+1分别对应的是次大频谱值Sk0-1和Sk0+1。

3) 根据步骤2)中找出的3个值，求出信号实际频率与最大频率谱所对应的频率偏差因子：

由式(13)可知，把N看成一个很大的数值时，γ近似为

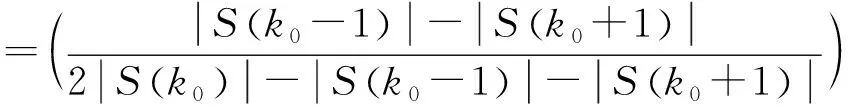
(14)

根据所求频率偏差因子，可得到频率偏差δ1为

4) 把信号频带移动δ1+θ个量化单位，考虑到δ1的取值范围是-0.5,0.5，同时为了确保把真实信号频谱搬移到两个相邻最大谱的中间，不妨把θ的值定为0.5。通过式(16)、式(17)和式(18)可以求得频谱搬移后的频点对应的频率谱:

Xk0+δ1+θ=

Xk0-1+δ1+θ=

Xk0+1+δ1+θ=

5) 根据式(12)并结合步骤4)可以计算出频率偏差δ2。

6) 最后把以上步骤计算的参数代入式(5)可得到新的信号频率估计为

3.2 计算量分析

Quinn算法需要作一次N点FFT变换，即N/2log2N次复数乘法和N/2log2N复数加法运算，Macleod算法和Quinn算法的计算量一样。改进后的Quinn算法计算出信号频偏估计fi，需要作一次FFT和3次DFT变换。DFT只需要对一个点作FFT变换，算法复杂度要低于一次FFT变换，因此，它需要的计算量是N/2log2N+3N复数乘法和Nlog2N+3N-1复数加法，R-Quinn算法需要作一次FFT和两次DFT变换。算法计算量比较如表1所示。虽然说改进后的Quinn算法的计算量略大于Quinn算法、Macleod算法和R-Quinn算法，但是在连续波雷达体制中为了提高检测精度和性能，这点资源就显得不足为虑了。

表1 各算法计算量比较

4 仿真分析

为了测试改进后的Quinn算法的性能，本文分别对Macleod算法、Quinn算法、R-Quinn以及改进后的Quinn算法进行Matlab仿真分析。由式(2)可知，LFMCW雷达信号可以用正弦信号和一个噪声信号表示，设采样频率为2.5 kHz，采样长度为512，相位和幅度已知，为了方便观察，把相位区间定义为-π,π。

4.1 不同频率相对偏差的估计性能

仿真参数设置如下：为了验证改进的Quinn算法在不同环境下的适应能力，设定在上述正弦信号参数不变的情况下，分别加入信噪比(SNR)为0,5,10 dB的噪声，相对频偏δ在-0.5～0.5之间取21个离散点，每个频点进行1 000次Monte Carlo仿真。同时为了仿真的严谨性，引进了CRLB进行比较[6-7]，当复正弦信号的初始相位未知、频率不是二分之一或者零的采样频率的条件下，CRLB界限可表示为

归一化均方差(Normalized Mean Square Error，NMSE)的表达式如下[8]:

3种算法的NMSE和SNR进行对比，如图1、图2和图3所示。

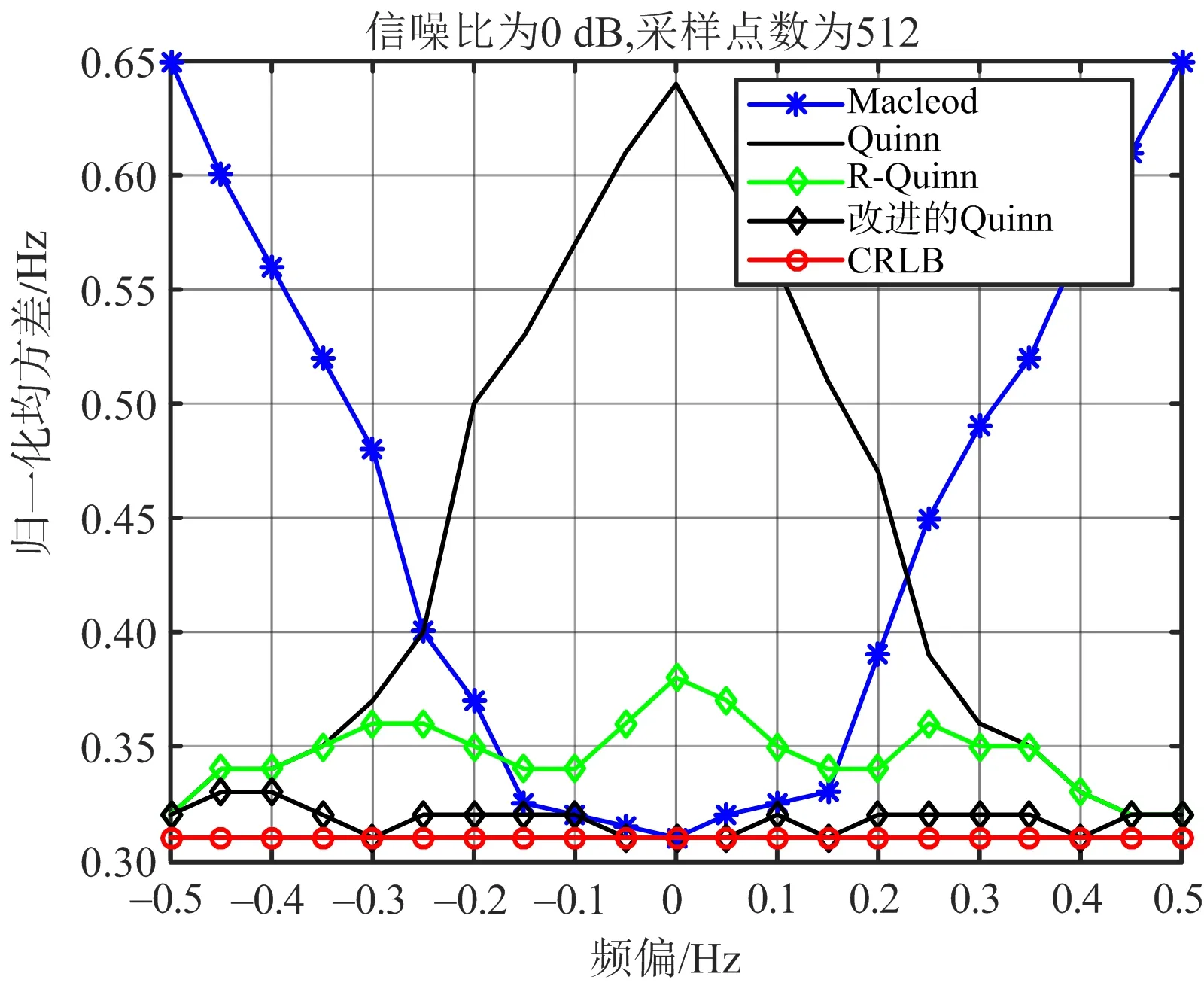
图1 SNR=0 dB不同算法的归一化均方差与CRLB的对比图

图2 SNR=5 dB不同算法的归一化均方差与CRLB的对比图

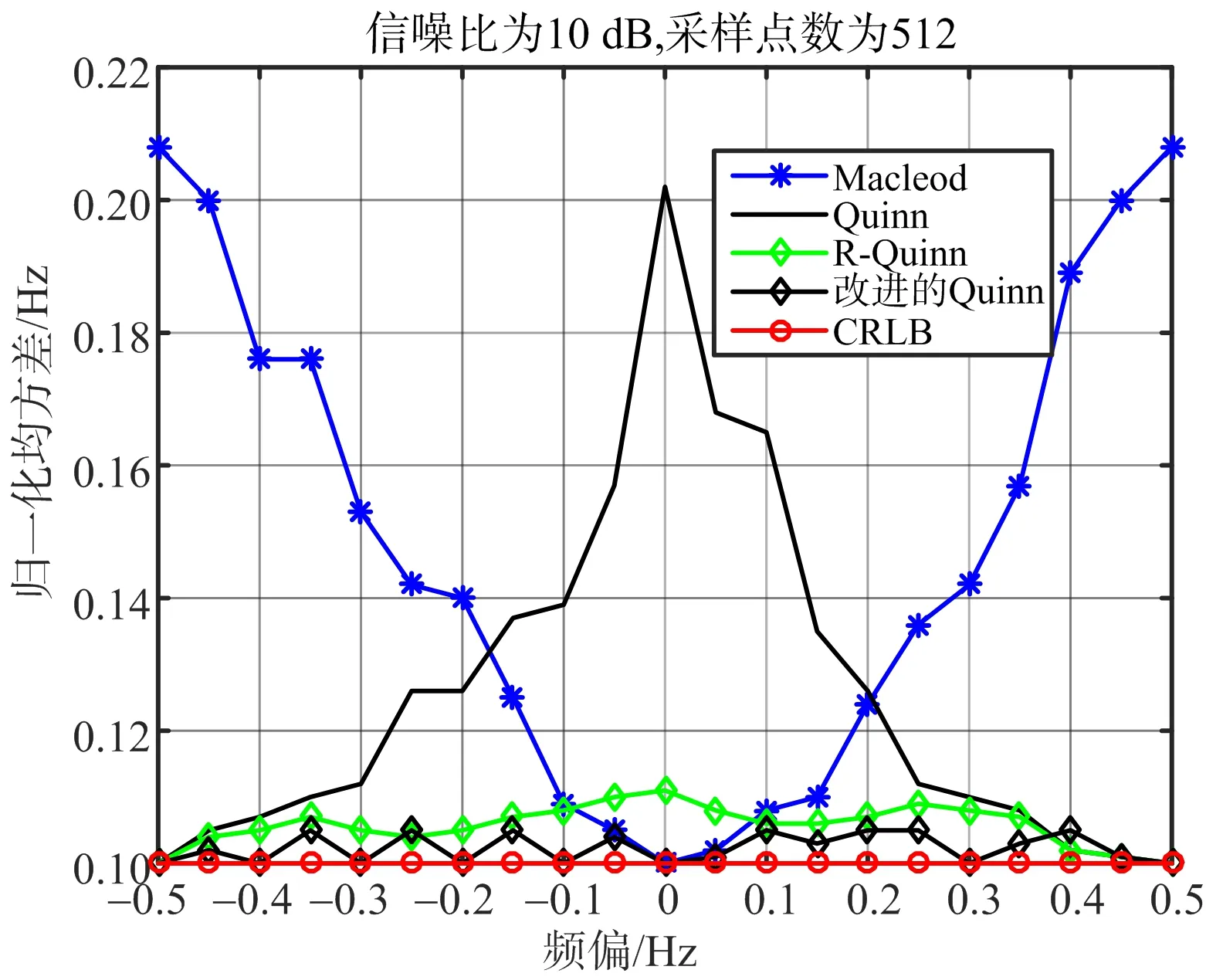
图3 SNR=10 dB不同算法的归一化均方差与CRLB的对比图

通过以上对比可知，在不同信噪比情况下，相对频偏接近零时，Quinn算法归一化均方差最大，Macleod算法的频率估计归一化均方差接近CRLB；当相对频偏接近±0.5时，Quinn算法的测距精度最高，频率估计归一化均方差接近CRLB，Macleod算法的估计精度最差。R-Quinn算法在整个相对频率估计精度仿真中，性能比较稳定，但在低信噪比环境下性能有点降低。改进后的Quinn算法在整个相对频率估计范围内，性能都更加平稳，在高/低信噪比环境中频率估计均方根误差都更加接近CRLB。

4.2 不同噪声的估计性能

仅通过把信噪比设置为0，5，10 dB来验证改进后的Quinn算法的抗噪声性能,显然还不够充分。为了进一步研究新算法的抗噪声性能，仿真参数设置如下：设定在上述正弦信号参数不变的情况下，分别在信号中加入相对频偏δ为0，0.25，0.5，信噪比在-2～12 dB之间取15个离散点，并在每个信噪比离散点下进行1 000次Monte Carlo仿真，得到的仿真结果如图4、图5和图6所示。

图4 δ=0不同算法的归一化均方差与CRLB的对比图

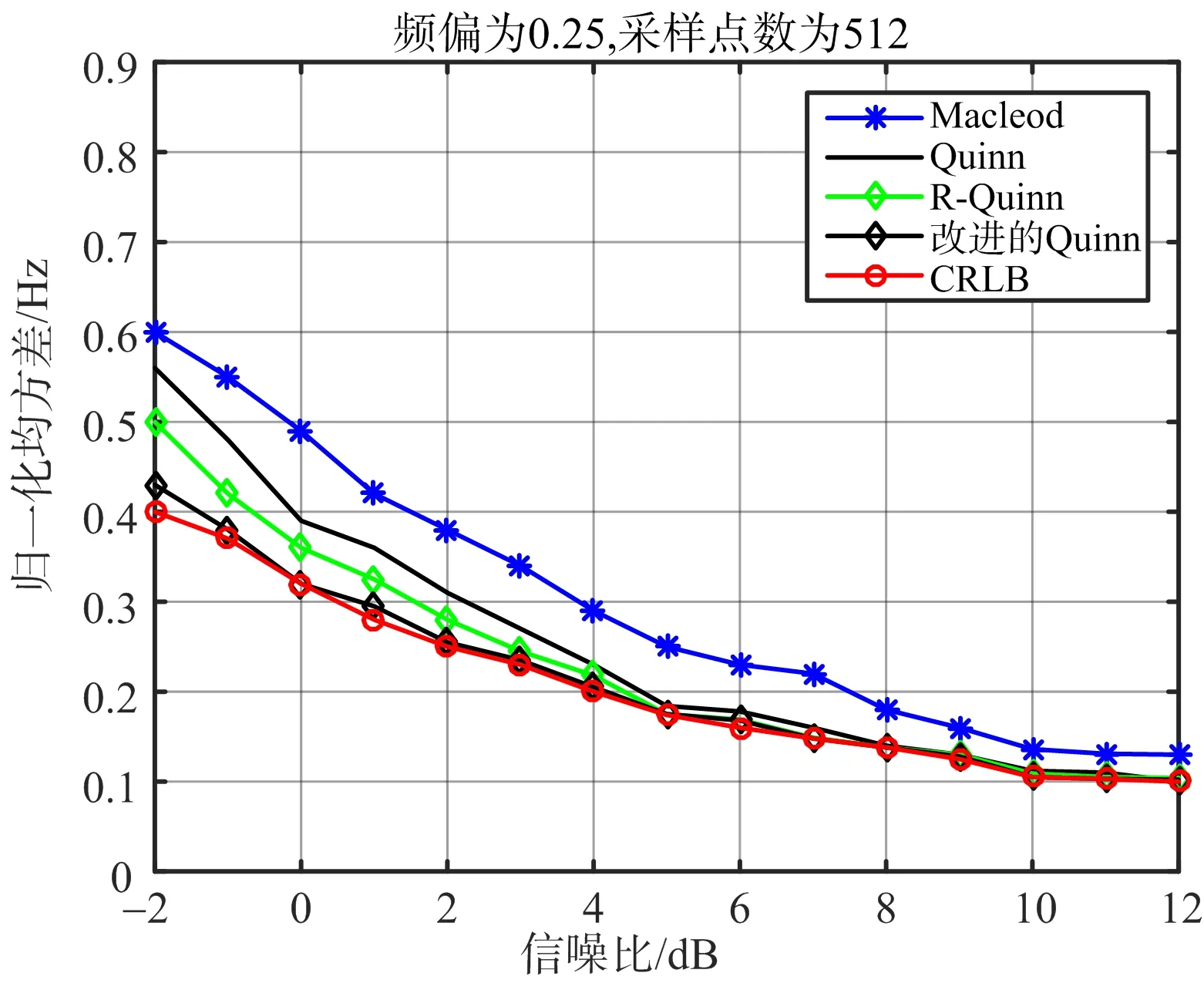
图5 δ=0.25 不同算法的归一化均方差与CRLB的对比图

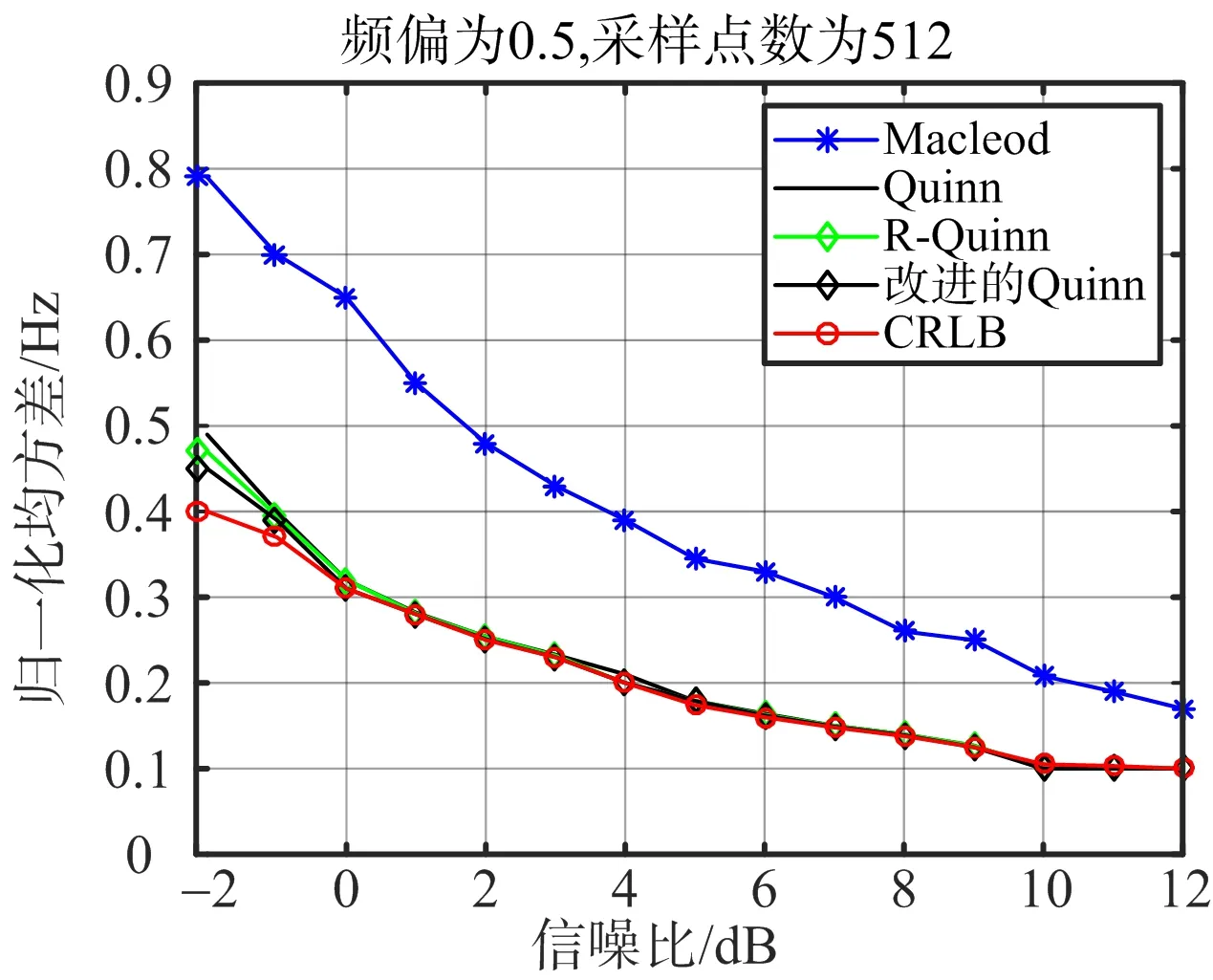
图6 δ=0.5 不同算法的归一化均方差与CRLB的对比图

通过对比发现，在不同信噪比情况下，当相对频偏δ=0时，改进后的Quinn算法和Macleod算法的归一化均方差更接近CRLB，R-Quinn算法性能次之，Quinn算法的性能最差；当相对频偏δ=0.25时，在不同信噪比情况下，改进后的Quinn算法的归一化均方差最接近CRLB，R-Quinn算法的归一化均方差比Quinn算法略高，Macleod算法最差；当相对频偏δ=0.5时，在不同的信噪比下，改进后的Quinn算法、R-Quinn算法与Quinn算法的频率估计归一化均方差都最接近CRLB，Macleod算法最差。从以上仿真分析可知，改进后的Quinn算法的频率估计归一化均方差最接近CRLB，即使是在低信噪比的情况下，测距精度依然很高。

4.3 测距精度分析

为了进一步验证改进后的Quinn算法对测距精度的影响，把信噪比设置为0 dB，引入10个静目标，分别为100，200，300，500，600，800，1 000， 1 200，1 400和1 600 m。对目标进行仿真如图7、图8和图9所示。

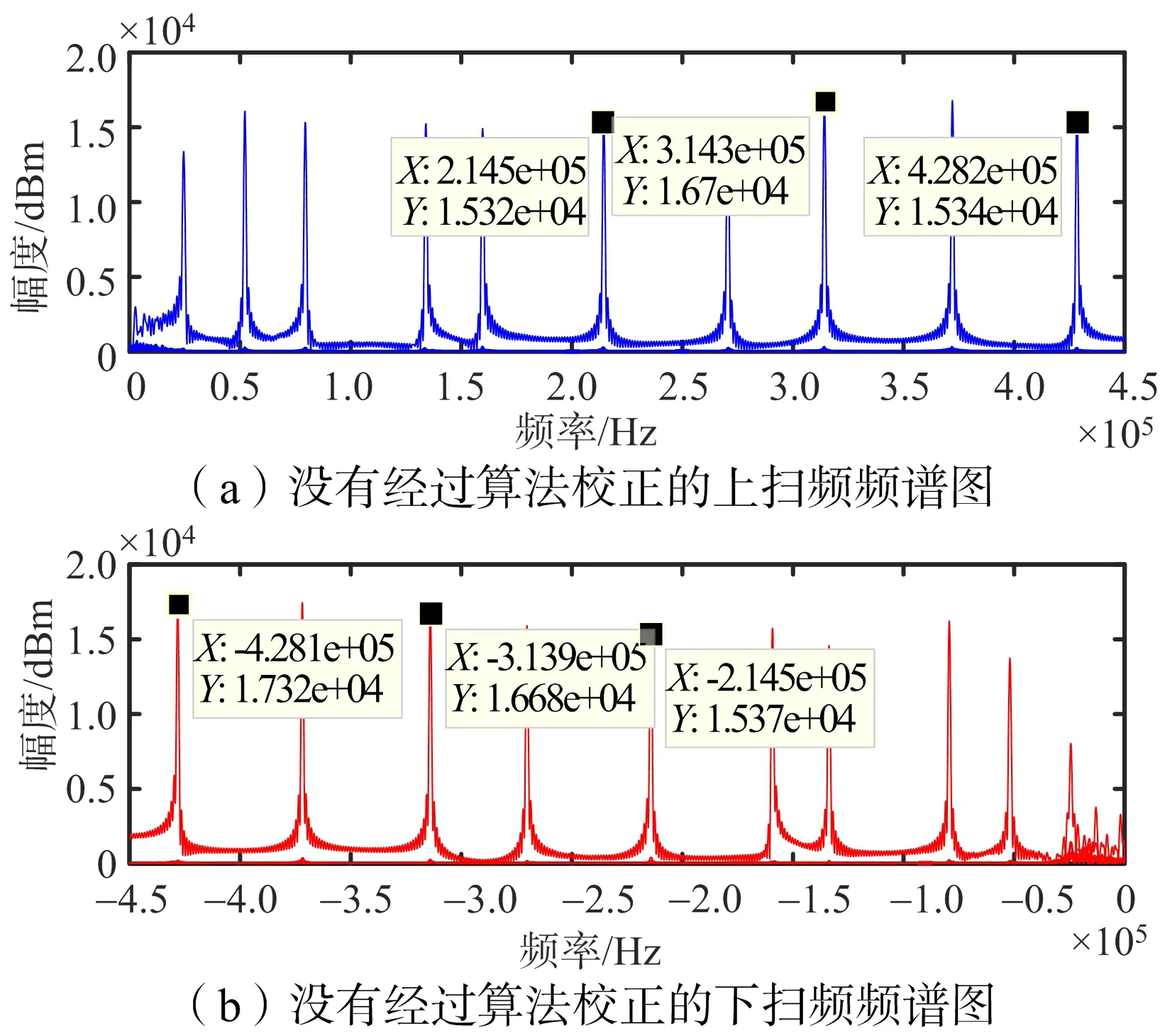
图7 没有经过频率校正的上下扫频信号目标频点

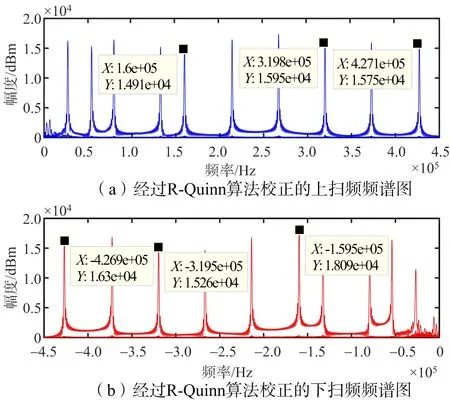
图8 经过R-Quinn算法校正的上下扫频信号目标频点

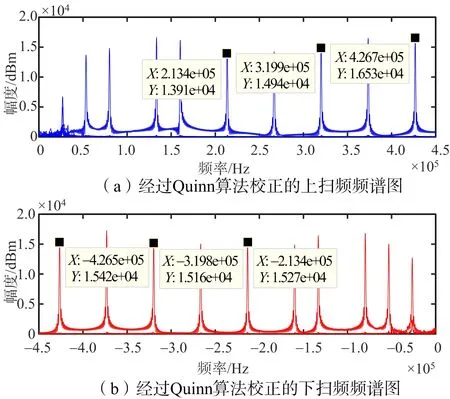
图9 经过改进的Quinn算法校正的上下扫频信号目标频点

通过表2可知，未经过频率校正的目标频点测距误差在1.959 3～14.102 2 m之间；经过R-Quinn算法校正的目标频点测距误差在0.759 0～ 3.037 8 m之间；经过改进的Quinn算法校正的目标频点的测距误差在 0.128 9～0.437 5 m之间。经过数据对比可以发现，改进的Quinn算法测距精度是最好的。

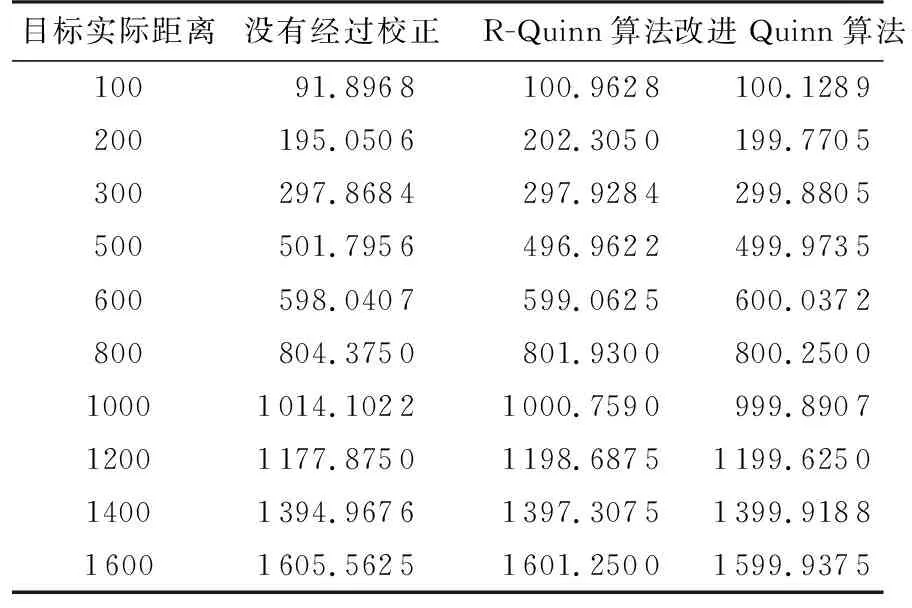
表2 各算法测距值 m

5 结束语

针对Quinn算法在相对频偏接近量化频谱时测距精度很低的问题，提出了改进后的Quinn算法，该算法具有很高的测距精度以及抗噪声性能。仿真结果表明，该算法测距精度高，估计均方根误差接近CRLB，整体性能优于Macleod算法、Quinn算法和R-Quinn算法，具有很高的工程应用价值。