FGM环扇形板的面内自由振动分析
2018-11-05滕兆春朱亚文
滕兆春, 朱亚文, 蒲 育
(1.兰州理工大学 理学院,兰州730050;2.兰州工业学院 土木工程学院,兰州730050)
1 引 言
板是土木、海洋、机械、核工业和航空航天等工程中重要的承载构件之一,环扇形板也经常用于某些特殊结构中,因此对于环扇形板的力学行为,特别是环扇形板动态特性的分析研究具有十分重要的意义。环扇形板自由振动的核心问题是求解其固有频率和相应振型。虽然有大量关于环扇形板横向自由振动的研究文献[1-3],但是关于其面内自由振动分析研究的文献相对较少[4]。已有研究结果表明,面内振动不仅对于高频振动和能量传输起着重要作用,而且还与环境的辐射噪声具有直接关系[5]。
近年来随着新型材料的兴起,功能梯度材料FGM(Functionally Graded Material)作为一种新型复合材料,具有减缓热应力、残余应力和应力集中等优异力学性能[6],故FGM 环扇形板在核工业、船舶和航空航天等高科技领域具有很大的应用价值。在实际应用中,FGM环扇形板的材料属性一般均沿板厚度方向梯度变化,但也会遇到材料属性沿径向变化的情况,以满足结构不同部位对材料性能使用的不同要求。目前,关于FGM环扇形板面内自由振动问题的研究在国内外还鲜有文献报道。因此,本文考虑材料物性参数沿环扇形板的径向按照幂级数形式梯度变化,用二维微分求积法DQM(Differential Quadrature Method)来研究FGM环扇形板的面内自由振动问题。
2 控制微分方程的推导
如图1所示,考虑单位厚度FGM环扇形板,其材料物性参数仅沿径向变化,弹性模量为E,密度为ρ,泊松比为μ,外半径为Ro,内半径为Ri,环扇形板的扇形角为φ,径向位移分量为u,环向位移分量为v,环扇形板内部(r=Ri处)为完全金属材料,外部(r=Ro处)为完全陶瓷材料。FGM环扇形板的物性参数P(弹性模量E,密度ρ和泊松比μ)与径向坐标r和梯度指标p满足混合率公式(1)[7],
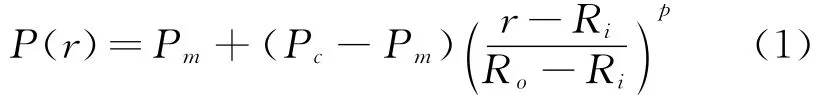
式中Pm和Pc分别为金属和陶瓷的物性参数。忽略
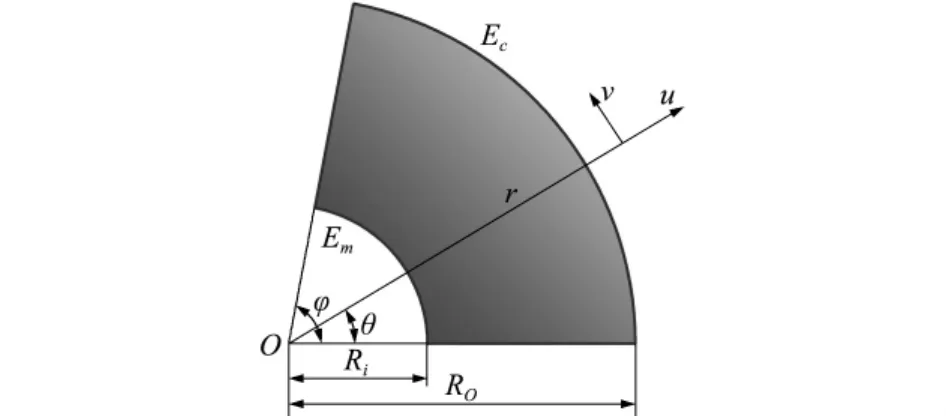
FGM环扇形板的体积力,由平面线弹性理论,在极坐标系下考虑其几何方程:
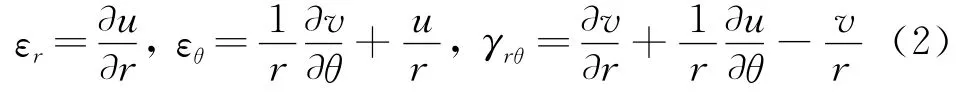
物理方程:

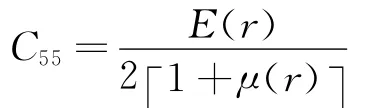
运动方程:
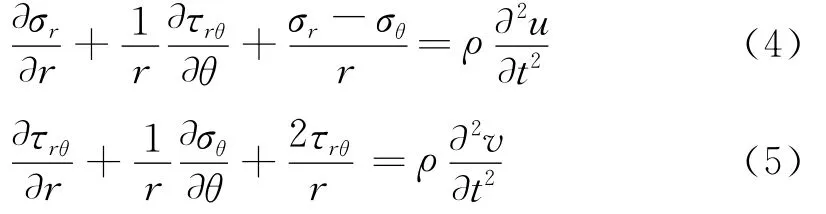
将式(2,3)代入式(4,5)得

式中 ()(1)=d()/dr,t为时间。对于随时间变化的谐波振动,FGM环扇形板面内自由振动的位移可假设为[8]
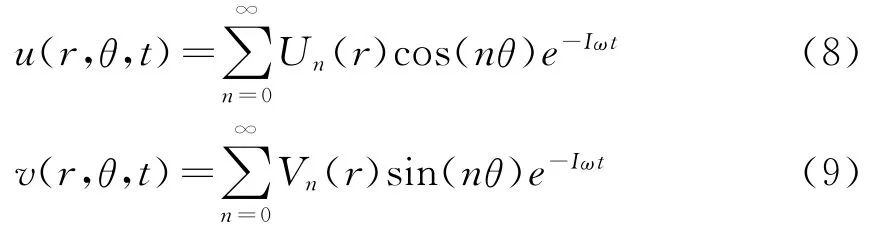
式中n为环向波数,I=槡-1为虚数单位,ω为固有频率。将式(8,9)假设的响应代入式(6,7)中,通过三角函数系的正交性可得FGM环扇形板面内自由振动的控制微分方程:
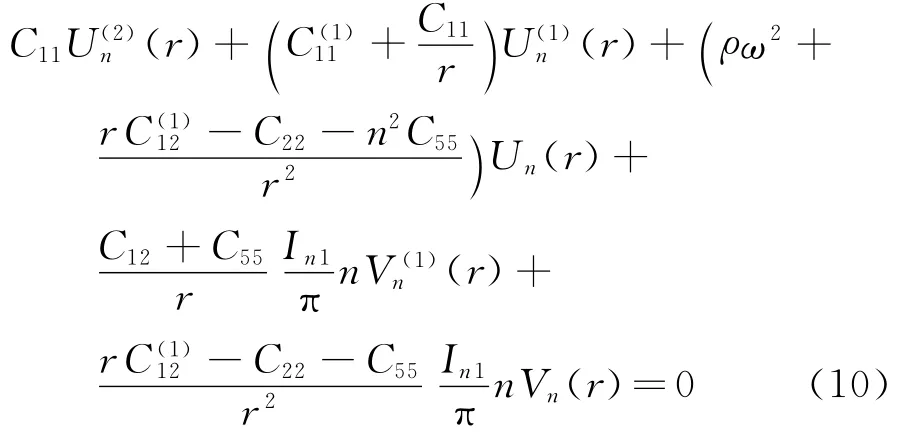


3 控制微分方程的无量纲化及其DQM离散
对方程(10,11)进行无量纲化处理,

式中 S2L=Ec/[ρc(1-μ2c)],β为环扇形板内外半径比,Ω为无量纲固有频率。另外,FGM环扇形板在环向上采用M个均匀分布的节点,而在径向上采用以插值基函数Lagrange多项式得到的节点,节点数为N。节点的选取形式为
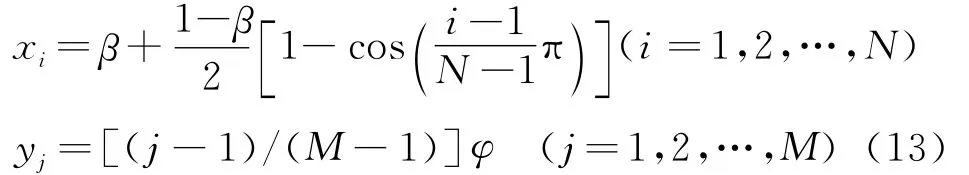
式中 N×M为节点总数。为计算方便,取N=M。参考文献[9,10],由式(13)可求得一阶权系数矩阵以及二阶权系数矩阵,并将式(12)代入式(10,11)
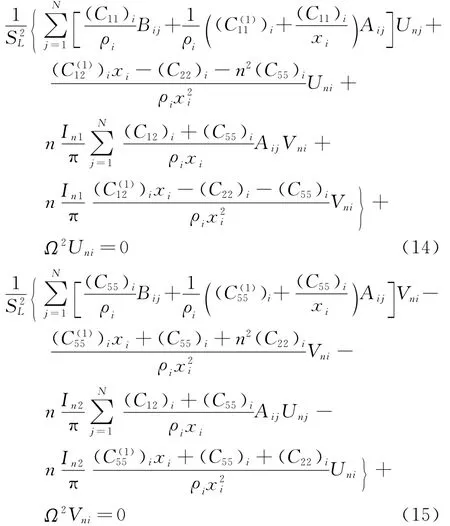
得式中i=2,3,…,N-1,Aij和Bij分别为径向一阶导数的权系数和二阶导数的权系数。
对FGM环扇形板考虑如下三种常见的边界条件:
(1)四周固定(C-C-C-C)
在i=1,N时,

在j=1,M 时,
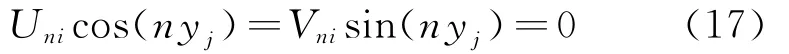
(2)内外固定直边自由(C-F-C-F)
在i=1,N时,

在j=1,M 时,
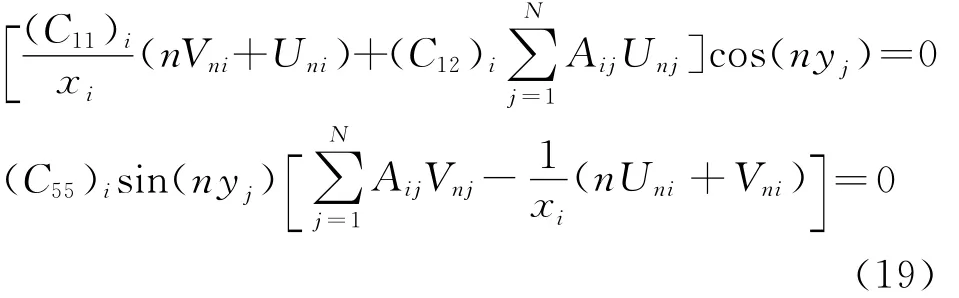
(3)四周自由(F-F-F-F)
在i=1,N时,

4 面内自由振动的特征值问题
方程(14,15)分别与式(16~21)边界条件对应联立,可以得到不同边界条件下FGM环扇形板面内自由振动的边值问题。该边值问题可以用分块矩阵的形式表示[11,12]

式中

对式(22)进行矩阵变换,消去 {wd}后得FGM环扇形板面内自由振动的特征值问题:

式中 [S]= [Sbb]- [Sbd][Sdd]-1[Sdb],[I]为(2 N-4)阶 单 位 矩 阵,特 征 向 量 {wb}描 述 了FGM环扇形板面内自由振动的振型。
5 数值计算与结果分析
计算中FGM 选取由金属材料Ti-4Al-4V和陶瓷材料ZrO2复合而成,其物性参数分别为[13],Em=122.7GPa,μm=0.2888,ρm=4420kg/m3,Ec=132.2GPa,μc=0.3,ρc=3657kg/m3,通过MATLAB编写关于特征值问题的无量纲频率求解程序。表1~表3分别给出了节点数M=N=12,FGM 环扇形板在扇形角φ=π/4,π,2π,内外半径比β=0.2,0.4,环向波数n分别为1,2,3,4,梯度指标p分别为0,1,5,∞时,C-C-C-C、C-F-C-F和F-F-F-F三种边界条件下的前3阶无量纲固有频率。可以看出,在相同边界条件下,当β,p和φ一定时,无量纲固有频率Ω随n的增大而增大;当β,n和φ一定时,无量纲频率Ω随p的增大而减小,这反映了环扇形板材料由陶瓷向金属过渡的特点;当β,n和p一定时,无量纲频率Ω随φ的增大而减少。表1~表3都给出了FGM环扇形板在扇形角φ=π/4和β=0.2时用有限元商用软件ANSYS采用24×24个平面四边形单元计算的固有频率数值结果,与本文方法计算结果吻合良好,且取较少的节点数就能满足精度所需,工作量较小,说明了DQM对于研究本问题的适用性与优越性。
图2分别为FGM环扇形板面内自由振动在C-C-C-C,C-F-C-F和 F-F-F-F三种不同边界条件下,前3阶无量纲固有频率Ω随梯度指标p的变化关系曲线,其中参数p=[0,100],M=N=12,n=1,β=0.2,φ=π/2。可以看出,当p小于10时,Ω随p的增大而减小;当p大于10时,Ω随p的增大而缓慢减小且趋于不变。这同样反映了环扇形板材料由陶瓷向金属过渡的特点。
图3分别为 C-C-C-C,C-F-C-F和 F-F-F-F三种边界条件下,FGM环扇形板在不同环向波数时第1阶无量纲固有频率Ω随梯度指标p变化的关系曲线,其中参数M=N=12,β=0.2,φ=π/2。可以看出,当n,φ和β一定时,第1阶无量纲固有频率Ω均随着梯度指标p的增大而减小,且逐渐趋于常数。当p,φ和β一定时,第1阶无量纲固有频率Ω随着环向波数n的增大而增大。
图4分别给出了FGM环扇形板面内自由振动在C-C-C-C,C-F-C-F和 F-F-F-F三种不同边界条件下,第1阶无量纲固有频率Ω随参数β的变化关系曲线,其中参数β=[0.1,0.6],M=N =12,n=1和φ=π/2。可以看出,当p一定时,第1阶无量纲固有频率Ω随内外半径比β的增大而单调增加;当β一定时,第1阶无量纲固有频率Ω随p的增大而减小,减小程度由明显趋于缓慢,当p足够大,Ω趋于常数。β=0时,FGM环扇形板的面内自由振动退化为FGM扇形板的面内自由振动。可见本文的分析方法也可以用于求解FGM或均匀材料环扇形板以及扇形板等薄板结构的面内自由振动问题。

表1 FGM环扇形板面内自由振动的无量纲频率Ω(C-C-C-C,M=N=12)Tab.1 Dimensionless natural frequenciesΩof in-plane vibration for FGM annular sector plates(C-C-C-C,M=N=12)

表2 FGM环扇形板面内自由振动的无量纲频率Ω(C-F-C-F,M=N=12)Tab.2 Dimensionless natural frequenciesΩof in-plane vibration for FGM annular sector plates(C-F-C-F,M=N=12)

表3 FGM环扇形板面内自由振动的无量纲频率Ω(F-F-F-F,M=N=12)Tab.3 Dimensionless natural frequenciesΩof in-plane vibration for FGM annular sector plates(F-F-F-F,M=N=12)

图2 FGM环扇形板的梯度指标与前3阶无量纲固有频率之间的关系曲线(n=1,β=0.2,φ=π/2)Fig.2 Grade index vs dimensionless natural frequencies of FGM annular sector plates(n=1,β=0.2,φ=π/2)

图3 不同环向波数下FGM环扇形板梯度指标与第1阶无量纲频率之间的关系曲线(β=0.2,φ=π/2)Fig.3 Grade index vs dimensionless natural frequencies of FGM annular sector plates with different circumferential wave number(β=0.2,φ=π/2)

图4 不同梯度指标下FGM环扇形板内外半径比与第1阶无量纲频率之间的关系曲线(n=1,φ=π/2)Fig.4 Internal and external radius ratio vs dimensionless natural frequencies of FGM annular sector plates with different grade index(n=1,φ=π/2)
6 结 论
基于平面线弹性理论,推导得到FGM环扇形板面内自由振动的运动控制微分方程,并进行无量纲化,用二维DQM将运动控制微分方程及其边界条件在FGM环扇形板的环向和径向离散,数值求解得到FGM环扇形板面内自由振动的无量纲固有频率。扇形角为!/4时的部分计算结果同有限元商用软件ANSYS的计算结果进行了比较,结果一致,说明分析方法有效。最后考察了不同边界条件下FGM环扇形板的材料梯度指标、内外半径比以及扇形角对于无量纲固有频率的影响。得到以下主要结论。
(1)随着DQM的节点数的增大,计算结果很快收敛,而且数值稳定性较好。
(2)在改变材料梯度指标p时,FGM环扇形板的无量纲固有频率Ω随着梯度指标p的无限增大而趋于常数。
(3)在改变FGM环扇形板的内外半径比β时,环扇形板的无量纲固有频率Ω随着内外半径比β的增大而增大。
(4)在改变FGM环扇形板的圆心角度φ时,环扇形板的各阶无量纲固有频率Ω随着扇形角φ的增大而减小。
(5)本文方法可以对任意扇形角的FGM环扇形板进行面内振动的无量纲频率进行求解,也可以用来求解FGM或均匀材料扇形板结构的面内自由振动问题。
