密度不同的颗粒在流体中的沉降特性
2018-11-05聂德明
刘 依, 聂德明
(中国计量大学 计量测试工程学院,杭州310018)
1 引 言
颗粒的沉降不仅普遍存在于自然界,而且具有广泛的工业生产背景,是流体力学的一个经典问题。影响沉降的因素很多,如颗粒粒径、流体粘度、颗粒与流体的密度差、颗粒形状和颗粒浓度等,因此对颗粒沉降的研究具有一定的复杂性。从计算的角度来看,目前主要通过直接数值模拟方法对颗粒沉降现象及机理进行研究。
当多个颗粒在流体中一起运动时,其相互作用无论对于颗粒还是流体而言,都至关重要。尤其在流体的惯性不能忽略的情况下,颗粒之间的相互作用往往会对颗粒的运动形态产生显著的影响。DKT(drafting-kissing-tumbling)就是最典型的例子。该现象最早由Fortes等[1]通过实验观察到。Feng等[2]则采用有限元方法模拟了两个圆形颗粒的沉降,其颗粒雷诺数设定为70,其结果重现了DKT现象。此后,Aidun等[3]通过LBM研究了双颗粒在无限长通道中的沉降特性,其结果更为复杂而丰富,研究发现,在较低雷诺数下颗粒的沉降呈现周期性的振动,随着雷诺数的增大,颗粒的运动会出现分岔现象,而进一步增大雷诺数则会转变为随机状态。Verjus等[4]对 Aidun等[3]的结果进行了补充。文献[5-7]研究了中等雷诺数下颗粒的相互作用对沉降的影响。Yacoubi等[5]发现颗粒个数的奇偶性与沉降形态的凹凸形状息息相关,而Nie等[6,7]则报道了多个颗粒在沉降中发生 DKT的选择性组合以及分组现象。Wang等[8]采用LBM对大小不同的颗粒沉降进行了细致研究,重点关注颗粒之间的尺寸差异对DKT的影响。邵雪明等[9]采用拉格朗日乘子/虚拟区域方法,模拟了尺寸不同的双颗粒的沉降过程,结果表明,只有当颗粒之间尺度差异很小时,才会重复进行DKT。曾卓雄等[10]采用数值方法研究了湍流中颗粒碰撞与湍流脉动的关系。胡平等[11]采用LBM研究了倾斜通道内的多颗粒沉降特性,发现当倾斜角处于特定的范围内时,会出现后一个颗粒超越前一个颗粒的现象。陈荣前等[12]采用LBM对双颗粒沉降的动力学进行了分析,揭示了中等雷诺数下颗粒沉降的横向受力特性。
综上所述,颗粒之间的相互作用对颗粒的运动起关键作用。Aidun等[3]发现即使对于双颗粒沉降的简单系统,其呈现的动力学特性也极其复杂而丰富。在沉降的诸多因素中,颗粒的密度决定了其惯性,当密度不同的颗粒置于同一个流场中时,其相互作用必定会受到密度差异的影响,可以预测,这种影响在流体惯性存在下会变得极为显著,而轻重颗粒的沉降形态也必定异于相同颗粒的结果。这种差异以何种方式体现,重颗粒是否一定会比轻颗粒沉降快,什么条件下重颗粒才会离开轻颗粒,这在以往的研究中鲜有报道,因此要回答这些问题还必须通过更为细致而具体的研究,这是本文工作的出发点。
2 模型
2.1 物理模型
两个颗粒并列放置于无限长的竖直通道中,通道宽度为L,颗粒直径为d,颗粒密度分别为ρp(左)和(右)。引入一个无量纲参数k来描述颗粒之间密度的差异,即k=(-ρp)/ρf,其中ρf为流体密度,计算中固定为ρp=1.5与ρf=1,且k>0。本文雷诺数定义为Re=U0d/ν,其中ν为流体的运动粘性系数,U0为特征速度,可表示为

式中g为重力加速度,速度选取的规则与文献[5-7]相同,即假定颗粒沉降所受阻力与重力和浮力平衡,且阻力系数为1。其他参数设置如下,d=30,L=5d,颗粒中心间距固定为2d。在物理单位中,d=0.15cm,ρp=1.5g/cm3,ρf=1g/cm3。网格间距和时间步长分别为Δx=5×10-6m和Δt=5×10-6s。为了模拟无限长通道的边界,计算中重颗粒始终距上游边界15d,距下游边界25d,当重颗粒下降一个网格时,计算网格跟着重颗粒向下移动一个网格。以上参数均在格子尺度下进行设置。
2. 2 数值模型
采用单松弛格子Boltzmann方程求解流场,该模型是目前应用最为广泛的一种LB模型,其演化方程为

式中fi(x,t)为流体分子在i方向上的速度分布函数,fi(eq)(x,t)为对应的平衡态分布函数,ci为i方向上的格子速度矢量,τ为无量纲的松弛时间因子。流体的宏观速度u和密度ρf可以通过式(3)求解,

格子模型采用D2Q9格式,离散的速度矢量为
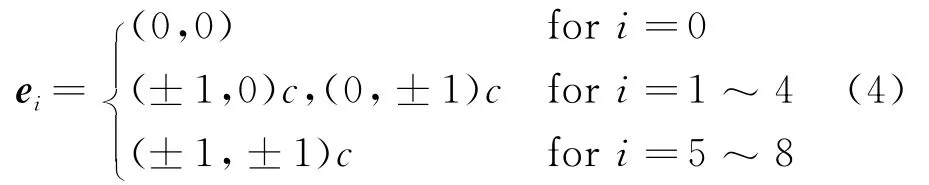
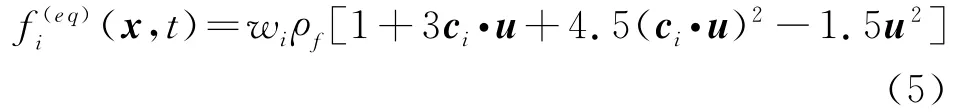
式中 wi为权系数,对于D2Q9为w0=4/9,w1~4=1/9,w5~8=1/36。
对颗粒边界的无滑移条件采用Lallemand等[13]提出的反弹格式来进行处理,该方法可以看作是对标准反弹格式的一种改进。另外,随着颗粒的运动,一些固体节点从t到t+Δt时刻会变为流体节点,而一些流体节点则会变成固体节点,这对颗粒的运动会产生动量变化,从而造成颗粒的受力变化,为了描述这部分力,本文采用Aidun等[14]提出的方法进行处理。
3 验 证
采用通道中双颗粒沉降的DKT结果验证本文计算程序的有效性。参数与文献[15]相同,即颗粒直径d=0.2cm,颗粒密度为ρp=1.01g/cm3,通道宽度L=10d,高度为H=40d,流体密度为ρf=1g/cm3,粘性系数为ν=10-6m2/s,初始时刻双颗粒分别位于(5d,36d)和(5d,34d),分别记为Particle 1和Particle 2。计算采用的网格间距和时间步长分别为Δx=10-4m和Δt=5×10-4s,颗粒之间的碰撞采用了文献[8,15]的弹性力模型。结果如图1所示,双颗粒在沉降过程中发生了典型的DKT现象,本文的计算结果与文献[8,15]符合较好。

图1 双颗粒沉降的DKT结果对比Fig.1 Comparison of the DKT motion for sedimentation of two particles
4 计算结果及讨论
针对5≤Re≤12范围内不同密度差异k的情况进行数值研究。图2给出了颗粒在Re=5时的结果,图中y1和y2分别为轻颗粒与重颗粒的横向位置,且=y1/d=y2/d,t*=tU0/d。可以看出,当k较小时,如k=0或0.01,两个颗粒在沉降中会发生周期性振荡现象,且k越小,振幅越大。值得注意的是,k=0意味着两个颗粒完全相同,然而即使在初始位置对称的情况下,这两个颗粒也不会稳定地沉降,此结果与文献[2]符合。可以看出,当k=0.02时,两个颗粒分别经过初始阶段的振荡后逐渐稳定并最终在通道中心沉降,即y*1=y*2=0。此外,计算结果表明Re=6时的结果与图2相似。
为了更好地对图2所示的周期性运动进行分析,本文通过两个颗粒的水平位置坐标y1和y2构造出相关的相位图,图3分别给出了Re=5和Re=6时的结果。可以看出,每一个k对应的相位图均呈现出一条闭合曲线,意味着两个颗粒做周期性运动。与图5一致,随着k的增大,闭合曲线尺寸逐渐减小。特别地,当k=0时,颗粒振荡的轨迹相位图呈现两条曲线,如图3(a)所示,这是典型的周期倍增现象。当k值逐渐增大时,这种现象消失。此外,轻颗粒的振幅y1明显大于重颗粒的振幅y2,而且轻颗粒几乎均在通道左半边沉降(y1<0),而重颗粒则在通道右半边沉降(y2>0)。
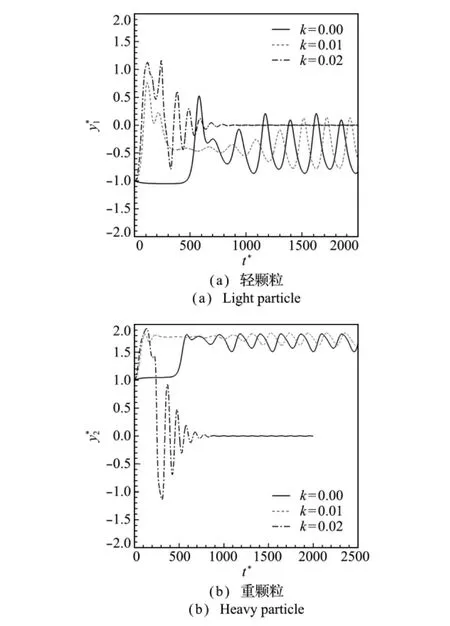
图2 Re=5时颗粒水平位置的变化Fig.2 Horizontal displacements for the particles at Re=5
从图2可以看出,当k较大时,颗粒会在通道中心稳定地沉降,图4给出了Re=5时,0.02≤k≤0.08对应的颗粒沉降流线图。可以看出,当0.02≤k≤0.07时,两个颗粒作为一个整体进行沉降,如图4(a~c)所示,这是由于轻颗粒处于重颗粒的尾流之中,使得阻力减小最终追上重颗粒。当k足够大时,如k=0.08,重颗粒会离开轻颗粒,两个颗粒最终独立沉降,如图4(d)所示。此外必须说明的是,图中所示的箭头表示颗粒的转角,初始转角为垂直方向。

图3 颗粒运动轨迹的相位Fig.3 Trajectory of the particles in phase space

图4 当Re=5时不同k值对应的流线Fig.4 Instantaneous streamlines for different kat Re=5
当雷诺数增大时,颗粒的沉降形态会发生变化。图5给出了Re=7时颗粒的轨迹相位图。可以看出,结果分成了两个部分,k≤0.04时的结果与图3类似;然而k继续增大则出现了另一种沉降形态,即当0.05≤k≤0.07时,轻颗粒在通道右半边沉降(y1>0),而重颗粒则正好相反(y2<0),显然,这两个颗粒交换了初始位置,如图5(b)所示。
当k≥0.08时,颗粒仍然会稳定地沉降。图6给出了Re=7时,k=0.08,0.1和0.11对应的流线图。与图4不同,当k=0.08和0.1时,两个颗粒交换了初始位置,呈稳定的错列结构进行沉降,如图6(a,b)所示。此外,此时重颗粒转动的方向与轻颗粒一致,均是逆时针方向。造成这一现象的原因在于重颗粒靠近壁面而受到较大的壁面排斥力,为了平衡这个力,导致了重颗粒的反常旋转,并由此产生了一个马格努斯力。
当雷诺数继续增大时,颗粒的沉降特性又会发生新的变化。如图7所示,当Re=9时,颗粒沉降的轨迹相位图也可以分成两个部分,但与图5所示的结果不同。当k较大时,颗粒的振动幅度随k的增大而增大,而且明显比k较小时的振动幅度大(注意图中坐标轴的范围),当k=0.09时观察到了周期倍增的现象,如图5(b)所示。此外,还可以看出,此时轻颗粒几乎在通道右半边沉降(y1>0),而重颗粒则完全在右半边沉降(y2>0)。
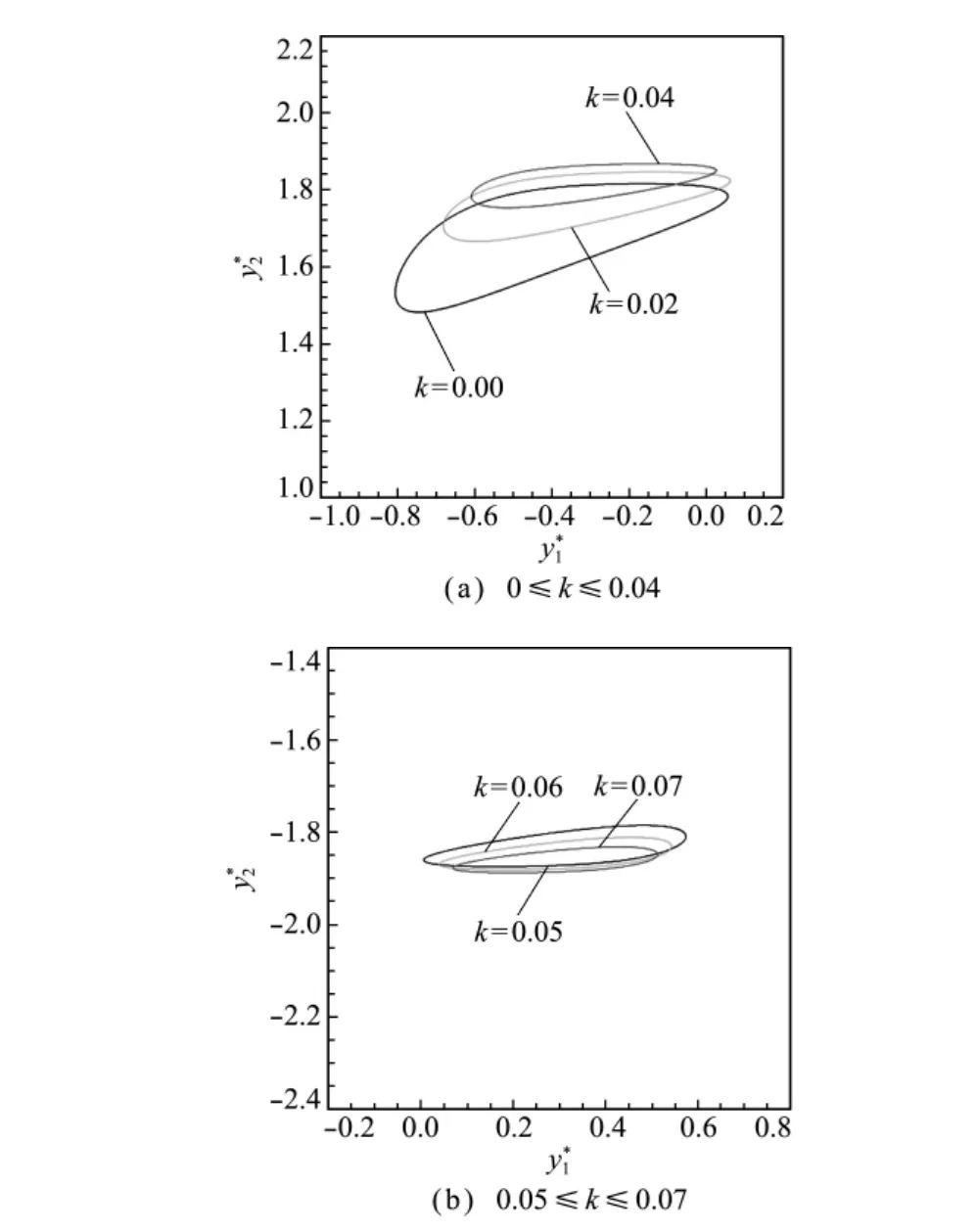
图5 Re=7时颗粒运动轨迹的相位Fig.5 Trajectory of the particles in phase space at Re=7
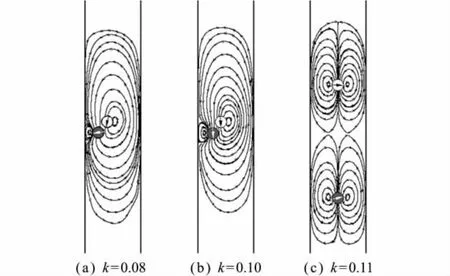
图6 Re=7时不同k值对应的流线Fig.6 Instantaneous streamlines for different kat Re=7
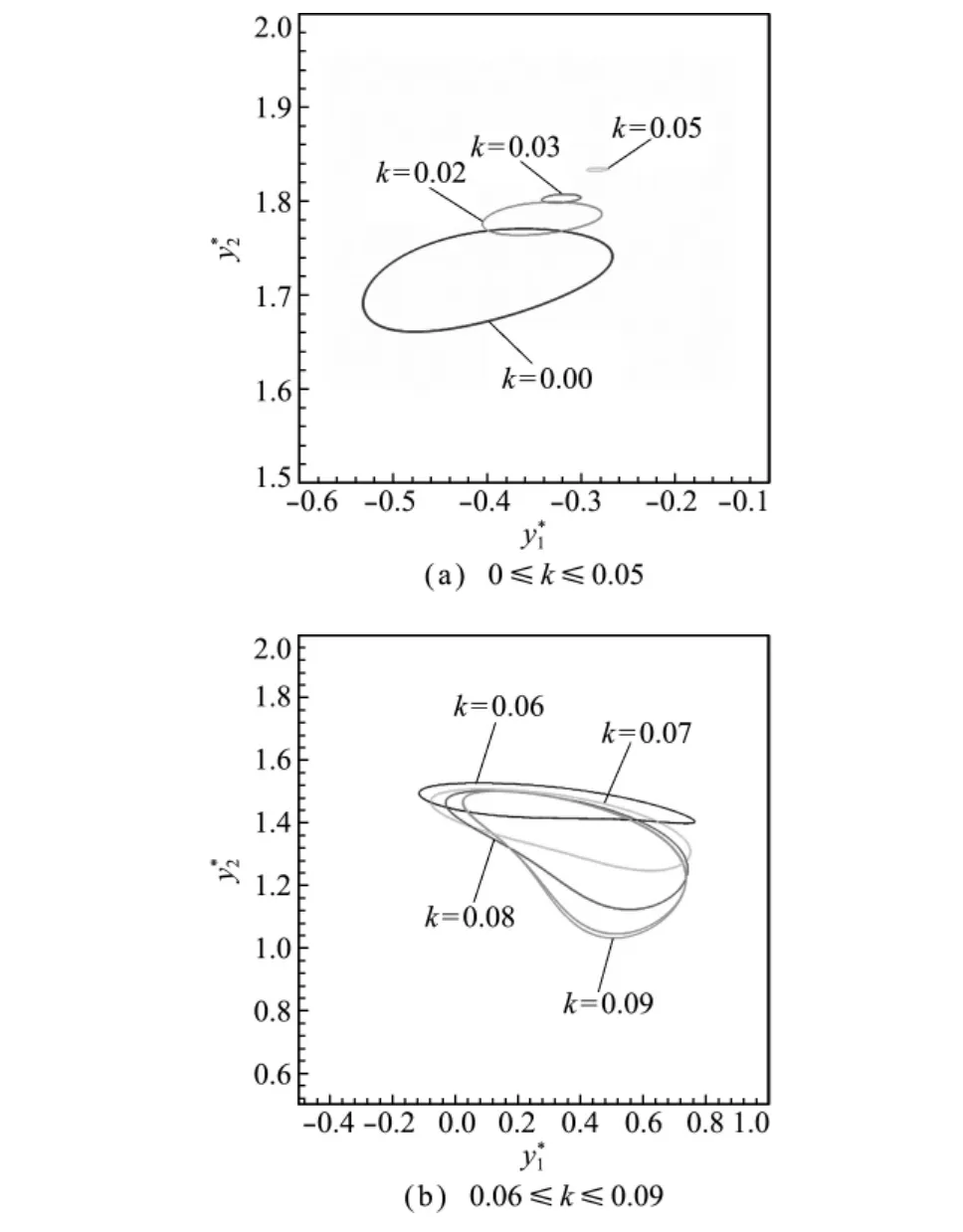
图7 Re=9时颗粒运动轨迹的相位Fig.7 Trajectory of the particles in phase space at Re=9
为了更加直观地观察图7对应的两类周期性沉降运动,图8分别给出了0≤k≤0.05和0.06≤k≤0.08时的颗粒沉降轨迹。每个图截取了两个周期的颗粒位置与转角,相邻的时间间隔为500时间步。可以看出,当k≤0.05时,两个颗粒在沉降中左右轻微振动,相对位置没有明显变化,如图8(a~c)所示。而当k≥0.06时,情况发生本质变化,重颗粒离开壁面并与轻颗粒交织在一起进行沉降,如图8(d~f)所示。当重颗粒从壁面向通道中心运动时,轻颗粒处于其下游因此受到尾流的影响;当轻颗粒加速逐渐靠近重颗粒时,二者之间的排斥作用逐渐增强,当这个排斥力足够大时,两个颗粒又逐渐远离;而当重颗粒靠近壁面时,受到其排斥作用,又向中心运动,如此往复循环,形成了图中所示的周期性运动。这种运动类似于典型的DKT过程,不同的是,由于这两个颗粒密度差异较大,因此颗粒之间没有发生翻转。很明显,当k从0.05增大到0.06时,流体的惯性影响发生了本质的变化,使得颗粒之间的相互作用发生了变化,造成了沉降特性的突变,如图8(c,d)所示。当进一步增大雷诺数即当Re>9时,图7(a)所示的沉降特性消失,只剩下类似于图7(b)的结果,而从图3和图5可以看出,当Re<9时,本文只能观察到与图7(a)相似的结果。由此,可以将Re=9看作是该沉降系统的一个临界雷诺数。
图9分别给出了Re=10和Re=12时对应的颗粒沉降相位图。对于Re=10,仅显示了k≥0.05的结果,这是因为在计算中发现当k≤0.04时,两个颗粒最终会稳定地沉降,沉降的形态与图6(a,b)相似,只是两个颗粒的位置正好相反。从图9可以看出,颗粒振动的幅度随k的增大而增大,尤其是重颗粒的幅度y2变化明显,这与图7(b)的结果相同,但此时相位图出现了类似双钮线的形状,这是因为流体的惯性作用越来越显著,使得颗粒的运动变得越来越复杂。
从上述研究可以看出,在沉降中一定条件下重颗粒与轻颗粒会一起沉降。图10给出了不同雷诺数对应的临界k值即kc,只有当两个颗粒的密度差异大于该临界值时,重颗粒才会摆脱轻颗粒并最终分离。可以看出,随着Re的增大,kc的值先增大后减小,当Re在9附近时kc的值最大,这与上述研究中关于Re=9为临界雷诺数的结论一致。

图8 Re=9时颗粒沉降的轨迹Fig.8 Settling trajectory of particles at Re=9
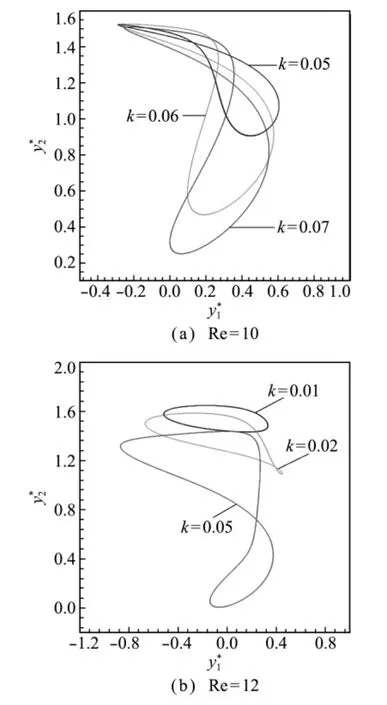
图9 颗粒运动轨迹的相位Fig.9 Trajectory of the particles in phase space for different kat Re=10and Re=12

图10 临界值kc随雷诺数的变化Fig.10 Dependence of the critical value kcon Re
5 结 论
本文采用基于动量交换的格子Boltzmann方法对双颗粒沉降系统进行了直接数值模拟,研究了雷诺数Re=5~12范围内颗粒之间密度差异k对颗粒沉降形态的影响,有以下结论。(1)当雷诺数较小时,即当5≤Re≤8时,颗粒之间的密度差k越小,颗粒周期性振动的幅度越大,当Re=7时,两个颗粒会交换初始位置继续做周期性沉降运动。(2)当雷诺数较大时,即当10≤Re≤12时,由于流体的惯性作用,颗粒的振动幅度显著增大,而且k越大振幅越大;此外,计算发现存在一个临界雷诺数,此时颗粒的沉降形态同时具有以上两种特征。(3)当雷诺数较大时,如果k较小,则两个颗粒会呈现稳定的错列结构,此时重颗粒与轻颗粒的转动方向一致。此外,只有当k大于某临界值时,重颗粒才离开轻颗粒,此临界值随着Re先增大后减小。
