大型风电叶片模具翻转系统设计研究

石鹏飞

(三一重能有限公司，湖南 长沙 410100)

0 引 言

大型风电叶片气动外形由叶片模具保证，而叶片模具的合模位置控制及平稳运动直接关系到叶片模具的操作安全与叶片制造精度。作为大型风电叶片模具关键技术之一的翻转系统，设计定位的准确、翻转运动的平稳是叶片生产制造成功的保证。王宗伟[1]对液压翻转机构进行动力学的分析和优化，乐韵斐等[2]通过MATLAB优化工具箱对风电叶片模具液压翻转机构进行优化，实现风电叶片模具液压翻转机构的参数化优化设计，为液压控制系统和电控部分的设计打下理论基础。冯消冰等[3]从机械、液压、电气三个方面介绍一种全液压翻转机构的设计过程并进行运动优化控制，孙后环等[4]设计了翻转架同步控制系统和算法，刘冰等[5]通过设计改进液压、电气系统，应用PID控制策略，极大改善了多翻转机构的叶片模具翻转过程的平稳性和同步性。

主要从多翻转机构的位置分布对模具的形变影响、翻转机构的运动与载荷分析提供翻转机构的设计思想及优化布置，为大型风电叶片模具的平稳运行提供理论设计基础。

1 翻转系统控制原理

风电叶片模具液压电气控制系统原理如图1所示。翻转机构与拔销机构数量相同，且每一个翻转机构配备一个拔销机构，数量≥2。锁紧机构及顶升机构数量根据风电叶片模具的长度、截面数量、带载顶升重量有关，一般情况下，顶升机构的数量≥4×翻转机构的数量，且前缘、后缘对称布置。

图1 风电叶片模具液压电气控制系统原理图

开模动作实现：控制器通过液压站执行锁紧机构解锁，然后控制顶升机构上升，行程开关检测顶升到位即可执行拔销机构上升动作，拔销机构行程开关检测拔销顶升到位以后，开始执行翻转动作，实时检测翻转油缸压力、各翻转体旋转角度，控制翻转机构平稳运行，直至翻转到位(设定翻转体角度读数为90°)。

合模动作实现：拔销机构行程开关检测顶升到位，控制器通过液压站执行翻转机构合模翻转动作，实时检测翻转油缸压力、各翻转体旋转角度，控制翻转机构平稳翻转至270°。拔销油缸无杆腔开始泄压，行程开关检测到拔销油缸活塞杆下落到位后，顶升油缸无杆腔开始泄压下落，直至顶升油缸下行到位。锁紧机构执行锁紧动作，锁紧油缸压力升至设定值20 MPa，锁紧到位。

2 翻转机构分布位置

翻转机构位置布置对每套翻转机构的承载、上壳体模具的变形有很大影响。以某型号风电叶片模具为例，如图2所示。

图2 风电叶片模具组成示意图

上、下壳体模具由三个翻转机构共同承载实现翻转，翻转支撑点的位置示意图如图3所示，1、2、3号翻转机构支撑点分别为A、B、C点，上壳体模具重心位置为D点。

图3 翻转机构支撑示意图

2.1 超静定求解上壳体模具变形

根据图3，解除支座A，把工件看成是外伸梁CBA，在形式上静定。支座A处等效添加反作用力，载荷包括重力G和多余未知力RA。如图4所示。

图4 翻转机构支撑示意简化图一

在重力G单独作用下，求出截面B的转角为：

(1)

由此引起截面A的向上挠度为：

(fA)G=l1θB1

(2)

重力G单独作用下，截面B转角、截面A向上挠度如图5所示。

图5 翻转机构支撑变形简图1

RA单独作用时，求出截面B的转角为：

(3)

把AB部分看成是整体转动了一个θB2角的悬臂梁，求出截面A的挠度为：

(4)

RA单独作用下，截面B转角、截面A向上挠度如图6所示。

图6 翻转机构支撑变形简图2

叠加(fA)G与(fA)RA得到截面A的挠度。但截面A为铰支座，不应有垂直位移。于是得到变形协调方程：

(fA)G+(fA)RA=0

(5)

综合式(1)～(5)，可解出：

(6)

2.2 三点支撑力载荷计算

根据三铰点支撑分析上壳体模具载荷，如图7所示。

图7 翻转机构支撑示意简化图2

根据力与力矩平衡列出方程组：

(7)

根据式(7)求得：

(8)

该实例中，l1=11.68 m；l2=2.4 m；l3=20.2 m；G=320 000 N，结合式(6)与式(8)求得：

(9)

根据式(9)可知，2号翻转臂承受载荷最大。以L2为变量，代入上述实例值，求得：

(10)

L2值取为0时：

L2取值为2.4时：

由上可知：点A、D、C位置不变，L2值为0时，即2号翻转机构与上壳体模具重心位置重合，RA、RB、RC取得最小值，三组翻转机构承载最小，单独重力作用下上壳体模具的变形最小，位置示意图如图8所示。

图8 翻转机构支撑位置优化分布示意图1

图8中L5为图3中L1和L2之和。以上壳体模具重心G为分割点将上壳体模具切断，取后半段DCE分析载荷，同理，当后半段DCE重心G1位置与3号翻转机构支撑点C点重合时，即L7等于L3，单独重力作用下的上壳体模具尾端变形最小，位置示意图如图9所示。

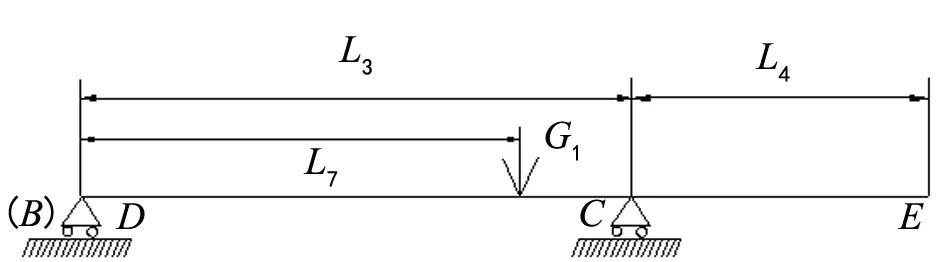
图9 翻转机构支撑位置优化分布示意图2

同理，当前半段DAF重心G2位置与1号翻转机构支撑点A点重合时，上壳体模具首端变形最小。

3 翻转机构运动及载荷分析

3.1 翻转运动过程

翻转机构合模状态下准备开模翻转时，拔销油缸顶升到位，此时翻转油缸有杆腔泄压，无杆腔准备进油，开模初始状态如图10所示。

此时翻转机构翻转体角度传感器设定角度为270°，以旋转中心为原点，画出翻转体上两个油缸连接轴的翻转轨迹如图10虚线圆所示，两个连接轴的初始夹角为θ。执行开模动作，两个翻转油缸无杆腔进油，活塞杆顶升，旋转至第一个死点位置，旋转角度为α，此时1号翻转油缸换向，2号翻转油缸继续顶升。旋转至第二个死点位置，与第一个死点位置夹角为β，2号翻转油缸换向，1号翻转油缸继续下降，翻转及死点位置示意图如图11所示，该实例中θ、α、β均为50°，翻转体翻转到位后传感器角度为90°。

图10翻转机构开模初始状态示意图 图11翻转机构死点位置示意图1.支撑体 2.翻转体 3.1号翻转油缸 4.2号翻转油缸

3.2 载荷分析

上壳体模具施加在翻转机构上的载荷为力矩M=G×L，力臂长度为L。即六个翻转油压缸承受总载荷M，根据翻转机构运动过程可分为三个阶段：

(1) 执行开模→1号翻转油缸换向

运动第一阶段每个翻转油缸均为顶升运动，即活塞杆伸出，速度V为正值。分析1号翻转油缸力臂为油缸伸缩速度V、时间t的函数，计算图示如图12。

铰点OH、OJ为固定值，油缸长度lHJ为随运动过程变化的长度变量：

lHJ=HJ+V×t

(11)

式中：HJ为1号油缸初始长度，V为油缸伸缩速度，t为运动时间。根据三角形△OHJ余弦定理可求得：

δ=arccos[(OJ2+lHJ2-OH2)/2·OJ·lHJ]

(12)

根据直角三角形△OIJ正弦定理可求得1号翻转油缸力臂长度为：

lOI=OJ·sinδ

(13)

2号翻转油缸力臂计算图示如图13所示，同理可求得：

(14)

根据力矩平衡求解三组翻转机构油缸载荷：

F1·lOI+F2·lOK=M/3

(15)

式中：F1为1号油缸载荷；F2为2号油缸载荷。

翻转体旋转运动α角度进入第一个死点位置，此时1号翻转油缸不提供载荷，即F1为0，2号翻转油缸继续顶升，此时2号油缸承受极限载荷，根据式(15)可得：

F2max·lOK=M/3

(16)

图12 1号翻转油缸计 图13 2号翻转油缸 算简图 计算简图

(2) 1号翻转油缸换向→2号翻转油缸换向

通过第一个死点位置之后，1号油缸下降，即活塞杆缩回，速度V为负值。2号油缸继续顶升。翻转体继续旋转运动β角度进入第二个死点位置，此时2号翻转油缸不提供载荷，即F2为0，1号翻转油缸继续下降，承受极限载荷。根据式(15)可得：

F1max·lOI=M/3

(17)

(3) 2号翻转油缸换向→结束开模

通过第二个死点位置之后，两个翻转油缸均为下降运动，即活塞杆缩回，速度V为负值。一起承受上壳体模具载荷。翻转机构油缸载荷参考式(15)。

综合翻转机构三个运动阶段，各翻转油缸载荷计算如下(设定翻转体角度传感器检测旋转角度值为γ)：

(18)

该实例中上壳体模具力臂L长度为2 m，第一个死点位置时，lOK=265 mm，第二个死点位置时，lOI=265 mm。代入式(18)可求得：

(19)

翻转体与支撑体旋转连接轴载荷可根据力的平衡公式求得：

(20)

翻转机构油缸连接销轴通过式(18)载荷进行计算校核，翻转体与支撑体旋转连接轴通过式(20)载荷进行计算校核。

4 结 论

(1) 分析大型风电叶片模具翻转系统控制原理，通过计算翻转支撑点位置对载荷分布、上壳体模具变形的影响，合理分配翻转机构支撑点位置。

(2) 根据翻转机构旋转运动过程计算翻转油缸载荷，理论推导翻转油缸及各连接轴载荷计算公式，为翻转机构结构设计提供理论依据，同时为各铰点进一步优化提供基础。