各向异性海森伯自旋链中的超椭圆函数波解∗

谢元栋

(华南师范大学物理与电信工程学院,广州 510006)

(2018年5月23日收到；2018年7月22日收到修改稿)

1 引 言

对于各向异性海森伯自旋链模型,国内外学者有很多的研究.研究的热点一般偏向于求孤波或孤子等非线性解[1−10],这些工作都基于经典或半经典框架内.众所周知,自旋等于1/2的低维且带交换相互作用的非线性铁磁链中存在孤子解,这些解可以用解析式来表示.但自旋大于1/2的系统中,求孤子或其他非线性精确解析解则很困难.尽管如此,还是可以在霍尔斯坦-普里马科夫表象(HPR)中,应用半经典近似,得到孤子演化的动力学方程,它们最后一般都可化作非线性薛定谔方程或者改进的非线性薛定谔方程,再在一定的参数范围内求其精确解析解.文献[1—10]中的解大部分是孤子或者有一定微扰而振荡的孤子.但一般文献中较少考虑六阶以上的高阶非线性项.因为此时动力学方程变得很复杂.目前,国内外尚未见用椭圆函数来表示这类自旋波.作者在文献[11]中考虑第六阶非线性和无穷型边界条件,首次用椭圆函数来表示这类波动解.

本文在HPR中进一步研究各向异性海森伯自旋链模型.在半经典近似条件下和周期性边界条件下,求出了用雅可比椭圆函数的反函数的组合表示的超椭圆函数波解.

2 自旋链模型及其动力学方程

考虑各向异性,海森伯自旋链模型的哈密顿量可取下列形式[12]:

其中Sl表示第l个离子的自旋；是其z分量；J是交换相互作用；τ是各向异性参数,一般来说是个小量,它的存在使总能量绝对值降低,因而影响动力学方程参数进而影响非线性解的性质；h是外磁场；=±i(i是虚数单位)和满足下列对易关系:

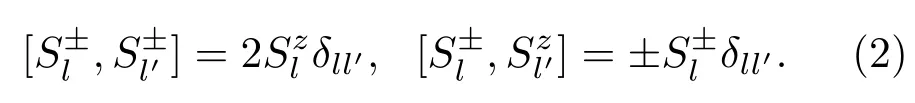
由霍尔斯坦-普里马科夫变换(HPT)[13]并精确到al和的第四阶,得

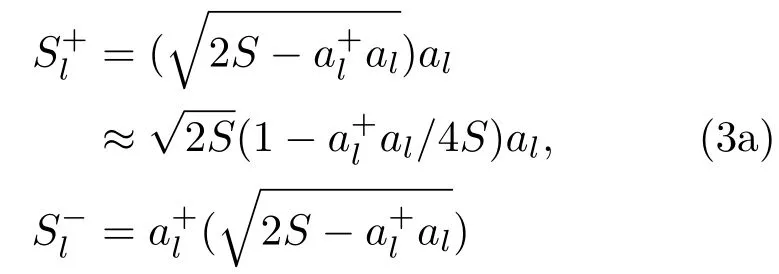
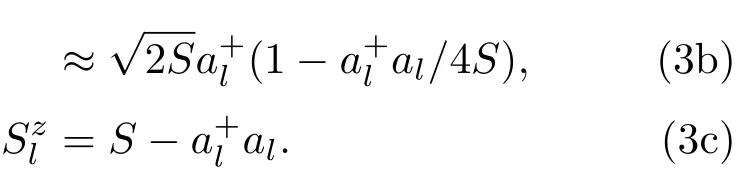
代入(1)式哈密顿量变成

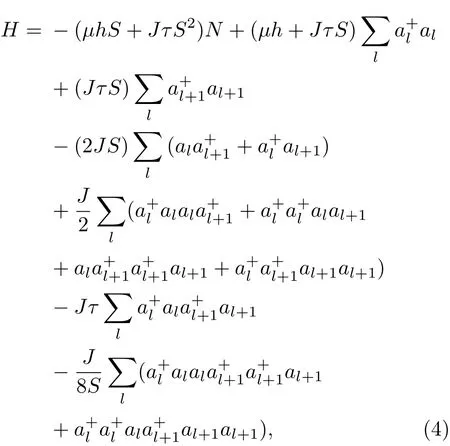
这里N是自旋链中的总格点数.玻色算符al和满足对易关系

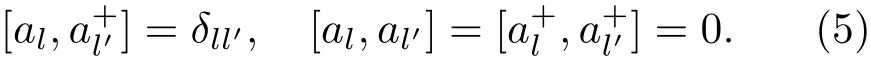
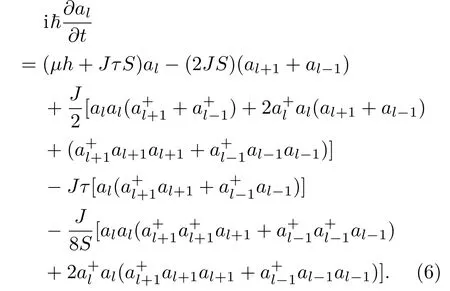
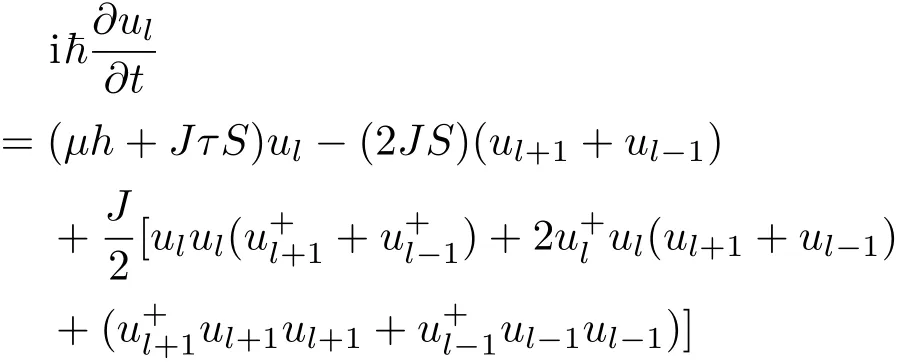
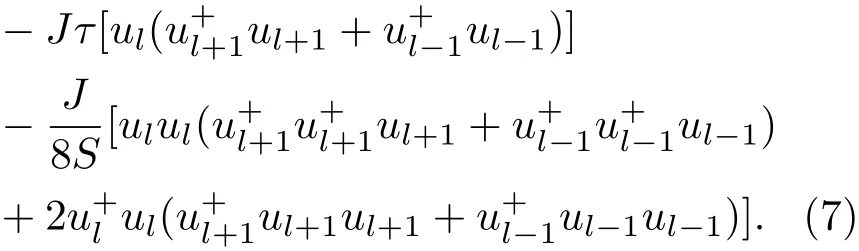
考虑下列连续极限

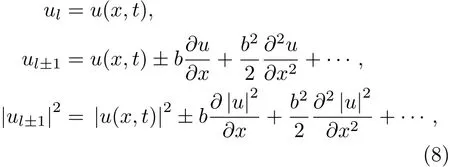
其中b是格点常数.代入方程(7)可以得到

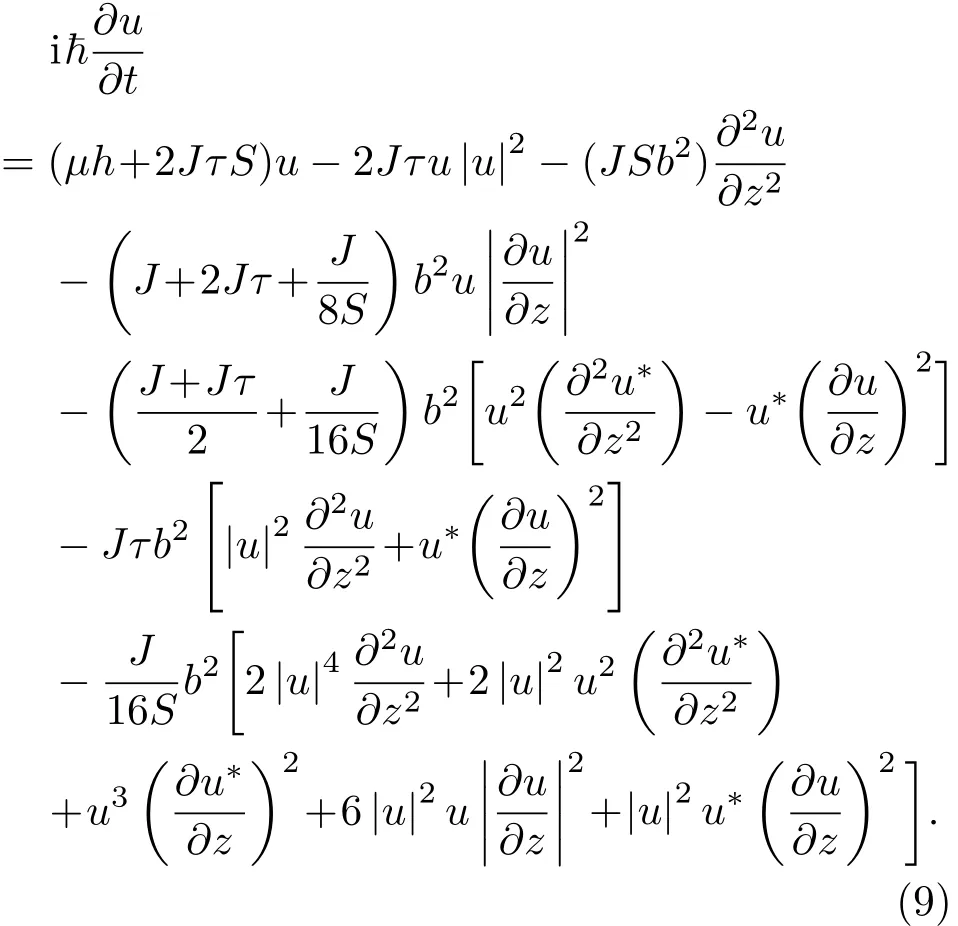
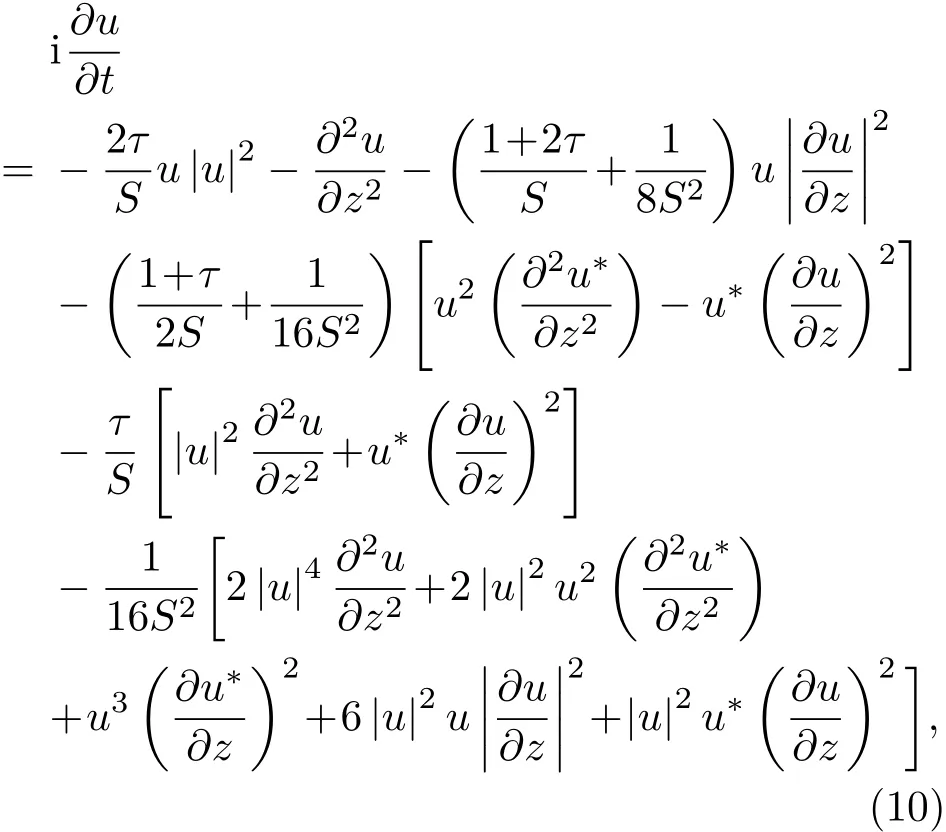
方程(10)中各量都无量纲.

3 超椭圆函数波解

对方程(10)考虑下列形式的解[18,19]:

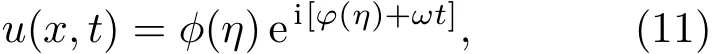
式中振幅ϕ是η=x−vt的实函数,x和t分别是坐标和时间变量,v是波传播的速度；φ(η)是相位,也是η的实函数.把(11)式代入方程(10),考虑到各向异性系数τ很小,即τ≪1时,可以得到下列两个衍生方程:

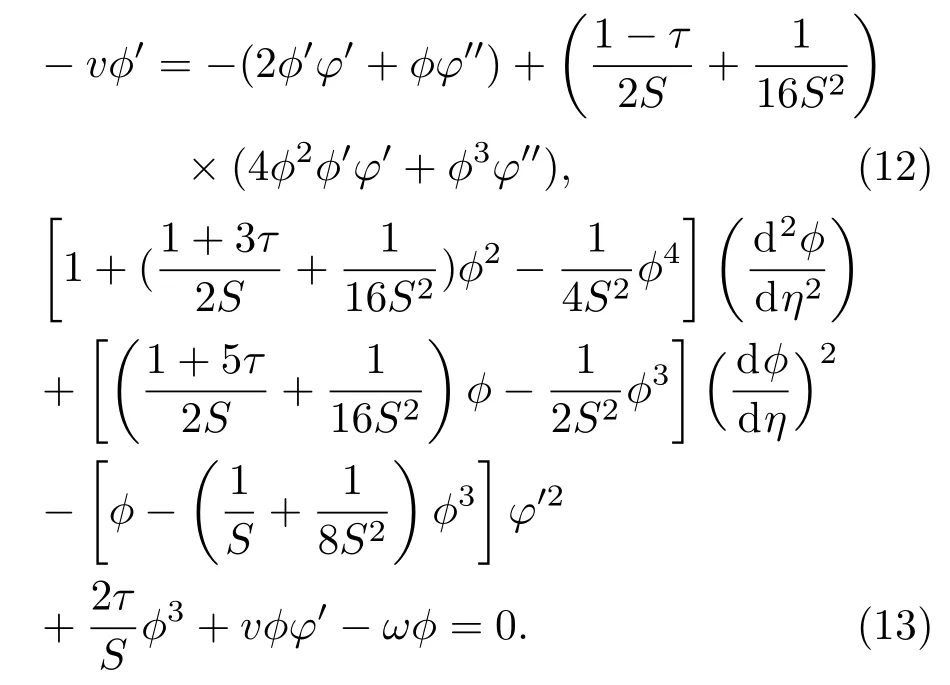
方程(12)可积,对其积分一次得到

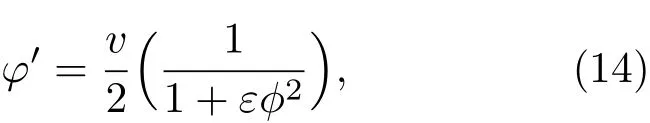
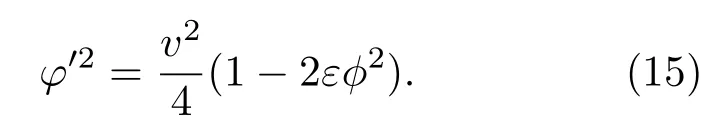
把(15)式代入(13)式,忽略一、二阶导数前面ϕ2以上的小量,并整理得

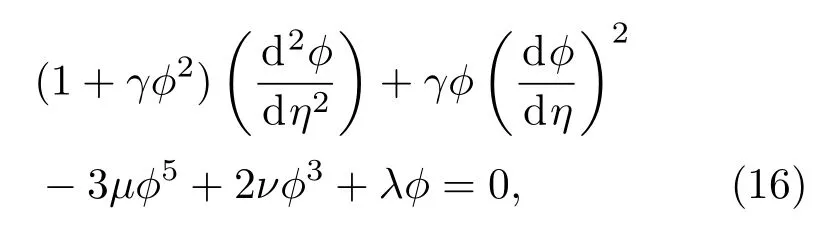
其中

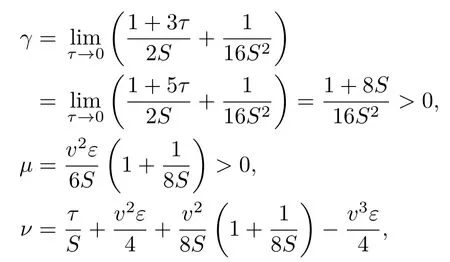
可见,精确解析解是各向异性参数趋于零时的极限.对方程(16)两边积分一次,得

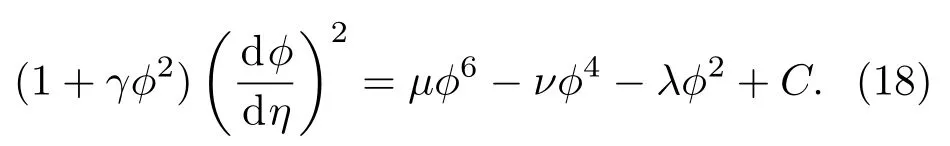
设链长为L,ϕ满足周期性边界条件,即

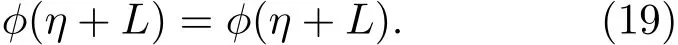
故积分常数C=0. 令y= ϕ2,⇒ y′2=4yϕ′2,则方程(18)变成

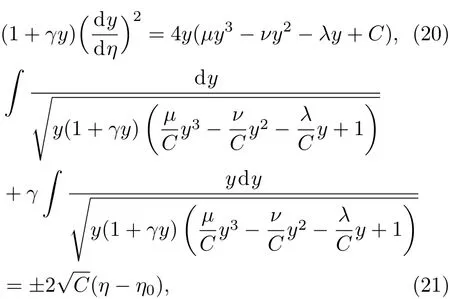
其中初始值η0=x0−vt0.上式左边两项可表示为超椭圆积分,可用雅可比椭圆函数的叠加来表示[20].

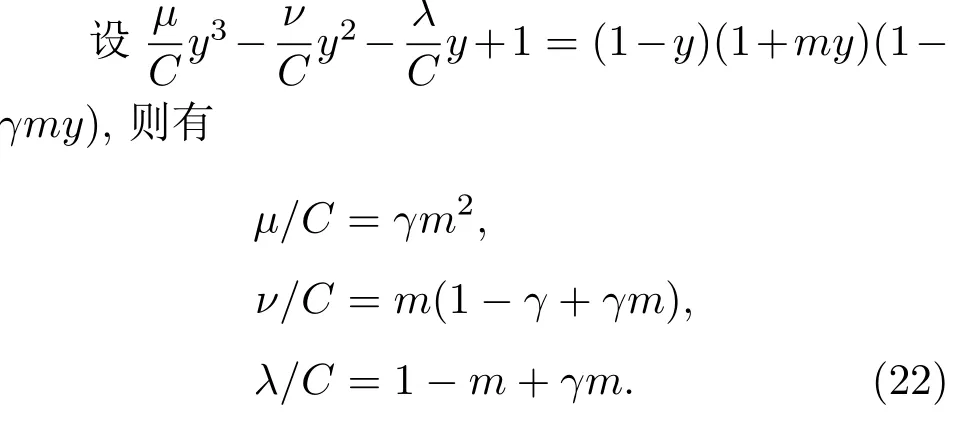
令y=1得C=ν+λ−µ,则有

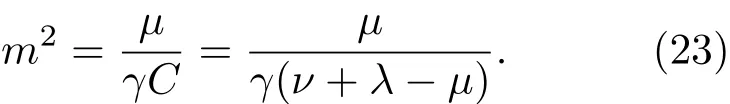
必须满足:ν+λ＞µ.当＜γ时,则方程(21)可写成

方程(24)有解如下:

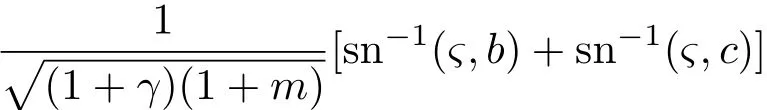
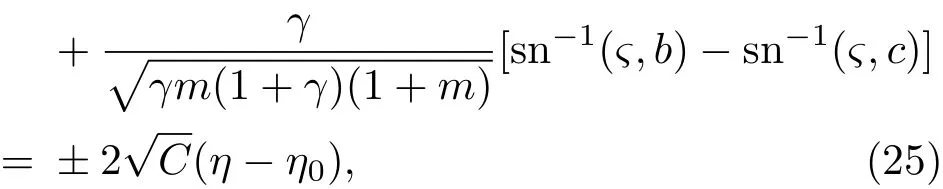
其中sn−1(ς,b)为椭圆正弦函数sn(ς,b)的反函数,且有

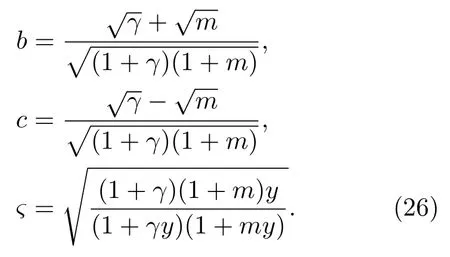
(25)式可整理成

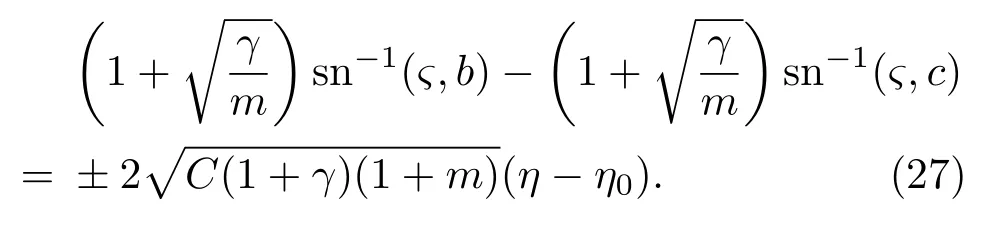
当＞γ时,只需在(26)式中把m,γ互换,(27)式的结果不变.

方程(27)式的图像如图1—图3.从图中可见,超椭圆函数波解是周期解,明显偏离正弦(余弦)波解.当γ增大,亦即各向异性参数τ增大时,偏离正弦波也增大.这是预料中的问题.因为γ很小时,意味着非线性相互作用很小,尚未起作用,其解近似为线性波,但当γ逐渐增大时,非线性项逐步起作用,大到一定程度,其效应就显现出来.如果非线性作用刚好与频散项平衡,就得到孤子解,有偏差时就是超椭圆函数波解.

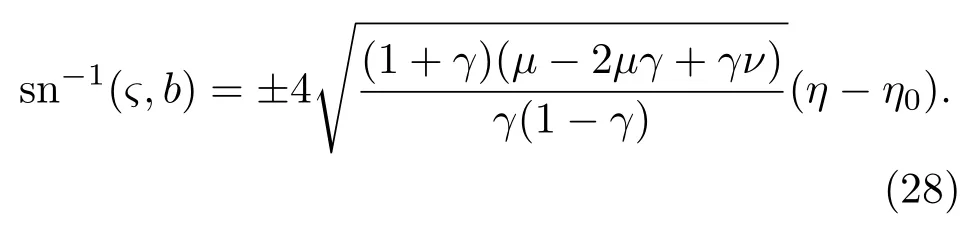
对(28)式考虑周期性边界条件得

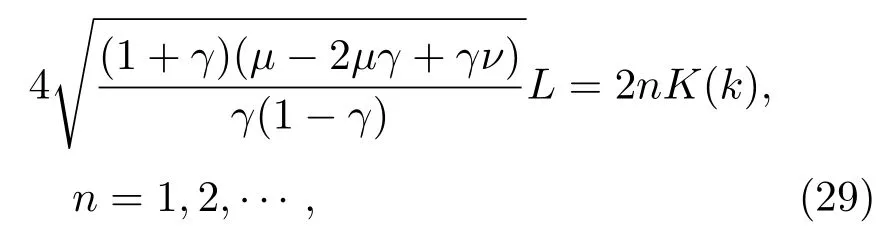
其中K(k)为第一类完全椭圆积分.当γ→1,m→1时,snς→ tanhς,(28)式变为

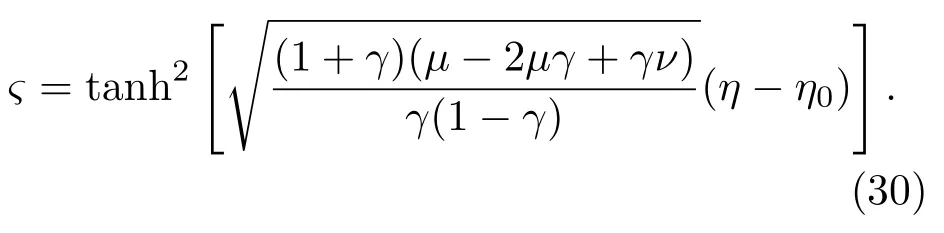
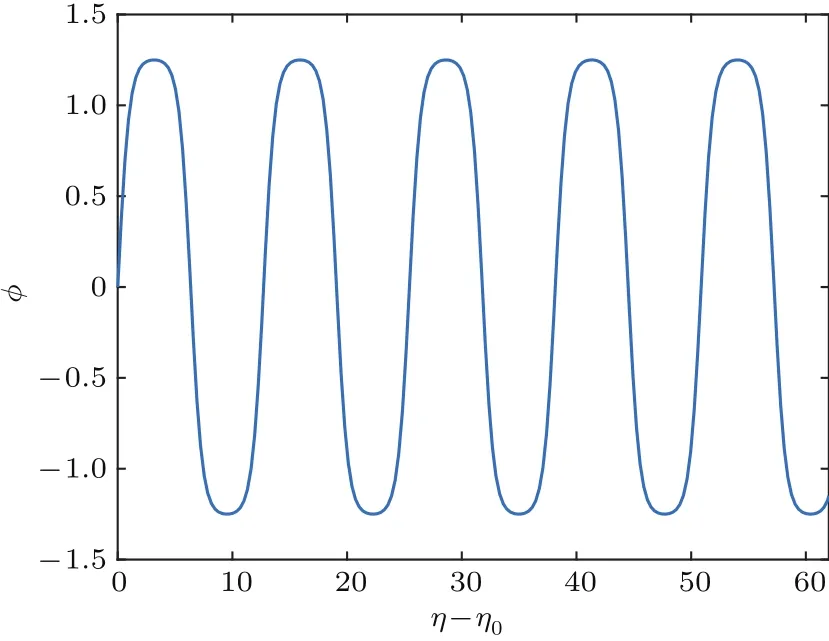
图1 正负概率幅ϕ随变量(η−η0)的周期性变化(取k=0.5,γ=0.6,m=0.6)Fig.1.Periodic variation of probability amplitude ϕ with variable(η − η0)for k=0.5,γ =0.6,m=0.6.

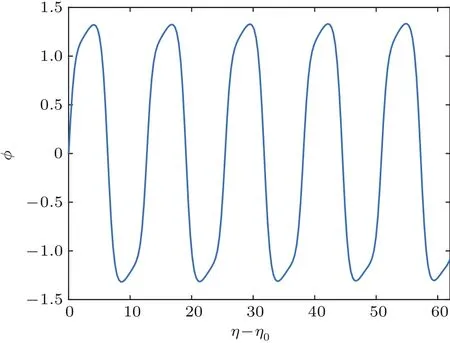
图2 正负概率幅ϕ随变量(η−η0)的周期性变化(取k=0.5,γ=0.8,m=0.6)Fig.2.Periodic variation of probability amplitude ϕ with variable(η − η0)for k=0.5,γ =0.8,m=0.6.

图3 正负概率幅ϕ随变量(η−η0)的周期性变化(取k=0.8,γ=0.9,m=0.8)Fig.3.Periodic variation of probability amplitude ϕ with variable(η − η0)for k=0.8,γ =0.9,m=0.8.

由归一化条件∫|u|2dη=1理论上可以得到无量纲能级ω,即积分式满足

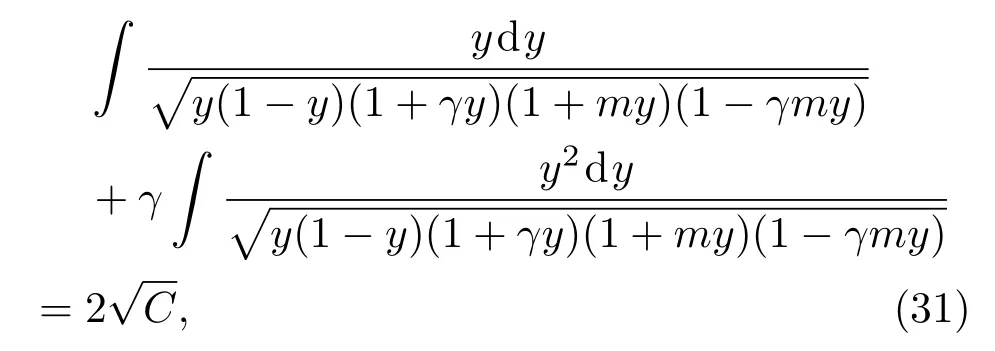
(31)式的第二项不能用超椭圆积分表示.理论上而言,当体系能量取某些值时,波动频散项恰与非线性项作用抵消,这时就出现孤子.能量偏离孤子能量时,就是椭圆或超椭圆函数波.

相位的演化由方程(14)控制.由于振幅ϕ无法表示成η的显函数,因而相位也难用解析式表示.但本文研究的是自旋概率幅的波动,这个虚数最后不会出现.因此,相位对超椭圆函数波实际没有影响,可以不做研究.

4 结 论

在周期性边界条件约束下,带交换相互作用各向异性海森伯铁自旋磁链中存在超椭圆函数波解.这些解可以用第一类椭圆函数的反函数的组合来表示.在极限情况下,其解退化为正弦(或余弦)函数波解,或者能用双曲正切函数表示的波解.由归一化条件理论上可求出自旋链模型的能级,但即使用超椭圆函数也难以表达出来.这些结果对于进一步研究铁磁自旋系统有一定的参考价值.