基于演化博弈论的行人与机动车冲突演化机理研究∗

魏丽英 崔裕枫 李东莹

(北京交通大学交通运输学院,北京 100044)

(2018年3月26日收到；2018年8月10日收到修改稿)

1 引 言

随着我国经济的快速发展,城市居民的出行需求不断增加,道路上行人和机动车流量不断增加,导致行人与机动车的冲突越来越严重,人车事故频发.《中华人民共和国道路交通安全法》第四十七条规定:“机动车行经人行横道时,应当减速行驶；遇行人正在通过人行横道,应当停车让行.机动车行经没有交通信号的道路时,遇有行人横过道路,应当避让.”这为行人过街安全提供了法律保障.但是在实际调查中发现,行人只是在有限的避让范围内才具有优先权,实际中行人和机动车是相互穿越通过冲突区域的.

博弈论作为一门新兴学科,在交通领域中逐渐得到应用.1952年,Wardrop[1]首次将博弈理论引入到交通中,分析出行路径的选择问题,随后大量学者[2−12]开始使用博弈论来研究交通管理、控制及分配等问题.鉴于经典博弈论在应用中被发现存在着假设缺陷、方法缺陷以及实证缺陷等问题[13−19],20世纪90年代发展了演化博弈论的研究工作,并且近年来开始有部分学者将演化博弈论引入到行人过街行为的研究中[20].

本文根据人车冲突实际情景,提出了冲突损失、等待损失、互让损失以及基础收益等概念,并在此基础上建立了行人与机动车的博弈矩阵.引入演化分析范式,建立行人与机动车冲突演化的动力学模型,分析了系统均衡点的位置、稳定性等,以探究“人让车”及“车让人”等形成的机理.本文的研究对于提高道路服务水平、加强道路交通安全、提升交通文明有着重要的意义.

这里需要特别说明的是,本文研究的重点并非针对行人与机动车在一次具体的冲突中是如何做出行为决策的,而在于整个城市的行人与机动车群体经过反复发生冲突,双方为了最大化自己的利益,不断调整自己的行为策略,进行重复博弈,最终达到一种动态平衡的过程.为了定量化表述这种过程,建立了人车冲突演化动力学模型,并用于分析不同条件下人车冲突系统的收敛方向,即是会收敛于“车让人”,又或者是“人让车”等,以及收敛于这些稳定点的速率如何.

2 人车冲突分析

2.1 人车冲突的流程分析

本文讨论的人车冲突是指:在现实的交通环境下,如果行人与机动车双方没有信息交流,无法总是达成谁先行的一致意见,此时,二者都有一定的概率选择通过,即为人车冲突情景.如果行人和机动车双方根据人车安全的前提,不需要博弈很容易就能够达成谁先行的共识,此时认为没有冲突.如图1(a),车辆距离行人太近,行人和机动车根据当前速度和距离一致判断行人通过显然是绝对不安全的,即双方很容易就达成了车辆先行的一致,此类情况在本文中认为不发生冲突.如图1(b),车辆距离行人太远,明显行人以正常速度可以安全通过,也不发生冲突.即这两种情形都不是本文认为的冲突情形.

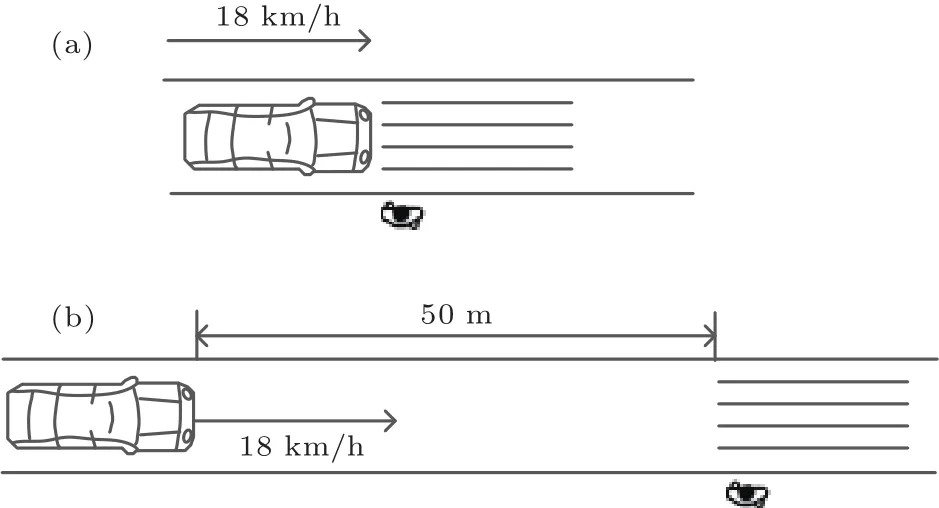
图1 人车不发生冲突的情形 (a)车辆先行；(b)行人先行Fig.1. The situation which there is not conflict between pedestrian and vehicle:(a)Vehicle ahead；(b)pedestrian ahead.

如图2所示,如果人车之间距离介于图1中的两种情况之间,行人将无法准确判断机动车是选择通过还是不通过.因为即使是同样的交通情形,由于机动车驾驶员的个性差异,有些机动车会选择通过,有些机动车会选择不通过,即机动车是以一定概率选择通过的.而机动车以多大概率选择通过,行人只能根据以往的经验判断获知,然后根据判断的机动车通过概率,决策行人自己选择通过的概率.

同样,由于行人也存在个性差异,机动车驾驶员认为行人也是以一定概率选择通过的,进而机动车驾驶员会判断行人的通过概率,据此决策自己选择通过的概率.

既然在图2这种冲突距离下,车辆和行人都是以一定的概率选择通过的,那么车辆和行人就可能同时选择通过,进而有发生人车事故的风险,这就是本文描述和分析的人车冲突情形.即由于不同行人与机动车的特性不同,人车难以根据安全的前提达成先行共识.

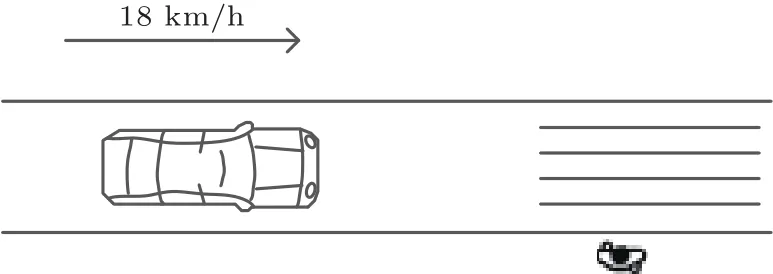
图2 人车冲突情形Fig.2.The situation which there is a conflict between pedestrian and vehicle.

2.2 行人与机动车冲突协调分析

行人与机动车冲突最好的结果是“人让车”或者“车让人”,即行人与机动车之间能达成先行的协调.对于“人不让车,车不让人”或者“人让车,同时车让人”都不是最好的结果,前者易发生事故,后者则影响整体的交通效率.

假设在一次冲突中,行人选择通过的概率为x,机动车选择通过的概率为y,行人与机动车没有信息交流,仅仅根据通过概率决定其是否通过.则行人选择通过,机动车选择不通过的概率为x(1−y),行人选择不通过,机动车选择通过的概率为y(1−x),进而行人与机动车达成先行协调的概率z为上述两部分之和,即

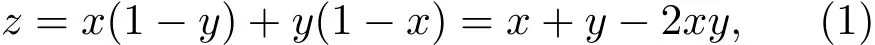
式中,0 6 x 6 1,0 6 y 6 1.

z关于x,y的函数曲线如图3所示,显然z关于平面x+y=1对称.z值最大为1,对应的(x,y)取值为(1,0)或(0,1),其他(x,y)取值越靠近这两组值,对应的z值越大,且沿着x+y=1的平面,z值从最高点下降的速率最慢.

为了便于对图3的交通含义进行分析,下面说明“人让车”,“车让人”以及“人不让车,车不让人”等对应的数学表示.

图3 行人与机动车协调的概率Fig.3.Probability of coordination between pedestrians and motor vehicles.

如果行人选择通过的概率为1,机动车选择通过的概率为0,即(x,y)=(1,0),行人与机动车达成了行人先行的协调,就是所谓的“车让人”.同理,可以得到表1所列的对应关系.其中符号(∼,1)表示x可以取[0,1]中的任意值,y取1；符号(1,∼)表示x取1,y可以取[0,1]的任意值.

表1 数学表示(x,y)对应的交通含义Table 1.Transportation means of the mathematical representation(x,y).

从图3可以看出,(0,1)“人让车”和(1,0)“车让人”两点协调的概率最高,值为1；(1,1)“人不让车,车不让人”和(0,0)“人让车,同时车让人”协调的概率最低,值为0.对于交通管理人员来讲,可以通过采取相关措施,一步步调整行人及机动车通过的概率,从而实现人车冲突系统状态由“人让车”向“车让人”转换.为了保证转换过程中协调的概率尽可能大,在调整时最好能够保持机动车选择通过的概率与行人选择通过的概率之和为1,即x+y=1,这样才能保证调整过程中交通状态尽可能的安全、高效.

3 建立人车冲突演化动力学模型

3.1 基本假设

1)博弈参与主体的集合:机动车(驾驶员)和过街行人.

2)博弈主体策略集合:{通过,不通过}.

3)过街行人与机动车的支付变量.

由于无论如何决策,行人和机动车最终总能通过冲突区,所以过街带来的收益是一直存在的,但是,不同情况下产生的过街时间和其他损失会有所不同.如果设行人、机动车无冲突过街时的基础收益分别为P,V,则行人与机动车选择不同的策略组合,带来的将只是相对于基础收益的损失不同.

如表2,定义行人选择通过,机动车选择不通过时,机动车的损失为其等待损失N；行人选择不通过,机动车选择通过时,行人的损失为其等待损失M；行人和机动车都选择通过时,机动车的损失为其冲突损失S,行人的损失为其冲突损失R；行人和机动车都选择不通过时,机动车的损失为其互让损失K,行人的损失为其互让损失J.另外,行人与机动车发生冲突并不一定是发生事故,所以这里定义的冲突损失并不一定是行人与机动车发生事故对双方造成的损失.

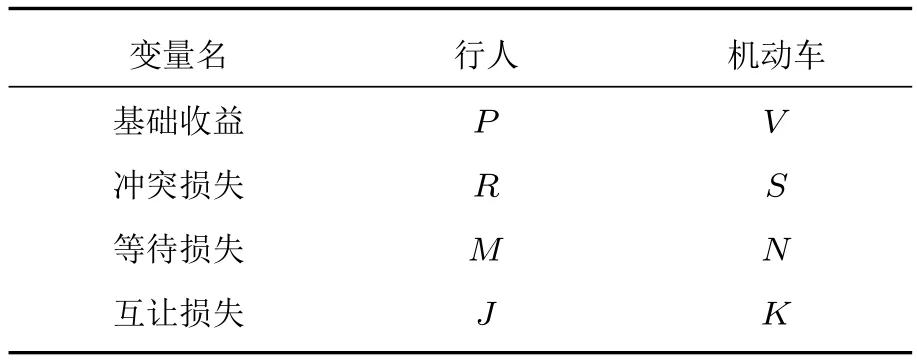
表2 变量定义表Table 2.Definition for variables.

3.2 模型建立

根据上述假设,可以得到行人与机动车的博弈矩阵如表3.

1)行人的期望收益及复制动态方程

行人选择通过的纯策略期望收益Ep1为

行人选择不通过的纯策略期望收益Ep2为

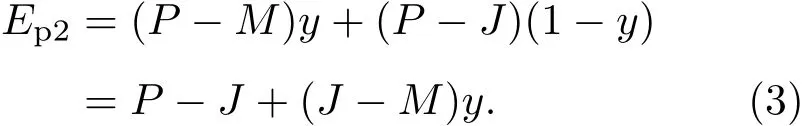
行人以x的概率选择通过,以1−x的概率选择不通过的混合策略的期望收益为

根据(2)和(4)式,得到行人选择通过的复制动态方程为

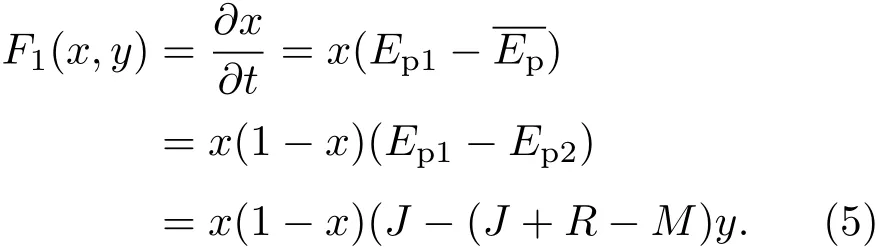
表3 博弈矩阵Table 3.Game matrix.

2)机动车的期望收益及复制动态方程

机动车选择通过的纯策略期望收益Ev1为

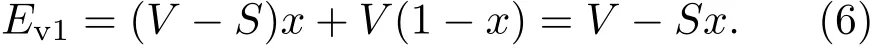
机动车选择不通过的纯策略期望收益Ev2为

机动车以y的概率选择通过,以1−y的概率选择不通过的混合策略的期望收益为

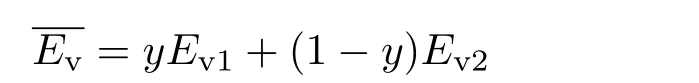
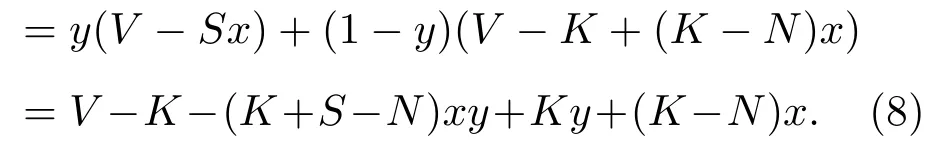
根据(6)和(8)式,得到机动车选择通过的复制动态方程为

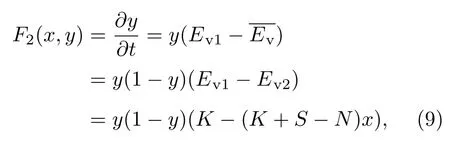
将(5)和(9)式联合起来即为行人与机动车冲突演化的动力学模型.

4 演化均衡稳定分析

4.1 均衡点的相关计算

为求得人车博弈系统的均衡点,根据演化博弈中演化稳定策略的概念和微分方程的相关知识,解由(5)和(9)式组成的关于x,y的二阶微分方程组,如(10)式,即可得到系统的所有均衡点(x∗,y∗).

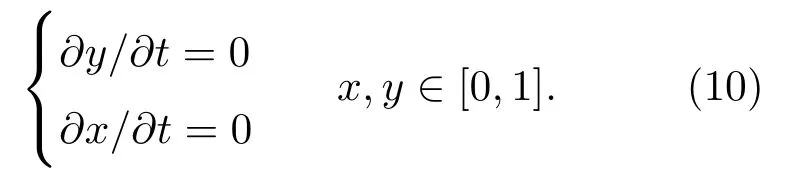
无论支付变量M,R,N,S取何值,二阶微分方程组都有4组确定解(0,0),(0,1),(1,0),(1,1)；当＜R且＜S,另有一组可能解(K/(K+S−N),J/(J+R−M))；特殊条件下R=M(或S=N),还会有无数组特殊解(∼,1)(或(1,∼)).

由(5)和(9)式构成的人车博弈动态系统的雅克比矩阵为

计算(11)式雅克比矩阵的秩和迹如下:

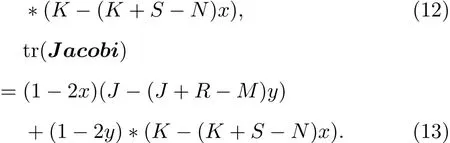
表4 不同均衡点对应的雅克比矩阵的秩和迹Table 4.The rank and trace of the jacobi matrix corresponding to the different equilibrium points.

为了分析均衡点的稳定性,将可能的均衡点全部代入(12)和(13)式中,分别计算人车博弈系统的不同均衡点对应的雅克比矩阵的秩和迹,如表4所列:

4.2 均衡点的稳定性

表5给出了均衡点的类型判别,对于离散系统,当且仅当det(Jacobi)＞0,tr(Jacobi)＜0时,该均衡点为ESS(进化稳定策略)稳定点.由表4可以看出,博弈矩阵的支付变量相对取值不同,det(Jacobi),tr(Jacobi)的正负符号可能不同,进而根据表5判别均衡点的类型不同.

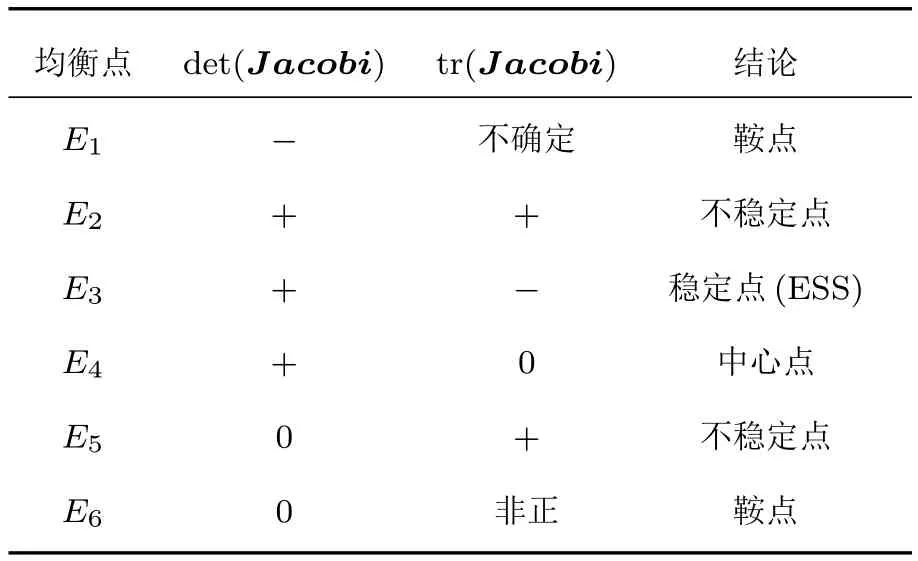
表5 均衡点类型判别表Table 5.The discriminant of equilibrium point type.

决定det(Jacobi),tr(Jacobi)正负符号的因素,主要是博弈矩阵支付变量M与R,N与S的相对大小.考虑M与R的相对大小主要是＜R,＞R,N与S的相对大小可能是＜S,＞S,下面将二者组合成4种情况分类讨论不同情况下均衡点的类型.

这里首先简单讨论M与R,N与S组合成的4种情况对应的现实交通意义.

当过街行人流量比较小,从机动车的角度,由于行人流量小,机动车让当前等待过街行人先通过,甚至连带后面少数的行人通过之后自己再通过,带来的延误以及其他损失(加减速带来的不舒适感等)相对于与行人发生冲突的损失可能并不高,即机动车的等待损失N小于其冲突损失S,即＜S.

同理,当机动车流量较小时,行人让当前即将通过的机动车先通过,甚至连带车辆后面几辆车紧随通过之后自己再通过,带来的延误相对于与机动车发生冲突的损失也并不高,即行人的等待损失M小于其冲突损失R,即＜R.

另一方面,当过街行人流量非常大,从机动车的角度,由于行人流量非常大,机动车如果让当前等待过街的行人通过,后续会有很多行人连续紧随通过,给机动车带来延误可能非常高,再结合其他损失,最后可能高于与行人发生冲突的冲突损失,即机动车的等待损失N大于其冲突损失S,即＞S.类似地,从行人的角度分析可以得到相似的结论,即行人的等待损失M也可能大于其冲突损失R,即＞R.这就说明下文讨论M与R,N与S组合成的4种情况都对应有现实的交通意义.

下面开始讨论4种分类条件下均衡点的稳定性.

1)＜R且＜S

行人的等待损失小于其冲突损失,机动车的等待损失也小于其冲突损失,类似于博弈论经典模型之“性别之战”.此时,系统有5个均衡点:(0,0),(0,1),(1,0),(K/(K+S−N),J/(J+R−M)),(1,1).

表6 ＜R且＜S时的均衡点类型判断Table 6.The discriminant of equilibrium point type when ＜R and ＜S.

从表6中看出系统有两个稳定点(0,1),(1,0).均衡点(K/(K+S−N),J/(J+R−M))为中心点(混合策略纳什均衡点),(1,1)为不稳定点.对于点(0,0),由表4知,无论M,R,S,N取值,其Jacobi矩阵行列式和迹恒为正,从而点(0,0)永远是不稳定点.也就是说“人让车,同时车让人”是永远不可能稳定存在的,下文将不再重复讨论该点.

下面分别取一组满足当前条件＜R且＜S的值,J=1,R−M=2,K=2,S−N=4,做出不同初始(x,y)值下的人车博弈系统的演化路径图(如图4),分析其演化规律.x,y初始值分别取自向量(0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0),下同.

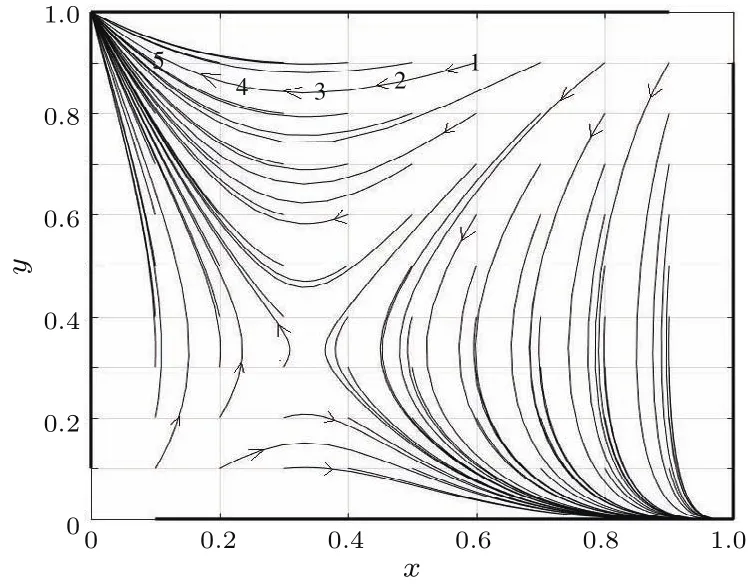
图4 ＜R且＜S时的x-y演化路径图Fig.4.The evolutionary path of x-y when ＜R and ＜S.

这里先以(x,y)初始值取(0.6,0.9)的演化路径为代表分析图4,如图中有数字标号的一条线,其演化方向已在图中标识.1号位置,行人与机动车通过的概率都较大,人车双方的损失以冲突损失为主,且由于行人与机动车的冲突损失均大于等待损失,所以人车将各自降低其通过概率以减少冲突损失,这就有了图中位置1→2→3的演化.在3号位置(x,y)约为(0.35,0.85),此时行人通过概率较低,车辆通过的概率较高.对于车辆,由于行人通过概率较低,其通过概率的调整对冲突损失的增减并不显著,但却会显著影响其互让损失,即互让损失成为其主要损失,所以车辆会提高其通过概率以减少互让损失；对于行人,由于车辆通过概率较高,其通过概率的降低仍可以显著减少冲突损失且不会显著增加互让损失,即冲突损失仍是主要损失,所以行人仍会降低通过概率以减少冲突损失.最终由3→4→5收敛于(0,1),即“人让车”.

总体而言,除了表6中的三个不稳定均衡点之外,所有初始值经过一段时间的演化最终都收敛到(1,0)或(0,1).也就是说,无论行人和机动车的初始通过概率如何,都会向着“人让车”或者“车让人”的方向演化,初始占据优势的行人或机动车,后续的演化更容易积累扩大优势,以更高的概率选择通过；初始处于弱势的博弈主体在演化中会变得更弱,即通过概率不断降低.这里说的行人或机动车占据优势是指其通过概率较高.

这是由于冲突损失大于等待损失,行人和机动车为了降低自己的损失,都会选择尽量不与对方发生冲突,不会出现“人不让车,车不让人”；但是互让损失的存在,又使行人和机动车不至于都不通过,也不会出现“人让车,同时车让人”.经过反复博弈,最终行人与机动车达成“人让车”或者“车让人”的协调.

2)＜R且＞S

行人的等待损失小于其冲突损失,机动车的等待损失大于其冲突损失.此时,系统有4个均衡点:(0,0),(0,1),(1,0),(1,1).计算每个均衡点的局部稳定性如表7.

此时人车博弈系统有一个稳定点(0,1),两个鞍点(1,0),(1,1),特殊的系统初始状态可能会收敛于这两个鞍点.

取J=1,R−M=2,K=2,S−N=−4以满足当前条件＜R且＞S,做出不同初始值下(x,y)的演化路径图,分析其演化规律.

如图5所示,在＜R且＞S条件下,对于任何初始值,人车博弈系统都会以极快的速度收敛于(0,1),除了y=0或x=1时,系统分别会收敛于鞍点(1,0)和(1,1).

这是由于机动车的等待损失大于其冲突损失,选择通过是其严格优势策略,而行人的等待损失小于其冲突损失,行人的最佳对策是选择避让,从而系统存在纯策略纳什均衡,即为(0,1),机动车选择通过,行人选择不通过,“人让车”.

表7 ＜R且＞S时的均衡点类型判断Table 7.The discriminant of equilibrium point type when ＜R and ＞S.

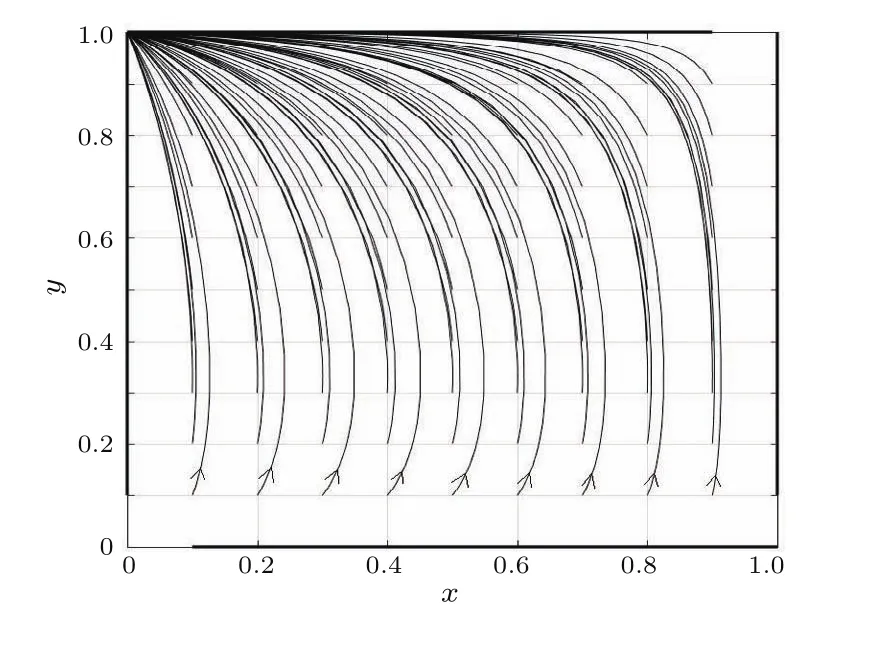
图5 ＜R且＞S时的x-y演化路径图Fig.5.The evolutionary path of x-y when ＜R and ＞S.

a)初始机动车通过概率y=0时,如果机动车通过概率没有任何“突变”,根据(9)式,机动车通过概率y无法向其严格优势策略y=1演化增长,这相当于机动车不知道自己还可以选择通过这种策略,所以只能一直选择不通过,虽然其严格优势策略是通过.机动车选择不通过,行人的最佳对策是通过,所以如果x=0,系统经过一段时间的演化必然收敛于鞍点(1,0)“车让人”.

b)初始行人通过概率x=1时,如果行人通过概率也没有任何“突变”,根据(5)式,行人通过概率x无法向其最佳对策x=0演化,这相当于行人不知道自己还可以选择不通过这种策略,所以只能一直选择通过,虽然通过不是其最佳对策.而机动车通过的概率y必然向其严格优势策略y=1演化,从而系统收敛于(1,1)“人不让人,车不让车”.

另外,收敛于以上两个鞍点“车让人”和“人不让车,车不让人”的条件分别是初始情况下机动车通过的概率为0及行人通过的概率为1,一旦机动车(行人)发生“突变”,这相当于机动车(行人)发现自己还可以选择通过(不通过)这种策略,人车博弈系统将不可逆地收敛于“人让车”,这也比较符合现实的规律.

3)＞R且＜S

行人的等待损失大于其冲突损失,机动车的等待损失小于其冲突损失.此时,系统有4个均衡点:(0,0),(0,1),(1,0),(1,1).

计算每个均衡点的局部稳定性如表8.取J=1,R−M=−2,K=2,S−N=4,做出不同初始值下(x,y)的演化路径图,如图6.由于博弈矩阵变量的完全对称性,此时＞R且＜S与＜R且＞S是完全对称的,不做重复分析.

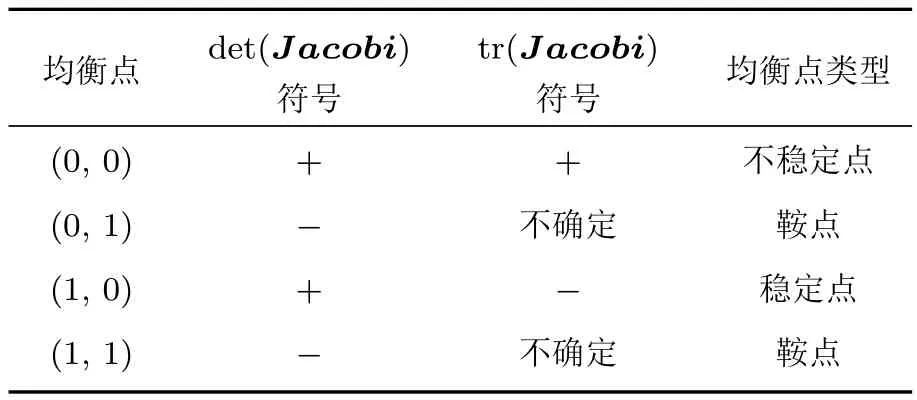
表8 ＞R且＜S时的均衡点类型判断Table 8.The discriminant of equilibrium point type when ＞R and ＜S.

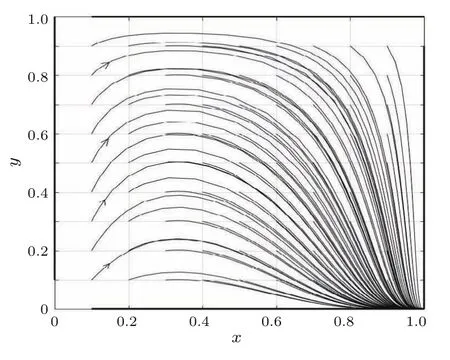
图6 ＞R且＜S时的x-y演化路径图Fig.6.The evolutionary path of x-y when ＞R and ＜S.

4)＞R且＞S

行人的等待损失大于其冲突损失,机动车的等待损失大于其冲突损失.此时,系统有4个均衡点:(0,0),(0,1),(1,0),(1,1).计算每个均衡点的局部稳定性如表9.此时系统有一个稳定点(1,1),两个鞍点(1,0),(0,1).

取J=1,R−M=−2,K=2,S−N=−4以满足当前条件＞R且＞S,做出不同初始值下(x,y)的演化路径图,分析其演化规律.

如图7所示,系统绝大多数的初始值,经过一段时间的演化,最终都会收敛到稳定点(1,1)“人不让人,车不让车”.在初始值x=0且x不发生“突变”时,会收敛到鞍点(0,1)“人让车”；在初始值y=0且y不发生“突变”时,会收敛到鞍点(1,0)“车让人”.

这是由于行人与机动车的等待损失均大于其冲突损失,此时(通过,通过)是惟一的纯策略或混合策略纳什均衡点.绝大多数情况下,系统将向着“人不让人,车不让车”的方向演化.

表9 ＞R且＞S时的均衡点类型判断Table 9.The discriminant of equilibrium point type when ＞R and ＞S.

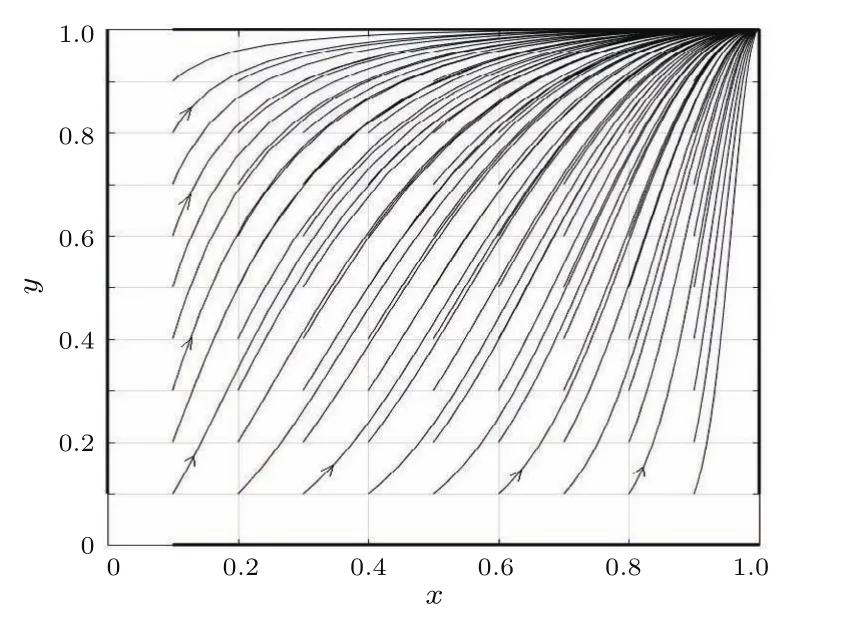
图7 ＞R且＞S时的x-y演化路径图Fig.7.The evolutionary path of x-y when ＞R and ＞S.

5 灵敏度分析

前文讨论了各种情况下人车博弈系统均衡点的位置和稳定性,并分析了系统的演化机理.分析演化机理时,是通过取一组满足当前条件的典型值,做出演化路径图展开分析的.虽然典型值的选取不会影响均衡点的位置和稳定性以及演化路径的基本轮廓,但却会影响着系统收敛于均衡点的收敛速度.为此下文将分析基于博弈矩阵的四个参数J,K,R−M,S−N,对于系统收敛到均衡点的灵敏度.

将(5)和(9)式的行人与机动车通过概率的复制动态方程分别对J,K,R−M,S−N求导得:

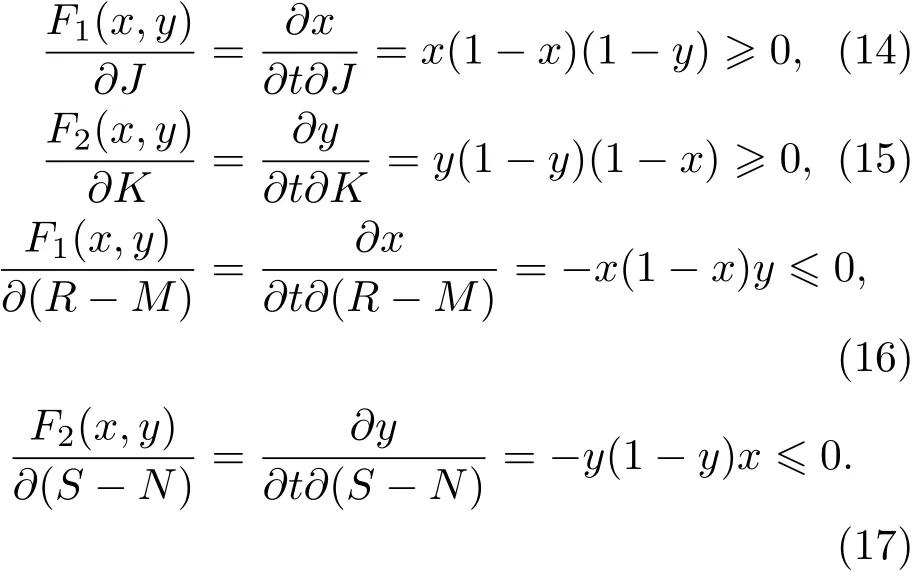
可以看出x,y关于t的变化率是随着J,K的增加而增加,随着R−M,S−N的增加而减小.由于x,y既可能收敛于1,也可能收敛于0,即收敛方向不同,所以J,K,R−M,S−N既可能加快收敛速度,也可能减慢收敛速度.下面将通过Matlab编程做出几种典型情况下,行人与机动车通过概率随时间的演化收敛图,进而分析J,K,R−M,S−N对收敛速度的作用.J,K,R−M,S−N的一组取值只为了说明一种典型,没有其他的特别依据.

为了便于分析观察,本节不再像4.2节取11×11个系统初始值,做出不同初始值下系统的演化路径,而是单方面取系统初始状态(x0,y0)=(0.7,0.3)作为典型,展开仿真分析.由于博弈矩阵中机动车与行人的支付变量是完全对称的,所以如果分析系统初始状态为(x0,y0)=(0.7,0.3)时的演化收敛图,会与(x0,y0)=(0.3,0.7)完全类似.

5.1 J,K的灵敏度分析

为了控制变量,在进行J,K灵敏度分析时,需要固定R−M,S−N的取值.这里R－M取5,而S−N分别取5和－5,以保证能够做出两组演化收敛图,用以分析x,y收敛于0和收敛于1的两种情况.另外,在进行J的灵敏度分析,还要控制K为某一定值,然后J分别取一组不同值,用以分析J的变化对于行人通过概率的灵敏度.在进行K的灵敏度分析时也要进行类似设定.系统初始状态(x0,y0)取(0.7,0.3).

1)J的灵敏度分析

取R−M=S−N=5,(x0,y0)=(0.7,0.3),J分别取1,3,5,7,9,K=1,做出行人通过概率的演化收敛图,如图8(a).取S−N=−5,其他参数不变,做出另外一个行人通过概率的演化收敛图,如图8(b).图中灰色的线由浅到深对应着J值的增大,实线对应的是行人通过概率的演化情况,虚线对应的是同时机动车通过概率的演化情况,横轴是演化时间,纵轴对应行人或机动车的通过概率.

图8(a)是研究S＞N(S−N=5)场景下,行人通过概率的演化关于行人互让损失J的灵敏度图.显然行人互让损失J的增大,使行人通过概率x更快地收敛于1,且过程由曲折变得直接,系统则更快地收敛于“车让人”.即行人互让损失的增加会促进冲突时行人通过概率的增大.

如图8(b)是研究＞N(S−N=−5)场景下,行人通过概率关于行人互让损失J的灵敏度图.显然行人互让损失J的增大,使行人通过的概率x更慢地收敛于0,且过程更加曲折.即行人互让损失的增加会抑制冲突时行人通过概率的下降.

2)K的灵敏度分析

取R−M=S−N=5,(x0,y0)=(0.7,0.3),K分别取1,3,5,7,9,J=1,做出机动车通过概率的演化收敛图,如图9(a).取S−N=−5,其他参数不变,做出另外一个机动车通过概率的演化收敛图,如图9(b).图中灰色的线由浅到深对应着K值的增大,虚线对应的是机动车通过概率的演化情况,实线对应的是同时行人通过概率的演化情况,横轴是演化时间,纵轴对应行人或机动车的通过概率.

图9(a)是研究机动车通过概率关于机动车互让损失K在S＞N(S−N=5)场景下的灵敏度图.可见机动车互让损失K的增加,可能改变机动车通过概率y的收敛方向,能够减缓机动车通过概率收敛于0.即机动车互让损失的增加会抑制冲突时机动车通过概率的下降.

图9(b)是另一个研究机动车通过概率关于机动车互让损失K在＞N(S−N=−5)场景下的灵敏度图.可见机动车互让损失K的增加,加速了机动车通过概率y收敛于1,且这种加速效果后期比较显著.即机动车互让损失的增加会促进冲突时机动车选择通过概率的增大.

图8 行人通过概率的演化收敛图 (a)S−N=5；(b)S−N=−5Fig.8.Evolutionary convergence of pedestrian passing probability:(a)S−N=5；(b)S−N=−5.

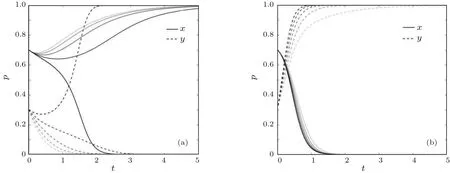
图9 机动车通过概率的演化收敛图 (a)S−N=5；(b)S−N=−5Fig.9.Evolutionary convergence of vehicle passing probability:(a)S−N=5；(b)S−N=−5.

5.2 R−M,S−N的灵敏度分析

类似地,在进行R−M,S−N的灵敏度分析时,需要固定J,K的取值,这里取J=K=5.

另外,在进行R−M的灵敏度分析时,还要控制S−N为某一定值,然后R−M分别取一组不同值,来分析R−M的变化对于行人通过概率的灵敏度.

同样,在进行S−N的灵敏度分析时,也要进行类似设定.系统初始状态(x0,y0)取(0.7,0.3).

下面分析R−M,S−N对应的实际交通意义.R−M,S−N看上去是行人或者机动车冲突损失和等待损失之差,实际上它还有其他含义.

当决策主体面临多个决策时,被舍弃的选项的最高价值即为本次决策的机会成本[17].将机会成本引入到博弈论里,本文定义了如下的机会损失的概念:博弈主体有多个策略,当博弈主体选择某个策略,被舍弃的策略的最高得益与当前选择策略的得益之差即为机会损失.

如表3,分析行人选择通过,机动车也选择通过时,行人的机会损失为P−M−(P−R)=R−M.同样,行人选择不通过,机动车选择不通过时,行人的机会损失为P−(P−J)=J,所以互让损失也是行人选择不通过、机动车也选择不通过时行人的机会损失.

所以R−M,S−N是行人或机动车选择通过,博弈对方也选择通过时,行人或机动车的机会损失.下文为了简化表述,直接将R−M,S−N称为行人或机动车的机会损失.

1)R−M的灵敏度分析

取J=K=5,S−N=−5,R−M分别取−10,−8,−6,−4,−2,0,2,4,6,8,10,(x0,y0)取(0.7,0.3).做出行人通过概率的演化收敛图,如图10.左手坐标系,x轴为演化时间,y轴为机会损失,z轴为行人通过概率.

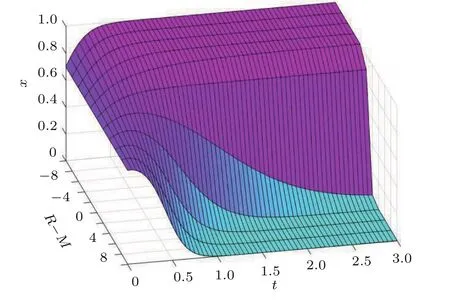
图10 行人通过概率的演化收敛图Fig.10.Evolutionary convergence of pedestrian passing probability.

图10是不同行人的机会损失下,行人通过概率的演化收敛图.当行人通过概率收敛于1时,行人机会损失的增加,减缓了收敛的速度；当行人通过概率收敛于0时,行人机会损失的增加,加快了收敛的速度.即行人机会损失的增加会抑制行人通过概率的上升,促进行人通过概率的下降.

2)S−N的灵敏度分析

取J=K=5,R−M=−5,S−N分别取−10,−8,−6,−4,−2,0,2,4,6,8,10,(x0,y0)取(0.7,0.3).做出机动车通过概率的演化收敛图,如图11.

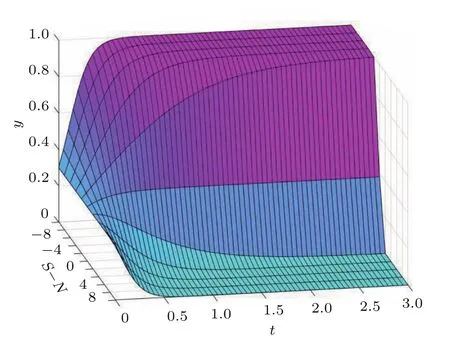
图11 机动车通过概率的演化收敛图Fig.11.Evolutionary convergence of vehicle passing probability.

图11是不同机动车的机会损失下,机动车通过概率的演化收敛图.当机动车通过概率收敛于1时,机动车机会损失的增加,减缓了收敛的速度；当机动车通过概率收敛于0时,机动车机会损失的增加,加快了收敛的速度.即机动车机会损失的增加会抑制机动车通过概率的上升,促进机动车通过概率的下降.

6 总 结

本文在对行人与机动车的冲突情景进行分析的基础上,提出了基础收益、冲突损失、等待损失以及互让损失的概念,据此构建了行人与机动车的冲突博弈矩阵.然后引入演化分析范式,计算行人与机动车选择通过的复制动态方程,建立行人与机动车冲突演化的动力学模型,来分析不同条件下系统的演化方向及演化速率.

表10 不同的冲突损失和等待损失相对大小对应系统的演化方向Table 10.The relative size between con fl ict loss and waiting loss are different,corresponding to different evolution direction of the system.

研究发现,不同的冲突损失和等待损失相对大小,对应人车冲突系统的稳定点及演化方向不同,如表10所列.另外,行人或机动车互让损失的增加对各自通过概率有上升促进和下降抑制作用,而机会损失增加对通过概率的作用则与互让损失恰好相反.

需要说明的是,本文虽为人车冲突演化机理的动力学模型研究,但对交通实践仍具有一定的指导意义.例如,某城市由于历史原因,行人处于交通弱势,在与机动车发生冲突时,总是车辆先行.由于行人冲突损失大于其等待损失,与车辆抢行只能徒增其损失,而车辆处于最大得益状态,亦无改变现状的意愿,所以人车冲突系统处于“人让车”的稳定状态,没有外力干预无法改变现状.此时,如果交通管理部门为提升道路交通文明,希望改变当前的人车冲突状况,实现“车让人”.则可以根据本文建立的模型,制定相关交通法规等改变博弈矩阵某些参数,定向调整人车冲突系统的演化方向为“车让人”,同时避免了法规制定不当,致使系统进入“人让车,同时车让人”的交通效率低下局面,又或者进入“人不让车,车不让人”的事故频发局面.

最后,本文是对于使用演化博弈模型解释人车冲突演化机理的一个初步研究,后续研究仍需选择具体实例标定各参数,以进一步评价模型的合理性.考虑使用延误和风险偏好系数组合来量化损益,确定模型中博弈矩阵各参数.其中延误的确定可以利用交通流间隙理论建立模型计算；风险偏好系数的确定需要调查大量数据,以拟合不同行人及驾驶员的性别、年龄等自然属性与其过街风险偏好的相关关系,例如年轻人过街的风险偏好可能是偏冒险型,其风险偏好系数应为小于1的一个折减系数,而年龄大的人过街的风险偏好可能偏保守型,其风险偏好系数应为大于1的一个扩增系数.模型验证可以选择一个实例人车冲突交叉口,调查相关数据,确定博弈矩阵各参数,根据模型计算冲突演化路径及演化结果,如演化结果与实例交叉口情形相一致,则模型具有一定合理性,进而可以用演化路径图来分析该交叉口的演化过程.