基于系统函数优化的非规则天线阵列综合孔径辐射计亮温反演算法
2018-11-03李育芳胡秋林李青侠
李育芳,胡秋林,李青侠,陈 雄,赵 锋,刘 甡,丰 励
(1.华中科技大学 电子信息与通信学院,湖北 武汉 430074; 2.多谱信息处理技术重点实验室,湖北 武汉 430074;3.上海航天电子技术研究所,上海 201109; 4.湖北工业大学 电气与电子工程学院,湖北 武汉 430068)
0 引言
微波辐射计是接收、处理物体辐射微波信号的专用设备[1-3],是一种新型的全被动探测手段。与主动发射微波信号的雷达相比,其仅被动接收目标发射的微波辐射信号,隐蔽性较强;同时,微波信号能穿透云层等覆盖物[4],受天气影响较小,能全天时、全天候工作,区别金属目标和周边环境的能力强。因此,微波辐射计在目标探测领域得到了广泛的应用。
微波辐射计主要包括实孔径和综合孔径辐射计两类。其中:实孔径辐射计通过机械扫描得到不同角度的辐射能量,其输出电压值与目标场景的辐射能量呈线性关系,只需简单定标、修正即可得到目标场景的辐射亮温,因此,在某种意义上可认为其输出结果就是场景亮温;综合孔径辐射计的技术体制不同于实孔径辐射计,其采用的是干涉测量的方法,系统输出为可见度函数,可见度函数与场景亮温分布是比较复杂的二维积分关系[5-6],如果实际系统中的所有误差均被校正,则综合孔径辐射计输出的可见度函数与场景亮温分布退化为二维傅里叶变换关系[7-8]。因此,综合孔径辐射计的天线阵列常被设计成在空间频率域中均匀采样的规则阵列,如T形阵、Y形阵等。这些规则天线阵列可在空间频率域内产生均匀分布的基线,即对可见度函数均匀采样。此时,将输出可见度采样值进行二维傅里叶反变换即可反演出观测场景的亮温图像。
然而在实际应用中,天线阵列难以排列规则,而非规则排列的天线阵列会在空间频率域内对可见度函数非均匀采样。此时,对可见度采样值直接傅里叶反变换得到的反演亮温图像质量较差。对于非规则天线阵列的综合孔径辐射计,不适合直接采用傅里叶反演算法,因此需引入插值算法[9-10]和迭代算法[11-12],从而有效提高非规则天线阵列综合孔径辐射计的反演精度。但这些算法只是通过单纯的数学方法来实现从非均匀可见度采样值到亮温图像的反演,本身不具备明确的物理含义,也未建立反演误差与非规则天线阵列排布之间的数学模型。
本文提出了基于系统函数优化的亮温反演算法,从非规则天线阵列综合孔径辐射计的系统性能出发,优化系统函数,消除天线阵列非规则排列对反演精度的影响。经系统函数优化处理后,直接对系统输出可见度函数进行傅里叶反变换即可获得精度较高的反演图像。相比于传统的插值算法和迭代算法,本文建立了反演误差与非规则天线阵列排布之间的数学模型,对于理解非规则天线阵列综合孔径辐射计的工作原理、优化设计未来非规则天线阵列具有一定的理论价值和意义。
1 非规则天线阵列综合孔径辐射计的系统函数
综合孔径辐射计利用稀疏天线阵列将阵列中的单元天线成对组成许多具有不同基线的二元干涉仪。例如,由天线i和j组成的二元干涉仪的输出可见度函数表示为
(1)

(2)
式中:B为接收机带宽;Gi,j为系统增益;Hi,j(f)为接收机通道的系统函数。假设综合孔径辐射计的系统误差都能被校正,则理想情况下的可见度函数为
(3)
在实际应用中,综合孔径辐射计的天线阵列尺寸有限,其最大基线也有限,且综合孔径辐射计的基线在空间频率域内为离散分布。这种物理上的限制等效于对输出的可见度函数进行加窗和采样处理。该物理过程用数学公式可表示为
Vmeasure(u,v)=V(u,v)S(u,v;uk,vk)·
WR(u,v)
(4)
式中:Vmeasure(u,v)为综合孔径辐射计输出的可见度,即实际测量的可见度;WR(u,v)为矩形窗;(uk,vk)为空间频率域中的第k个采样点;S(u,v;uk,vk)为采样函数,其表达式为
(5)

(6)
式中:IFT[·]表示傅里叶反变换。将式(4)代入式(6),得
IFT[V(u,v)]*IFT[S(u,v;uk,vk)·WR(u,v)]=
TB*AF(ξ,η)
(7)
式中:“*”为线性卷积运算;TB为观测场景的亮温分布;AF(ξ,η)为综合孔径的阵列因子,其表达式为
AF(ξ,η)=IFT[S(u,v;uk,vk)WR(u,v)]=
(8)
从式(7)可知,综合孔径辐射计的反演亮温为观测场景亮温与阵列因子的卷积。因此,阵列因子也称为综合孔径辐射计的系统函数。
综合孔径辐射计系统函数的旁瓣大小直接影响了反演图像的精度。当天线阵列规则排列时,其在空间频率域中均匀采样,对应的系统函数旁瓣较小,从临近像素点引入的误差也越小。因此,对规则天线阵列综合孔径辐射计直接进行傅里叶反变换,即可反演出精度较高的亮温图像。当天线阵列非规则排列时,其在空间频率域中非均匀采样,对应的系统函数旁瓣较大,从临近像素点引入的误差也较大[13],需通过特定算法处理后才能获得精度较高的亮温图像。一维非规则天线阵列及其系统函数如图1所示。由图1可见,非规则天线阵列综合孔径辐射计的系统函数具有较大旁瓣,其系统性能较差。

图1 一维非规则天线阵列及其系统函数Fig.1 One-dimensional nonuniform antenna array and its system function
2 基于系统函数优化的非规则天线阵列综合孔径辐射计亮温反演
非规则天线阵列综合孔径辐射计反演精度较低,其根本原因是系统性能较差(即系统函数的旁瓣较大)。因此,通过优化其系统函数来提升系统性能,可有效提高非规则天线阵列综合孔径辐射计的反演精度。
根据式(7),非规则天线阵列综合孔径辐射计的反演误差可表示为
TB(ξ,η)*[δ(ξ,η)-AF(ξ,η)]
(9)

(10)
式中:ck为第k个基线上的权重因子。由于优化后的系统函数AFo(ξ,η)需逼近理想的阵列因子,其表达式为
E{[δ(ξ,η)-AFo(ξ,η)]2|c={c0,c1,…,cK-1}}=min
(11)
将式(11)中的方向余弦(ξ,η)进行离散化处理,则式(11)可表示为
‖p-H·c‖2=min
(12)
式中:‖·‖2为欧氏范数;p为向量,即
p=[δ(ξ0,η0)δ(ξ0,η1) …δ(ξm,ηm) …δ(ξM,ηN)]T
(13)
H矩阵可表示为
(14)
其中,
(15)
c为向量,可表示为
c=[c0,c1,…,cK-1]T
(16)
根据式(11)可求解每个基线上的权重因子,即
c=H+·p
(17)
将求解的权重系数乘以对应的基线,直接进行傅里叶反变换,从而反演出观测场景的亮温分布,其表达式为
(18)
式中:F-1为傅里叶反变换矩阵。
然而,由式(18)反演的亮温图像并不稳定,因此需对H矩阵进行奇异值分解,该过程可表示为
(19)
式中:σn为按降序排列的第n个奇异值;un、vn分别为对应的左右奇异向量。因此,H矩阵的广义逆矩阵H+可表示为
(20)
将式(17)、(20)代入式(18)中,则
(21)
从式(21)中可知,H矩阵中包含了许多非常小的奇异值,这些小奇异值会导致反演图像不稳定。实际上,尽管通过误差校正可将硬件系统中的大部分系统误差校正掉,但是硬件系统中还是会存在小部分未校正掉的残差。另外,辐射计系统中还存在难以消除的系统热噪声。这些误差在反演的过程中会被H矩阵中的小奇异值放大,导致最终的反演图像不稳定。为稳定反演结果,需对求解的H矩阵进行正则化处理。经过正则化处理后的权重系数为
(22)
式中:Ntruncated为丢弃的小奇异值数量。因此,正则化处理后的最终反演图像可表示为

(23)

(24)
在求解每个基线上的权重系数时引入了正则化,虽然能稳定反演结果,但会导致反演图像质量的下降。因此,引入了迭代运算,以消除正则化对反演图像质量的影响。
根据数字信号处理的相关理论,式(23)中的线性卷积关系可表示为矩阵乘积关系,即
(25)
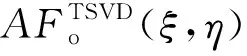
基于式(25)的矩阵乘积关系,具体的迭代过程如下:
1) 经过第n次迭代运算后,反演的亮温图像Tn可表示为
(26)
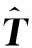
(27)
另外,Tn的初始值为
T0=0
(28)
式(26)中B矩阵可表示为
B=I-A
(29)
式中:I为单位矩阵。
2)计算第n次迭代运算的残差Err=‖Tn+1-Tn‖2,若Err小于门槛值,即
Err2≤ΔT2
(30)
则停止迭代运算,Tn+1即为反演图像。式(30)中,ΔT为停止迭代的门槛值,主要由系统噪声和吉布斯振荡决定。
在整个迭代过程中,式(26)可表示为
⋮
(31)
式中:(Bn+Bn-1+…+I)被称为Neumann序列,当n趋于无穷大时,
Bn+Bn-1+…+I→(I-B)-1
(32)
将式(28)、(29)、(32)代入式(31)中,当迭代次数n较大时,反演图像Tn最终收敛于
(33)
由上述可知,引入的迭代算法是对式(25)进行的求逆计算,而式(25)实际上是系统函数优化后反演出的亮温图像。因此,迭代运算在一定程度上能消除正则化对反演精度的影响,进一步提升非规则天线阵列综合孔径辐射计的反演精度。
3 仿真及结果分析
3.1 理想系统的仿真验证
对理想硬件系统进行计算机仿真,验证本文算法的正确性。为了更清晰显示仿真结果,采用一维天线阵列。假设一随机天线阵列有12个单元天线,均服从均匀随机分布,最大基线长度为30λ。12个单元天线的具体排布位置为{0,5.1,5.5,8.2,11.5,13.7,15.7,17.1,22.3,24.0,27.3,30.0}·λ,如图2所示。

图2 一维随机天线阵列Fig.2 One-dimensional random antenna array
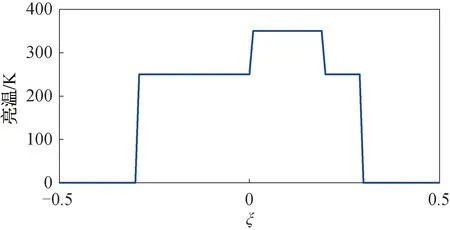
图3 观测场景的亮温分布Fig.3 Brightness temperature distribution of observed scene
观测场景为展源场景,如图3所示。由于仿真阵列中的单元天线是随机排列的,该阵列在空间频率域中非均匀采样,其对应的系统函数旁瓣较大,如图4(a)所示。对仿真阵列输出的可见度直接进行傅里叶反变换,获得的反演图像如图5(a)所示。由图可见,直接反演引入的误差较大。为了优化仿真阵列的系统函数,根据随机天线阵列的具体排列方式,利用式(17)可计算出每个基线上的权重系数,优化后的系统函数如图4(b)所示。将优化后的小旁瓣系统函数替换原先的大旁瓣系统函数,利用傅里叶反变换得到的反演图像如图5(b)所示。由图可见,反演图像质量得到明显改善。

图4 仿真阵列系统函数Fig.4 System function of simulated array

图5 反演图像Fig.5 Reconstructed images
由上述仿真可见,当综合孔径辐射计的天线阵列随机排列时,天线阵列在空间频率域内非均匀采样,导致系统函数的旁瓣较大,且系统函数的旁瓣也不会衰减。因此,反演图像从临近像素点上引入的误差也较大。本文通过优化系统函数,抑制了系统函数旁瓣。将优化后的小旁瓣系统函数替换原有的大旁瓣系统函数,提高非规则天线阵列综合孔径辐射计亮温图像的反演质量。

图6 优化系统函数后,直接傅里叶反变换得到的反温图像Fig.6 Reconstructed images obtained by direct Fourier transform after system function is optimized
3.2 非理想系统的仿真验证
考虑到实际硬件系统中存在多种系统误差和噪声,将本文算法应用在有噪系统中进行仿真验证。综合孔径辐射计的硬件系统不再是理想系统,其接收机的中心频率为1.4 GHz,带宽为25 MHz,积分时间为0.1 s,接收机噪声温度为500 K。由于H矩阵中存在很多小奇异值,会在图像反演过程中放大噪声,因此,如果在优化系统函数的过程中不进行正则化处理会导致反演结果淹没在噪声中,如图6(a)所示。为稳定反演结果,必须对H矩阵进行正则化处理,处理后,基线上的权重系数由式(22)计算。将权重系数乘以可见度函数,直接进行傅里叶反变换可得到反演图像,如图 6(b)所示。对比图6(a)和(b)可知,在优化非规则天线阵列综合孔径辐射计的系统函数过程中必须进行正则化处理,才能得到稳定的反演图像。
虽然正则化处理能稳定反演过程,但会导致反演图像的质量下降。因此,需进行迭代运算。经过120次迭代运算后,反演的亮温图像如图7所示。对比原始图像(见图3)可知,迭代运算处理后的反演亮温图像,质量得到了明显改善。
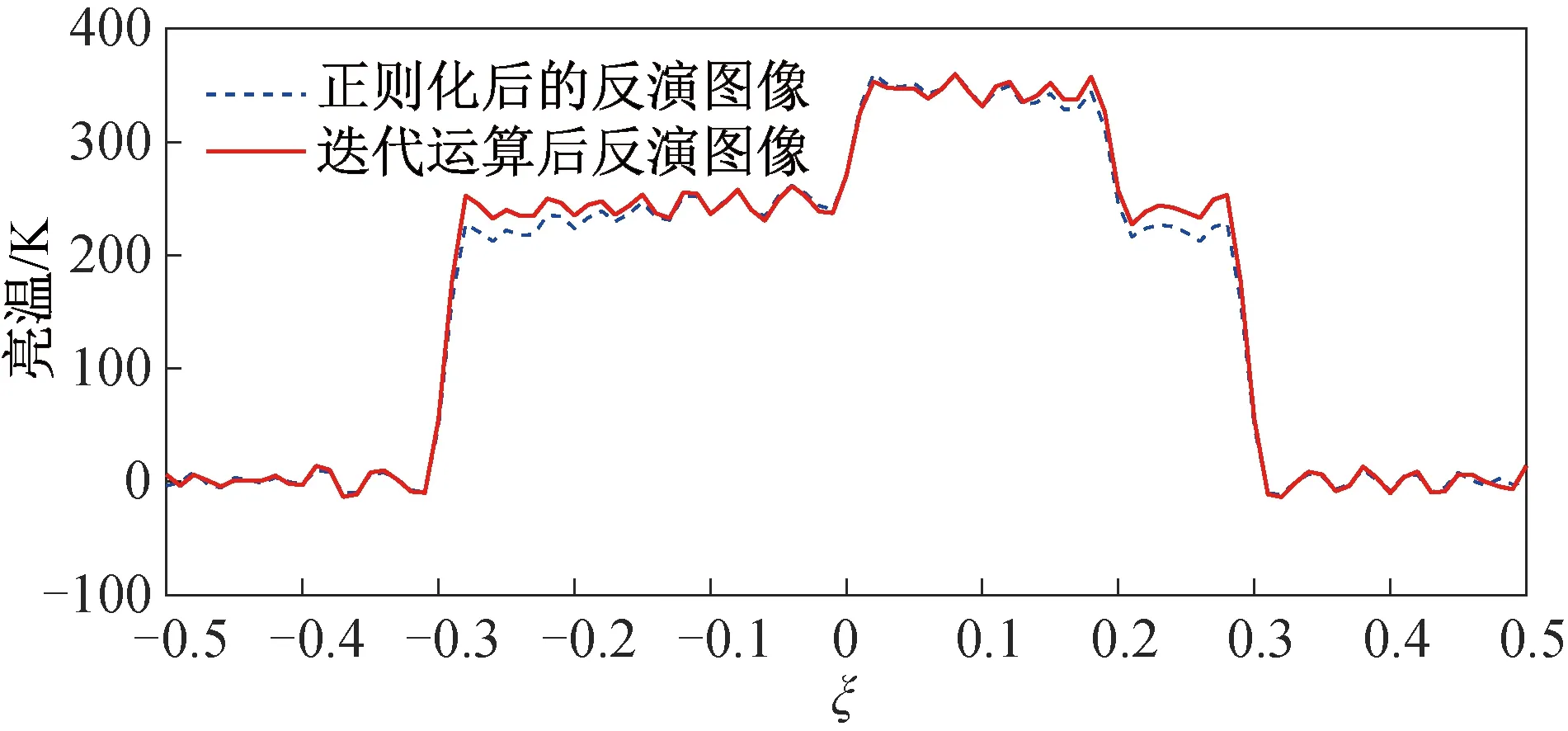
图7 迭代运算与正则化处理后反演图像的对比Fig.7 Comparison of reconstructed images between iteration method and regularization method
仿真结果表明,在非理想系统中噪声会在反演过程中被放大,因此,在系统函数的优化过程中通过正则化的处理,滤掉矩阵H矩阵中的小奇异值,能有效稳定反演结果。但是正则化的处理会导致反演图像的质量轻微下降,在高精度的遥感应用中,反演图像质量是非常关键的。因此,在本文提出的反演算法中引入了迭代算法,通过多次迭代运算达到补偿反演图像质量的目的。
3.3 反演算法对比
将本文算法与G矩阵反演算法进行了对比。仿真场景和仿真条件与前面的仿真完全一致,由于非规则天线阵列综合孔径辐射计的G矩阵条件数较大,因此,在反演亮温之前也需要正则化处理。经过截断奇异值处理后,G矩阵的反演图像如图8所示。由图8可知,本文算法的反演精度与G矩阵类似。由于大型非规则天线阵列难以测量其对应的G矩阵,本文算法可作为测量该类阵列G矩阵的有效手段。
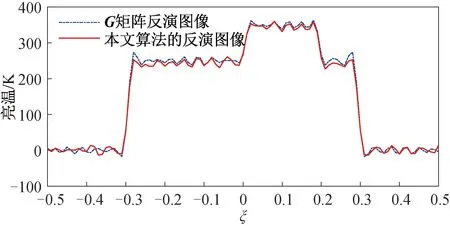
图8 本文算法与G矩阵反演图像的对比Fig.8 Comparison of reconstructed images between proposed method and G-matrix method
4 结束语
本文提出了基于系统函数优化的非规则天线阵列综合孔径辐射计亮温反演算法,通过优化系统函数,消除单元天线非规则排列对系统函数性能的影响,提高反演图像的质量。此外,考虑到实际硬件系统中存在的白噪声和校正后的残留误差会在系统函数优化过程中被放大,影响反演图像质量,因此在系统函数的优化过程中引入了正则化处理,稳定反演结果,但正则化处理会使反演图像质量的下降。为了补偿反演图像质量的损失,在算法中引入了迭代算法。仿真结果表明:对于非理想系统,本文算法能有效提高非规则天线阵列综合孔径辐射计反演图像的质量。将本文算法与G矩阵反演算法进行对比,结果表明本文算法的反演精度与G矩阵大致相当。因此,对于难以测量G矩阵的大型非规则天线阵列,本文算法可作为一种有效反演方法。另外,本文提出的反演算法建立了反演误差与非规则天线阵列排布之间的数学模型,对未来基于小卫星编队的分布式天线阵列的优化研究具有一定的指导作用。
