一种WSN栅栏间隙修复优化方法*
2018-11-02赵小敏毛科技
赵小敏,方 丁,毛科技
(浙江工业大学计算机科学与技术学院,杭州 310023)
栅栏覆盖是无线传感器网络WSN(Wireless Sensor Networks)领域中广泛使用的覆盖模型之一,其目的是研究移动目标试图穿越无线传感器网络保护的区域时被检测到的问题[1-3]。无线传感器网络栅栏覆盖应用广泛,如在国土安全方面,将栅栏部署在边界线可以检测非法越境者;在生态检测方面,将栅栏部署在自然保护区边界用于对入侵物种的检测;在环境保护方面,将栅栏部署在污染隔离区外围检测污染物质的扩散[4]。
目前国内对无线传感器的栅栏覆盖研究已经取得了很大的成果。在栅栏构建和栅栏调度方面,班冬松等人[5]提出了一种1-网格栅栏覆盖优化算法(CBGB),以较低能量构建1-网格栅栏,并提出了一种分治策略的K-栅栏覆盖构建算法,该算法极大地降低了计算以及通信的开销。王超等人[6]提出了一种分区强K-栅栏覆盖构建算法PMNSB,该算法利用最少的节点进行强栅栏的构建,提升了WSN的性能。程建夫等人[7]提出了一种利用移动传感器节点巡逻式的查找栅栏潜在穿越点的栅栏调度方法,该方法通过调度休眠的可移动节点来强化栅栏薄弱点,从而提高了栅栏的覆盖率。在栅栏修复方面,陈业纲等人[8]针对栅栏覆盖优化问题提出一种通过派遣最少移动节点修复栅栏的方法,将带状的目标区域分解成规则域,在每个规则域中实现CBMS算法,降低了栅栏修复时的能耗,但该方法没有考虑可移动节点的移动距离。邓先军等人[9]提出一种混合式的栅栏间隙修复方法,融合了最小最大方案(min-max scheme)和最大生存时间方案(max-lifetime scheme),虽然降低了可移动节点的最大移动距离,但是没有使可移动节点的平均移动距离达到最小,因此修复栅栏时具有较高的能耗代价。戴光麟等人[10]提出了一种利用网络中移动节点修复栅栏间隙的方法,采用基于集合最大流算法计算修复间隙所需的移动节点数量,并利用二分搜索法得到可移动节点距离对应的邻居待修复节点的最短距离,从而使移动节点的移动距离尽可能的减少,该方法虽优化了移动节点的派遣问题,但利用二分搜索法计算移动距离时存在误差,因此移动距离不能达到最短。陈姣燕等人[11]研究了有向传感器节点组成的栅栏出现间隙的问题,通过基于线路的部署策略对传感器节点进行部署从而形成栅栏覆盖,提出一种查找子栅栏以及栅栏间隙的高效方法,并设计了两种栅栏间隙修复算法(SRA算法和CRA算法),有效地提高了栅栏间隙的修复率。
国外无线传感器网络的栅栏部署技术也已经非常成熟。在栅栏构建方面,Santosh Kumar等人[12]首次提出了弱K-栅栏覆盖和强K-栅栏覆盖的概念,通过使用集中式算法快速判断监测区域能否形成K-栅栏覆盖,推导出形成弱K-栅栏覆盖的临界条件。CF Cheng 等人[13]提出一种新型栅栏覆盖方法—目标栅栏覆盖,该覆盖方法对外部入侵和内部目标的突破进行监测,适用于监狱场景中,部署时降低了传感器节点的部署数量,减少了节点之间的信息交换量,从而降低了部署的成本。Kim等人[14]提出了一种优化的强栅栏部署方法,该方法可以检测到任何入侵者进入检测区域,提高了传感器节点检测的准确度。Ashutosh Baheti等人[15]提出了一种集中式算法,通过随机初始化部署传感器节点形成非线性栅栏,减少了所需可移动节点的移动距离,从而降低了整个网络的能耗。栅栏调度方面,Jonathan DeWitt等人[16]提出一种分时调度栅栏的方法,将能量收集纳入到栅栏覆盖问题中,通过节点剩余能量调整栅栏睡眠时间表,由于该方法充分考虑了节点的能耗均衡,因此大大提高了栅栏覆盖的生存时间。栅栏修复方面,Larbi-Mezeghrane等人[17]利用随机部署节点引起的信息冗余,提出一种生成调度集的方法,使用最少的可移动节点修复栅栏实现了K-栅栏覆盖,减少了能耗,增加了网络的生存时间。Nikitha等人[18]提出了一种覆盖间隙修复算法(CGR),该方法通过检测网络中低能量的节点,派遣分布在低能量节点周围最近的可移动节点进行替换,由于替换的过程中采用就近策略,会陷入局部移动距离最短,难以实现修复栅栏的移动距离总和最小,因此修复栅栏的能耗代价并不是最低的。
鉴于上述栅栏间隙修复方法存在修复代价高的问题,本文提出一种WSN栅栏间隙修复优化方法OMBR(An Optimization Method for WSN Barrier Gap Repair),利用KSP(Top-k-Shortest Paths)算法[19]寻找所需可移动节点数量最少的可修复路径,采用匈牙利算法[20]派遣可移动节点去修复栅栏,使可移动节点修复栅栏间隙的移动距离总和最小。该方法能够在花费较小代价(即修复栅栏时所需可移动节点最少,且修复过程中移动距离总和最短)的前提下完成栅栏的修复工作。
1 栅栏间隙修复
栅栏间隙修复方法OMBR的具体思路是首先利用栅栏间隙查找方法获得栅栏中所有间隙的位置和间隙的长度,然后利用静态节点构建可移动节点数量需求拓扑图,接着采用KSP算法寻找可移动节点数量需求拓扑图中的最佳修复路径,最后利用匈牙利算法派遣可移动节点,完成栅栏的修复工作。
1.1 栅栏间隙查找
假设已经通过参考文献[21-23]等提出的栅栏构建方法完成了栅栏的初始化构建工作,但是由于诸多因素的影响,如泥石流对栅栏的冲击、节点自身电量消耗殆尽,此时栅栏会产生间隙,从而导致栅栏有入侵检测的漏洞,如图1所示,左侧栅栏节点ni与右侧栅栏节点ni+1之间出现了间隙,入侵者可穿越栅栏间隙而不被栅栏监测到。
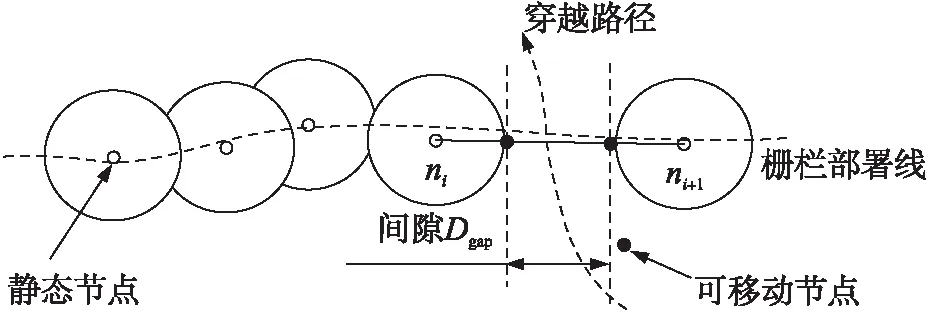
图1 栅栏间隙图
当栅栏出现间隙时,需要定位到栅栏间隙所处位置并对其进行修复。传感器节点部署到监测区域时,一般采用静态节点和可移动节点按一定比例混合的方式部署,且部署的节点能够通过GPS或WSN定位方法获得自身位置,因此为栅栏的修复提供了可能。
由于节点的位置已知,假设传感器节点(静态节点和可移动节点)的感知半径为r,则可根据节点之间的距离判断栅栏之间是否出现了间隙。间隙距离Dgap如式(1)所示。
Dgap=dist(ni,ni+1)-2r
(1)
式中,dist(ni,ni+1)表示节点ni,ni+1之间的欧式距离,r为传感器感知半径。
当Dgap>0时表示栅栏出现了间隙,应该及时查找并进行修复,其中查找方法可根据参考文献[24]中提出的栅栏间隙查找法得到栅栏中所有间隙发生的位置以及间隙的长度。
1.2 构建可移动节点数量需求拓扑图
利用分布在栅栏间隙周围的静态传感器节点构建全连接拓扑图G(V,E),其中V代表分布在栅栏间隙周围的静态传感器节点,E表示两个静态传感器节点之间的边。假设栅栏在节点s,t之间出现了间隙,且间隙周围存在3个静态节点,如图2所示,其中di,j表示节点si与节点sj之间的距离(如d1,2表示节点s1和s2之间的距离),则拓扑图G(V,E)中的V和E可以表示为V={s,s1,s2,s3,t},E={ds,1,ds,2,ds,3,…,d3,t}。
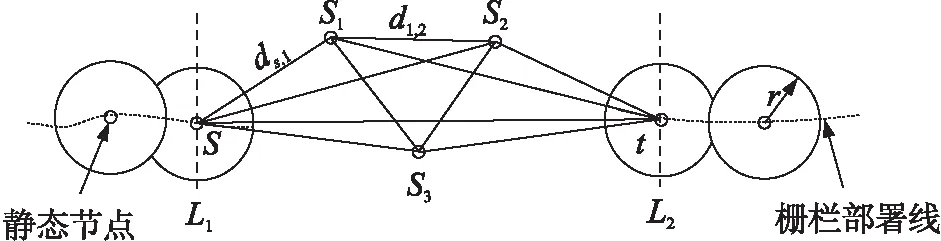
图2 静态节点全连接拓扑图
基于构建的静态节点全连接拓扑图,可计算出覆盖两节点之间的边所需的可移动节点数量。以图2中的节点s1和s2为例,覆盖节点s1和s2之间的边所需的最少可移动节点数量nm1,2可由式(2)计算得到。
nm1,2=「(d1,2-2r)/(2r)⎤
(2)
式中,d1,2表示节点s1与节点s2之间边的长度,r表示传感器感知半径。
根据式(2)得到的覆盖两节点之间的边所需的可移动节点数量,就可以将全连接拓扑图G(V,E),转化为所需的可移动节点数量需求拓扑图G′(V′,E′),其中V′代表分布在栅栏间隙周围的静态传感器节点,E′表示覆盖两节点之间的边所需的可移动节点数量。如图3所示,拓扑图中的元素可表示为V′={s,s1,s2,s3,t},E′={nms,1,nms,2,nms,3,…,nm3,t}。

图3 可移动节点数量需求拓扑图
1.3 KSP寻找最佳修复路径
在栅栏间隙修复时,可移动节点数量有限,因此应尽可能多的利用静态传感器节点,移动少量的可移动传感器节点完成栅栏的修复。当构建了从栅栏间隙起始节点s到终点t之间的可移动节点数量需求拓扑图之后,利用KSP算法寻找可移动节点数量需求拓扑图中的最佳路径,KSP算法可计算得到前K条最佳路径(前K条最短路径),这里的路径长度是指所需可移动节点的数量,最佳路径是指后续可能被修复的路径。如图4中,利用KSP算法寻找到2条最佳修复路径,其中修复路径P1最少需要3个可移动节点能够完成栅栏的修复(路径长度为3),修复路径P2需要4个可移动节点能够完成栅栏的修复(路径长度为4)。假设栅栏间隙处有3个可移动节点移动到修复路径P1的待修复位置V1、V2、V3即可完成栅栏的间隙修复,而如果存在4个或以上节点则能够完成P1和P2任意一条路径的修复。在K条最佳修复路径中,首先选择所需可移动节点数量最少的修复路径进行修复,因为多移动一个节点需要消耗大量的能量,不利于栅栏的长期生存。如果对最短路径进行修复时,可移动节点的移动距离总和大于次最短路径,则算法会选择次最短路径进行修复。
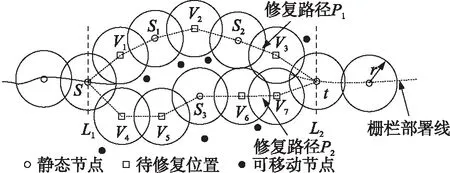
图4 KSP算法寻找G′的最佳修复路径图
1.4 匈牙利算法派遣可移动节点
找出拓扑图G′中的K条最佳修复路径之后,就可调度分布在栅栏周围的可移动节点进行栅栏修复。假设可移动节点的移动距离没有限制,可以通过派遣可移动节点对寻找到的最佳路径中的待修复位置进行栅栏修复。
首先判断可移动节点数量是否能够满足栅栏间隙的修复,如果可移动节点数量大于或等于待修复位置数量,则能够完成栅栏的修复,否则不能完成栅栏间隙修复。假如修复栅栏间隙需要m个可移动传感器节点,而有n个可移动节点可以被调度,且n>m,如何从n个可移动节点中选择m个节点对栅栏进行修复使得所有节点完成栅栏修复的移动距离总和最短是需要着重解决的问题。
如果修复路径中待修复位置的数量和可移动节点数量相同,则可以直接使用匈牙利算法完成节点的派遣工作,通过a个可移动节点去修复栅栏中a个待修复位置使移动节点的移动距离总和最小。当用于修复栅栏的可移动节点数量为n,而最短修复路径存在m个待修复位置,其中n>m,为了使匈牙利算法适用于可移动节点的派遣问题,需要虚拟出n-m个待修复位置,并且约定可移动节点到这些虚拟待修复位置的移动距离为0,如图5所示,可移动节点mi与待修复位置v4之间的移动距离为0。

图5 匈牙利算法指派可移动节点图
现假设待修复位置数为3,而可用于修复栅栏的可移动节点数为4,因此需要虚拟出1个待修复位置(图中v4为虚拟待修复位置),为寻找到的最短修复路径P1构造出匈牙利算法中的代价矩阵Mcost,如式(3)所示。
(3)
式中,di,j表示可移动节点mi与待修复位置vj之间的距离,以此类推,其中可移动节点到虚拟出的待修复位置的距离为0。
使用匈牙利算法对代价矩阵Mcost进行优化,得到一种代价最小的派遣方式,该派遣方式使修复栅栏间隙时可移动节点的移动距离总和最小,如图5所示,其中代价最小的派遣方式可表示为
Wmin={m1→v1,m2→v4,m3→v2,m4→v3}
即用移动节点m1去修复v1,m2修复v4,m3修复v2,m4修复v3,此时的移动距离总和dWmin可由式(4)计算得到。
dWi=da,1+db,2+dc,3+…+dn,n
(4)
式中,da,1表示移动节点ma到待修复位置v1的距离,同理db,2表示移动节点mb到待修复位置v2的距离,dn,n表示移动节点mn到待修复位置vn的距离。

图7 栅栏实验图
2 修复路径优化
由于栅栏间隙中的静态节点数量很多,在构建所需可移动节点数量拓扑图G′时,利用KSP算法寻找可移动节点需求拓扑图G′的最佳修复路径过程中很大概率上会出现多条最短修复路径和多条次短修复路径,如图6所示,存在3条修复路径,其中修复路径P1和P2为最短修复路径,需要3个可移动节点即可完成栅栏间隙修复,路径P3为次短修复路径,需要4个可移动节点才能完成栅栏的修复。由于可移动节点的分布不同,造成可移动节点移动到这2条最短修复路径P1和P2上的待修复位置的移动距离并不相同,因此当多条最短修复路径存在时,利用匈牙利算法分别计算可移动节点修复每条最短路径的移动距离总和,然后选择距离总和最短的修复路径完成栅栏的修复。

图6 修复路径优化图
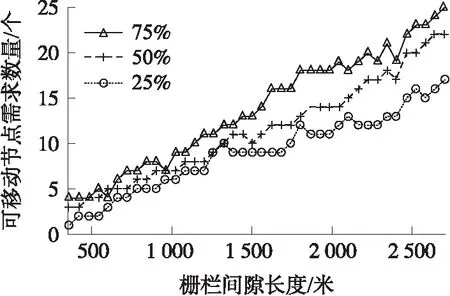
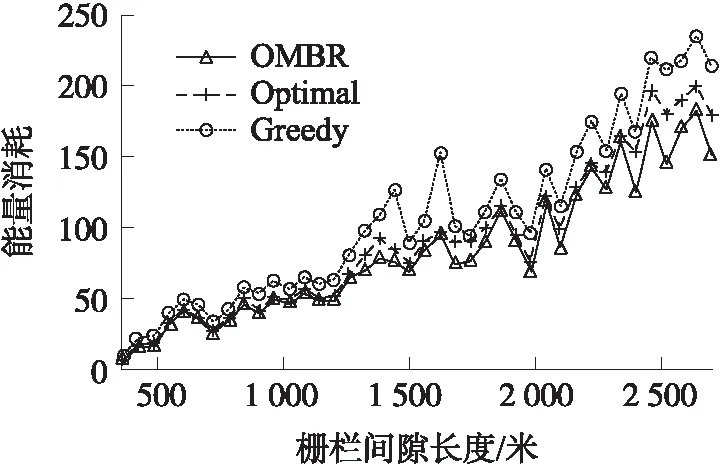
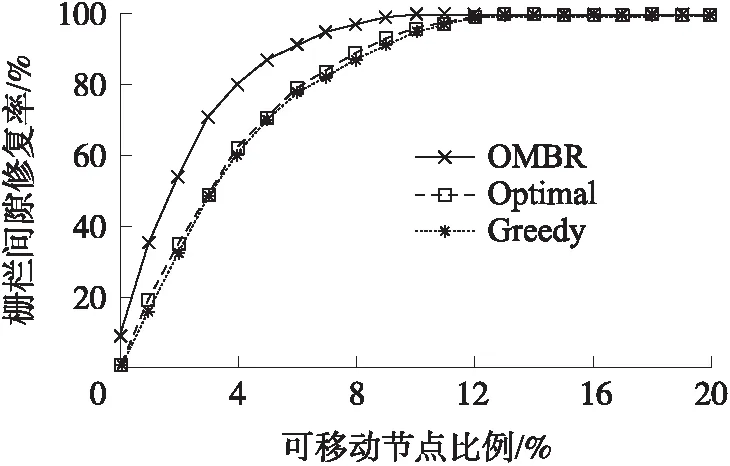
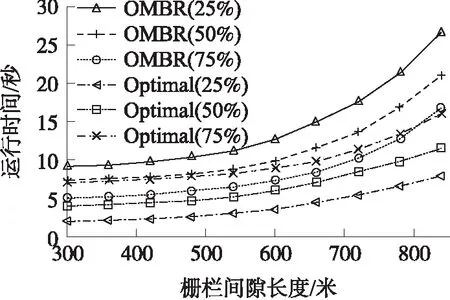
然而并不一定修复最短路径是可移动节点的移动距离总和最短的,也可能是修复次最短路径时移动距离总和最短。因此利用KSP算法求得K条最佳修复路径,K条最佳修复路径中包含了最短修复路径和次最短修复路径。假如部署区域内可移动节点的数量足够(能够满足最短路径和次最短路径的修复),修复次最短路径P3需要4个可移动传感器节点,可移动节点的移动距离总和为D1,修复最短路径P1需要3个传感器节点,可移动节点移动距离为D2,而D1 实验的硬件环境为i7处理器、8G内存的PC机,采用MATLAB R2013a仿真软件进行编程。将传感器节点部署在一个长为3 000 m,宽为200 m的矩形区域中,在该区域中随机部署100个传感器节点(包括静态传感器节点和可移动传感器节点),传感器节点的感知半径r为45 m。在监测区域内已经通过参考文献[21]提出的栅栏构建方法构建了一条栅栏,由于某些因素导致栅栏出现间隙,需要进行修复,如图7所示,图中栅栏中间出现了间隙,采用本文提出的修复方法进行栅栏修复。 修复不同长度的栅栏间隙所需要的可移动节点数量是不同的,理论上间隙越长,则需要可移动节点数量越多。仿真实验验证栅栏间隙长度与可移动节点数量之间的关系,图8验证了可移动节点比例分别为75%、50%、25%情况下修复不同长度的栅栏间隙所需要的可移动节点数量,实验数据为100次独立重复实验的平均结果。从图8可知,随着栅栏间隙长度的增加,修复栅栏需要的可移动节点数量逐渐增加,且呈线性增长。可移动节点比例越高,则修复栅栏间隙需要的可移动节点数量越多。因为可移动节点在总部署节点中的占比越高,则静态节点的比例越低。OMBR栅栏修复方法是尽可能地使用静态节点构建修复路径,因此当栅栏间隙长度不变的情况下,静态节点的数量越少,则需要可移动节点数量就越多。 图8 可移动节点需求数量图 栅栏修复过程中可移动节点的平均移动距离是评价栅栏修复方法的重要指标,平均移动距离越短,则修复栅栏花费的代价越少,即消耗的能量越少,越有利于栅栏的长期生存。为验证栅栏间隙长度对可移动节点的平均移动距离的影响,实验中可移动节点占总部署节点的比例为50%,结果如图9所示。实验对比了参考文献[23]提出的最佳修复方法和广泛用于栅栏间隙修复的贪婪算法,分别记为Optimal和Greedy,其中最佳修复方法性能卓越,是目前比较优秀的一种栅栏间隙修复方法。 图9 平均移动距离图 从图9可以看出,随着栅栏间隙长度的增加,可移动节点的平均移动距离逐渐增加,但增加速度缓慢。在利用贪婪算法修复栅栏间隙时,可移动节点的平均移动距离最长,OMBR栅栏修复方法修复间隙时可移动节点的平均移动距离最短,最佳修复方法修复栅栏间隙时可移动节点的平均移动距离略高于OMBR。OMBR算法从间隙修复的全局考虑,使得所有可移动节点的移动距离最短,贪婪算法选择最接近待修复位置的移动节点修复栅栏,会陷入局部最优问题,最佳修复方法采用二分查找法计算节点的移动距离,虽然效率较高,但是不能完全达到最优,存在误差。 在利用可移动节点修复栅栏间隙的过程中,节点的能量消耗与节点移动的距离呈正相关,由于节点移动所消耗的能量远远高于其他行为消耗的能量,因此在栅栏修复过程中忽略其他能量消耗。假设节点移动10 m,消耗一个单位的能量,实验中可移动节点占总部署节点数量的50%,实验对比了贪婪算法和最佳修复方法,可移动节点修复栅栏间隙所消耗的能量,如图10所示。 图10 能量消耗分析图 实验结果表明在修复相同的栅栏间隙时,OMBR算法消耗的能量最少,其次是最佳修复方法,能量消耗最多的是贪婪算法。根据图9的实验结果,OMBR算法修复栅栏间隙的平均移动距离最短,其次是最佳修复方法,贪婪算法的平均移动距离最长,而可移动节点修复间隙的能量消耗与移动距离呈正相关。因此,实验验证了OMBR算法在栅栏修复方面的总体性能比其他两种算法更好。 为验证部署区域内可移动节点的比例与栅栏间隙修复率的关系,实验对比了最佳修复方法和贪婪算法,实验中栅栏间隙的长度为1 000 m,结果如图11 所示。 图11 栅栏间隙修复率图 从图11可以看出,当没有可移动节点时,OMBR的修复率达到了9%,而最佳修复方法和贪婪算法修复率为0%,主要是因为OMBR算法充分利用了分布在栅栏间隙处的静态节点进行栅栏的初期修复,在只有静态节点的情况下栅栏能被部分修复,而最佳修复方法和贪婪算法仅利用可移动节点进行间隙修复,所以当没有可移动节点时修复率为0%。总体上,OMBR栅栏间隙修复率比最佳修复方法、贪婪算法的修复率都高,其中最佳修复方法与贪婪算法的修复率相当,因为在可移动节点的移动距离不限的情况下,部署区域内的移动节点可以移动到栅栏间隙的任意待修复位置,所以最佳修复方法与贪婪算法的修复率基本接近。 算法复杂度也是衡量栅栏间隙修复方法好坏的重要指标之一。图12分别验证了OMBR算法和最佳修复方法在不同比例的可移动节点情况下完成栅栏修复所运行的时间。 图12 算法运行时间图 由图12可知,OMBR算法随着可移动节点比例的增加,修复栅栏消耗的时间逐渐降低。由于OMBR算法采用静态节点构建拓扑图,因此构建的拓扑图规模比较小,算法所消耗的时间较短。最佳修复方法随着可移动节点的比例增加,修复栅栏消耗的时间逐渐增加,因为该方法采用可移动节点构建拓扑图,然后计算拓扑图的最大流完成栅栏的修复,因此随着可移动节点数量的增加,算法修复栅栏间隙所花的时间也会增加。随着栅栏间隙长度的增加,这两种算法消耗的时间都呈指数增长,因为栅栏间隙长度增加,这两种算法在修复栅栏间隙时构建的拓扑图规模也呈指数增长。 将OMBR修复法与最佳修复方法进行对比,当移动节点所占比例为25%、50%时OMBR算法比最佳修复方法的时间复杂度高。但在可移动节点比例为75%,栅栏间隙小于800 m的情况下,OMBR算法的时间复杂度比最佳修复方法低。因为OMBR算法采用静态节点建立拓扑图,当栅栏间隙短,可移动节点的所占比例比较高时,OMBR算法构建的静态节点拓扑图规模较小,最佳修复方法构建的拓扑图规模较大,因此OMBR算法的运算时间比最佳修复方法小。综上所述,虽然OMBR算法时间复杂度在一定程度上比最佳修复方法略高,但在栅栏间隙小,移动节点比例高的情况下,OMBR的时间复杂度比最佳修复方法低。 针对可移动节点进行WSN栅栏间隙修复问题,提出一种WSN栅栏间隙修复优化方法,利用分布在栅栏间隙周围的静态节点,使可移动节点的移动距离总和最小。仿真实验表明该方法在降低网络能耗、提高栅栏间隙修复率方面具有较好的性能,但仍然存在不足之处,如传感器节点数量较大时,算法的复杂度略高。在后续的工作中,降低OMBR算法复杂度,并将无线传感器节点部署于实际场景的带状区域以对穿越区域的移动物体进行监测,当部署的栅栏出现间隙时,利用本文提出的栅栏间隙修复方法进行修复,对方法在实际场景下的应用中进一步验证。3 仿真实验
3.1 可移动节点需求数量
3.2 平均移动距离

3.3 栅栏修复过程能耗分析
3.4 栅栏间隙修复率
3.5 算法复杂度
4 总结
