基于改进拟牛顿-K近邻的TDOA定位算法

徐耀松,谭 亮

(辽宁工程技术大学电气与控制工程学院,辽宁 葫芦岛 125105)

TDOA(Time Difference Of Arrival)方法在室内声源定位是进行声源定位的一种有效的方法[1]。主要分为两个步骤:首先麦克风阵列获取声音信号到达麦克风阵列之间的时间差,获得时间延迟;然后基于时间延迟求解非线性定位方程,求出声源位置。对于非线性定位方程的求解方法主要分为两类[2]:第1类为目标函数搜索的定位算法,这种方法需要对定位空间搜索遍历,运算量大,常用的方法有最大似然估计法[3]、球型插值法[4];第2类方法根据传感器的布设情况,直接解非线性方程得到所要求的坐标。解非线性方程常见的无约束一维极值的方法主要包括:黄金分隔法[5],进退法[6],牛顿法[7]等等;无约束多维极值的方法主要包括:模式搜索法[8],最速下降法[9],拟牛顿法[10]等等。因定位方程维度较高,所以在解定位方程时更加适用于使用无约束多维极值的方法。模式搜索法不用计算目标函数导数,只需要计算函数值,但其不适用于目标函数复杂的情况下。最速下降法又称为梯度下降法,易于编程,但其收敛速度并不快,在高维的优化问题和精度要求较高的情况下,缺点更为明显。一般情况下,该方法一般与其他算法配合使用。而拟牛顿方法在维度较高情况下可以较准确的得出非线性方程解,计算效率较高。因此选择拟牛顿方法解定位方程。然而拟牛顿方法计算速度较慢,在时延估计存在噪声的情况下,拟牛顿定位的准确度也有所下降,本文提出一种改进拟牛顿-K均值定位方法对声源进行定位。提出一种近似矩阵替换雅可比矩阵,提高非线性定位方程拟牛顿算法求解的速度,根据噪声性质改变K近邻算法的距离,提高系统定位结果的准确性。

1 拟牛顿方法及其改进

定位估计系统可以看成解决非线性等式问题:

F(α)=0,α∈Rn

(1)

式中,α为声源坐标向量,若为三维空间定位,α则为三维坐标。

传统的拟牛顿的方法的迭代公式为:

Jk(αk+1-αk)=F(αk)

(2)

式中,Jk是非线性定位方程F(αk)的雅可比矩阵。利用定位估计非线性方程F与其一阶导数g包含的信息,得到目标函数的曲率近似,具有易实现的特点。但是当计算维数较高时,求解雅可比矩阵的花销就变大,为解决雅可比阵运算花销大的问题,利用下式替换拟牛顿算法的雅可比矩阵[11]

(3)

式中,Uk为雅可比矩阵的近似阵,vk=αk+1-αk,fk=F(αk+1)-F(αk),利用近似矩阵Uk代替雅可比矩阵Jk。如式(4)和式(5)所示:

Uk(αk+1-αk)=F(αk)

(4)

Uk+1(αk+1-αi)=F(αk+1)-F(αi),i∈[0,k]

(5)

令vk=αk+1-αk,Jk=J(αk),得到新的拟牛顿等式:

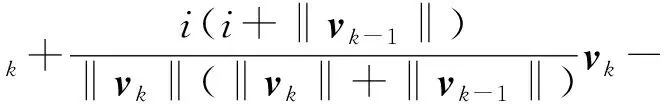
(6)

将式(6)代入式(2),求导:

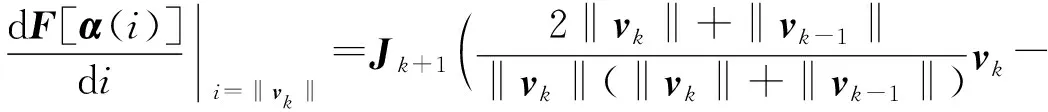
(7)

由于时延估计结果的定位方程为二次的,可以用如下二次方程R(i)逼近定位系统:

R(i)=ai2+bi+c

(8)

式中,a,b,c为各项系数。为逼近时延估计的定位方程,式(8)需要满足以下条件:

R(0)=F[α(0)]=F(αk)=Fk

R(‖vk‖)=F[α(‖vk‖)]=F(vk+1)=Fk+1

R(-‖vk-1‖)=F[α(-‖vk-1‖)]=F(vk-1)=Fk-1

则可得到:

(9)

(10)

c=Fk

(11)

同样地,将式(9)～式(11)代入式(8)并求导得到:

(12)

令式(12)和式(7)相等,并令fk=Fk+1-Fk得出:

(13)

简化上式,令:

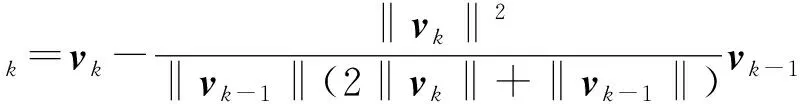
(14)

(15)

从而:

Jk+1χk=γk

(16)

如果用Uk逼近Jk,则:

Uk+1χk=γk

(17)

最后,由式(3),(14)和(15)得到的更新Uk的公式如下:

(18)

由于式(18)中的近似矩阵Uk与αk-1、αk、αk+1三项的取值有关,因此在解方程时,首次迭代使用构造雅可比矩阵的拟牛顿方法;第2次迭代使用BBM方法;之后便可利用式(18)的近似矩阵更新迭代公式,直至满足停止条件,迭代结束。具体运算步骤为:①设置迭代起始点α0,求取雅可比矩阵J0,令U0=J0。②通过U0v0=-F(α0),求取v0进而求取α1,f0。③通过式(3)求得U1,使用U1v1=-F(α1)求取v1,α2,f1。④通过式(14)、式(15)求得χ1,γ1。⑤通过式(18)求得Uk,并通过Ukvk=-F(αk)求取vk,αk,fk。观察αk是否满足停止条件。满足则结束迭代;不满足则k=k+1并返回步骤④。

2 基于改进K近邻算法的定位估计

在室内声源定位过程中时延估计结果容易受到环境噪声的影响,在观测次数有限的情况下,尤其是实时性要求较高的场合,采用改进拟牛顿定位方法会产生较大的误差。为了提高定位的准确性,降低时延估计噪声对结果的影响,提高算法的鲁棒性,提出采用改进的K近邻方法进行定位结果的最优估计。

2.1 K近邻学习方法

K近邻学习算法根据提供测试的样本,通过比较待测样本和提供样本之间的距离度量,选择最靠近的K个样本点,使用这K个样本点对结果进行估计[12]。

例如对同一个点估计20次,把20次定位的平均值作为学习样本输入,将20次估计点作为待学习的样本。通过计算学习样本和待学习样本之间的距离,一般采用欧式距离:

(19)

式中,x*是学习例子,xi是待学习例子,将计算的结果进行排序,选择距离最近的K个值,达到抑制噪声的目的。

2.2 K近邻的改进方法

实际中由于提供的估计点数有限,使用传统的均值方法选择学习样本的效果并不理想,K近邻算法中单纯基于欧式距离的求解精确程度不高。本文提出采用密集距离法估计定位点,即计算有限含噪估计点的相互距离,而非估计点到均值点的距离,如下

rij=|xixj|

(20)

式中,i,j=1,2,…,n且i≠j。通过距离rij,寻找距离之和最短且成群的点集,将均值点作为学习样本,使用K近邻算法选出K个点,采用打分方法选择合适的权值。

该方法实施时,可根据最大距离与估计点比值设置多个距离阈值∂1,∂2,…,∂t,在阈值内的距离值可以获得相应的分值βi,i∈t,距离越近分值越高;多个点距离在最小距离阈值内且聚集在一起也会得到分数的加成βt(n-1),i∈t,n是聚集点数。

然后,根据下式求出声源位置:

(21)

综上所述,基于IQN-IKN方法的TDOA定位过程可概括如下:①通过麦克风阵列得到时延估计结果,得到定位方程。②通过改进的拟牛顿方法求出方程组的解。③采用改进K近邻的方法对估计误差进行抑制,优化定位的准确度。

3 实验分析

3.1 二维空间定位实验

为验证方法的快速和准确性,分别采用改进拟牛顿方法和传统拟牛顿方法在二维空间进行比较。定位区域是150 cm×150 cm的平面,麦克风传感器设置在一角并建立笛卡尔坐标系,设置在坐标(0,10),(10,0),(-10,0)和(0,-10)的位置(单位:cm),如图1所示。

图1 实验布局图

将声源(频率为100 Hz～5 000 Hz,主要为语音信号)设定在第一象限中,设定固定的迭代起始点(2,2)(单位:cm),停止条件为误差0.000 1(单位:cm)。随机放置声源,分别采用拟牛顿算法和改进拟牛顿算法进行多次声源定位对结果求取平均值,测试结果如表1所示。

表1 不同声源的迭代计算结果

表1结果表明改进拟牛顿算法相对于传统拟牛顿算法进行声源定位的速度更快。以声源位置为(8,10)(单位:cm)为例,比较两种算法每一次迭代的误差和时间。如图2所示。

图2 定位结果误差对比

可见改进拟牛顿的算法相对于拟牛顿每次迭代的速度更快,同一迭代周期内的误差更小。

3.2 三维空间定位实验

实验场所设置为长5 m,宽3 m,高2 m的三维空间,同样建立三维笛卡尔坐标系。将声音传感器设置在x,y,z轴的距离原点10cm的位置。如图3所示。

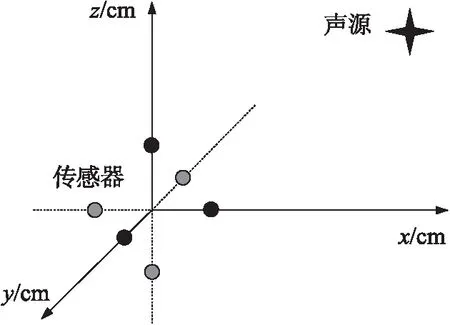
图3 室内布局图

图4 含噪定位点与定位点

选择迭代的起始点是(50,50,50)(单位:cm),设置迭代停止条件为最小均方差为1cm,随机选择空间点进行多次定位并计算均值。记录拟牛顿方法和改进拟牛顿方法的迭代次数和运算时间。

三维空间定位实验结果证明,改进拟牛顿比传统拟牛顿方法在三维空间定位的速度明显更快。相对于二维空间定位实验结果,定位的维度越高,采用改进拟牛顿算法比传统拟牛顿的收敛速度更快。

表2 不同声源位置的迭代计算结果

3.4 含噪声情况的声源定位估计

为了验证含噪声情况下改进拟牛顿方法的声源定位效果,对二维空间点(75,75)(单位:cm)定位并在时延估计结果中分别加入信噪比为0 dB,10 dB,20 dB,30 dB的高斯白噪声,采用拟牛顿方法的定位结果如图4所示。

可见,在噪声影响下改进拟牛顿方法的定位结果产生误差,甚至会产生偏离较大的异常定位结果,针对这一问题,采用本文提出的改进K近邻方法优化定位估计结果。

为验证本文方法的性能,分别使用均值、K近邻和改进K近邻方法进行定位求解。

选择10组估计点并对每一组数据分别加入信噪比0 dB、10 dB、20 dB和30 dB噪声后进行估计20次,分别用均值方法、K均值方法以及改进K均值方法估计定位点。得出定位结果均值如表3～表6 所示。

从表3～表6可以看出改进K近邻方法能够获得更准确的二维空间定位估计。

选择一处高3.5 m,长6 m,宽4 m的空间。在室内的角落搭建实验设备。选择的声源是一个5 V的有源蜂鸣器,其频率在语音频率内为(2 300±500)Hz。随机选择位置进行定位估计。实验结果如表7所示。

表3 二维空间信噪比为0 dB定位结果

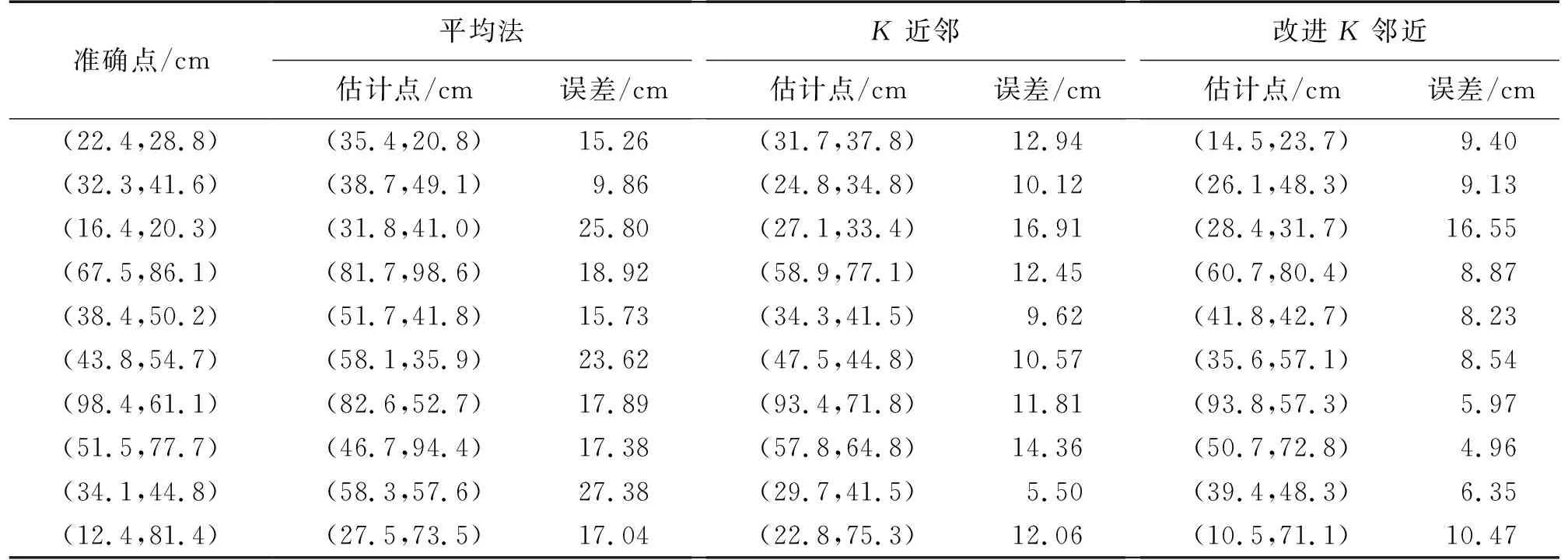
表4 二维空间信噪比为10 dB定位结果

表5 二维空间信噪比为20 dB定位结果

表6 二维空间信噪比为30 dB定位结果

表7 三维空间含噪声定位结果

从表7可以看出,改进K近邻方法具有很好的鲁棒性,并且定位误差小。改进K近邻算法优化室内定位效果明显。

4 结论

对于TDOA声源定位系统定位估计阶段,定位方程求解速度和环境噪声是影响定位系统主要问题。本文提出IQN-IKN算法,构造二次方程逼近定位估计的定位方程,得到近似雅可比矩阵并用其代替传统拟牛顿中的雅可比矩阵,减少了系统定位的时间,提高定位求解速度;在含噪声环境下,采用基于密集距离和打分策略的改进K近邻方法估计定位点,在不减少定位时间的前提下,同样能够提高定位方法的准确性和鲁棒性。本方法可以用于室内和信噪比较大的户外声源定位场合。