水-土-结构耦合作用下地铁区间隧道抗震仿真分析
2018-11-02商金华王晓昱毛荣吉
商金华 王晓昱 毛荣吉
(济南轨道交通集团有限公司,250101,济南//第一作者,高级工程师)
济南市作为山东省省会,由于泉水保护等原因,城市轨道交通建设起步较晚,且随着近年来交通拥堵的恶化,大力发展城市轨道交通建设势在必行。
地下结构由于受到周围岩体或土体的约束,一直被认为具有良好的抗震性能[1-3]。但近年来的地震中许多原本被认为具有良好抗震性能的地下结构(包括区间隧道及地铁车站等)都发生了不同程度的破坏,引起了许多学者的重视。在区间隧道的抗震设计研究中,数值方法已成为重要的研究途径,近年来取得了丰硕的成果。文献[4]运用有限元和无限元耦合的分析方法对土-地下隧道的相互作用进行了分析。文献[5]结合动力有限元-双渐近多向透射边界编制了相应的计算程序,来计算软土地层中盾构隧道的地震响应。文献[6]以南京某软弱地基浅埋地铁区间隧洞为研究对象,进行地震响应分析。文献[7]利用土-结构相互作用的动力有限元方法,通过引入无长度的三自由度弹簧单元模拟纵向螺栓接头,分析行波波长、地基刚度与阻尼对盾构隧道纵向地震响应的影响。文献[8]运用有限元软件ANSYS对某隧道建立二维有限元模型,采用一致边界条件进行地震响应分析。
虽然对区间隧道的抗震设计研究较多,但是针对济南市地下泉水众多的独特地形,对于水-土-结构耦合作用下地铁区间隧道抗震分析的研究还较少。因此,本文在常规地铁抗震分析的基础上考虑水-土-结构的耦合作用,研究地震作用下区间隧道的反应,以及地下水渗流对地铁区间隧道抗震性能的影响,从而为济南市地铁区间隧道的抗震设计提供参考。
1 水-土-结构耦合作用抗震模型
1.1 结构概况
以济南轨道交通R1线大杨庄站—济南西站双洞区间隧道为研究背景。区间隧道采用盾构法施工,隧道内径5.8 m,外径6.4 m,采用平板型管片,管片采用C50混凝土、厚度30 cm,沿隧道纵向管片宽度1.2 m,隧道顶板埋深10~20 m,两洞之间的间距为14 m。盾构隧道纵坡为V形,形成高站位低区间的型式。
1.2 工程地质与水文地质
根据济南市轨道交通R1线大杨庄站—济南西站岩土工程勘察报告(详勘阶段),选取具有代表性的济南土层作为地铁区间隧道所处的场地,从上至下依次为:黄土、粉质黏土、细砂、粉质黏土、卵石、黏土。
大杨庄站—济南西站地下水的存在形式主要为第四系松散孔隙水,其埋藏类型为潜水和承压水。其中潜水水位埋深5.0~8.0 m,承压水水位埋深6.3~8.2 m。
1.3 计算模型
1.3.1 模型建立
运用FLAC3D5.0软件分别建立考虑和不考虑地下水渗流作用的区间隧道三维计算模型,为了减少边界效应对计算结果的影响,取自隧道轴线起向两侧各延伸4D(D为隧道直径),总宽度为62 m;竖向和纵向计算深度均取为60 m;隧道埋深为20 m。
1.3.2 边界条件
模型四周及底面施加法向约束,上部为自由边界。动力计算时模型周围采用自由场边界。考虑地下水渗流时,在此基础上模型四周及底面采用不透水边界,上部采用透水边界。为考虑地下水渗流的作用,同时加快水-土-结构耦合作用的计算速度,在模型上部加上水头高度为5.5 m的静水头。
1.3.3 材料模型
土层采用实体单元模拟,各地层视为各向同性Mohr Coulomb理想弹塑性材料,管片采用壳单元模拟,土体阻尼取为滞后阻尼。主要土层的动静力及水力计算参数如表1所示。管片材料的动静力计算参数如表2所示。地铁区间三维模型如图1和图2。

表1 典型场地土动静力及水力计算参数表

表2 管片材料动静力计算参数表

图1 土-地铁区间隧道有限元模型
1.4 地震波
济南轨道交通地铁区间隧道的抗震设防烈度为7度,同时参考山东省地震工程研究院提供的《济南市轨道交通R1线一期工程场地地震安全性评价报告》中提供的50年超越概率2%的基岩地震波,本文选取具体地震波如图3所示。

图2 隧道有限元模型
1.5 监测点的布置
为了更好地分析地震作用下隧道区间的位移和内力响应,在隧道左、右线均布置了8个监测点,布置如图4所示。
2 水-土-结构耦合作用时地铁区间隧道的位移响应
沿x方向(垂直于隧道方向)在模型底部输入基岩地震波,分别计算考虑地下水渗流和不考虑地下水渗流作用时地铁区间隧道在罕遇地震作用下的位移。将监测点1、2、3、4的位移极值汇总于表3,并分别给出两个模型洞顶(监测点1)和洞底(监测点2)两点的位移时程图,如图5和图6所示。

图3 基岩地震波

a) 左线
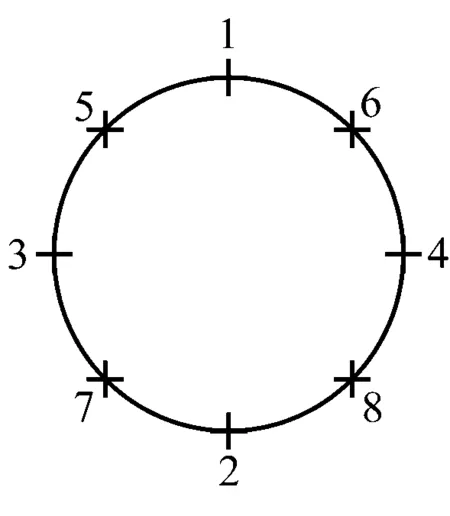
b) 右线图4 区间隧道监测点布置图

表3 考虑和不考虑地下水渗流时隧道监测点地震位移极值

图5 考虑和不考虑地下水渗流时监测点1位移时程曲线
由表3和图5、6可知,罕遇地震作用下,考虑地下水渗流时,隧道左线洞顶位移极值35.88 mm,洞底位移极值34.79 mm,左洞腰位移极值35.35 mm,右洞腰位移极值35.37 mm。各监测点的位移时程曲线相似,大约在14 s左右位移正向达到极值,18 s左右位移负向达到极值,且位移极值随着埋深位置的增大而减小,洞顶处位移最大,洞腰处位移次之,洞底处位移最小。

图6 考虑和不考虑地下水渗流时监测点2位移时程曲线
此外,考虑地下水渗流时区间隧道的位移反应规律与不考虑地下水渗流作用时一致,但由于渗流力的作用使得土体有效应力增大,各监测点位移极值增大。
除了各监测点位移值,一般需要计算出隧道洞顶和洞底之间的相对位移,从而利用相对位移和隧道外径的比值求得隧道的倾斜角度,以评价隧道横向的安全性。根据《盾构隧道的抗震研究及算例》的规定,当倾斜角小于1/350时,结构的安全性没有问题。
考虑地下水渗流和不考虑地下水渗流作用时,区间隧道洞顶和洞底的相对位移时程图如图7所示,隧道计算倾斜角如表4所示。

图7 考虑和不考虑地下水渗流时洞顶和洞底的相对位移时程曲线
考虑地下水渗流时,区间隧道洞顶和洞底相对位移增大,这是由于在地震力基础上,考虑了渗流力的作用,且洞顶的渗流力要大于洞底的渗流力,使得相对位移增大。由表4可知,相对位移极值为2.03 mm,倾斜角最大为1/2 955,仍能满足规范要求。
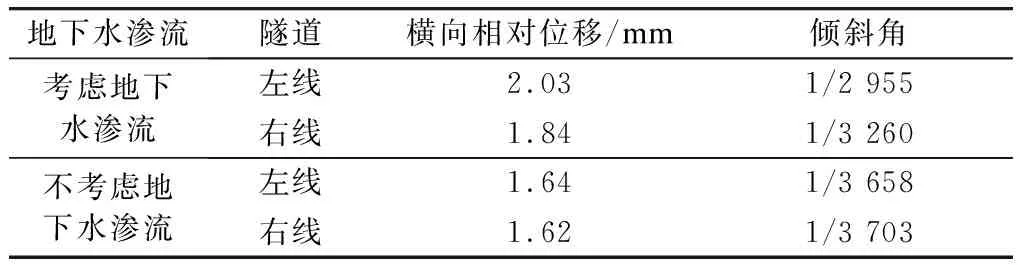
表4 考虑和不考虑地下水渗流时隧道倾斜角
3 水-土-结构耦合作用时地铁区间隧道的内力响应
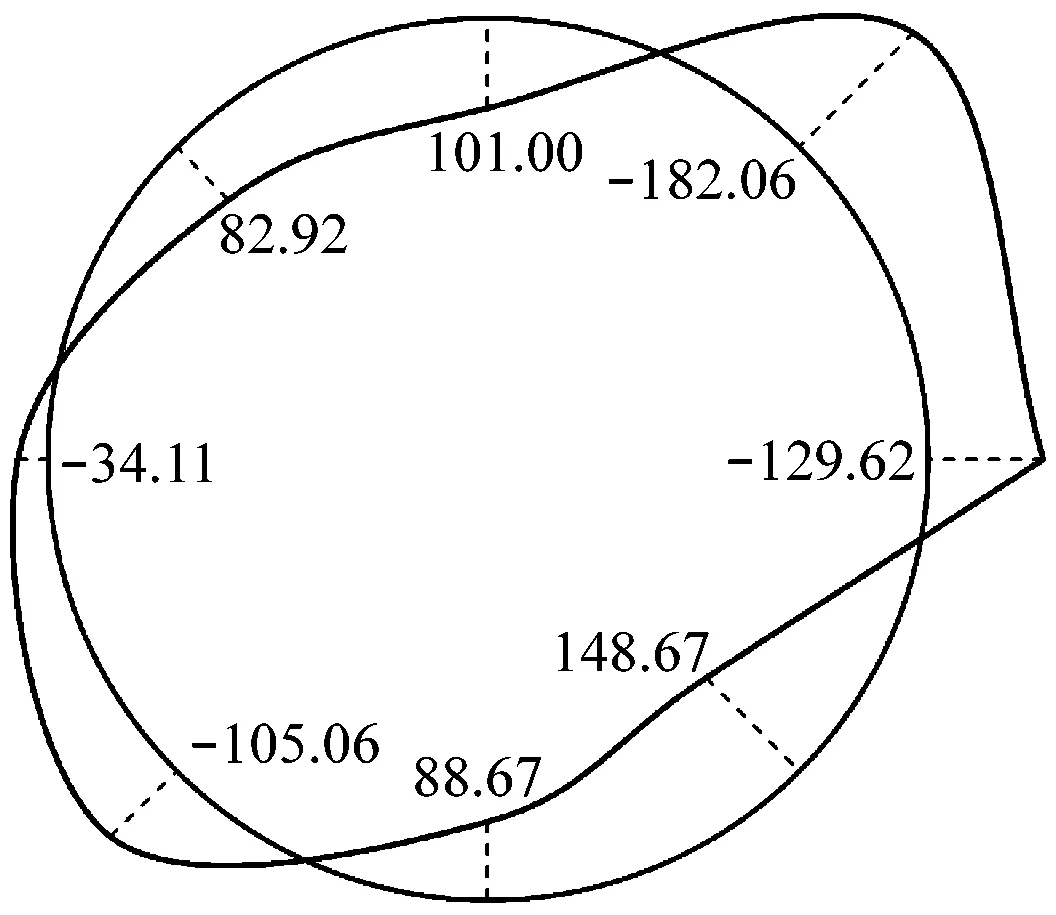
分别提取考虑地下水渗流和不考虑地下水渗流作用时地铁区间隧道在罕遇地震作用下各监测点的弯矩、剪力和轴力极值汇总于表5和表6中。并绘制考虑地下水渗流作用时地铁区间左右线内力反应包络图如图8所示。

表5 考虑地下水渗流时各监测点内力极值

表6 不考虑地下水渗流时各监测点内力极值
由表5和图8可知,考虑水-土-结构耦合作用时,区间隧道轴力最大值一般发生在洞腰处,且里侧洞腰的轴力值较大,整个结构处于受压状态;剪力的最大值一般发生在靠近中间位置处与洞顶和洞底成45°的2个点附近;弯矩的最大值与轴力相同,出现在拱腰处,且里侧的拱腰的弯矩值较大。考虑水-土-结构耦合作用时,地震作用下内力规律与不考虑地下水渗流时一致。
此外,相比于不考虑地下水渗流作用,考虑地下水渗流时,区间隧道所受弯矩、剪力减小,轴力增大。区间隧道最大弯矩减小了70.58 kN·m,最大剪力减小了120.10 kN,最大轴力增大了448.645 kN。因此考虑地下水渗流作用时轴力增大较多,存在一定的安全隐患。
4 结论
本文依托于济南轨道交通R1线大杨庄站—济南西站双洞区间隧道,分别建立考虑土-结构相互作用模型和水-土-结构耦合作用模型,研究水-土-结构耦合作用下区间隧道的地震反应,以及地下水渗流对地铁区间隧道抗震性能的影响,主要得出以下结论:
(1)位移极值随着埋深位置的增大而减小,洞顶处位移最大,洞腰位移次之,洞底处位移最小。洞顶和洞底的相对位移、倾斜角满足规范要求。
(2)轴力的最大值一般发生在洞腰处,内侧洞腰的轴力值较大,整个结构处于受压状态;剪力的最大值一般发生在靠近中间位置处与洞顶和洞底成45°的2个点附近;弯矩的最大值与轴力相同,出现在洞腰处,且里侧洞腰的弯矩值较大。

左线
左线

左线

右线a)弯矩反应包络图(单位:kN·m)

右线b)剪力反应包络图(单位:kN)
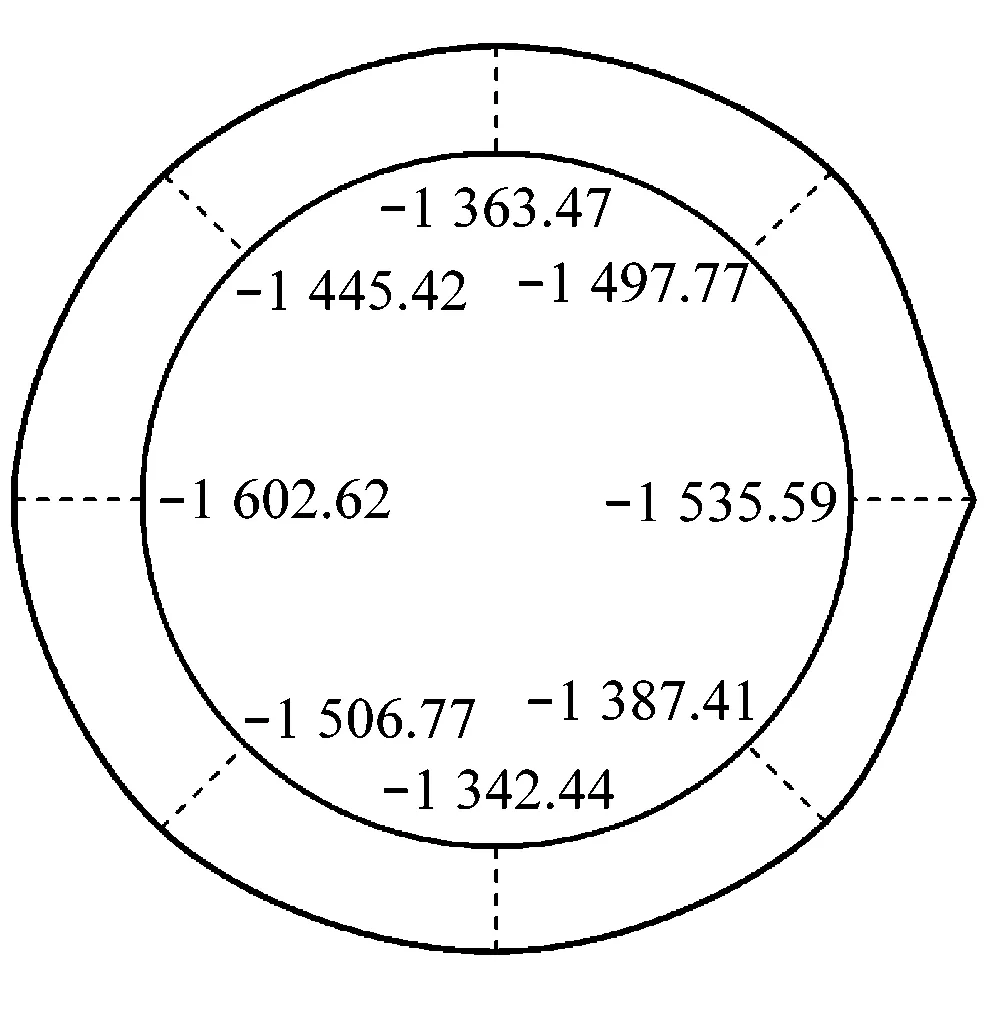
右线c)轴力反应包络图(单位:kN)图8 水-土-结构耦合作用时地铁区间隧道的内力反应包络图
(3)与不考虑地下水渗流作用时区间隧道的计算结果相比,考虑地下水渗流时,区间隧道的位移和内力地震响应规律相同,但隧道位移值增大,洞顶和洞底的相对位移值也增大;区间隧道各监测点的弯矩、剪力值有所减小,轴力有所增大。
