From flatness,GPI observers,GPI control and flat filters to observer-based ADRC

Hebertt SIRA-RAM´IREZ

CINVESTAV-IPN,Department of Electrical Engineering,Mechatronics Section,Avenida IPN No.2508,Col.San Pedro Zacatenco CP 07360,CDMX,M´exico

Received 30 June 2018;revised 10 August 2018;accepted 10 August 2018

Abstract

In this article,we establish the route taken by the author,and his research group,to bring differential flatness to the realm of active disturbance rejection control(ADRC).This avenue entitled:1)generalized proportional integral observers(GPIO),as natural state and disturbance observers for flat systems,2)generalized proportional integral(GPI)control,provided with extra integrations,to produce a modular controller known as flat filters(FF’s)and,finally,3)the establishing of an equivalence of observer based ADRC with FF’s.The context is that of pure integration systems.The obtained controllers depend only on the order of the flat system and they are to be directly used on the basis of the available flat output signal in a universal,modular,fashion.The map is complemented with the relevant references where the intermediate techniques were illustrated and developed,over the years,in connection with laboratory experimental implementations.

Keywords:Flatness,GPI observers,GPI control,reduced order GPI observers,flat filters

1 Introduction

Differential flatness is a system property establishing,in a natural manner,an input output description of the system,thus easing the controller design task in,both,SISO(single-input single-output)and MIMO(multiple inputs multiple outputs)nonlinear systems within a zero dynamics-free environment.All system states and the control inputs are differentially parameterizable in terms of the flat outputs and of a finite number of their time derivatives with a clear opportunity for identification of possible structural singularities.The flatness property substantially eases off-line trajectory planning issues,while trivializing feedback controller design.One of the advantages of the flatness property,in their inputto-flat-output representation of the dynamics,is that it allows to efficiently circumvent matching conditions,as it naturally leads to trivially matched input-to-flatoutput models.Flatness allows for exact static feedback linearization,for SISO systems,and to clearly identify the need for static or dynamic feedback linearization,in MIMO nonlinear systems.Flatness easily leads to controller synthesis based on desirable input to flat outputs closed-loop dynamics,in total absence of unobservable zero dynamics.In the linear system case,flatness is completely equivalent to system’s controllability,while flat outputs are trivially observable.

Nonlinear differentially flat systems are equivalent to perturbed chains of pure integration.Treating,via drastic model simplification,the effects of endogenous nonlinearities in combination with exogenous inputs into a single footing of total unknown,unstructured,disturbance(addressed as thetotal disturbance),immediately prompts for the need of,simultaneous,state and disturbance estimates.Generalized proportional integral(GPI)observers are extended state observers traditionally used for robust phase variable reconstruction and high-gain based disturbance estimation,including the estimation of a finite number of disturbance input time derivatives.Integral phase variables reconstruction,via iterated inputs and outputs integrations,with suitably added iterated output integral compensation is an alternative to GPI observer design,which is known as GPI control.The GPI control scheme establishes a means of circumventing nonlinear observers design in both SISO and MIMO nonlinear systems.The key point here is to carry out the GPI observer,or GPI controller design,for the unperturbed version of the system,and,then,assess the effect of the neglected disturbance on the closed-loop response of the system to the designed controller.The scheme results in attenuation or disturbance rejection properties and generates a desirable,robust,trajectory tracking,or output stabilization,performance.

The robustness consideration of GPI controller design,on flat systems simplified to perturbed chains of pure integrations,directly results in a high gain FF with desirable trajectory tracking qualities simultaneously achieved with low frequency input disturbance rejection and high frequency output measurement noise filtering or attenuation.

In this article,we establish the route,taken by the author and his colleagues,students and coworkers,to bring Differential Flatness to the realm of ADRC design.This entitled GPI observers,GPI control via integral reconstructors and,finally,the establishing of an important equivalence between Observer based ADRC and robust linear control based on FF’s.This developments clarified,step by step,the way to establish a complete equivalence of ADRC via reduced order extended observers,and robust GPI control based on integral reconstructors also called FF’s.The context,quite on purpose,is that of pure integration systems which is the fundamental paradigm of flat nonlinear systems.The obtained controllers can be directly used on the perturbed flat system in a universal controller fashion requiring only knowledge of the dimension of the nonlinear flat system.The map is complemented with the relevant references where the intermediate techniques were illustrated with the help of experimental results.

Section 2 introduces flatness and formulates the problem of controlling a flat output under unknown,timevarying,lumped input disturbances constituted by endogenous(state dependent)inputs and exogenous inputs.Section 3 illustrates the use of GPI observers and its relevance in the control of uncertain input-output models of flat systems and assesses the performance of the estimator in frequency domain terms.Section 4 explains GPI control in the context of an unperturbed chain of integrations.Section 5 places the uncertain control problem for flat systems in the context of robust FF’s.Section 6 contains the equivalence of reduced order extended observers,for disturbance estimation in an ADRC scheme,with the FF approach.

To simplify the presentation,only the SISO nonlinear case will be treated throughout.Extension to MIMO flat systems,linearizable via static or dynamic feedback,is not particularly difficult.All technical assumptions are to be considered globally valid in the relevant state or phase space.For convenience,we only treat flat output stabilization problems.The results trivially extend to flat output reference trajectory tracking problems.

2 Flat systems

Ann-dimensional,smooth,nonlinear system of the form:x=f(x,u),y=h(x),withx∈Rn,y∈R andu∈R,is said to beflat,with flat outputy∈R,if there exists a diffeomorphic mapand a smooth function ψi.e.,

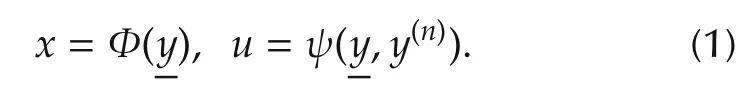
Φis said to differentially parameterize thencomponents of the statex.We assume thatThe state de-pendent input coordinate transformation:u=ψ,v),confirms that the original system is equivalent to the pure integration,controllable,linear system,y(n)=v.The relationu=ψ,y(n))is addressed as the input-(flat)output description of the system,or simply,the input-output system.

The vast majority of examples of flat systems include the affine in the control input case:=f(x)+g(x)u,y=h(x),with(f,g)a smooth pair of complete vector fields defined on the tangent space of Rn.The input-output description of the nonlinear,affine in the control,flat system is readily determined by

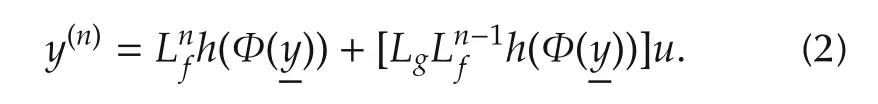
It will be assumed that the nonlinear input gain:is nonzero in a sufficiently large open subset of Rn.If nothing is specified aboutthe previous regularity assumption will hold globally in Rn.

Many engineering SISO nonlinear systems are flat(DC-to-DC converters such as the boost,the buck and the buck-boost converters;electric motors,such as DC motors,induction motors,variable reluctance motors,and permanent magnet synchronous motors;Airplane models,PVTOL systems,helicopters,some drones and marine vessels models).Many popular underactuated mechanical systems(ball and beam,inverted pendulum on a cart,the Furuta pendulum,the Kapitsa pendulum,etc.)are,generally speaking,non flat.

Suppose,for a moment,that the termnotprecisely known,or difficult to “wire-up”in an experimental implementation of a certain output feedback control law strategy,implying its“exact cancellation”.Contrary to this,assume also that the input gain,is perfectly known.The termviewed as an unknown scalar time function:is then properly regarded as anendogenous perturbationinput.Any external,unstructured,perturbation input,affecting the system’s state model,actsasamatchedperturbation inputin the inputoutput model and it is addressed as theexogenous perturbation,denoted by ϑ(t).The total perturbation input is,hence,defined as ξ(t)= η(t)+ ϑ(t).We consider then thesimplified modelas the perturbed integration system,

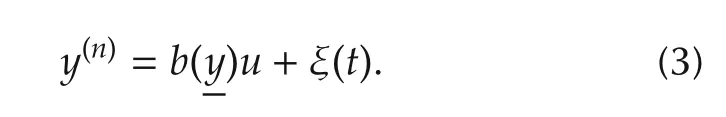
Flatness clearly leads,in a natural manner,to the paradigmatic perturbed model customarily considered in ADRC.Endogenous and exogenous perturbation inputs are handled as the total additive perturbation input.Particularly simple regular cases include:constant input gain:b)=b,output dependent input gain,b()=b(y).The general regular case,b()≠0,is treated via a suitable homotopic equivalence of the closed-loop output solution trajectories with those pertaining unit input gain,trivially stable,closed-loop output trajectories.This uses a globally well defined,state-dependent,time coordinate transformation.In such cases,b(,t),is largely unknown except,possibly,for its(unchanging)sign.

Let,without loss of generality,b((t))＞0 uniformly in time.Consider the implicit state-dependent time coordinate transformation,

with the corresponding differential equation exhibiting the trivial initial conditions:τ(0)=0.This defines a statede pendent time scaling transformationt→τ.Sinceis uniformly strictly positive,the solution trajectory,τ(t),is uniformly increasing,thus qualifying as a time-like variable.The transformation τ :t→ τ,represented by the solution of the differential equation for τ,is,hence,globally invertible on the non-negative portion of R,denoted by R+.The time transformed system is

For any static,or dynamic,feedback control lawu(such as ADRC),and any given set of initial conditions for the phase variables,(0),the trajectory,in the flat output phase space of the original system,is a smooth map,:R+→ Rn,defined by:t→(t).The corresponding phase space trajectory,τ→(τ),of the pure integration system,starting from the same initial condition,is a continuous deformation of that of the original system.In fact,the two maps:t→(t)and τ→(τ)belong to the samehomotopyclass.

Indeed,considerthemapz:[0,1]×R+→Rndefined by This map,continuously deforms phase space trajectories,t→(t),of the nonlinear flat system into phase space trajectories,t→(τ(t)),of the simplified system.The monotonicity of the function τ(t),with τ(0)=0,guarantee thatare the same.Since the phase trajectories for the original and the timescaled pure integration system start at the same initial condition,and end at the same point at infinity,the timescaling homotopy class existing between the trajectory maps is well defined.Trajectories homotopic,via time scale transformations,to stable trajectories are stable.

We,henceforth,consider,without loss of generality,pure integration systems of the form:

3 Generalized proportional integral observers

The flat system equivalence to a perturbed pure integration system,with unit control input gain,still requires,for robust feedback purposes,of the following two items 1)the asymptotic estimation of the phase variables set{y,,...,y(n−1)},simply denoted byand 2)the accurate estimation of the disturbance input ξ(t),as if it were an unstructured,purely time-varying,total disturbance input.It is clear that the prevailing linearity of the simpli fied system prompts,for the phasevaria bles estimation purposes,the use of a linear Luenberger type of observer and the incorporation of a reasonable total disturbance model for the signal ξ(t).Under the suitable disturbance smoothness assumption,anmth order Taylor time-polynomial approximation at timet,of the disturbance input,leads to the following self-updating linear approximation model:

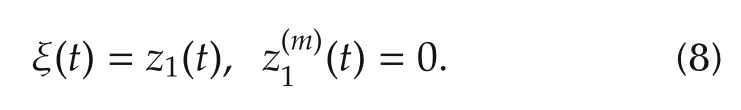
Definingzi(t)=z(i−1),i=1,2,...,m,we immediately obtain

The disturbance approximation model corresponds with an(m−1)st order time polynomial which ultra-locally will be made to act as a self-updating polynomial spline approximating the actual value of the disturbance input.This self-updating character is bestowed through the disturbance estimation errors in the following manner.

Define the simplified plant phase variables:yi=yi−1,i=1,2,...,n.Consider next the full order system model,including the disturbance model,and,also,its associated(perturbed)asymptotic extended observer:

The(redundant)output estimation error,ey=y−1,is seen to satisfy the following perturbed linear dynamics,

Clearly,the unperturbed version(ξ(t)=0)of the output estimation error dynamics can be specified to become asymptotically exponentially stable through the choice of suitable Hurwitz design coefficients:{λ0,...,λm+n−1}.Let ξ(s)denote the Laplace transform of the total disturbance signal ξ(t).The injected estimation error dynamics is described by the perturbed band-pass stable filter,

which enjoys infinite attenuation at very low,and at very high,frequencies.At intermediate frequencies,where the minimum disturbance attenuation(or,actually,disturbance amplification)may be experienced,a high gain observer design,based on corresponding Hurwitz coefficients:κi,i=0,1,...,m+n,definedby,λi= κi/∈m+n−i,i=0,1,...,m+n−1 substantially attenuates to a desired level themth derivative of the smooth total disturbance influence on the output estimation error and of its time derivatives.The parameter∈is a small positive real number.The frequency response of the output estimation error would be given,in normalized frequency terms,σ = ∈s,by

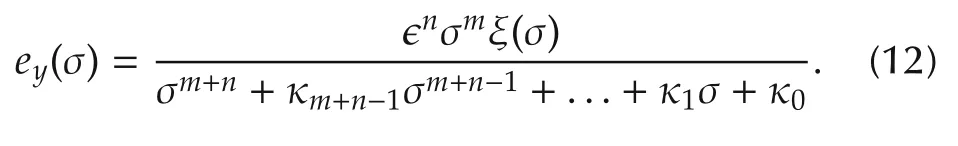
The attenuation effects of the high gain design parameter∈ are clearly depicted.

As a result,as∈is made sufficiently small,an uniformly absolutely bounded total perturbation input,with uniformly absolutely bounded time derivatives,induces a phase variable estimation error which can be made as small in magnitude as desired.Clearly,forj=0,1,...,n−1,

which still enjoys infinite,low and high frequency,attenuation features and modest attenuation at intermediate frequencies as the order of the output estimation error time derivative,j,increases from 0 towardsn−1.

The disturbance estimation erroreξ=ξ(t)−1is seen to satisfy,in the time domain,

As the estimation errors time derivatives,...,n,uniformly ultimately approach a neighborhood of the origin in the estimation error phase space,the disturbance estimation error,ξ−1,approaches a small neighborhood of the origin of the real line,still conveniently determined by the small parameter∈.

It should be clear by now,that the approximation error ξ(t)−z1,associated with the proposed Taylor polynomial model of the total disturbance,ξ(t),exhibits an explicit linear depen dance on the phase variable estimation errors.Forcing their contributions to be part of an(m+n)th order asymptotically exponentially stable linear dynamics perturbed by the distur bance model actual residual,the resulting disturbance estimate error automatically adapts to a small vicinity of zero,thus making the Taylor polynomial approximation truly self-adapting.

In the context of pure integration perturbed systems,GPI observers have been shown to be a generalization of Han’s extended state observer,but one which is also capable of on-line estimating a finite number of time derivatives of the total disturbance input.High gain state estimation seems to be at the heart of observer based ADRC control.

It was,therefore,rather natural to combine GPI observers in an ADRC scheme for simplified models of totally perturbed flat nonlinear systems.The estimated phase variables completed a suitable linear feedback loop with rather accurate,though approximate,disturbance cancellation.

4 GPI control:dynamical output feedback control without observers

The stabilization of a perturbed pure integration system can be accomplished by the use of suitable classical compensation networks.The lack of universality of classical compensation networks is determined,primarily,by the nature of the disturbance function,by the order of the plant and by the knowledge of the control input gain.There exists a very close connection between GPI control,based on integral phase variables reconstructors,and classical output compensation networks.The presence of additive exogenous and endogenous(total)disturbances disrupts the established input error integration process aimed to obtain structural estimates of the output phase variables.To circumvent this inconvenience,one must first establish the structure of the GPI output compensator,regardless of the additive disturbances and,then,proceed to examine,and assess,the closed-loop performance in the presence of such unknown but bounded perturbation inputs.

Consider then thenth order pure integration system as simplified from the input-to-flat output dynamics,

Iterated integrations of the inputuyield structural estimates of the phase variables as follows:

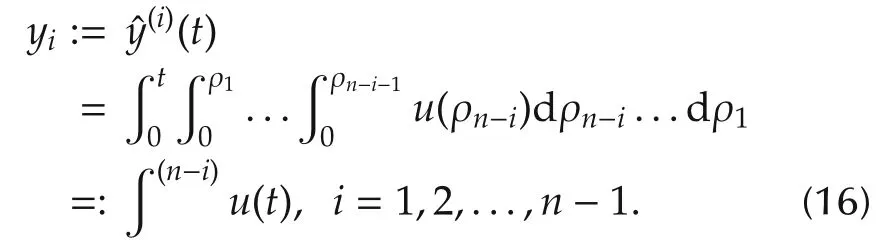
Each estimate is off by an(n−i−1)th order time polynomial,whose coefficients are exclusively dependent upon the unknown initial conditions associated with the estimated phase variable.Any linear feedback control scheme,based on the use of all these structural estimates of the phase variables(from the first,y1==(1),to the(n−1)th,yn−1=(n−1)),must dully compensate,as classically done,for the resulting linear combination of the corresponding time-polynomial errors.This simply requires a suitable linear combination of iterated integrals of the output signaly,ranging from a first order output integration,for compensation of the constant errors,up to an iterated(n−1)th order output iterated integration for the compensation of the(n−2)th order time polynomial associated with the estimationy1ofy=y(1).The linear control scheme,thus requires only the measurements of the input signaluand of the output signalyfor its implementation.

A compensator for the unperturbed chain of integrations is given by

In terms of the Laplace transforms,one obtains the implicit expression for the control inputu

Solving foru(s)we have

The closed-loop,unperturbed,system is readily obtained as

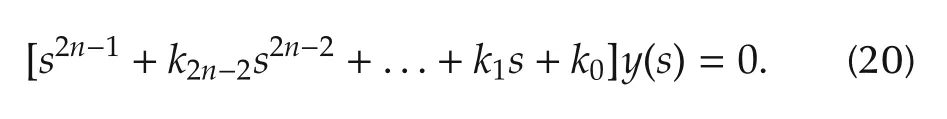
The order of the dynamic output feedback compensator,for the unperturbed input output dynamics,is one less than the order of the plant.The output can be exponentially asymptotically stabilized via the suitable choice of the design parameters,{k2n−2,...,k1,k0},as the coefficients of a(2n−1)degree Hurwitz polynomial in the complex variables.The above stabilizing classical compensation network is addressed as theGPI controller.

The above dynamic flat output feedback control scheme allows for flat output stabilization without explicitly using a linear observer exhibiting exponentially asymptotically stable(redundant)flat output estimation error.

5 Flat filters

The GPI controller is non robust with respect to additive disturbance inputs of the simplest kind(constant unknown disturbances,for example).As it was done in GPI observer based ADRC control of simplified,perturbed,flat systems,total additive disturbances may be modeled as finite order time polynomials(say,polynomials of orderm−1).There are,however,at least,two equivalent manners of bestowing the self updating feature to such a finite order,linear,total perturbation model.One of them is through exogenous input extensions,coupled with imposition of closed-loop stability for the entire extended systems.This is dual to the GPI observer approach.We take,however,the alternative route of compensating,in the feedback control,the effects of the total perturbation input through a suitable finite linear combination of iterated output integrations.

Consider the output feedback control law

Solving foru(s),after using the Laplace transform operator on the implicit controller expression,we obtain

The closed-loop system,in the absence of input disturbances,is given by

which can be made to asymptotically exponentially converge towards zero provided the appropriate(Hurwitz)gains are used.

For the perturbed pure integration system

The previously derived dynamic output feedback controller is directly used on the perturbed system.One obtains the following closed-loop system,driven by the total perturbation input.

(3)对接BEPS第13项行动计划成果，国内税法中引入转让定价国别报告法律制度。2016年6月，国家税务总局发布《关于完善关联申报和同期资料管理有关事项的公告》，引入了新的转让定价文档体系，更新了现行中国转让定价合规要求，具体涵括了国别报告在内的同期资料文档和纳税申报表的新要求，与BEPS第13项行动计划成果《转让定价同期资料和分国信息披露指引》的建议保持一致，为中国履行国别报告交换义务提供了国内法律保障。

The frequency response of the output stabilization error(represented byyitself)exhibits significantly large attenuation at low and high frequencies,thus rejecting high frequency measurement noise and rejecting also typical low frequency disturbance inputs.For intermediate frequencies,a high gain parameter factor,in the form:κ =ki/∈2n+m−1−i.This induces the normalized frequency relation,

6 Flat filters and observer based ADRC:An equivalence

Consider the pure integration perturbed system

We adopt,for the reduced order observer,then−1 dimensional system state representation including an artificial velocity measurement(y2==1):

A reduced order extended state observer(ROESO),which takesy2as the artificially measured output,including,also,mextra output integrations,is given by

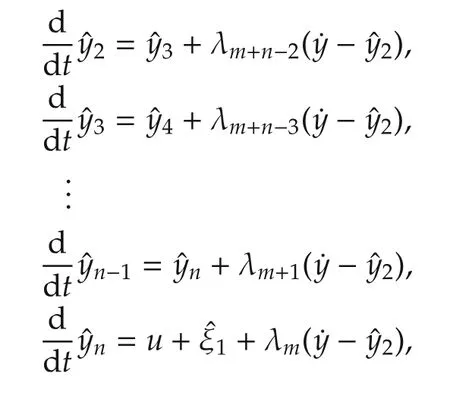
Define

The ROESO is thus proposed to be

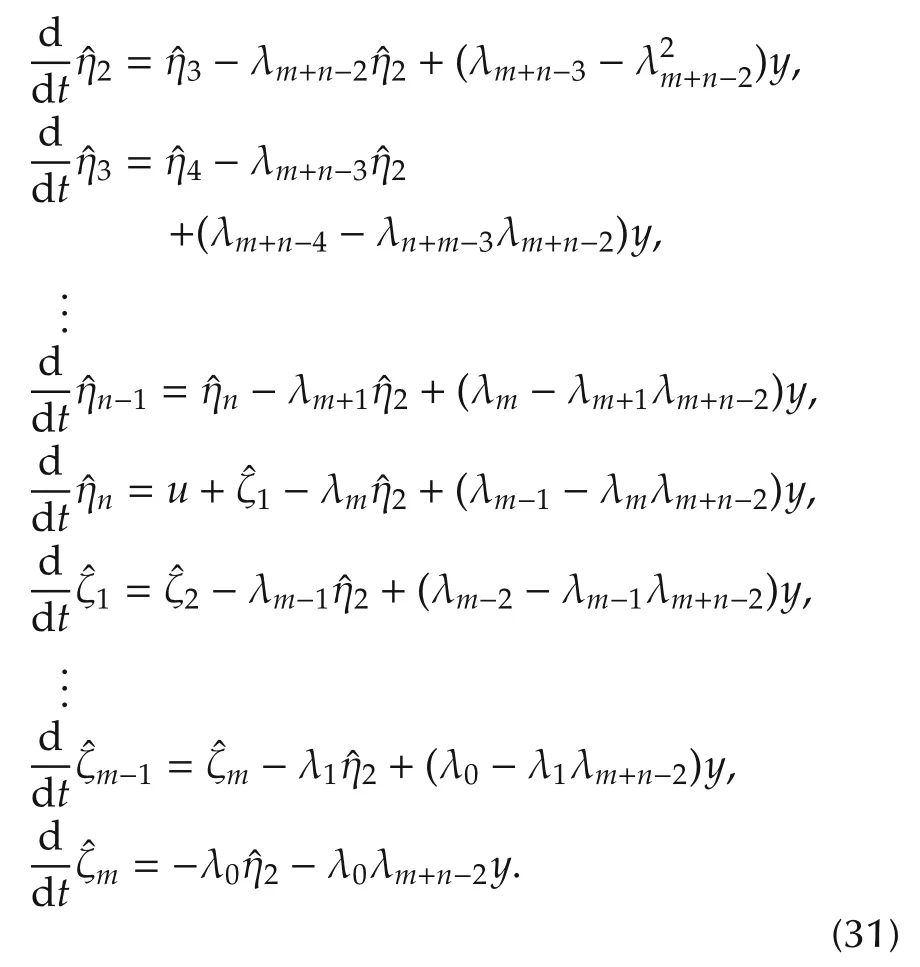
The estimates of the original phase variables may be computed from the following expressions:

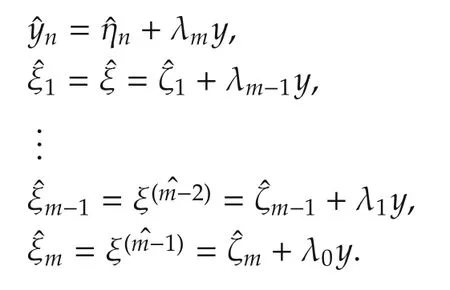
Defining also,for the original system,

with ξ1=ξ,ξ2=˙ξ,...,ξm=ξ(m−1).One readily obtains

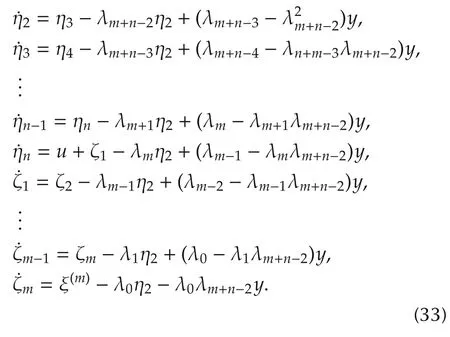
The ROESO state,and disturbance,estimation errors are seen to satisfy:

In other words,the estimation errore2satisfies the linear perturbed differential equation:

From here,it easily follows that,

which implies large attenuation of the low frequency input disturbance signal,ξ(t),in the state and disturbance estimation errors,produced by the proposed ROESO.

whereyjis the(j−1)th order time derivative of the outputy.

Thenth order time derivative of the output(itself the stabilization error)satisfies

Letq(s)denote the following characteristic polynomial:q(s)=sn+m−1+ λn+m−2sn+m−2+...+ λ1s+ λ0and letp(s)denote the closed-loop control characteristic polynomialp(s)=sn+ γn−1sn−1+...+ γ1s+ γ0.Using the above expressions,one obtains,in the Laplace transform domain:

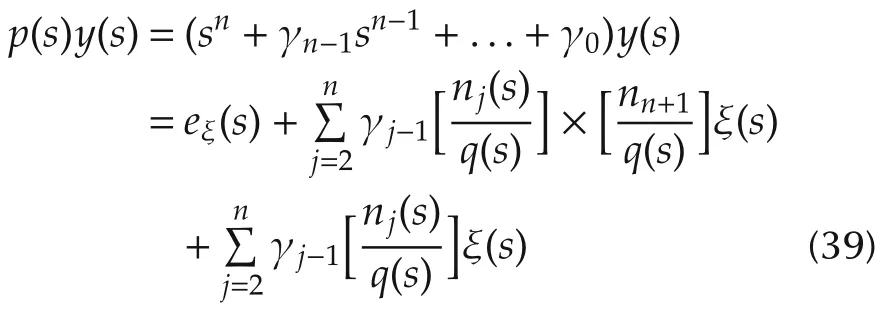
with

The closed-loop system output,y1,evolves,excited by the disturbance ξ,in accordance with the following dynamics:

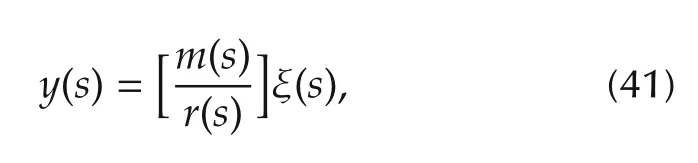
where

Clearly the denominatorr(s)is of the form,

while the numerator is of the form,

The characteristic polynomial of the closed-loop system factors into the product of the ROESO characteristic polynomial(i.e.,n+m−1=(n−1)+m)and thenth order characteristic polynomial of the closed-loop system,obtained by straightforward pole placement on thenth order pure integration plant system,as if all the phase variables had been available for feedback.All this is,evidently,in accordance with the observer controller design separation principle for state feedback through an observer in linear systems.

An output stabilization feedback controller for annth order pure integration system,y(n)=u+ξ(t),was found to be characterized,in the frequency domain,by

with the filter gains chosen to guarantee a Hurwitz closed-loop characteristic polynomial.The closed-loop system is described by

where

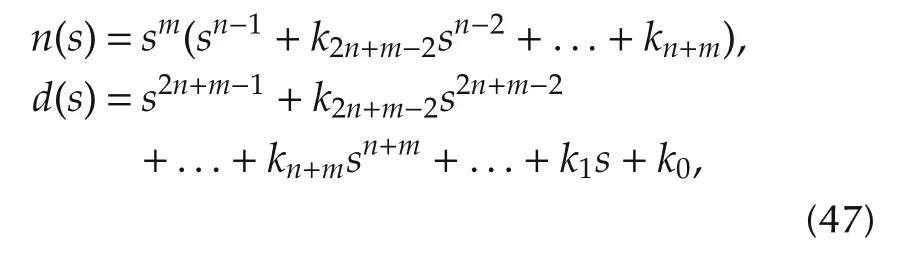
which is clearly identifiable with the ROESO-based ADRC closed-loop system,depicted in equation(41),thanks to the fact that the closed-loop characteristic polynomial coefficients uniquely determine all the coefficients in the flat filter controller.We therefore have

Clearly,given a ROESO-based ADRC controller design,there exists a unique stable flat filter controller which has exactly the same set of fundamental transfer functions(sensitivity,complementary sensitivity and open loop transfer functions).On the other hand,given a FF controller design,there exists non-unique equivalent ROESO based ADRC controllers.This one-way equivalence is substantially helpful in synthesizing observer based ADRC control schemes in the form of a single linear controller,in the form of a stable proper transfer function with enhanced disturbance attenuation features and good low frequency trajectory tracking features.The equivalence has been tested,also,in several experimental settings.

7 Conclusions

In this article,a roadmap,intimately related to the author’s gradual understanding,and linking,of ADRC with differential flatness and GPI control in the form of robust flat filters,has been provided through the basic developments leading from one end to the other.An exposition has been given of the inherent and natural relevance of differential flatness in the control of nonlinear uncertain systems for the SISO case.Also,the natural importance of classical compensation schemes in the control of uncertain nonlinear systems cannot be overemphasized.It is the author’s belief that the key issue,and one which encounters serious difficulties and criticisms on ADRC in the automatic control community,is given by the unstructured nature of the simplified pure integration system in the realm of non-linear control,whose design methods have been traditionally dominated by meticulous consideration of the nonlinear state structure.When the cult to the nonlinearities is swept away,in the form of a total purely time varying disturbance,all the arsenal of robust linear control can be readily applied to great advantage.It is my personal belief that ADRC still has numerous development avenues,both,in theory and practise,in comparison with other nonlinear control and observer design methods.

Acknowledgements

The author wishes to express his indebtedness to his colleages:V.Feliu-Battle,J.Linares Flores,R.Garrido-Moctezuma,M.Oliver-Salazar,M.Velasco-Villa,R.Castro-Linares,A.Rodríguez´Angeles,and M.Arteaga-P´erez,R.Morales,Z.Gao and C.Huang and C.Aguilar-Ibãnez for their kind cooperation in carrying out joint work on ADRC over the years in challenging areas of automatic control engineering.Former and actual Ph.D.and M.Sc.students:J.Cort´es-Romero,A.Luviano-Juarez,C.García-Rodríguez,M.RamírezNeria,E.Zurita-Bustamante,F.Gonzalez Montãnez,C.Lopez-Uribe,D.Rosales-Díaz,L.Cuevas-Ramírez,E.Herńandez-Flores,M.Aguilar-Orduna,for efficiently,and successfully,implementing,on laboratory experiments,results related to ADRC,while teaching him most of what he has been able to report on the topic.

8 Brief description of the bibliography

References[1–4]represent,in the form of books,the contributions towards flatness,GPI control,GPI observers and ADRC of the author,his coworkers and students.Numerous application examples and laboratory experiments are described in detail in those four references.References[5–11]are book chapters containing early work on GPI observers,flatness and GPI control.References[12–41]constitute journal articles,published since 2010,containing diverse applications of GPI observers,GPI controllers and flatness based controllers.In many of these works striking coincidences and similarities may be found with ADRC schemes,at a time the author of this article was unaware of the vast potentials and appeal of the fascinating research field started by Prof.J.Han.Meeting Prof.Z.Gao in 2013,completely changed the perspectives and triggered the enthusiasm of the author for this area,while feeling the respectful need to start calling things by their proper name.