驻室倾斜对引信后坐针刺发火机构发火正确性的影响
2018-11-02王永亮王雨时
王永亮,王雨时,闻 泉
(南京理工大学机械工程学院,江苏 南京 210094)
0 引言
引信后坐针刺发火机构是一种经典的机械惯性发火机构,其主要原理是靠发射时的后坐力即直线惯性力使击针相对火帽有足够的戳击动能戳击火帽而使其发火。由于其结构简单,目前仍广泛应用于射弹引信系统。
引信后坐针刺发火机构设计过程中必须考虑两点:一是在装卸、运输和装填等勤务处理过程中满足平时安全性;二是射弹发射时满足发火正确性,即通常所说的“发火正确性”。典型的后坐针刺发火机构轴线设计与引信系统轴线是平行或重合的。但是在后坐针刺发火机构零部件、引信其他相关零部件和弹体等制造过程中,由于受径向配合间隙以及垂直度等形位误差的影响,往往导致引信后坐针刺发火机构驻室轴线相对于射弹运动方向出现偏歪,即产生一定角度的倾斜。
文献[1]介绍了引信后坐保险机构相对于引信轴线斜置一定角度设置,可用来解决引信后坐保险机构安全与可靠解除保险之间的矛盾。文献[2]以冲击响应理论为基础,分别对运动零件是击针和火帽的两种情况,提出了后坐针刺发火机构优化设计的数学模型,并且对算例中的引信后坐针刺发火机构提出了改进方案。文献[3]指出由传统设计方法——能量法设计的引信后坐针刺发火机构,其平时安全性和发射时的发火正确性不易得到保证,从而提出了概率设计方法,使机构平时安全性与发射时的发火正确性相互协调,以满足规定的技术指标要求。文献[4]在考虑机械引信后坐针刺发火机构结构尺寸、工艺、性能等要求的基础上,建立了以最大安全落高和戳击速度为目标函数的有约束非线性多目标函数最优化数学模型。文献[5]列出了引信后坐针刺发火机构运动方程,并介绍了图解分析法、余弦简化法、直线简化法、直接积分法和相面图解法五种计算方法求得微分方程初值问题的解析解。文献[6] 应用刚体动力学理论和仿真软件ADAMS、LS-DYNA分析了引信经典弹性后坐保险机构和刚性后坐保险机构对不同后坐过载作用时间的响应特性,得到了不同后坐过载时间下两类后坐保险机构解除保险时间响应。文献[2—6]对引信后坐针刺发火机构进行的理论分析都是建立在其轴线与引信系统轴线平行或重合的基础上,并未考虑其驻室倾斜对引信后坐针刺发火机构发火正确性的影响。针对此问题,本文借鉴文献[1]的工作,通过理论分析和计算机仿真,提出驻室倾斜对引信后坐针刺发火机构发火正确性影响的计算方法,试图为引信后坐针刺发火机构发火正确性分析和生产质量控制提供参考。
1 驻室未倾斜时引信后坐针刺发火机构惯性发火过程动力学分析
如图1所示为炮弹引信后坐针刺发火机构。弹丸未运动时,击针簧有一定的预压量,其抗力作用于针刺火帽,针刺火帽另受螺塞的反作用力作用,处于平衡状态。驻室未倾斜时,引信后坐针刺发火机构发火原理如图2所示。在图1和图2所示的引信后坐针刺发火机构中,火帽在上,是相对运动件,而击针在下,相对静止。在实际应用中,还有另一类结构,就是击针与火帽位置互换,击针在上,发生相对运动,而火帽在下,相对静止。但这两类结构的力学原理和数学模型都是完全相同的。

图1 炮弹引信后坐针刺发火机构Fig. 1 An projectile fuze setback stab firing device

L-针刺火帽底端到击针尖的距离;弹丸运动加速度 图2 引信后坐针刺发火机构发火原理Fig. 2 The ignition principle of fuze setback stab firing device
弹丸在膛内加速运动时,在驻室未倾斜情况下引信后坐针刺发火机构的针刺火帽-击针簧质量系统相对于击针座暨引信体的运动方程为[7]:
(1)
式(1)中,x为针刺火帽相对击针发生的位移;m为针刺火帽质量;m1为击针簧质量;M为系统换算质量,是针刺火帽质量与击针簧质量的1/3之和;x为针刺火帽在t时刻相对于后坐针刺发火机构(击针座暨引信体)的位移;V为弹丸的运动速度;K为击针簧的刚度系数;λ0为击针簧的装配预压量;Ft为切线惯性力;Fc为离心惯性力;Ff为由切线惯性力Ft与离心惯性力Fc形成的驻室侧壁摩擦力;f为针刺火帽与驻室内壁表面的摩擦系数。
(2)
对于旋转弹引信和非旋转弹引信,引信后坐针刺发火机构均在最大膛压点之前工作结束。对于旋转弹引信,研究保险机构意外解除保险特性时将Ff取为0系保守估计,故可以忽略。而在研究后坐针刺发火机构发火正确性时将Ff取为0则系冒进估计,故不宜采取。此时Ff由离心惯性力FC和切线惯性力Ft的合力将针刺火帽压于驻室内壁而产生。由内弹道膛压曲线和弹丸速度曲线的变化规律可知,在内弹道的起始阶段,膛压曲线的斜率较弹丸速度曲线的斜率要大,即膛压上升得快,弹速增加得慢[5]。对于旋转弹引信,引信后坐针刺发火机构在最大膛压之前工作结束,这时弹速很小,离心惯性力Fc至少要比切线惯性力Ft小两个数量级,因此计算时可以去除离心惯性力Fc且不影响计算精度,即不考虑离心惯性力Fc的作用。此时引信后坐针刺发火机构的针刺火帽-击针簧质量系统的相对运动方程为:
(3)
式(3)中,ω为弹丸的旋转角速度;r0为针刺火帽轴到弹轴的偏心轴。
式(3)可化简为:
(4)
如果r0=0,则为中心配置的理想情况,此时无摩擦力。
直线运动后坐保险机构后坐保险件的运动方程与针刺火帽部件的上述运动方程完全相同。
2 驻室倾斜时引信后坐针刺发火机构惯性发火过程动力学分析
2.1 基于刚体动力学理论推导
假设引信轴线与弹丸旋转轴线和速度方向重合,按照引信后坐针刺发火机构驻室轴线相对于弹丸旋转轴线方位的不同,引信后坐针刺发火机构驻室轴线倾斜即与弹丸旋转轴线不平行或不重合有多种情形,不同情形的倾斜对引信后坐针刺发火机构发火正确性的影响不同,且差异较大。驻室倾斜对引信后坐针刺发火机构发火正确性的影响主要取决于切线惯性力Ft和后坐力F沿驻室轴线方向的分力以及所形成的摩擦力。
如图3所示,引信后坐针刺发火机构驻室轴线倾斜可根据驻室轴线、后坐力F和切线惯性力Ft是否在同一平面内分为两种情形。倾斜方位、角度α和旋转角速度一定时,后坐力F方向竖直向下、大小一定,切线惯性力Ft方向、大小一定,因此后坐力F和切线惯性力Ft的合力F2的方向、大小是一定的,F2与F形成的夹角β是一定的。此时驻室倾斜对引信后坐针刺发火机构发火正确性的影响取决于F2与驻室轴线之间的夹角角度大小,夹角越大,F2在驻室轴线方向的有效分力越小,对驻室内壁形成的正压力越大,因此形成的驻室侧壁摩擦力越大,对引信后坐针刺发火机构发火正确性的影响越大。当驻室轴线、后坐力F和切线惯性力Ft不在同一平面内时,倾斜角度α和F2与F形成的夹角β不在同一平面,此时F2与驻室轴线之间的夹角角度大小小于α+β;当驻室轴线、后坐力F和切线惯性力Ft在同一平面内时,倾斜角度α和F2与F形成的夹角β在同一平面,此时F2与驻室轴线之间的夹角角度大小等于α+β。因此当驻室轴线、后坐力F和切线惯性力Ft在同一平面内时,F2与驻室轴线之间的夹角角度最大,此时驻室倾斜对引信后坐针刺发火机构发火正确性的影响最为不利,如图3(a)所示。
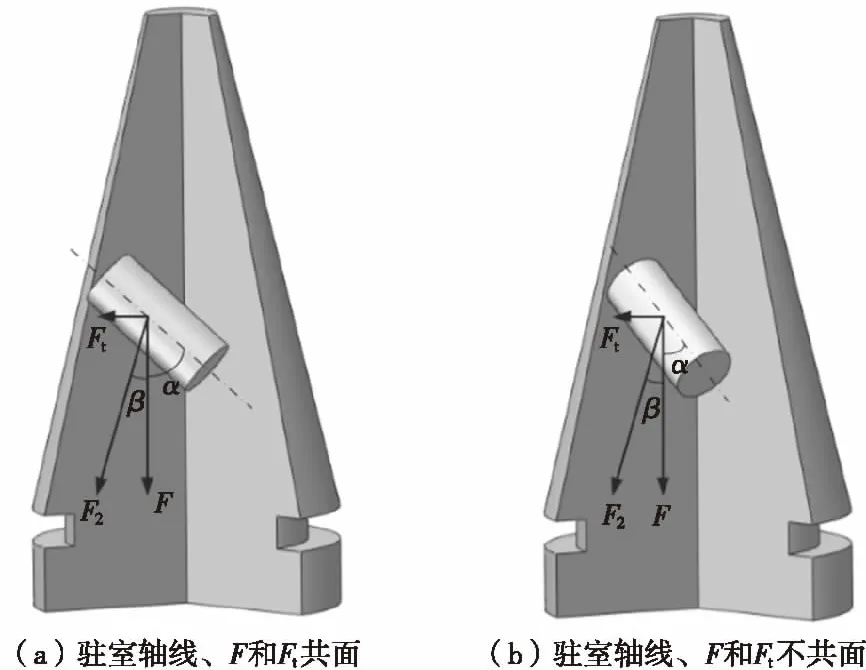
图3 引信后坐针刺发火机构在弹丸发射时受到的力Fig. 3 The force of fuze setback stab firing device during the launch of the projectile
此时,针刺火帽受力特性如图4所示。其中,F1为击针簧对针刺火帽的弹性抗力,FN是驻室侧壁对针刺火帽的正压力。

图4 驻室倾斜最不利情况下针刺火帽受力特性Fig. 4 The force characteristics of stab primer in the worst inner cavity tilt case
弹丸未运动时,击针簧有一定的预压量,其抗力作用于针刺火帽,针刺火帽在螺塞的反作用力作用下,处于平衡状态。
弹丸运动时,针刺火帽还会受到驻室侧壁支反力(包括正压力及其摩擦力)的作用,此时对针刺火帽进行受力分析,有
(5)
整理得引信后坐针刺发火机构的针刺火帽-击针簧质量系统的相对运动方程为:
(6)
取α=0,则式(6)与式(4)一致,式(6)的正确性得到了验证。
文献[8]给出炮弹旋转角速度ω和直线速度V的关系:
(7)
式(7)中,η为膛线的缠度。
(8)
则式(6)可化简为:
(9)
对于一般的线膛炮弹引信,为了简化分析计算过程,将膛压曲线的上升段用余弦规律近似表达,即
(10)
式(10)中,P为内弹道所提供的膛压,P0为挤进压力;Pm为最大膛压;tm为对应Pm的时间。
因此
(11)
式(11)中,D为弹丸的直径;M1为弹丸的质量;φ为虚拟系数。
因此,式(9)化简为:
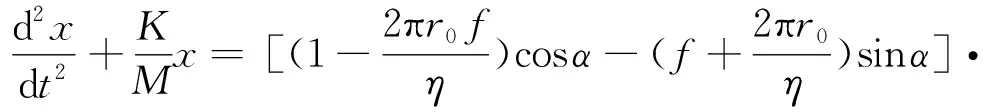
(12)
将式(12)化简得:
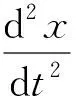
(13)
对式(13)求解得到:
(14)
利用初始条件:t=t0=0,x=0,dx/dt=0求出C1、C2并带入式(14)得:
(15)
因此针刺火帽的速度表达式为:
(16)
取x=L,可求出从开始运动到击针刺入针刺火帽深度为0时的运动时间tH和戳击速度vH。为保证后坐针刺发火机构可靠发火,必须满足[6]:

(17)
式(17)中,E=E0·exp(-0.1vH),其中E为火帽100%发火所需的动态发火能量;E0为按标准条件
试验时,火帽100%发火所需的能量。
2.2 算例分析
以37 mm口径人工防雹增雨弹引信为例,计算驻室倾斜对引信后坐针刺发火机构发火正确性的影响。
由火炮内弹道学理论提供的斯鲁豪茨基公式:
(18)
式(18)中,ωz为发射药质量;φ0为阻力系数。
又由
(19)
式(19)中,γ为膛线的缠角,该37 mm口径人工防雹增雨弹γ=5.88°。
已知该37 mm口径人工防雹增雨弹引信后坐针刺发火机构设计参数如表1所列。

表1 37 mm口径人工防雹增雨弹设计参数Tab.1 Design parameters of a 37 mm caliber artificial hail suppression and rainfall projectile
为了分别研究驻室倾斜角度α和针刺火帽与驻室内壁表面的摩擦系数f对引信后坐针刺发火机构发火正确性的影响,取f=0.25时,得到针刺火帽相对击针的位移在不同倾斜角度α下与作用时间的关系,如图5(a)所示;取α=5°时,得到针刺火帽相对击针的位移在不同摩擦系数f下与作用时间的关系,如图5(b)所示。
图5表明:针刺火帽与驻室内壁表面的摩擦系数f一定时,针刺火帽运动相同位移所用时间随着驻室倾斜角度α的增大而增大;驻室倾斜角度α一定时,针刺火帽运动相同位移所用时间随着针刺火帽与驻室内壁表面摩擦系数f的增大而增大。因此,驻室倾斜角度α和针刺火帽与驻室内壁表面的摩擦系数f对引信后坐针刺发火机构发火时间均有影响。
取f=0.25,得针刺火帽相对击针的速度在不同倾斜角度α下与作用时间关系,如图6(a)所示;取α=5°时,针刺火帽相对击针的速度在不同摩擦系数f下与作用时间的关系,如图6(b)所示。

图5 驻室倾斜时针刺火帽相对位移与作用时间关系Fig. 5 The relation between relative displacement and action time of stab primer with tilt inner cavity
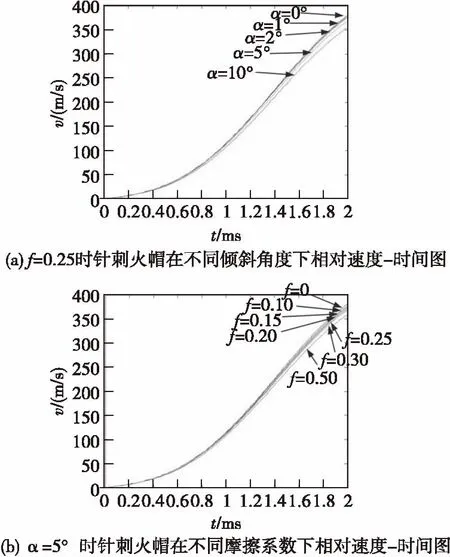
图6 驻室倾斜时针刺火帽相对速度与作用时间关系Fig. 6 The relation between relative speed and action time of stab primer with tilt inner cavity
图6表明,针刺火帽与驻室内壁表面的摩擦系数f一定时,针刺火帽在相同时间点的相对速度随着驻室倾斜角度α的增大而减小;驻室倾斜角度α一定时,针刺火帽在相同时间点的相对速度随着针刺火帽与驻室内壁表面的摩擦系数f的增大而减小。
该37 mm口径人工防雹增雨弹针刺火帽底端到击针针尖的距离L=6.25 mm,带入式(15)得:
用MATLAB软件求解得到针刺火帽与驻室内壁表面的摩擦系数f=0.25时,不同倾斜角度α下
针刺火帽从开始运动到击针刺入针刺火帽深度为0时的运动时间tH,如表2所列。

表2 f=0.25时不同倾斜角度下 针刺火帽运动时间Tab.2 f=0.25, movement time of stab primer at different tilt angles
由表2得引信后坐针刺发火机构发火时间随着倾斜角度的增大而增大。将上述数据带入式(16)求出针刺火帽在不同倾斜角度α下的戳击速度vH,如表3所列。

表3 f=0.25时不同倾斜角度下 针刺火帽戳击速度Tab.3 f=0.25, puncturing energy of stab primer at different tilt angles
由表3得驻室倾斜时针刺火帽戳击速度均小于未倾斜时截击速度,不利于引信后坐针刺发火机构可靠发火。驻室倾斜会导致发火时间增大,即针刺火帽加速时间增大,同时驻室倾斜也会导致针刺火帽加速度减小,因此针刺火帽截击速度变化取决于针刺火帽加速时间和加速度的变化量。
由文献[8]知该引信所用针刺火帽按标准条件试验时100%发火感度为1 000 g·cm,即E0=0.098 J,计算引信后坐针刺发火机构在不同倾斜角度下针刺火帽戳击动能W、火帽100%发火所需的动态发火能量E和相对未倾斜时动能减少量ΔW,如表4所列。

表4 f=0.25时不同倾斜角度下针刺火帽戳击动能和发火所需动态能量Tab.4 f=0.25, puncturing energy and the dynamic energy required for ignition of stab primer at different tilt angles
由表4得驻室倾斜角度α在[0,10°]区间内时,引信惯性针刺发火机构均能满足针刺发火要求。
用MATLAB软件求解得到驻室倾斜角度α=5°时,不同摩擦系数下针刺火帽从开始运动到击针刺入针刺火帽深度为0时的运动时间tH,如表5所列。

表5 α=5°时不同摩擦系数下针刺火帽运动时间Tab. 5 α=5°, movement time of stab primer at different friction coefficient
由表5得引信后坐针刺发火机构发火时间随着摩擦系数的增大而增大。将上述数据带入式(16)求出针刺火帽在不同倾斜角度α下的戳击速度vH,如表6所列。

表6 α=5°时不同摩擦系数下针刺火帽戳击速度Tab. 6 α=5°, puncturing energy of stab primer at different friction coefficient
由表6得针刺火帽与驻室内壁表面的摩擦系数f不同,戳击速度也不同,f=0时戳击速度最大。摩擦系数的增大会导致发火时间增长,即针刺火帽加速时间增长,同时摩擦系数增大也会导致针刺火帽加速度减小。
计算引信后坐针刺发火机构在不同摩擦系数下针刺火帽戳击动能W、火帽100%发火所需的动态发火能量E和相对摩擦系数为0.25时动能减少量ΔW,如表7所列。

表7 α=5°时不同摩擦系数下针刺火帽戳击动能和发火所需动态能量Tab. 7 α=5°, puncturing energy and the dynamic energy required for ignition of stab primer at different tilt angles
由表7得驻室摩擦系数f在[0,0.35]区间内时,引信惯性针刺发火机构均能满足针刺发火要求。
3 仿真验证结果分析
为进一步探究驻室倾斜角度α和针刺火帽与驻室内壁表面的摩擦系数f对引信后坐针刺发火机构发火时间和戳击动能的影响,与理论推导的结果对比,运用ADAMS软件对引信后坐针刺发火机构倾斜时的运动特性进行仿真分析。根据结构尺寸和作用原理建立相应的仿真模型,该模型由螺塞、针刺火帽、击针簧、击针和击针座组成,驻室未倾斜时模型如图7所示。设置螺塞、针刺火帽、击针和击针座材料属性,赋予其质量特性;设置弹簧属性,给k、λ0赋值,给针刺火帽添加移动副,并在移动副上设置摩擦特性。对驻室不同倾斜角度进行仿真分析时,只需将图7中螺塞、针刺火帽、击针簧和击针沿最不利倾斜方向倾斜预定角度重新建模即可;对针刺火帽与驻室内壁表面不同摩擦系数进行仿真分析时,只需改变摩擦特性中的摩擦系数即可。仿真分析时仿真参数与理论分析时各项设计参数相同。
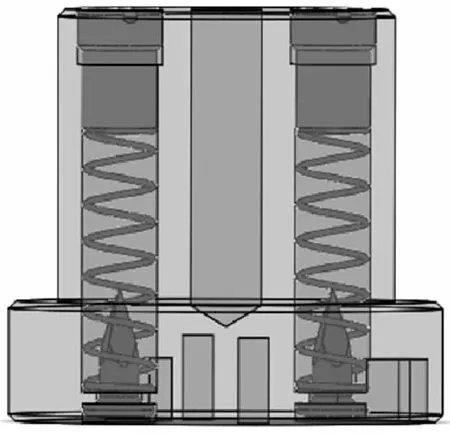
图7 仿真模型Fig. 7 The simulation model
对针刺火帽与驻室内壁表面的摩擦系数f=0.25,针刺火帽相对击针的位移L=6.25 mm时进行仿真分析,得到不同倾斜角度α对应的发火时间和戳击速度如表8和表9所列。

表8 f=0.25时不同倾斜角度下发火时间Tab. 8 f=0.25, ignition time at different tilt angles
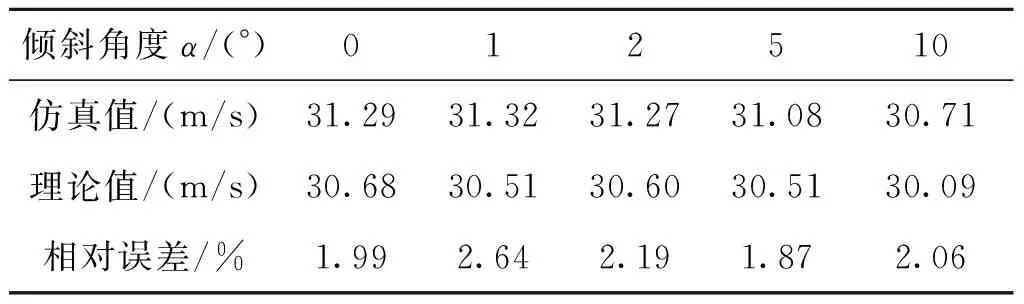
表9 f=0.25时不同倾斜角度下戳击速度Tab. 9 f=0.25, puncturing energy at different tilt angles
分析表8和表9数据可得理论结果与仿真结 果比较接近,相差均在3%之内,证明了理论分析的可信性。验证了驻室倾斜对引信后坐针刺发火机构发火时间和戳击速度均有影响,但影响不大,可以忽略。
4 结论
本文提出驻室倾斜对引信后坐针刺发火机构发火正确性影响的计算方法。该方法建立了引信后坐针刺发火机构驻室倾斜时发火时间和戳击能量的计算公式,并以37 mm口径人工防雹增雨弹引信为例进行理论计算和仿真分析,仿真分析结果与理论计算结果吻合较好,验证了理论计算公式的可信性。仿真分析和理论计算结果表明:引信后坐针刺发火机构驻室倾斜对发火时间和针刺火帽戳击动能造成影响,但影响不大。仍以37 mm口径人工防雹增雨弹引信为例,引信后坐针刺发火机构驻室倾斜10°、内壁与惯性体间摩擦系数0.25时,后坐戳击动能降低3.9%。引信后坐针刺发火机构发火能量设计应考虑此裕量。引信后坐针刺发火机构驻室内壁与惯性体之间的摩擦系数一定时,发火时间随着驻室倾斜角度的增大而增大,针刺火帽加速度随着驻室倾斜角度的增大而减小,针刺火帽截击动能的变化取决于针刺火帽加速时间和加速度的变化量;引信后坐针刺发火机构倾斜角度一定时,发火时间随着驻室内壁和惯性体之间的摩擦系数增大而增大,针刺火帽加速度随着驻室内壁和惯性体之间的摩擦系数的增大而减小,针刺火帽截击动能的变化取决于针刺火帽加速时间和加速度的变化量。这些结论为研究引信后坐针刺发火机构发火时间和戳击能量提供理论依据。
