“线性代数”信息化教学的探索

位瑞英，李 银

（韶关学院 数学与统计学院，广东 韶关 512005）

线性代数是高等数学中非常重要的一门课程，是大学本科计算机、管理、工程、经济等各专业必修的基础课，也是一门在很多领域中具有广泛应用的工具课程。在以往传统的课堂教学中，受制于课堂45分钟时间、硬件设施等方面的限制，授课重点通常放在理论知识的讲授上。自从2014年教育部关于地方本科高校转型发展的指导意见颁布以来，部分地方本科高校开始向应用型本科院校转型，作为大学数学核心课程的“线性代数”也面临着教学的改革和调整，克服重理论、轻实践的倾向，其一般的方式是信息的多元融合，融入教学辅助工具，将理论问题转化为数学实验问题的思路引入教学过程中［1-5］，再结合数学软件的功能，让学生掌握如何用数学软件进行相关计算的同时，加深对所学线性代数知识的理解。无论是从掌握一门实用技巧出发，还是从线性代数这门课程教学改革的意义出发，两者相结合实施教学都有可取之处，进而体现出地方应用型高校学生以“应用为驱动，学生为主导”的特点。

随着信息技术的飞速发展，基于开放、包容原则发展的数值实验呈排山倒海之势在快速改变着传统的一切。数学软件MATLAB以其具有的数值与符号计算、图像显示、文字处理以及强大的矩阵运算功能等特点受到广大师生的推崇，而线性代数中向量组的线性相关性，以及在它的基础上推导和衍生出的其他相关理论，如矩阵的运算、向量组的线性相关性的判定、线性方程组解的结构及求法、二次型等许多知识点都离不开矩阵。如何将MATLAB软件引入线性代数的教学中已经成为地方高校线性代数教学改革的一种趋势。一方面，能加深学生对理论知识的理解；另一方面，改进了传统的教学方式，也可以突出该学科与数学模型、数值分析等课程的联系，提高学生的动手能力及参与度，激发学习的兴趣，使学生对知识的获取、理解与掌握有重要的推动作用，从而达到“学练结合，学有所获，学以致用”的效果。

在传统的线性代数解题中，计算一个矩阵的秩、判断向量组线性相关性、求解方程组等知识点中，学生需要花很长时间，并且计算准确率不高。而利用现代教学方式与信息化软件融合的方式，将会大大缩短计算的时间，增加准确率，增加学生的学习兴趣。下面将以具体例子说明，首先给出常用的软件命令，见表1。

表1 常用的软件命令表

一、MATLAB在向量组线性相关性中的应用

例1求下列矩阵列向量组的一个最大无关组：

记矩阵 B的 4个列向量依次为 α1,α2,α3,α4，则α1,α2,α4是列向量组的一个最大无关组，且有α3=3α1-2α2。

解 编写程序如下：

说明 α1,α2,α3是 R3的一个基，且有 b1=5α1+α2+α3,坐标为(5,1,1)T。

二、利用MTALAB求解齐次线性方程组

例3 求解线性方程组：

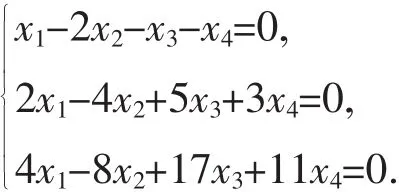
解 在MTALAB命令窗口输入程序：

＞＞A=［1-2-1-1;2-4 5 3;4-8 17 11］;

＞＞r=rank(A) %求系数矩阵的秩

＞＞y=null(A,‘r’) %求齐次方程组的基础解系

＞＞r=2， ξ1=(2,1,0,0)T,ξ2=(2,1,-5,7)T

结果分析：系数矩阵的秩小于未知数x的个数(rank（A）=2＜3)，根据相关判定定理可知，该齐次方程组有非零解，并且基础解系中有两个列向量；通过命令null(A,‘r’)，可以进一步得到该方程组的基础解系。

三、利用MTALAB解非齐次线性方程组

情况1 方程组解的存在性判断定理：若非齐次线性方程组系数矩阵A的秩不等于增广矩阵B的秩，则该方程组无解。

在MATLAB命令窗口运行以下命令：

＞＞A=［2 1-1 1;3-2 2-3;5 1-1 2;2-1 1-3］;%系数矩阵

＞＞b=［1;2;0;4］;%常数列向量

＞＞B=［A b］; %增广矩阵

＞＞rank(A),rank(B)%系数矩阵的秩及增广矩阵的秩

结果：rank（A）=3，rank（B）=4.

由于 rank（A）≠rank（B），故由解的存在性判断定理可知，该非齐次线性方程组无解。

情况2 方程组解的存在性判断定理：若非齐次线性方程组系数矩阵A的秩等于增广矩阵B的秩，同时又等于未知数x的个数，则该方程组有唯一解。

借助MATLAB软件求解，具体程序如下：

＞＞A=［1 3 5-4 0;1 3 2-2 1;1-2 1-1-1;1-4 1 1-1;1 2 1-1 1］;

＞＞b=［1;-1;3;3;-1］;

＞＞B=［A b］;

＞＞rank(A)

＞＞rank(B)

由于 rank（A）=rank（B）=4（未知数 x的个数），因此由解的存在性判断定理可知，该方程组有唯一解。

情况3 方程组解的存在性判断定理：如果系数矩阵A的秩等于增广矩阵B的秩，同时小于未知数x的个数，则该方程组有无穷多解。

编写MATLAB程序：

＞＞A=［2-1 4-3;1 0 1-1;3 1 1 0;7 0 7-3］;

＞＞b=［-4;-3;1;3］;

＞＞B=［A b］;

＞＞rank(A)

＞＞rank(B)

结果分析：矩阵A的秩等于矩阵B的秩=3＜4(未知数x的个数)，因此由解的存在性判断定理可知，该线性方程组有无穷多解。

四、MATLAB在相似矩阵及二次型中的应用

解 二次型矩阵为：

P就是所求的正交矩阵，使得PTAP=D，令X=PY，其中 X=［x1x4］T,Y=［y1y4］T，化简后的二次型为g=9+18+18。

上面求得的正交矩阵P是数值解，下面求正交矩阵的精确解。由命令可求：

此处v的第1、2、3列分别是所求得矩阵A的特征值9、18、18所对应的特征向量。然后对v化简，正交化与单位化处理，可求出正交矩阵P。

通过本文的案例可以看出，通过将数学实验软件MTALAB引入到线性代数的教学中，一方面有助于学生对知识的理解与巩固；另一方面改变了传统的教学方式，让学生更多的参与到教学讨论中，提高学生学习的效率和兴趣，也避免了手动将矩阵做行初等变换等一系列的计算过程，从而大大缩短了计算时间，增加了准确率，让学生在学习理论知识的同时了解了计算机的实用，并能熟练运用MTALAB软件解决线性代数中的问题，进而达到学有所用、学以致用，提高学生的综合素质的目的。

利用信息融合方法解决线性代数问题是现代教育研究课题之一，本文从线性代数的实际出发，借助信息技术与数学软件功能，辅助求出线性代数问题，形成了“讲授、板书、计算机演示”为一体的教学模式，从而丰富了线性代数问题的案例教学，并从实际意义和结果分析上，揭示实际学习中代数问题快速求解的重要意义。