基于小波分析的灰色SVM在变形预测中的应用

陆杰，覃书林，徐宁辉

(南宁勘察测绘地理信息院，广西 南宁 530001)

1 引 言

随着国家经济快速发展，变形预测已成为工程和自然灾害防灾减灾最直接、最重要的方法之一。定期对变形体进行监测，收集变形数据，分析变形规律，建立更为准确的变形预测模型，对保证人民生命财产安全具有重要的意义。针对这一问题，国内外许多学者已提出了多种方法，如时间序列模型、灰色模型、神经网络、支持向量机以及各种组合方法等[1～3]。然而，受多种因素共同作用的结果，滑坡或建筑物往往呈现出较强的非线性和随机性，给模型预测带来了难度，且每一种方法都存在自身的局限性，没有一种方法能够完全适应各种情况下的预测和分析。支持向量机[4](Support Vector Machines，SVM)作为一种新的人工智能学习方法，在解决小样本、非线性及高维模式识别等领域具有许多特有的优势，已在变形预测中得到广泛应用。因此，针对各单一预测模型存在的缺陷，许多学者展开了多模型融合预测的研究，取得了较好的结果[5～8]。然而，组合模型的思路往往局限于从原始变形序列本身探讨变形预测问题，通过对预测残差修正或各预测值组合加权方法实现变形的预测。这样的组合思路并没有从变形体自身的变形特点出发，忽略了变形体隐含的特征信息，不利于预测模型的推广和预测精度的提高。

基于上述研究，本文从时频挖掘出发，提出基于小波分析的灰色支持向量机变形预测新算法。算法主要研究如何从复杂的原始变形序列中提取出不同频率的特征信息，并针对各分量的特点，建立更为合适的灰色支持向量机预测模型。同时，考虑到SVM模型的参数优化问题，采用网格搜索法[9]进行寻优，该方法用于小样本数据预测时比遗传算法、混沌优化算法较有优势。经两个算例，并与灰色模型、BP神经网络和支持向量机对比分析，验证新算法的可行性和有效性。

2 基于小波分析的灰色支持向量机预测模型

2.1 小波分析

小波分析是现代分析方法中的一种强有力的工具，小波分析的核心内容为小波变换，傅里叶变换是小波变换的数学基础。小波变换的概念是在1983年由法国地球物理学家J.Morlet在分析处理地球物理勘探资料时提出来的，具有多尺度分析的功能。由于变形序列是通过实际观测得到的离散数据，用小波变换进行预处理，可以有效提取数据的特征信息。本文采用Daubechies小波对变形监测数据序列进行分解。其原理参考文献[10]。

2.2 灰色支持向量机预测模型

(1)灰色模型

灰色系统分析方法建模可以做到所需序列信息少，不用知道原始数据分布的先验特征，可以通过有限次的生成便可将杂乱无规律的序列转化为有规则、规律性较强的序列，建立生成序列和时间的关系函数模型。其方法和原理参考文献[11]。

(2)SVM模型

其模型如下[4，9]：

设一组样本训练集为{(xi，yi)|i=1，2，…，l|}，其中xi∈Rn，yi∈R，xi为n维输入向量，yi为输出向量。将样本通过非线性映射函数运算，从原空间映射到高位特征空间上，在高维特征空间中构造最优决策函数。

f(x)=WTφ(x)+b

(1)

式中，f(x)为估计函数，WT为权值向量，W∈Rn；φ(x)为核函数，φ(x)∈Rn；b偏置量，b∈R。W、b为待定系数。

引入结构风险函数，在优化问题的实现过程中，估计函数会被不敏感损失函数转化，而不敏感函数ε可以表示为：

(2)

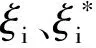
上述函数转化的过程中，应满足下面的约束条件：

(3)

为实现二次规划求解，利用对偶理论对其进行转化，则对偶式可表示为：

(4)

式中，拉格朗日乘子用a、a*表示；函数乘积用Q表示。

可将约束条件表示为：

Qij=K(xi，yj)=φ(xi)Tφ(xy)

(5)

式中，K(xi，yj)指的是支持向量机的核函数。

经过上述运算可将SVM的预测模型表示为：

(6)

由于SVM的性能很大程度上取决于核函数K(xi，yj)、核参数δ和正则化参数γ的选取。因此，选定能较好地反映模型复杂程度的径向基核函数作为SVM的核函数，采用网格搜索法进行最优参数的选取。

2.3 模型预测流程

本文采用db6小波对变形序列进行分解。根据已有的文献和资料，小波分解往往采用3层～5层较为适合。因此，本文将变形序列分解为4层，得到低频余量a3和高中频分量d1、d2、d3。设监测序列有n期，选取各分量和余量的前m期序列建立训练样本，后(n-m)期作为预测结果测试。由于d1、d2和d3分量往往具有一定的非线性和随机性，低频余量a3体现出趋势项的变化，因此，本文选取能够较好解决非线性问题的支持向量机模型和对线性问题具有较好预测能力的灰色模型进行预测，具体流程如图1所示。

图1 模型预测流程

3 算例分析

3.1 算例1

选取某滑坡9号监测点46期拉裂变形观测数据进行分析[12]，其垂直位移变形如图2所示。

图2 滑坡垂直位移序列

由图2可看出，滑坡位移变形总体呈现下降趋势，随机变化性较强，呈现非线性变化趋势，变形的最小值为 2.3 mm，最大值为 24.8 mm。直接采用传统的模型进行预测，不利于准确把握变形的规律。

因此，本文选取db6小波对原始序列进行4层分解，分解结果如图3所示。

从图3可看出，经小波分解得到的各分量能够更好地反映原序列的局部特征和变化趋势，具有较低的非线性和非平稳性特征。对比发现，d1、d2、d3分量明显趋于平稳，且频率依次降低，其中，d1预测分量表现了变形序列中的随机性，而d2、d3预测分量则反映序列中一定的周期性。余量a3属于低频部分，代表了变形序列中随时间变化的趋势。可见，经小波分解后各分量变化曲线比原变形序列曲线更光滑、更平稳，有利于下一步的建模预测和分析工作开展。

图3 小波分解结果

为验证本文算法的可行性、有效性和优越性，建立4种方案进行分析比较：方案1—灰色GM(1，1)模型；方案2—BP神经网络模型；方案3—支持向量机模型；方案4—本文算法。以前36期作为训练样本，后10期作为测试样本。其中，方案1～3直接采用原始数据建模，方案4采用经小波分解重构后的各分量建模，即支持向量机模型对d系列分量进行训练和预测，灰色模型对a3余量进行训练和预测。为了加快SVM的收敛速度和降低建模误差，将d系列分量归一化到[-1，1]区间，经模型预测后再还原到原始区间。对于支持向量机模型的参数选取，利用网格搜索法对惩罚参数c和核参数g进行寻优，设置δ和γ的选择范围和参数步长分别为：δ∈[2-8，28]，γ∈[2-8，28]；粗选步长为1，精选步长为0.5。

4种方案的预测结果对比如表1所示，图4反映了各模型的预测残差结果。

各模型预测结果对比表 表1

图4 各模型预测残差对比

由表1和图4可见：方案1对非线性变化的变形序列预测极不稳定，预测值呈线性变化，大部分预测值和实际值相差较大，最大、最小残差值分别为 5.370 mm、0.180 mm。方案2的预测结果优于灰色模型，但容易出现极大和极小值，最大残差值为 2.610 mm，最小残差值则为 -0.010 mm，总体预测结果依然不稳定。而方案3和本文算法对原始序列的预测结果都比较好，相对来说本文算法预测结果最好，残差曲线变化较为平缓，残差最大值为 0.292 mm，最小残差值仅为 0.004 mm。

3.2 算例2

为了进一步验证本文算法对突发变形预测的性能，以某大坝的0+119坝段具有代表性的DC01监测点垂直位移量[13]，如图5示。该变形序列共21期，监测时间从1996年7月开始，一直持续到1997年1月，观测频率为每个月3次。

由图5可以看出，大坝变形极其不稳定，具有较强的非线性变化趋势，前10期总体表现出有一定周期性的下降态势，后11期则总体表现出强随机性的上升态势，18期～21期更是持续急剧上升，且变形的最小值为 42.18 mm，最大值为 60.68 mm。可见该大坝变形随机变化性较强，采用传统的预测算法，很难得到较好的预测值数据。

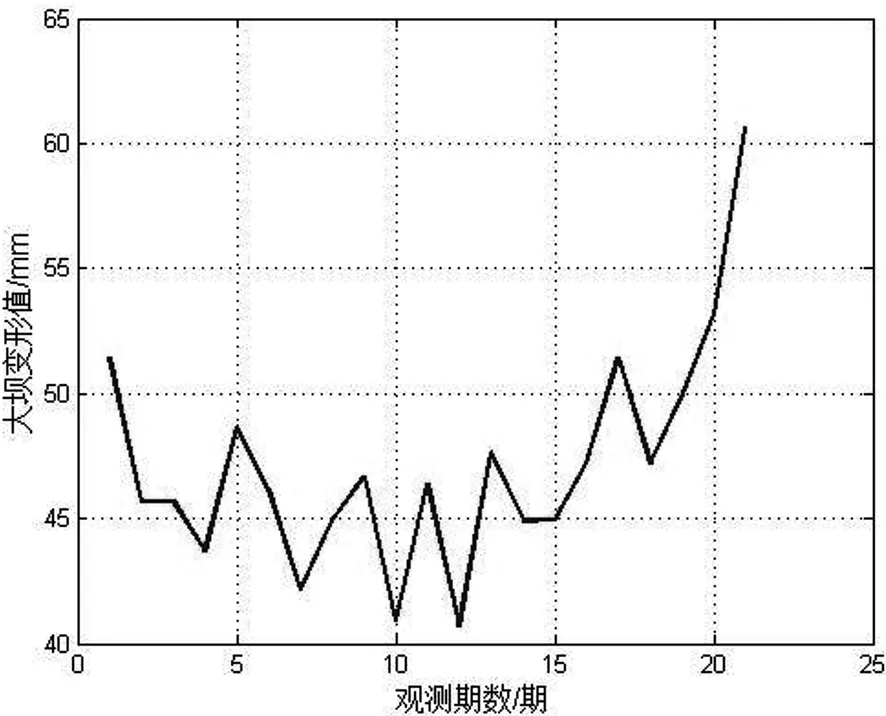
图5 大坝变形垂直位移序列

同算例1，选取db6小波对大坝变形原始序列进行分解，分解结果如图6所示。分别选取1期～16期数据作为训练样本，17期～21期数据作为测试样本，建模方法和算例1一样。各模型预测结果如表2所示，图7给出了各模型的预测残差曲线图。

图6 小波分解结果

各模型计算结果对比 表2

图7 各模型预测残差对比

由表2和图7可见，灰色模型和BP神经网络的预测结果极不稳定。在变形序列急剧变化的情况下，灰色模型的预测结果极不稳定，出现失真现象，特别是21期的预测结果已远远偏离监测值，无法找到变形规律；BP神经网络模型在监测值急剧上升阶段也出现了极大、极小值的情况；支持向量机模型的部分预测结果也不够稳定，预测的误差曲线呈线性递增。而本文算法的预测残差曲线较为平缓，残差最大值仅为 -0.300 mm，最小值为 -0.013 mm，预测精度远优于其他模型。

为了进一步综合评定本文算法的性能，采用均方根误差(RMSE)和平均绝对误差(MAE)两项精度指标进行评定，如表3所示。

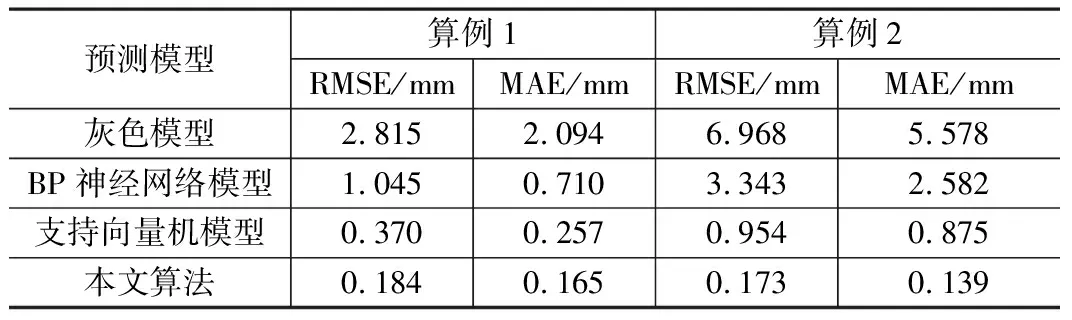
各模型计算结果对比 表3

由表3可知，灰色模型的预测精度最低，其次是BP神经网络模型，单一的支持向量机模型和本文模型的预测精度都表现出较好的预测精度，而本文算法的预测精度相较支持向量机有了进一步提高，均方根误差分别为 0.184 mm和 0.165 mm，平均绝对误差分别仅为 0.173 mm和 0.139 mm。可见，基于本文算法在一定程度上保证了较好的局部预测值和较优的全局预测精度。

4 结 论

本文将小波分析、灰色模型和支持向量机相结合引入到变形预测中，经理论和算例表明：①采用小波原理能有效分离出变形中隐含的非线性、随机性和趋向性特征信息，优化了原始信号，更好地反映变形的局部特征和变化趋势。②采用支持向量机和灰色原理相结合建立各分量预测模型，在一定程度上避免了灰色模型存在的理论缺陷，充分发挥了人工智能的优势，进一步提高了预测精度。考虑到仅从单一的变形序列本身建立多尺度预测模型，对于各种环境条件下的变形预测问题需要进一步的验证，如何将各特征信息与各影响因素相结合建立多尺度预测模型将是下一步研究的内容。