单芯光子晶体光纤边孔SPR折射率传感特性研究

彭荣荣，刘 彬，陈 佳

(1. 南昌工学院 基础教学部，南昌 330108；2. 南昌航空大学 江西省光电检测技术工程实验室，南昌 330063)

引 言

表面等离激元(surface plasmon polariton, SPP)是指在金属表面存在的自由振动的电子与光子相互作用产生的沿金属表面传播的电子疏密波。当入射光的频率与金属或掺杂半导体表面等离子体振荡频率匹配时就产生共振现象，称为金属表面等离子体共振(surface plasmon resonance,SPR)现象[1]。金属表面介质折射率对激发SPR的入射光频率非常敏感，利用这一特性可以制作基于SPR的折射率传感器件。该器件具有实时和快速检测、无需标记、耗样量少等特点，在生物和医药等领域具有广阔的应用前景，已成为近年来光学纳米传感技术的一个重要的研究热点[2-6]。SPR传感器已在许多传感结构中实现，如Kretschmann-Raether棱镜耦合、光学波导和光纤结构[7-13]等。在这些结构中，基于光纤的SPR传感器具有小型化、集成度高和可以实现远程传感等优点。近年来，随着光子晶体光纤(photonic crystal fiber, PCF)的出现，由于其具有无截止单模特性、高双折射、可控色散、高非线性、结构设计灵活可控等优良特性[14-21]，为纤芯模式与SPP模式相位匹配提供了新方式。PCF-SPR 传感器因其尺寸小、结构设计灵活、灵敏度高等优点，被广泛应用于生物学、医学、通信、材料学以及生命科学等各个领域，已成为国际上众多科研工作者的研究热点之一[22-23]。微孔内镀金属膜的光子晶体光纤 SPR传感器是现阶段研究的主要方向，HASSANI 等人提出了一种大孔内壁镀膜的光子晶体光纤SPR 传感器，传感器的分辨率可达10-4RIU[24]。2014年，GAO和GUAN等人又提出了一种基于金和TiO2复合膜的 PCF-SPR 传感器，折射率分辨率高达2.7×10-5RIU[25]。类似方法设计的 SPR 传感器还有光子晶体光纤选择性微孔镀膜结构和三孔光子晶体光纤结构等[26-27]。但是，大部分PCF-SPR传感器常常是采用多个临近的纳米金属孔结构[28-30]。多个金属纳米孔结构对于制备的成本和工艺要求较高，并且会降低信噪比，同时多个金属纳米孔直接很容易相互干扰，形成许多复杂的SPP模式。为了尽可能在比较宽的波长范围内，让纤芯基模只与单个SPP模式之间的耦合，提高折射率传感范围,作者提出一种在单芯光子晶体光纤纤芯内部设计旁侧椭圆分析孔的SPR传感结构。分析孔内壁涂覆金属纳米层(通常为金或银，其厚度为几十个纳米)，通过纤芯基模与分析孔SPP模式耦合，在相位匹配条件下达到共振耦合，实现对分析孔内介质折射率的SPR传感,并通过有限元软件COMSOL对其传感特性进行了数值计算和系统地分析。

1 理论模型

作者所设计的单芯光子晶体光纤SPR折射率传感模型的横截面结构如图1所示。光子晶体光纤空气孔以正三角形晶格排列，晶格常数Λ=2μm，空气孔直径d=0.5Λ=1μm，空气折射率n1=1，基底为二氧化硅折射率n2=1.45。在光子晶体光纤纤芯右侧引入椭圆待测孔，用以填充待分析物，设其折射率为na。外面的圆环为有限元仿真所需的完美匹配层(perfectly matched layers，PML)设置。采用椭圆孔设计是因为研究发现SPP高阶模式的数量会随着椭圆侧芯的椭圆率增大而受到一定的抑制[31]。椭圆孔中短轴L1=0.576μm，长轴L2=1.056μm。待测孔外层涂覆了银纳米层，厚度t=40nm。金属银相对介电常数由Lorentz-Drude模型方程给出[32]：

(1)

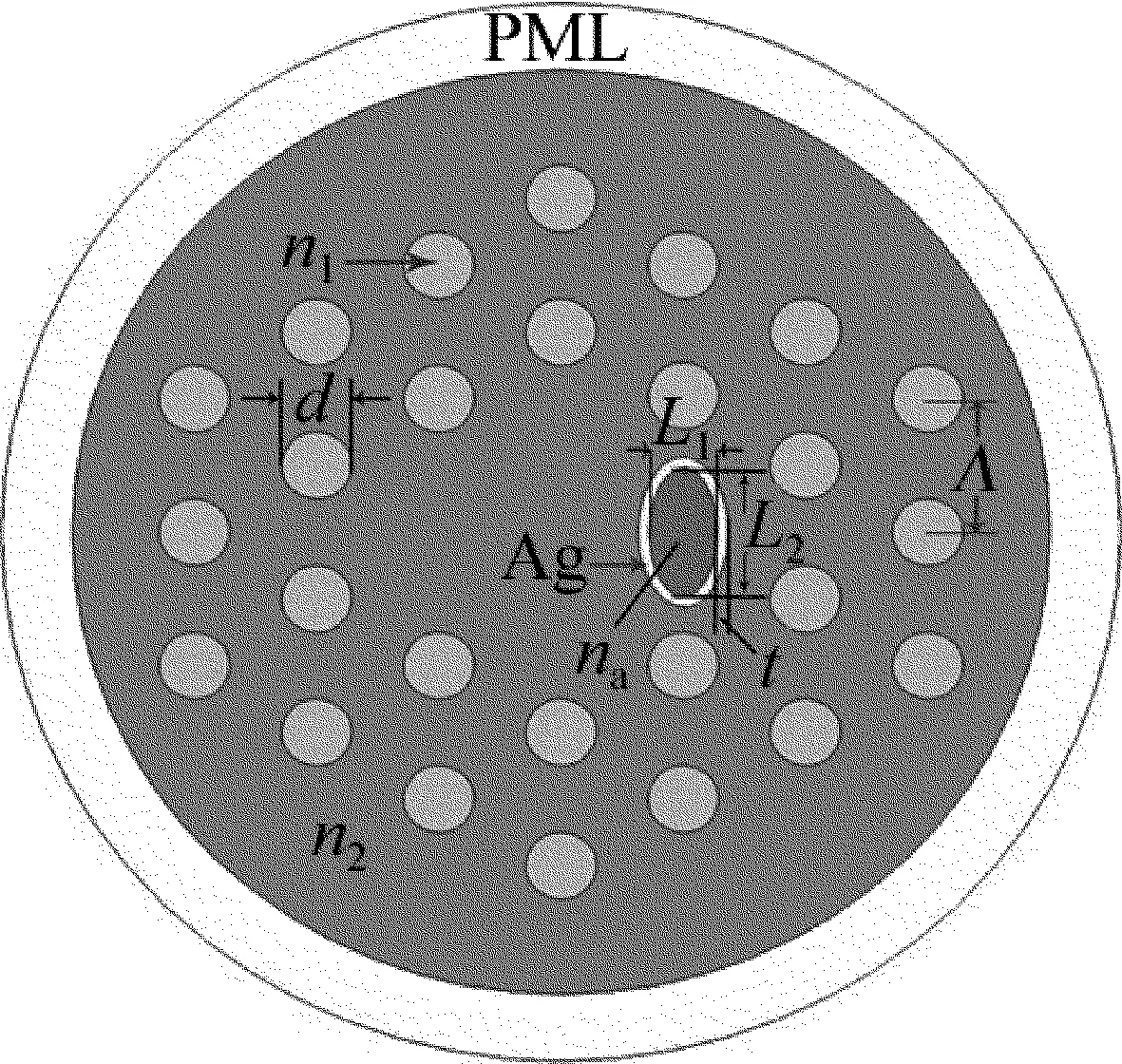
Fig.1 Cross section diagram of SPR sensor based on single-core photonic crystal fiber

式中，ε∞=1为频率无穷大条件下金属的介电常数；ω为入射光的角频率，ωm是共振频率，Ωm为等离子体频率，Gm为振子强度，Γm是阻尼因子，对应参量参照表1。

Table 1 Parameters in Lorentz-Drude model

2 传感特性分析

作者所设计的单芯光子晶体光纤结构具有双折射效应，纤芯的传导模具有x偏振和y偏振两个正交方向。人们前期的研究发现，一般x偏振纤芯基模能够有效与SPP模式耦合激发SPR，y偏振纤芯基模与SPP耦合效率很低。首先仿真分析不同偏振的传输模式与SPP模式耦合的情况。设na=1.43，通过COMSOL数值仿真得到波长在900nm～1450nm范围内，x偏振和y偏振纤芯基模和SPP模式相互耦合过程中的传输损耗曲线，如图2a所示。图2a中纵坐标表示有效折射率虚部，根据模式传输损耗公式[33]：

(2)

式中,neff为有效折射率，λ为入射光波长。可知，模式传输损耗正比于有效折射率虚部，因此可以通过有效折射率虚部的变化反应入射光的传输损耗情况，损耗值越大代表激发SPR越强。由图2a可以明显看到,x偏振纤芯基模与SPP模耦合过程中的传输损耗及所激发的SPR峰值更强，y偏振纤芯基模与SPP模耦合效率比较低。并且，前面研究结果也表明,y偏振纤芯基模与SPP模耦合激发的SPR共振对于分析孔内折射率的变化不敏感。所以主要研究x偏振纤芯基模与SPP模式耦合激发SPR的折射率传感特性。

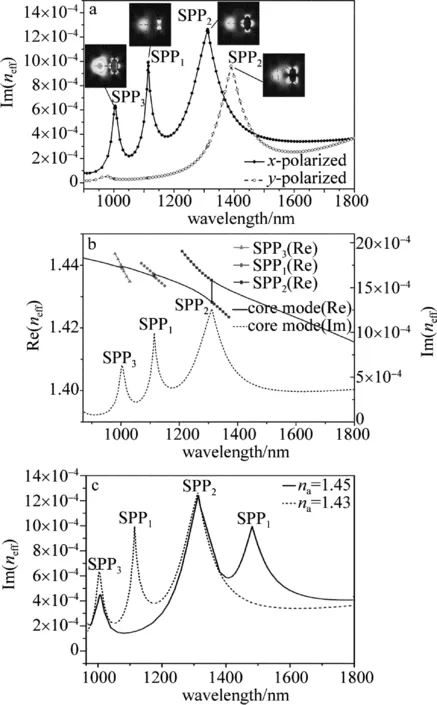
Fig.2 a—loss curves ofx-polarized andy-polarized core mode atna=1.43 and the optical distributions of SPR with SPP1, SPP2, and SPP3modes b—dispersion (left) and loss (right) curves ofx-polarized core mode and SPP modes atna=1.43 c—loss curves ofx-pola-rized core mode atna=1. 43 andna=1.45

计算入射光波长为900nm～1450nm时x偏振和y偏振光激发的纤芯基模和SPP模式的色散和损耗曲线。如图2b所示，发现在900nm～1800nm波段，椭圆待测孔区域存在3个不同的SPP模式，将其定义为SPP1,SPP2和SPP3模式。计算这3个SPP模式的折射率实部和虚部发现，3个SPP模式实部曲线分别与纤芯基膜的折射率实部曲线出现交叉现象，并且这个交叉点波长正好对应于纤芯基模(虚部)损耗特性曲线3个共振峰位置。也就是说，在这个波长位置纤芯基模波矢与SPP模式波矢相等，达到共振匹配条件，发生了SPR现象。其中SPP1和SPP3模式与纤芯基模折射率实部曲线直接相交，而SPP2模式与纤芯基模折射率实部曲线没有直接相交，而是形成抗交叉效应[34],并且这种抗交叉效应的耦合激发SPR效果优于直接交叉的情况，所以SPP2的损耗峰最强。分别计算这个3个SPP模式的模场分布，如图2b所示，发现SPP1模式的模场分布大部分局域在椭圆待测孔内部，这样可以有效地与待测介质接触，实现对待测介质的折射率传感。

接下来，数值计算了分析孔中介质折射率分别为1.43和1.45时纤芯基模损耗随入射波长变化情况，如图2c所示。可以看到，虽然与纤芯基模与SPP2耦合激发的表面等离子体共振最强(损耗峰最大)，但是光场并没有分布在分析孔中，所以分析孔介质折射率变化并没有改变损耗峰的位置，不适合用于传感。同样的，纤芯基模与SPP3耦合的损耗峰最弱，而且光场没有分布在分析孔中，所以分析孔介质折射率变化也没有改变损耗峰的位置，不适合传感。而SPP1模场主要集中在分析孔中，纤芯基模与SPP1模激发的SPR共振峰对于分析孔介质折射率变化非常敏感，可以具有很高的折射率传感灵敏度。

下面主要讨论SPP1模式与纤芯基模耦合激发表面等离子共振波长随分析孔中介质折射率变化的关系。通过有限元法数值计算分析孔中介质折射率na从1.37～1.47变化过程中SPP1模式与纤芯基模耦合激发SPR损耗峰的变化情况，如图3a所示。可以看到,随着分析孔中介质折射率的增大，所激发SPR的损耗峰呈现明显的红移现象。同时计算SPR损耗峰的波长随分析孔介质折射率在1.36～1.55范围内的变化曲线，如图3b所示。折射率传感灵敏度公式为：

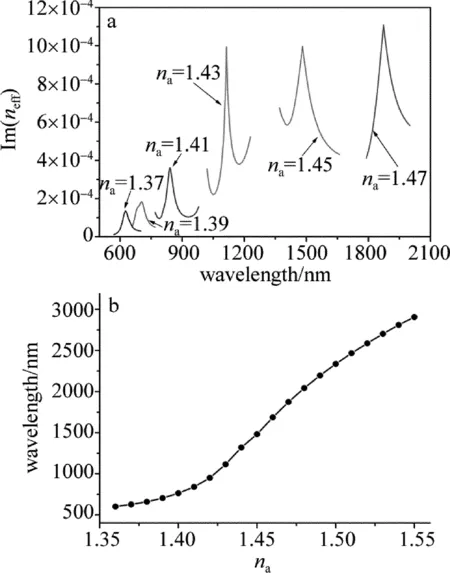
Fig.3 a—loss cures of core mode withnain the range of 1.37 to 1.47 b—relationship between resonant wavelength andna

Sλ[nm/RIU]=ΔλRW(na)/Δna

(3)

式中,ΔλRW为共振波峰波长变化，计算出折射率在1.36～1.55范围总的传感灵敏度为12139nm/RIU。参考D型光纤SPR传感器实验方面的研究，通过侧面抛光单模光纤5mm的SPR传感头实现了4365.5nm/RIU的传感灵敏度[35]。可以估计所设计传感器结构大约只需要光子晶体光纤传感头长度5mm～10mm就可以实现理论仿真计算的折射率传感灵敏度。

从图3b中可以看到,传感曲线出现明显的线性分段情况，不同分段曲线的灵敏度差异很大。在折射率1.36～1.42区域的传感曲线比较平缓，图4a中对其传感曲线进行了线性拟合，计算出该区域的线性传感灵敏度为5646.4nm/RIU，线性度为0.9317。而折射率1.42～1.57区域的传感曲线明显比较陡峭，图4b中对其传感曲线进行了线性拟合，计算出该区域的传感灵敏度为15326.8nm/RIU，线性度为0.98738。可以看到,折射率1.42～1.57区域的传感灵敏度和线性度都要明显优于1.36～1.42区域。

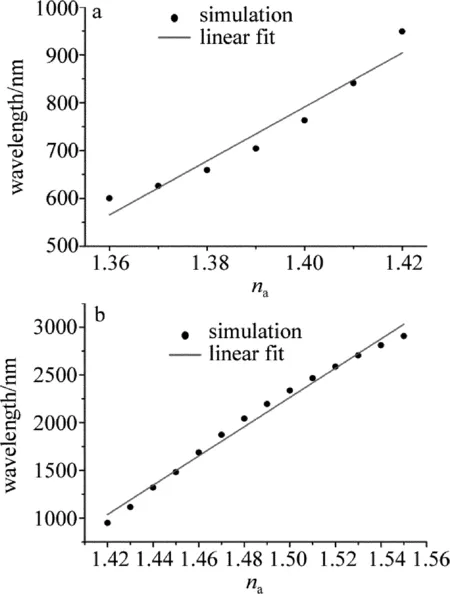
Fig.4 Linear fit curve of resonant wavelength

a—withnain the range of 1.36 to 1.42 b—withnain the range of 1.42 to 1.57

另外还数值计算了SPR峰损耗随分析孔内折射率的变化曲线，如图5所示。可以看到，大部分区间里，SPR峰的损耗也随着分析孔介质折射率的增大而增大。只有在折射率1.42～1.45的范围内，SPR峰的损耗才发生了突变的情况。重新观察图2b和图2c，发现其原因是纤芯基模与SPP1模耦合激发的SPR，其共振波长随折射率从1.43变化到1.45的过程中经过SPP2模式，而纤芯基模与SPP2模所激发的SPR共振峰的损耗是比较大的，所以形成了对用于传感的SPR共振峰损耗的干扰。在远离SPP2模式的折射率范围1.45～1.55内， SPR共振峰损耗随着分析孔折射率呈现线性变化。

Fig.5 Loss curves of SPR wavelength withnain the range of 1.37 to 1.47

3 结 论

通过有限元方法数值计算和分析了基于大纤芯的单芯光子晶体光纤椭圆边孔SPR折射率传感结构。该结构中纤芯模式与SPP模式同处于光子晶体光纤的纤芯位置，可以有效增强SPP模式与纤芯模式相互耦合的重叠区域。并且椭圆结构分析孔设计避免了多个SPP模式间的相互干扰。因此，在比较宽的折射率范围内(1.36～1.55)可以实现对分析孔分析物折射率的SPR传感，平均传感灵敏度达12139nm/RIU。另外，对其传感曲线线性分段情况进行分析：在折射率1.36～1.42区域，线性传感灵敏度为5646.4nm/RIU，线性度为0.9317；而在折射率1.42～1.57区域传感灵敏度达到15326.8nm/RIU，线性度为0.98738。研究结果对于提高光子晶体光纤SPR传感器的传感性能具有一定的应用价值。