考虑拥堵关联的城市主干道运行可靠性建模*
2018-11-01董可然朱自博封春房唐克双
董可然 朱自博 封春房 唐克双
(公安部交通管理科学研究所1) 无锡 214151) (同济大学道路与交通工程教育部重点实验室2) 上海 201804)
0 引 言
近年来,越来越多的学者将路段行程时间相关性引入主干道行程时间可靠性模型中.根据分析方法的不同可将相关文献归纳为基于交通流解析的方法和基于数理统计的方法两类.
基于交通流解析的方法能够深入分析主干道行程时间可靠性的内在机理,清楚的了解影响行程时间可靠性的因素.Zheng等[1]针对交通流随机特性,基于冲击波理论和排队论,提出了主干道车辆间的行程时间分布解析模型,着重考虑了车辆随机到达和离开过程及信号协调的影响.又在该模型中增加了排队溢出的影响,结果表明,在短间距交叉口和不同协调相位情况下,行程时间分布估计考虑溢出是非常有必要的.林徐勋等[2]基于交通流动力学,提出了基于随机松弛时间的行程时间可靠性计算模型,量化了交通流内部车辆间相互干扰对行程时间可靠性的影响.
基于数理统计的方法主要着眼于建立主干道行程时间分布的统计模型.He等[3]认为路段行程时间在空间范围上是不独立的,并通过相邻路段的样本点量化了行程时间的相关系数(correlation coefficient),结果表明同时考虑路段间行程时间相关性与各路段实际行程时间分布可更好的拟合干道路径行程时间分布.Feng[4]将主干道路段直行车辆的行程时间划分为不同状态,采用不同的分布近似拟合,并通过Markov Chain建立了路径中各路段行程时间的关联性,结果表明该模型可准确估计路径行程时间.启发式网格聚类方法(heuristic grid clustering method)确定连续路段之间状态的相关性,通过所有Markov Chain过程与对应的路径行程时间分布的加权叠加估计主干道路径行程时间分布.熊志华[5]将行程时间可靠性中的路段间的相关性划分为不相互影响、同步影响以及弱影响三种模式,并通过蒙特卡洛仿真分析表明在不考虑路段相关性情况下会高估行程时间的可靠度.
综上所述,国内外学者对城市主干道行程时间可靠性建模进行了大量研究,然而结合我国城市主干道运行特征与实证数据的研究还很少,并且现有的主干道路段行程时间相关性模型多建立在Markov Chain状态转移矩阵基础上,受到Markov Chain无后效性的限制,只能评价相邻路段间行程时间相关性,有必要基于拥堵关联模型对行程时间相关性的空间范围进行拓展.因此,本文分析了畅通、拥挤和拥堵(包括自发性拥堵和诱发性拥堵)等不同交通状态下行程时间分布特征,并构建了考虑交通拥堵发生概率和各路段间拥堵关联性的行程时间可靠性模型,以准确描述和分析城市主干道运行可靠性[6].
1 实证数据采集与处理
实证数据来源于山东省青岛市市南区的一条重要主干道——福州南路,长约1.3 km,共包含7个信号控制交叉口.该路段范围具有相交支路流量小、路侧出入口少、机非隔离等优点,可降低非交通流因素对研究路段交通运行的干扰.以直行车道组为研究对象,路段长度在160~320 m.研究方向从南至北,全段限速为50 km/h.
微波雷达检测器和卡口电警采集的数据为本文数据源.研究主干道的检测器分布位置见图1.其中,微波雷达检测器主要采集车道位置、分车型流量、速度、占有率等,卡口电警通过车辆匹配获得车辆通过任意两个设备间的行程时间.采集的数据为期2个月,覆盖全天时段,微波雷达检测器共约300万条数据,卡口电警共约1 200万条数据.

图1 研究城市主干道检测器分布位置
为了保证分析精度,本文对原始数据进行了清洗与修补等预处理,并集计成5 min间隔数据.根据预处理后数据缺失情况,最终选择了17 d数据,研究时段为06:30—22:30.
行程时间是本文交通状态评价和运行可靠性分析的依据,为获得各路段的行程时间,采用多源数据融合的方法,通过各路段定点检测器点速度确定对应权值,对两端卡口电警获得的总行程时间进行切分.并将得到的路段行程时间转算成行程速度,与设定的阈值比较,判断各路段交通状态.本文主要根据K-均值算法,得到交通状态对应的行程速度阈值分别为:拥堵[0,16)、拥挤[16,22)、畅通≥22(单位km/h).
图2以黑、银、灰分别代表拥堵、拥挤、畅通三种状态,展示了福州南路2015年10月29日研究时段(06:30—22:30)共192个5 min间隔的拥堵时空特征.从图中可知,拥堵在时间、空间两个方向上带状分布明显,即拥堵呈现出在时间上持续与在空间上扩散的特征.图中矩形框表明福州南路拥堵可近似分成三个区段:第一个区段是闽江路-江西路首先发生拥堵,然后蔓延至漳州一路-闽江路;第二个区段是漳浦路-漳州一路发生拥堵逐渐蔓延至漳州二路-漳浦路、香港中路-漳州二路;第三个区段是东海西路-香港中路.此外,对于三个区段中上游路段的拥堵消散时刻普遍早于下游路段.这表明主干道拥堵扩散有明显的拥堵关联现象.
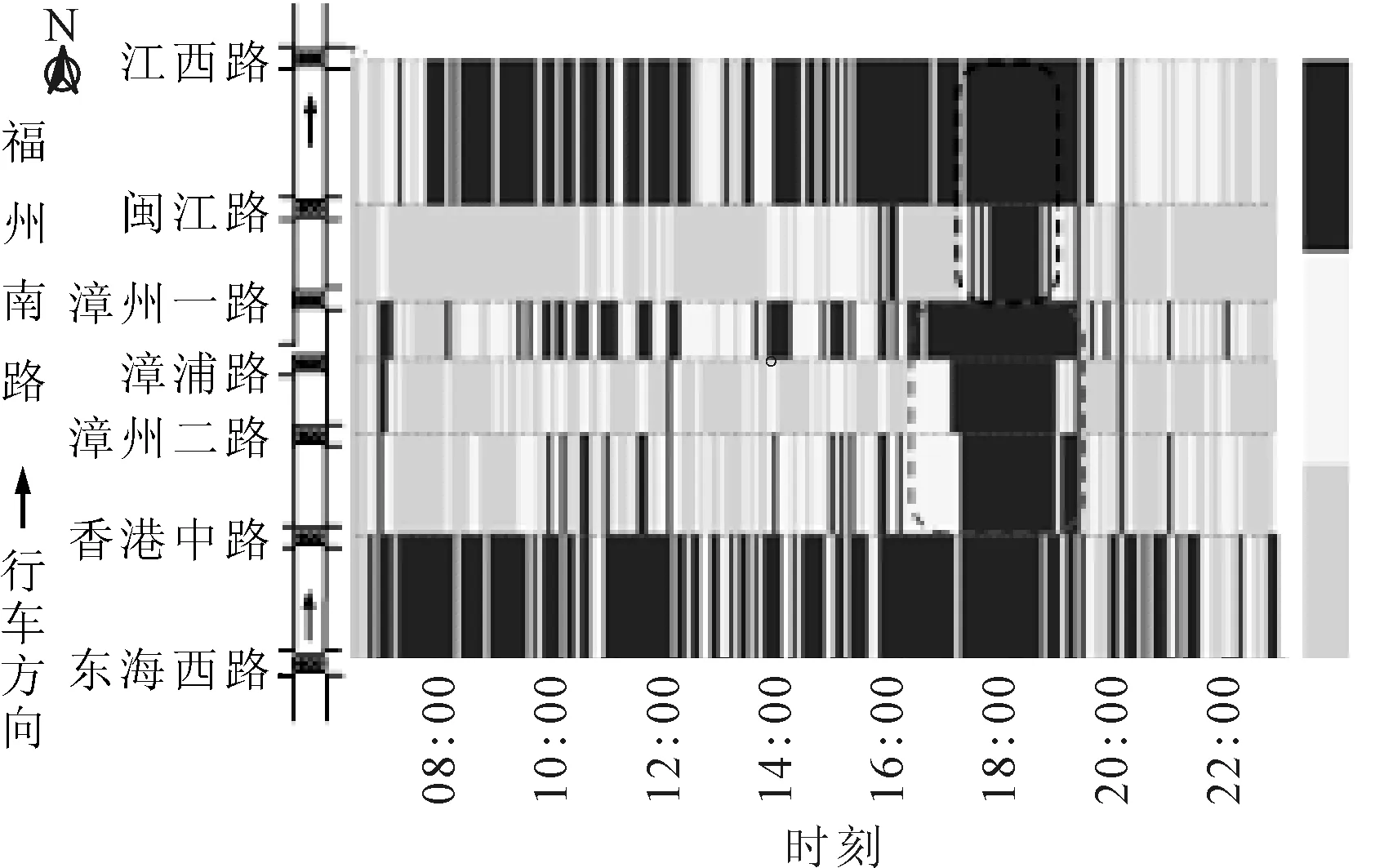
图2 研究城市主干道交通拥堵时空图
为了评价拥堵关联对主干道运行可靠性的影响,本文基于蒙特卡洛仿真建立了主干道行程时间可靠性模型,模型的关键是拥堵关联判别和不同交通状态下的行程时间分布统计.
2 考虑拥堵关联的主干道行程时间可靠性模型
2.1 路段拥堵关联建模
拥堵关联建模的关键是根据主干道各路段间拥堵状态的时空关系,对拥堵模式的进一步识别,本文采用自发性拥堵和诱发性拥堵命名规则,将由于路段拥堵关联造成的拥堵称为诱发性拥堵.
城市主干道由于受信号配时、相交道路流入车辆等因素影响,拥堵时空特征较为复杂,交通状态在拥堵与不拥堵状态间频繁转变[7].为此,本文建立了一种网格搜索算法,即针对路段每个统计间隔的交通状态,分别以排队波和消散波波速向下游路段搜索,当下游路段拥堵发生和结束时刻都在交通波影响范围内,则判断为诱发性拥堵,最终建立拥堵关联矩阵.
假设研究主干道共有n个路段,从下游至上游路段依次编号为d1,d2,…,dn.依次从第1个路段到第n路段的起始研究时刻ts至研究结束时刻te筛选拥堵状态,如第a个路段在第k个统计间隔对应的起始时刻tk发生拥堵时:若a=1,即d1发生拥堵,直接归为自发性拥堵;若a≠1,判断流程见图3.
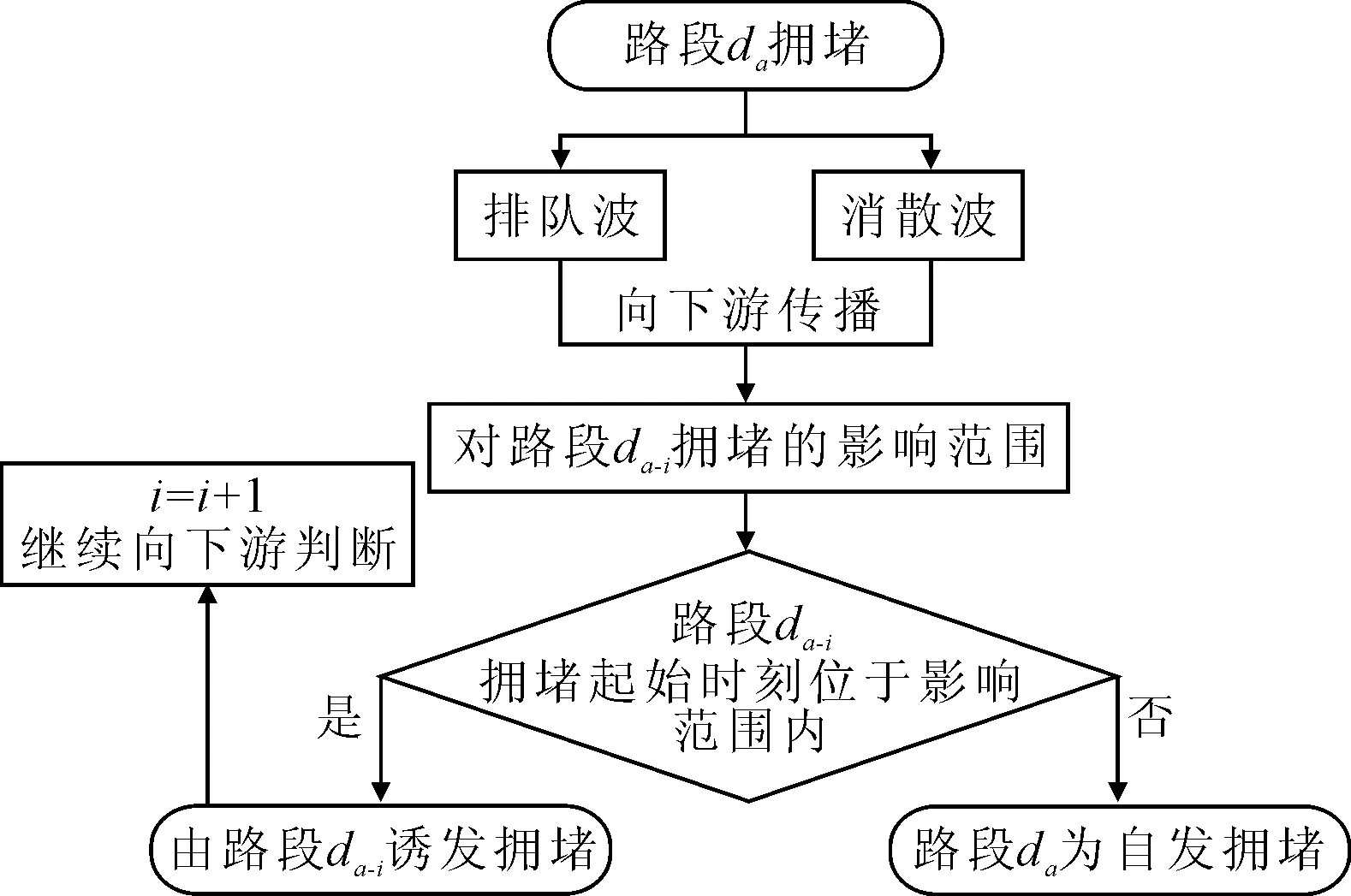
图3 拥堵关联判别流程
2.2 主干道行程时间可靠性建模
根据拥堵关联模型得到的各路段不同交通状态发生概率,可得主干道交通状态的联合概率为
Pr(S1=i11,S2=i22,…,Sj=ijj)=
πipi11pi22…pijj
(1)
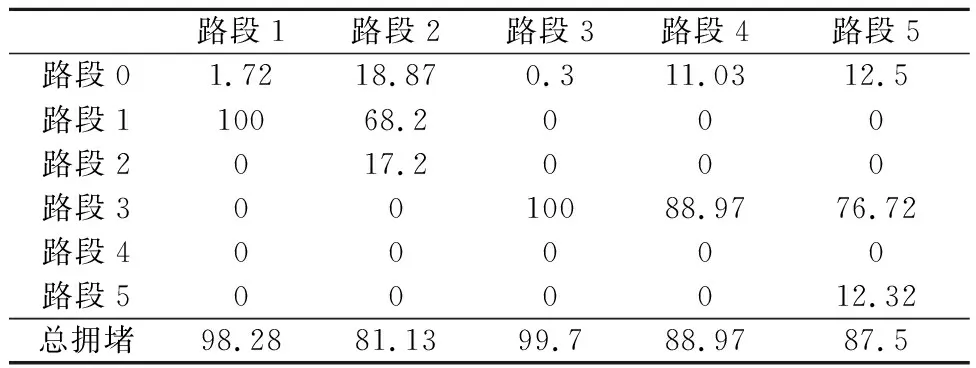
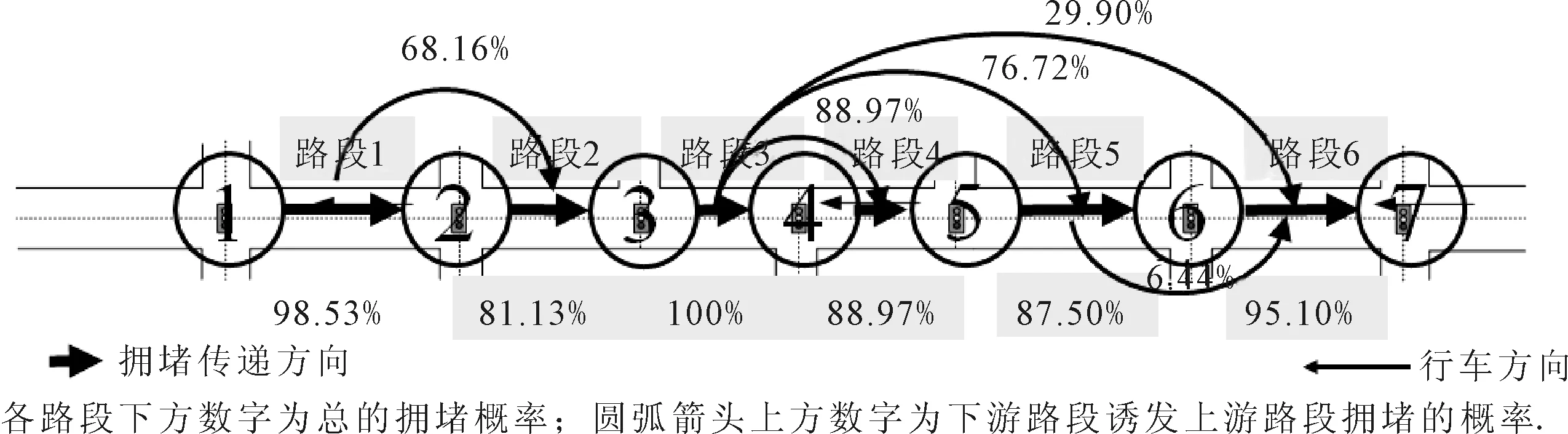
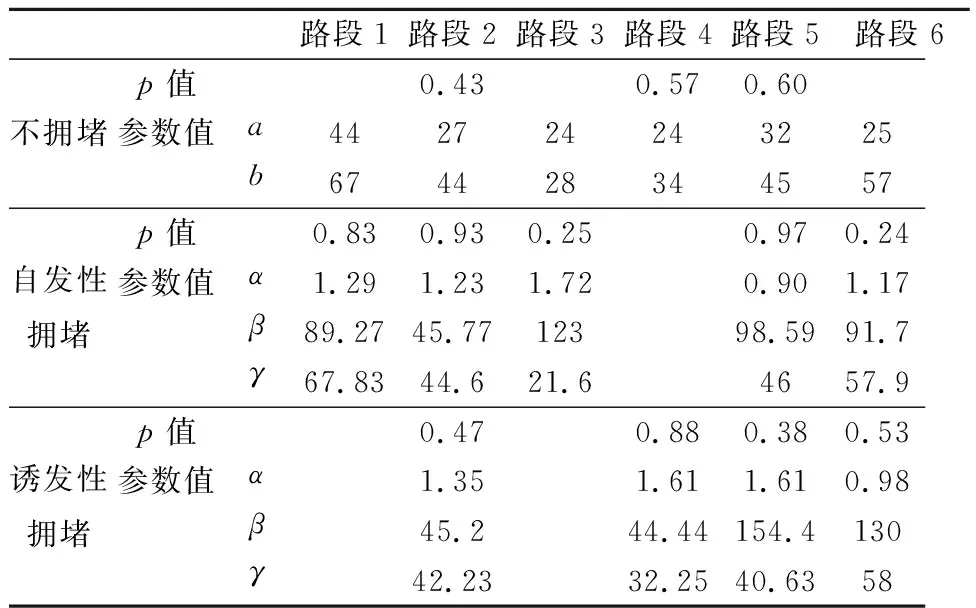
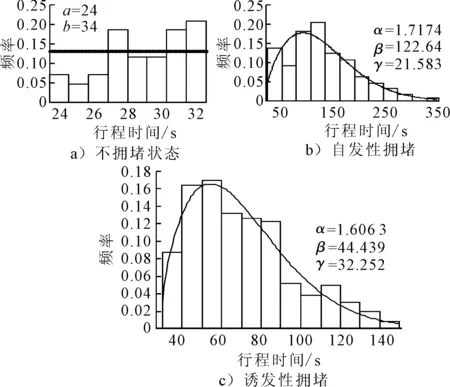
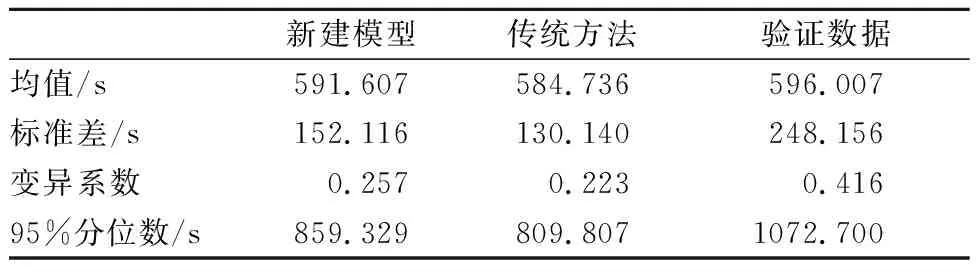
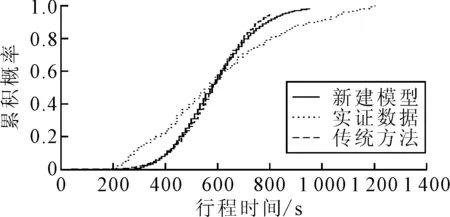
式中:Sj为路段j出现ijj状态;ij为路段编号,ij∈[0,j],当ij=0时代表不拥堵,当ij 此时,主干道行程时间为所有路段对应状态下的行程时间分布随机取值之和,计算公式可表达为 TT(S1=i11,S2=i22,…,Sj=ijj)= TTi11(i11)+TTi22(i22)+…+TTijj(ijj) (2) 式中:TTijj(ijj)为路段j在交通状态ijj时对应的行程时间分布取值. 对n次观测中每次主干道交通状态联合概率Pr(S1=i11,S2=i22,…,Sj=ijj)与对应的主干道行程时间取值TT(S1=i11,S2=i22,…,Sj=ijj)进行统计,即为最终的主干道行程时间概率特征: TT(S1=i11,S2=i22,…,Sj=ijj) (3) 为了模拟以上的主干道行程时间可靠性模型,本文提出了一个先后产生关联交通状态随机数与行程时间随机数的双层蒙特卡洛仿真模型.建模流程见图4. 图4 蒙特卡洛仿真建模流程 首先需要对提出的路段拥堵关联模型进行标定,标定的参数为排队集结波波速w1与消散波速w2,参考文献[8]并结合仿真数据验证,将w1设置为4.8 km/h,将w2设置为25 km/h,得到实证主干道路段间的拥堵关联概率,见图5.以路段2为例,晚高峰时段不发生拥堵的概率为18.87%,自发性拥堵概率为12.97%,诱发性拥堵的概率为68.16%. 实证城市主干道各路段交通状态概率矩阵可进一步整理见表1. 表1 对象城市主干道交通状态概率矩阵 % 注:路段0对应单元格行-不拥堵的概率;行列的路段编号相同单元格-自发性拥堵概率;行编号小于列编号的单元格中-诱发性拥堵概率. 图5 对象城市主干道拥堵关联概率 由此可知,城市主干道路段间拥堵关联普遍存在,福州南路可划分为三个拥堵关联区,路段1、路段3和路段6是拥堵源. 传统的路段行程时间可靠性研究中,一般认为同一时段行程时间符合单一分布特征.但由于交通状况的复杂性,在畅通与拥堵情况下行程时间有实质的不同[9-10].所以,有必要在区分交通状态的情况下对路段行程时间分布进行研究. 针对实证主干道晚高峰不同交通状态的行程时间特征统计见表2.由表2可知,自发性拥堵状态下的行程时间均值明显的大于不拥堵状态,而诱发性拥堵比自发性拥堵略高.可靠性指标[11](包括表中的标准差、变异系数、95%位行程时间)显示了相同规律. 注:样本量小于25个时,不做统计;路段6的诱发性拥堵包括多个路段. 对各路段不同交通状态的行程时间进行分布拟合,对比均匀分布(uniform distribution)、Normal分布、Lognormal分布、Three-Parameter Weibull分布和Three-Parameter Burr分布,采用K-S检验对拟合优度进行检验,显著性水平α取0.05. 1) 不拥堵状态 此时,均匀分布有更好的拟合优度,这可能与晚高峰不拥堵样本数较少且同时段交通状态较为一致有关.路段行程时间tt~U(a,b)的概率密度函数为 ,a (4) 式中:a为下边界参数;b为上边界参数. 2) 自发性拥堵状态 此时,Three-Parameter Weibull分布有更好的拟合优度.路段行程时间tt~W(α,β,γ)的概率密度函数为 × (5) 式中:α为形状参数;β为尺度参数;γ为位置参数. 3) 诱发性拥堵状态 对于诱发性拥堵情况,Three-Parameter Weibull分布拟合结果最优.概率密度函数如见式(5). 表3为不同交通状态下行程时间分布拟合优度检验的p值和各概率密度函数的参数值. 表3 行程时间分布拟合优度检验与分布参数值 图6以路段3和路段4为例展示了不同状态下的行程时间分布特征. 图6 不同交通状态下的行程时间分布 基于上文提出的主干道行程时间可靠性模型,本文通过Matlab编写蒙特卡洛仿真程序,仿真次数n设定为10 000.首先根据表1交通状态概率矩阵产生各路段代表不同交通状态的随机数,然后根据表3的行程时间概率密度函数产生行程时间随机数.由于Weibull分布为连续分布,在MATLAB产生行程时间随机数时,可能产生极小或者极大的行程时间,为此需针对这些异常数据进行检验与修正.最后,将各路段产生的行程时间求和,最终得到10 000个主干道行程时间随机值. 以香港中路—福州南路和江西路—福州南路两个交叉口位置的卡口电警匹配车辆的行程时间作为主干道的实际行程时间(样本数408个),对本文提出的行程时间可靠性模型进行验证.此外与假设各路段行程时间服从相互独立的正态分布的传统方法进行对比.结果见表4. 表4 主干道行程时间可靠性模型结果对比 由表4可知,本文提出的行程时间可靠性模型与传统方法的均值相对于验证数据无太大差异,而对于标准差来说模拟算法明显高于传统方法,这是由于传统方法认为主干道的各路段间是相互独立而高估了主干道行程时间的可靠性. 对于新建模型与验证数据的行程时间累积分布差异见图7,新建模型中行程时间出现较小值和较大值的概率要小于实证情况,这可能是由于各路段行程时间卷积求和时行程时间分布的尖峰特征被保留,而实证数据由于受到出入口、车辆变道等其他随机因素的影响,表现出更大的离散程度.而传统方法由于没有考虑拥堵关联特征,相较于新建模型产生较大行程时间的概率更低. 图7 不同模型的行程时间累积曲线对比 基于上文结果,分别从交通状态比例和不同行程时间分布类型对新建模型进行敏感性分析.结果表明:不同的交通状态概率会对主干道行程时间造成影响,随着诱发性拥堵和自发性拥堵概率的增加,主干道行程时间也会随之增加;对于行程时间分布类型,各路段的行程时间对分布类型较为敏感,其中Weibull分布拟合结果最好,正态分布拟合结果最差.但主干道行程时间可靠性对不同交通状态下的行程时间分布类型并不敏感,得到的主干道行程时间可靠性指标较为接近,这可能是在将各路段行程时间随机值卷积求和时此消彼长造成的. 本文立足于主干道路段交通状态频繁转变的特点,基于交通波理论,通过网格搜索算法,建立了拥堵关联判别模型;随后,以拥堵关联概率作为路段间行程时间相关性的衡量指标,结合不同交通状态下的行程时间分布特征,通过双层蒙特卡洛仿真建立了行程时间可靠性模型.并通过实证主干道数据对模型进行了验证,结果表明,相对于假设各路段行程时间服从相互独立的正态分布,考虑拥堵关联的主干道行程时间可靠性模型有更高的行程时间分布拟合精度与可靠性评价. 然而,本研究仍有部分不足有待进一步完善.例如,进一步提高行程时间可靠性模型精度和鲁棒性;将提出的模型拓展到实时在线层面,并增加预测功能;从交通流解析方法的角度对主干道行程时间可靠性受不同交通状态与路段间相关性的影响进行研究等.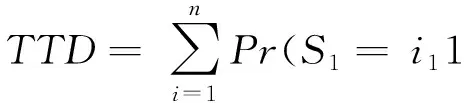

3 模型实证与分析
3.1 路段拥堵关联分析
3.2 路段行程时间分布特征分析

3.3 主干道行程时间可靠性分析
4 结 束 语
