渤海域桥梁斜体宽承台冰荷载计算*

吴甜宇 邱文亮

(大连理工大学土木工程学院 大连 116024)

0 引 言

在寒区的海洋资源开发以及港口建设中，冰荷载是海上结构物的主要控制荷载[1].

海冰是渤海有别于我国其他海域的突出问题，是该海域严重的自然灾害，对海洋结构的安全具有极大的威胁[2].渤海每年冬季都有海冰生成，它影响着渤海海上交通、渔业生产、油气开发等海上事业的运营[3].

斜体结构作为一种广泛应用于寒区海域的抗冰结构形式[4]，由于冰与斜体结构相互作用过程中能引起冰的弯曲破坏，相比其他破坏模式而言，可以有效的降低冰荷载的作用.加拿大联邦大桥[5]在设计过程中将冰荷载作为控制荷载进行考虑，并采用锥体桥墩的抗冰措施来减小冰荷载的作用.经过多年实测，锥体的设置有效的降低了冰荷载的极值，且远小于设计荷载.波斯尼亚湾的Kemi-I灯塔[6]也同样在水面线处设置了斜体破冰结构；我国渤海JZ9-3与JZ20-2采油平台[7]均采用窄锥结构作为有效的抗冰减灾措施.为了对渤海域跨海桥梁斜体宽承台进行冰荷载研究，本文针对四种规范中的计算方法开展渤海海域环境条件下不同参数对冰荷载的影响情况，采用作图分析，对斜体结构上的冰荷载进行讨论.

1 冰与斜体宽结构作用机理

斜体结构的优点在于冰体与结构相互作用过程中会引起冰体的弯曲破坏，显然，相比冰体的挤压破坏，结构承受的冰荷载要低得多.抗冰结构中斜坡角的设置可以明显使结构所受的冰荷载减小，特别是对于相对薄的海冰.但是海冰在倾斜结构表面不断攀升的过程中有可能导致结构表面设施的损坏，另外，还会增加结构的竖向荷载，这可能对恶劣土壤条件下的结构设计不利[8].

Croasdale[9]提出了一个冰与斜体结构相互作用的二维分析模型.尽管只是二维力学分析模型，但此模型对于宽体斜坡结构冰荷载的计算是合理的.然而，此模型却不适用于窄体结构，它对于窄结构而言低估了冰体的破碎荷载.其原因在于海冰与窄坡面结构相互作用过程具有三维效应，海冰的破坏区域相比结构的宽度要大得多，不是所有破碎冰体都将在斜体面上进行爬升，一些冰体会自然的从结构表面清除，此时应该应用三维弯曲失效模型进行分析.

当冰体接近一个具有倾斜面的结构时，在第一次接触时冰体开始在界面处发生弯折.随着驱动力的增加，冰体继续破坏，作用力增大.作用于结构表面的总冰力可以分解为竖向和横向两个分力，竖向分力使得冰体发生弯曲变形，当竖向分力增加到一定程度时，冰体将发生弯曲破坏.当冰体局部破坏后，断裂的冰体会被临近的冰体挤压，开始沿结构斜坡面进行爬升，进而发生回转跌落.由于需要额外的力来推动冰体攀升，这个过程中会产生更大的相互作用力，海冰与斜体结构相互作用的整个进程，见图1.

图1 冰与斜体结构相互作用进程

另外，在冰与斜体结构相互作用的过程中，存在一些附加条件.当冰与斜体结构发生接触后，斜体面结构需要具备有效的清理海冰的能力.若发生海冰附着于结构表面、海冰在结构面发生了堆积现象、或是结构被海冰包围而无法清除，就会导致斜体面结构的所有优势全部失效.在以上的情况之下，斜体面结构会表现出与直立面结构相同的破冰机理，见图2.

图2 冰与斜体结构发生堵塞现象

文中主要讨论平整冰与斜体宽结构的弯曲破坏力与爬升力，假定斜体的破冰效果良好，不会发生冰体堵塞现象.所以在此不针对冰体在斜体结构上的堆积作用进行深入探讨.

2 各国规范斜体结构冰荷载计算方法

2.1 中国JTG D60规范

文献[10]关于弯曲冰荷载的计算方法，规定当流冰范围内有倾斜表面时，冰压力应分解为横向分力FH和竖向分力FV，斜体结构上的冰荷载推荐计算公式为

FH=m0Ctσfh2tanα

(1)

FV=FH/tanα

(2)

式中：m0为冰力系数，取0.2D/h，但不小于1；D为结构斜面宽度，m；Ct为冰温系数；h为冰厚，m；σf为海冰弯曲强度，kPa；α为斜面与水平面夹角，(°).

2.2 中国Q/HSn规范

文献[11]关于弯曲冰荷载的计算方法，规定冰与斜体海洋结构相互作用的横向荷载FH与竖向荷载FV的推荐计算公式为

FH=Knh2σftanα

(3)

FV=Knh2σf

(4)

式中：Kn为冰力系数，取0.1D,D为结构斜面宽度，m；h为冰厚，m；σf为海冰弯曲强度，kPa；α为斜面与水平面夹角，(°).

2.3 俄罗斯SNIP规范

文献[12]关于弯曲冰荷载的计算方法中规定冰与斜体结构相互作用的横向荷载FH与竖向荷载FV的推荐计算公式为

FH=0.1σfDhtanα

(5)

FV=FHcotα=0.1σfDh

(6)

式中：D为结构斜面宽度，m；h为冰厚，m；σf为海冰弯曲强度，kPa；α为斜面与水平面夹角，(°).

2.4 加拿大CSA规范

文献[13]对于斜体结构冰荷载的计算采用冰与斜体结构相互作用的二维力学分析模型，见图3.

图3 冰与斜体结构相互作用二维力学模型

冰与斜体结构相互作用力的横向分量FH与竖向分量FV，可以写为

FH=FNsinα+μFNcosα

(7)

FV=FNcosα-μFNsinα

(8)

FH=FVC

(9)

文献[9]认为当冰体的弯曲强度与其初始弯曲破坏所需的竖向力相等时，那么结构单位宽度上的竖向力与横向力，可以写为

FV/D=0.68σf(ρwgh5/E)0.25

(10)

FH/D=0.68σf(ρwgh5/E)0.25C

(11)

式中:D为结构斜面宽度,m；h为冰厚，m；σf为海冰弯曲强度，kPa；ρwg为水的重力密度，N/m3；E为海冰的弹性模量，GPa.

Croasdale二维力学模型充分考虑了冰体在弯曲破坏后沿宽体斜坡的爬升作用，断裂冰体在结构的斜面上还会被提升至一定的高度，随后回转跌落.冰体在斜面上被推升的垂直距离为Z，平行于斜体面的作用力FC可以写为

ρig(sinα+μcosα)

(12)

式中：ρig为冰的重力密度，N/m3.

冰体弯曲破坏与爬升的横向合力FH写为

(13)

综上，作用在斜体结构单位宽度上的水平总力可以写为

FH/D=C1σf(ρwgh5/E)0.25+zhρigC2

(14)

式中：系数C1与C2只与斜面角度α与摩擦系数μ相关，可以写为

3 渤海域斜体结构冰荷载计算参数影响分析

参考文献[11]，得到了渤海海冰的力学性能参数，并对结构计算参数进行了相关假定，见表1.

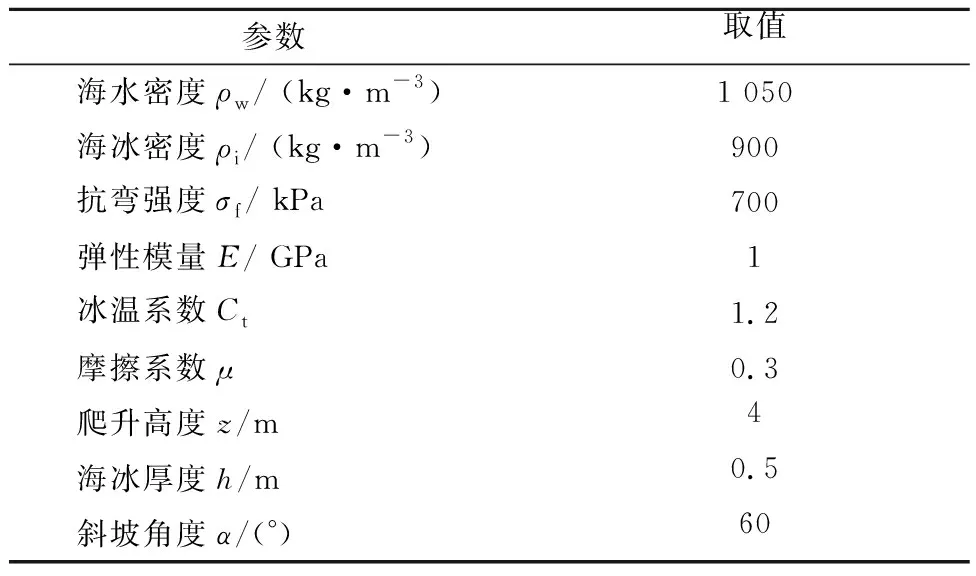
表1 计算参数

寒区结冰海域环境条件下，冰与斜体结构相互作用过程中，海冰对斜体结构起破坏作用的主要是冰荷载的横向分力，所以在结构的抗冰设计过程中应当对横向冰荷载进行重点关注.

图4为各规范下结构的不同斜坡角度对横向冰荷载的影响效应.由图4可知，由于JTG D60，Q/HSn与SNIP规范均未考虑冰体沿斜体坡面的爬升作用，只给出了横向与竖向的破坏荷载.然而，CSA规范给出了冰体爬升过程中任意高度处的横向冰力，其中包括弯折力与爬升力两部分组成.随着结构斜坡角度的增大，横向冰荷载均呈现增长的趋势，但规范Q/HSn与规范SNIP计算所得的荷载水平较低.其中根据规范SNIP计算，斜坡角度由20°增大到65°，横向冰荷载由13 kN/m增大到75.5 kN/m.规范JTG D60与规范CSA计算所得的冰荷载水平较高，且随着斜坡角度的增加，横向荷载的增长趋势十分明显.对于规范CSA而言，当斜坡角度大于45°时，横向力对坡角的增大非常敏感，呈现了陡增的变化趋势.横向力也由20°坡角的47.9 kN/m增大到65°坡角的215.4 kN/m.可以观察到，斜坡角度在30°～60°范围内由规范JTG D60计算所得的横向冰荷载要高于规范CSA的计算值，并远大于其他两个规范的计算值.由此可见，规范JTG D60在未考虑冰体爬升作用下的横向荷载值偏大，侧面说明了规范中给出的冰荷载的计算公式过于保守.

图4 各规范下不同斜坡角横向冰力

图5为各规范下不同冰厚对横向冰荷载的影响效应.由图5可知，随着冰厚的增加，各规范的计算冰荷载值均呈现增长的趋势.在冰厚小于0.5 m下，根据规范Q/HSn计算得出的荷载值明显低于其他规范的计算值.对于规范CSA计算的横向总荷载而言，弯折力相对较小，爬升力占了主要的部分.对于宽结构的冰荷载计算，考虑爬升力的作用是合理、准确的.

图5 各规范下不同冰厚横向冰力

图6为CSA规范下不同摩擦系数与不同爬升高度对横向冰荷载的影响效应.由图6a)可知，随着斜坡角度的增大，横向冰力呈现指数增长趋势，冰与结构的摩擦系数越大，横向冰力也随之增大，即使在小坡角的情况下，荷载量值的变化也较为明显.可见，在冰荷载的计算中，应当合理的选取冰与结构的摩擦系数.

由图6b)可知，随着冰厚的增大，横向冰力呈现线性增长趋势，冰体的爬升高度越大，横向冰力也随之增大.在冰厚为1 m的情况下，爬升高度由1 m增大到5 m，横向冰力由138 kN/m增大到311 kN/m.

因此，在冰荷载的计算中，首先应当确定冰体在斜体结构上最大的爬升高度，准确合理的确定冰体爬升的最大高度是得到横向冰荷载的前提条件.

图6 CSA规范下不同摩擦系数与不同爬升高度横向冰力

4 渤海域桥梁斜体宽承台冰荷载计算

拟建的“秦—大”跨海通道工程跨越渤海，连接辽宁省大连市与河北省秦皇岛市，跨海部分均采用桥梁工程，海上工程长约144 km.由于桥址所在海域多为20～30 m的深水区域，故采用高桩承台群桩基础结构形式.非通航孔桥梁的典型承台平面尺寸为21 m×13 m，考虑到本海域桥梁冰荷载问题，设计水面线位于承台中部，承台采用斜坡面的迎冰形式.

利用规范CSA进行桥梁承台的冰荷载计算，选取海冰的爬升高度为5 m，海冰弯曲强度为700 kPa，冰与结构的摩擦系数为0.3，在四种斜坡角度，1 m冰厚范围内，计算承台冰荷载并绘制出承台单位宽度横向冰荷载曲线，见图7.

图7 CSA规范下不同斜坡角横向冰力

由图7可知，斜体面宽承台结构与冰体相互作用的进程中，冰体所需的弯曲折断力明显小于冰体在斜体面上攀升所需的爬升力.针对假定的爬升最大高度5 m而言，各斜体设置角度下冰体所需的折断力近似为爬升力的1/3，说明斜体面宽结构与冰体作用过程中爬升力相比折断力占据主导地位.

对比图7中的a)～d)可知，不同斜体设置角度下横向冰荷载均随着冰厚的增加而增大，且增长趋势基本相似.当冰厚为0.5 m时，斜坡角为45°，50°，55°，60°的桥梁承台(迎冰面21 m)横向冰荷载分别为1 659，1 932，2 394，3 192 kN.

综上，在进行桥梁斜体宽承台的抗冰设计过程中，应当充分考虑设置角度、摩擦系数等结构因素的影响，应当合理的考虑施工难度、工程造价及结构合理性等综合因素.

5 结 论

1) 对于宽结构而言，利用二维力学分析模型考虑冰体的爬升作用是合理、准确的.但对于窄结构而言，冰的清理机制或许取代了冰体的攀升作用，利用冰体的爬升公式计算的荷载值是偏高的，此时应采用三维模型进行计算.

2) 随着冰厚、斜坡角度的增大，横向冰荷载均呈现增长的趋势.由于只考虑了冰体的弯曲破坏力，根据规范Q/HSn与规范SNIP计算所得的冰荷载水平略低.

3) 规范CSA利用二维力学分析模型，充分考虑了冰体在结构表面的爬升作用，计算所得的荷载值也明显高于规范Q/HSn与规范SNIP，但规范JTG D60在未考虑冰体爬升作用的情况下荷载值偏大，说明其计算公式过于保守.

4) 桥梁斜体宽承台的抗冰设计过程中，应当充分考虑斜坡面设置角度、摩擦系数等结构因素的影响，合理降低极值冰荷载，综合考虑施工难度、工程造价等因素.