垂直循环式立体车库液压控制系统的特性分析

张启辉，苏东海

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

0 引言

立体车库传统的驱动方式是电机驱动，而电机启动电流大、负载变化频繁、不易精确控制。本文以PCX16DX.YD.YL型立体车库为研究对象,以液压系统作为驱动系统为垂直循环升降平台的运动提供动力。液压系统具有无极调速、功率高、响应快、抗干扰能力强等优点，采用液压系统驱动能够提高整个装置的稳定性、缓冲特性、使用寿命等。而阀控液压马达运动特性的好坏直接影响立体车库的工作效率等，所以本文采用MATLAB/Simulink对液压系统进行仿真分析，对阀控马达的特性进行研究。

1 PCX16DX.YD.YL型立体车库阀控液压马达系统理论分析

1.1 车库驱动系统的组成及工作原理

图1为PCX16DX.YD.YL型立体车库液压驱动系统原理图，采用液压驱动系统克服了由电机直接驱动带来的启动制动过程中的冲击震荡等缺点。其工作原理为：首先柱塞泵5从液压油箱1中经过过滤器2过滤吸取液压油，通过换向阀7流向液压马达。换向阀7左位工作时，液压油首先通过梭阀8打开制动器11，液压马达开始正向转动，带动车库回转系统正向转动；同理，换向阀右位工作时液压马达反转；换向阀中位工作时制动器11抱紧液压马达,马达停止转动。液压马达通过啮合齿轮连接立体车库回转链轮，链条带动轿厢完成垂直循环运动。因为立体车库频繁的启动、制动以及反向运动，液压马达和回转机构会因为惯性的原因产生冲击震动，这样会导致一侧压力升高，压力升高到缓冲阀组9的临界压力时，阀组中的溢流阀被打开，高压侧液压油就进入低压侧，减小了系统的压力冲击，提高了系统的稳定性。液压系统制动时，制动器11的泄油需要经过节流阀的限速作用保证回转平台完全制动后机械锁紧，这种延时抱闸的制动器又称为非工作性制动器，而车库的稳定运行主要取决于阀控液压马达的运动特性，后文主要针对马达的运动特性进行分析。

1-油箱；2-进油过滤器；3-回油过滤器；4-电机；5-柱塞泵；6-溢流阀；7-三位四通电磁换向阀；8-梭阀；9-缓冲阀组；10-双向液压马达；11-制动器

1.2 液压马达基本方程

伺服阀的线性化流量方程为：

QL=KqXV-KcPL.

(1)

其中：XV为伺服阀阀芯位移；Kc为流量-压力系数；Kq为流量增益；PL为负载压降。

液压马达的流量连续性方程为：

(2)

其中：Dm为液压马达排量；θm为液压马达转角；Ctm为总泄漏系数；Vt为液体总压缩系数；βe为液体等效体积弹性模量。

液压马达和负载的力矩平衡方程为：

PLDm=Jts2θm+Bmsθm+Gθm+TL.

(3)

其中：Jt为负载转动惯量；Bm为黏性阻尼系数；G为负载的扭矩弹簧刚度；TL为外负载力矩。

式(1)、式(2)和式(3)是阀控液压马达的三个基本方程，它们完全描述了阀控液压马达的动态特性。消去中间变量QL和PL就可以求得阀控液压马达在阀芯位移XV和外负载力矩TL同时输入时的总输出为:

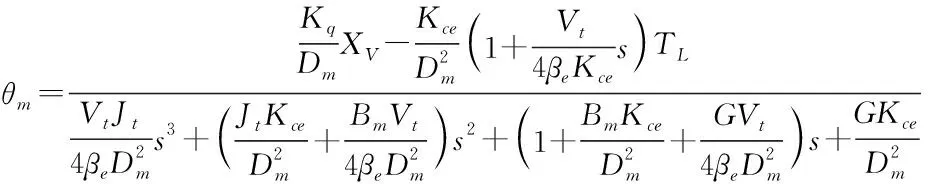
(4)

(5)

其中：ωh为液压的固有频率；ζh为液压阻尼比，且有

(6)

(7)

通常负载黏性阻尼系数Bm很小，所以式(7)可以写成:

(8)

液压马达轴的转角对阀芯位移的传递函数为：

(9)

液压马达轴的转角对外负载力矩的传递函数为：

(10)

2 基于Simulink阀控液压马达系统的特性分析

通过上述理论分析得到的结论是：阀控液压马达特性受阀的开口位移XV、负载转矩TL、马达排量Dm、转动惯量Jt、液体等效体积弹性模量βe、液压马达两个容腔及连接管道的液体总压缩系数Vt和总流量-压力系数Kce的影响。其中马达排量Dm事先选定，βe、Vt、Kce都确定，所以本文以负载转矩、转动惯量和速度放大系数为研究对象，而由液压阻尼比公式(8)得出转动惯量和液压阻尼比的平方呈线性关系，所以本文只对负载转矩、液压阻尼比和速度放大系数进行仿真。

系统参数为：反馈增益Kf=163；反馈调节系数Ke=0.006；比例阀的放大增益Ka=0.12；液体等效体积弹性模量βe=7×108Pa；液压马达两个容腔及连接管道的总容积系数为3×10-4m3/s；液压马达排量Dm=27.4 m3/rad；Jt=0.35 kg·m2；由固有频率公式计算ωh=65.51 rad/s；流量—压力系数Kce=Kc+Ctm,Kc=1.5×10-6m3/s；Ctm=0.5×10-6m3/s，所以Kce=2×10-6m3/s。

将已知参数代入式(5)可以得到阀控液压马达的传递函数为：

(11)

应用MATLAB/Simulink建立阀控液压马达控制系统的线性数学模型的仿真框图，如图2所示。

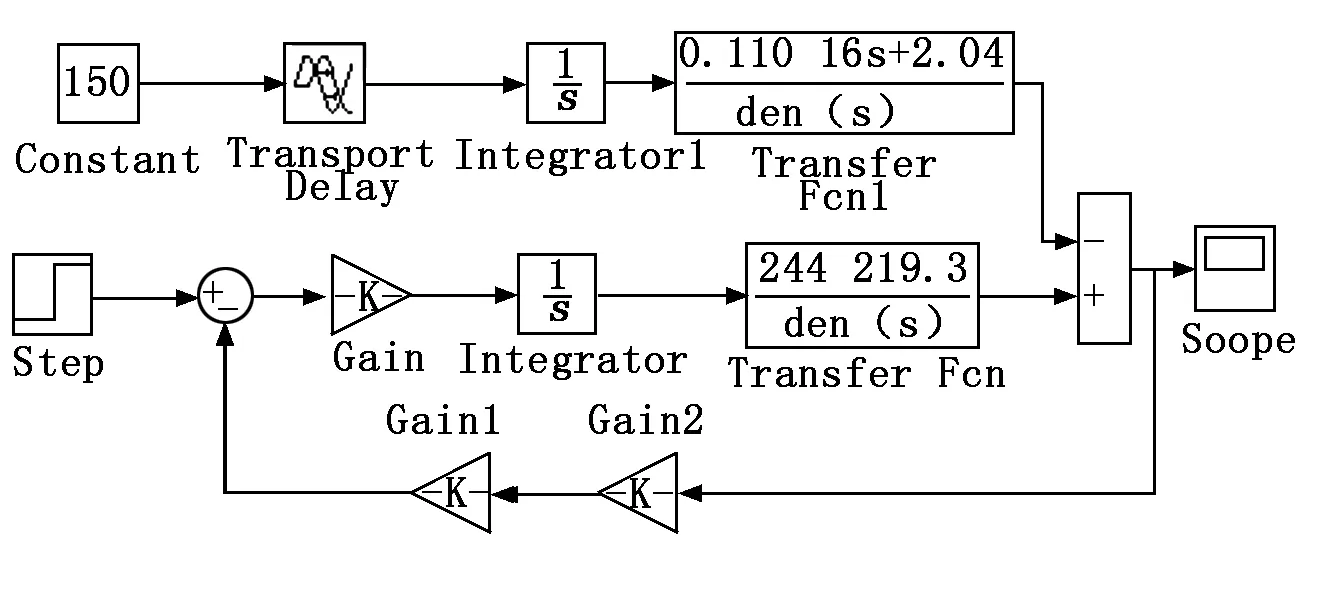
图2 阀控马达系统的建模仿真图

2.1 不同工况负载下系统的响应

如图2所示，阀控马达仿真图中的Transport Delay设置延迟加入负载，仿真时间设置为70 s,延迟时间设置为40 s，分别加入负载力矩为0 Nm、150 Nm和300 Nm，观察仿真结果如图3所示。由图3可知，该阀控液压马达能够在较短的时间内达到要求的数值，响应速度较快,上升时间较短，最大超调量较小，可满足车库的要求。当加入外负载时系统的稳定性明显被打破，但很快系统又恢复稳定运行，随着负载的增加马达的转速减小，有助于系统的稳定运行和控制，达到无极调速的效果。

2.2 液压阻尼比对系统性能的影响

系统的液压阻尼比ζh和固有频率ωh是影响该阀控液压马达系统的两个重要参数。要改变系统的固有频率比较困难,而调节系统的液压阻尼比则要容易很多,只要调节液压马达两个容腔之间的阻尼孔的大小、改变马达的内泄漏量即可。在相同的输入信号下，改变系统的液压阻尼比得到的不同仿真结果如图4和图5所示。

图3不同负载下系统的响应图4阻尼系数为0.8和0.2时马达轴转角仿真图形图5阻尼系数为0.1时马达轴转角仿真图形

如图4所示，液压马达的阻尼比为0.8时系统在0.5 s内达到稳定，当阻尼比减小到0.2时图像出现明显的波动。调整为0.1左右时仿真图如图5所示。

由以上的仿真结果可知,随着系统液压阻尼比的减小，系统响应的振荡特性表现得愈加强烈。当阻尼比在0.2～0.8范围内时，即系统处于欠阻尼状态时，振荡不太严重，而且过渡时间较短。所以在调试该阀控液压马达系统参数时应该注意尽量使系统工作在欠阻尼状态，使其具有持续时间较短的过渡过程和平稳的运行过程。

2.3 不同速度增益对系统特性的影响

速度增益表示阀对液压马达速度控制的灵敏度。速度放大系数直接影响系统的稳定性、响应速度和精度，提高速度放大系数可以提高系统的响应速度，但系统的稳定性变差，因此要合理地选择速度放大系数。本文选择三个参数k1、k2、k3(k1≥k2≥k3)进行仿真分析，结果如图6所示。当速度放大系数为k1时，系统响应速度很快，1.5 s达到稳定状态，但稳定性不好；当速度放大系数为k2时，系统3 s达到稳定状态；放大系数为k3时，系统9 s达到稳定状态，响应速度减小7.5 s，但稳定性强于前者。

3 结论

本文结合车库的具体运行特点(垂直循环运动)，分别分析了三组典型运动状态：空载运行、满载运行和极限负载运行。分析结果表明车库可以正常运行，从空载运行到有负载运行可以看出随着负载的增加，会降低马达的转速，进而提高了系统的稳定性；液压阻尼比在0.2～0.8区间时液压系统的稳定性最好，最适合车库的运行，当阻尼比低于0.2时，系统开始出现微小的振荡，稳定性变差，并随着阻尼比的减小振荡加剧；速度放大系数越大，系统响应越快，但稳定性不好，反之响应速度越慢，但稳定性越好，因此在实际中应根据系统要求选择合适的速度放大系数。

图6 不同速度放大系数对系统特性的影响