连续管复合裂纹的应力强度因子有限元分析*
2018-11-01刘少胡杨明合
管 锋,王 振,刘少胡, 杨明合
(1.长江大学 机械工程学院,湖北 荆州 434023;2.长江大学 石油工程学院,湖北 武汉 430100)
0 引言
经过50多年的发展,连续管已经应用于清蜡、酸化挤水泥、压井、冲砂洗井、负压射孔、试井测井完井、钻井等20多种作业[1]。截止到2017年年底,全球范围内的连续油管作业机共有1 955台[2]。虽然连续管的应用已趋近成熟,但连续管在作业过程中还是经常会发生低周疲劳断裂事故[3]。这是由于连续管在生产应用过程中,焊缝和缺陷部位会产生应力集中,裂纹会不可避免的出现,一旦裂纹扩展导致结构断裂,就会发生低周疲劳断裂,给连续油管作业带来巨大经济损失。相关研究表明[4],应力强度因子是评判含裂纹构件是否断裂及裂纹扩展速率的重要参量,因此,正确计算裂尖应力强度因子能够提高连续管低周疲劳断裂事故的预防能力,从而实现高效率的连续管作业。
目前,计算应力强度因子的方法有解析法[5]、边界配位法[6]、有限单元法[7]、权函数法、复变函数法[8]、扩展有限元法[9-12]等,由于有限单元法、扩展有限元法的计算结果相对精确,易于获得,所以,一般采用有限单元法、扩展有限元法计算复合裂纹的应力强度因子。而相比于有限单元法,扩展有限元法具有裂纹扩展过程中无需重新划分网格、裂尖不需要加密、使用同样的网格、不存在数据传递问题等优点[13-17]。基于这些优点,本文利用XFEM对连续管进行数值模拟研究。当前,对二维平面的Ⅰ型裂纹应力强度因子的研究很多[18],而对复杂三维模型,例如厚壁圆筒型的Ⅱ型裂纹和Ⅲ型裂纹的应力强度因子研究相对较少。本文基于ABAQUS软件平台的XFEM功能,研究了裂纹角度对CT80连续管Ⅰ型裂纹、Ⅱ型裂纹和Ⅲ型裂纹的应力强度因子的影响。
1 应力强度因子求解的基本理论与方法
根据构件的受力方式,可以将裂纹分为Ⅰ型裂纹(张开型)、Ⅱ型裂纹(滑移型)、Ⅲ型裂纹(反平面剪切型)等3种类型,如图1所示。

图1 3种类型的裂纹Fig.1 Three types of cracks
在进行裂纹分析时,应力强度因子K,J积分、能量释放率G等是断裂参量的几种重要数值计算方法,由于J积分、能量释放率G等数值计算方法相对繁琐和复杂,用来分析裂纹扩展问题并不方便;而应力强度因子理论已经相当成熟且准确。因此,本文在分析CT80连续管的裂纹扩展问题时,采用应力强度因子K的数值计算方法。可将CT80连续管的裂纹抽象为三维模型,其三维裂纹模型裂尖尖端的坐标如图2所示。
图2的三维裂纹模型中,局部直角坐标系由坐标分量X,Y,Z和O构成,XOZ为裂纹尖端的水平平面,YOZ面为切平面,XOY面为法平面;局部极坐标系由坐标分量r和θ构成,r和θ分别是极坐标下计算点的半径与角度。裂纹尖端区域应力场的位移表示如下[19]:

图2 三维裂纹前缘任意一点的坐标值及位移场Fig.2 Coordinate value and displacement field of any point at the front edge of 3D crack

(1)
式中:μ,ν,w分别对应的是裂纹尖端在X,Y,Z方向的位移,mm;r是极坐标下计算点的半径,θ是极坐标下计算点的角度,(°);G为剪切模量,MPa;KⅠ,KⅡ和KⅢ分别为Ⅰ型裂纹、Ⅱ型裂纹和Ⅲ型裂纹的应力强度因子,MPa·mm1/2;o(r)为高阶无穷小量。k的取值如式(2)所示。
(2)
当裂纹区域内的一点θ=±180°,且位移r已知时,可以得到对称裂纹的应力强度因子计算公式:
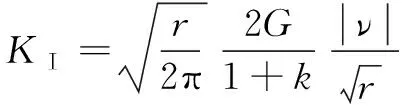
(3)
式中:K为总应力强度因子,MPa·mm1/2。
2 应力强度因子的计算
选取的模型为CT80连续管,查阅连续油管工程技术手册[20]可知其材料力学性能参数,如表1所示。CT80管的外径为38.10 mm,壁厚分别为2.77 mm,截取的长度为100 mm。
CT80连续管的网格及裂纹位置及形状如图3所示,裂纹处于模型的中心,裂纹与XOY面的夹角为0°,裂纹长度为1/12圆周,裂纹宽度分别设定为0.25,0.50,0.75,1.00,1.25,1.50和1.75 mm。对模型一端分别施加50,100,150,200,250和300 MPa的均匀拉力。

表1 常温下CT80连续管的力学性能Table 1 Mechanical properties of CT80 coiled tubing at room temperature

图3 CT80连续管有限元模型及裂纹形状 Fig.3 Finite element model and crack shape of CT80 coiled tubing
查阅应力强度因子手册[21],可以根据公式计算厚壁圆筒型模型的应力强度因子,其计算公式如下:
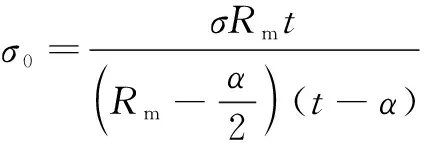
(4)
式中:σ0是裂纹面上的平均应力,MPa;σ是远处均匀拉伸应力,MPa;Rm为连续管平均半径,mm;t为连续管的壁厚,mm;α为裂纹宽度,mm;KL为应力强度因子手册得到的应力强度因子计算解,MPa.mm1/2;B为形状修正系数。
为了验证ABAQUS中裂纹扩展的准确性,计算了裂纹宽度及裂纹所受载荷变化时,裂尖应力强度因子的变化,并与应力强度因子手册得到的计算解进行比较,求出相对误差。其结果如表2-3所示。KS为利用XFEM得到的应力强度因子有限元解,MPa·mm1/2。
从表2和表3中的误差分析可以看出,利用扩展有限元法求得的应力强度因子与通过应力强度因子手册计算的结果很接近,最大相对误差为-7.12%,因此,可以认为通过扩展有限元法求得的应力强度因子是相对准确可靠的。
对单向拉伸载荷为100 MPa、裂纹宽度为0.5 mm模型的裂纹尖端受力进行分析,得到的应力云图如图4所示。裂纹扩展的20步过程中,裂纹尖端处所受到的应力始终是最大的,表明了裂尖处有很大的应力集中,这会加速CT80连续管的裂纹扩展。

表2 裂纹应力强度因子随拉伸应力的变化(α=0.5 mm)Table 2 Crack stress intensity factor changes with tensile stress(α=0.5 mm)

表3 裂纹应力强度因子随裂纹宽度的变化(σ=100 MPa)Table 3 Crack stress intensity factor changes with crack width(σ=100 MPa)

图4 不同分析步数下的CT80连续管受力云图Fig.4 Stress cloud diagram of CT80 coiled tubing under different analytical steps
3 裂纹角度对应力强度因子的影响
裂纹的角度对应力强度因子有很大影响,用解析法等方法计算复杂三维模型的复杂受力相当复杂,而利用扩展有限元法计算复杂模型的应力强度因子则较为简便准确。为了研究裂纹角度对Ⅰ型、Ⅱ型和Ⅲ型裂纹的应力强度因子KⅠ,KⅡ和KⅢ的影响情况,利用ABAQUS软件平台的扩展有限元(XFEM)技术分别计算不同裂纹角度下的KⅠ,KⅡ和KⅢ值。
首先建立不同裂纹方向CT80连续管的模型。取CT80连续管的壁厚为2.77 mm,外径为38.10 mm,长度为100 mm。对模型一端施加100 MPa的均匀拉力,力学材料参数如表1所示。裂纹的长度为1/12圆周,宽度分别为0.5,1.0和1.5 mm。裂纹方向θ(裂纹面与XOY平面的夹角)分别为0°,15°,30°,45°,60°,75°和90°。模型如图5所示。
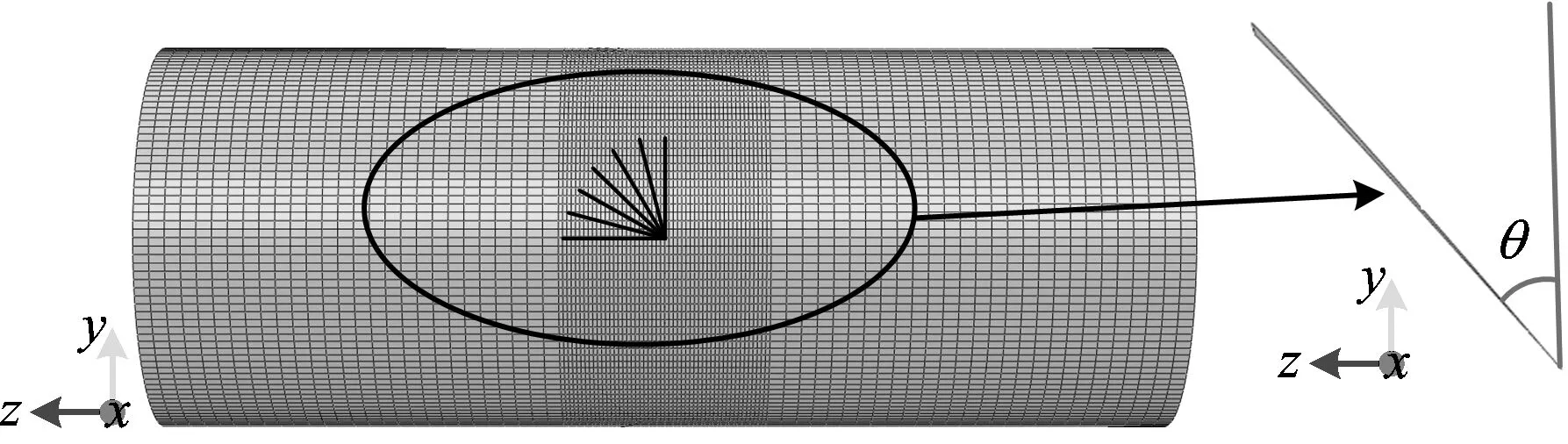
图5 不同裂纹角度θ下的CT80连续管模型Fig.5 CT80 coiled tubing model with different crack angles
3.1 裂纹角度对Ⅰ型裂纹应力强度因子KⅠ的影响
通过扩展有限元法计算可以得到不同裂纹角度对Ⅰ型裂纹应力强度因子KⅠ的影响,其结果如图6所示。
从图6可以看出,当裂纹宽度α分别为0.5,1.0,1.5 mm时,随着裂纹角度θ的增大,Ⅰ 型裂纹应力强度因子KⅠ不断减小。

图6 不同裂纹角度θ下的Ⅰ型裂纹应力强度因子KⅠFig.6 Stress intensity factorKⅠof typeⅠ cracks under different crack angles
3.2 裂纹角度对Ⅱ型裂纹应力强度因子KⅡ的影响
通过扩展有限元法计算,可以得到不同裂纹角度对Ⅱ型裂纹应力强度因子KⅡ的影响,其结果如图7所示。

图7 不同裂纹角度θ下的Ⅱ型裂纹应力强度因子KⅡFig.7 Stress intensity factorKⅡof type Ⅱ cracks under different crack anglesθ
从图7可以看出,当裂纹宽度α分别为0.5,1.0和1.5 mm时,随着裂纹角度θ的增大,Ⅱ型裂纹应力强度因子KⅡ的整体趋势是先增大后减小;但是,KⅡ值总是很小,多个值趋近于0。
3.3 裂纹角度对Ⅲ型裂纹应力强度因子KⅢ的影响
通过扩展有限元法计算可以得到不同裂纹角度对Ⅲ型裂纹应力强度因子KⅢ的影响,其结果如图8所示。

图8 不同裂纹角度θ下的Ⅲ型裂纹应力强度因子KⅢFig.8 Stress intensity factorKⅢ of type Ⅲ cracks under different crack angles θ
从图8可以看出,当裂纹宽度α分别为0.5,1.0和1.5 mm时,随着裂纹角度θ的增大,Ⅲ型裂纹应力强度因子KⅢ的整体趋势是先增大后减小,在裂纹角度θ=45°时达到最大值。
3.4 裂纹角度对总应力强度因子K的影响
由前面的表2和表3可知,利用CAE软件平台的扩展有限元法计算出的应力强度因子比较精确。由扩展有限元法计算出KⅠ,KⅡ,KⅢ值后,利用式(3)可以求得总的应力强度因子K,其计算结果如图9所示。
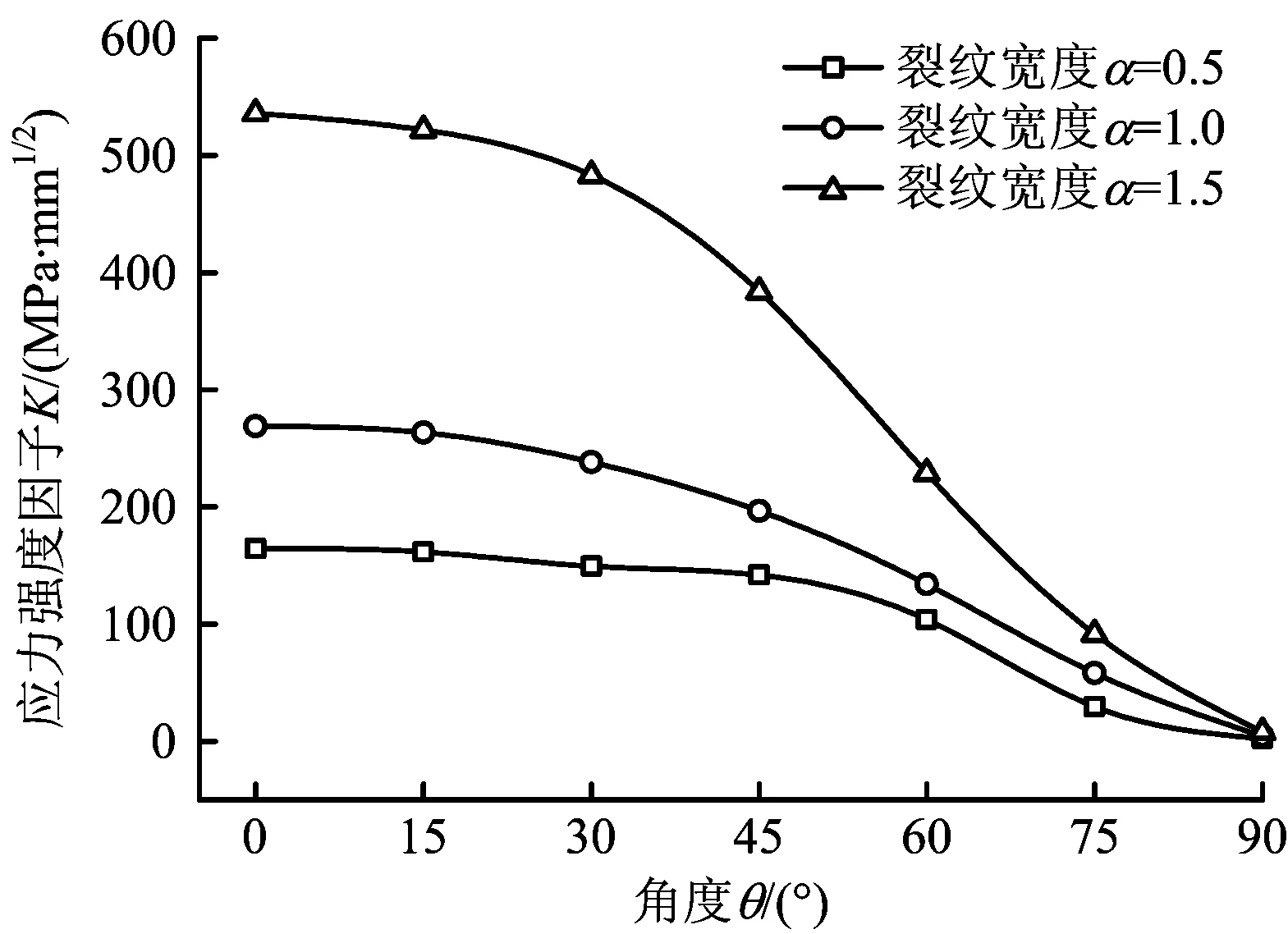
图9 不同裂纹角度θ下的总裂纹应力强度因子KFig.9 The total stress intensity factor K under different crack angles θ
从图9可以看出,当裂纹宽度α分别为0.5,1.0和1.5 mm时,随着裂纹角度θ的增大,总裂纹应力强度因子K不断减小。K与KⅠ的整体趋势大体一致,这表明在不同裂纹角度下,Ⅰ型(张开型)裂纹是最为危险的裂纹。
4 含裂纹CT80连续管安全性预测
当前对CT80连续管的无损裂纹检测方法主要有2种,对于不可见的内部裂纹,采用涡流探伤的方法检测;对于可见的开口裂纹,采用超声波检测。根据上述2种方法检测到的裂纹形状建立有限元模型,利用XFEM可以快速计算出该裂纹形状下的CT80连续管裂尖应力强度因子K。
根据20世纪60年代Irwin[21]提出的应力强度因子方法可知,控制断裂的参数是材料的断裂韧性KC。相应的断裂准则为:
K=KC
(5)
该准则提出,应力强度因子既适用于稳定裂纹扩展,也适用于疲劳和应力腐蚀的亚临界裂纹扩展。
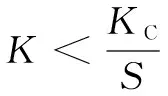
5 结论
1)利用ABAQUS软件平台的扩展有限元法(XFEM)功能,可以精确的求得裂尖应力强度因子。扩展有限元法计算出的应力强度因子与应力强度因子手册上求得的应力强度因子很接近。对于受单向拉伸载荷的CT80连续管试样,其构件受到的最大应力始终位于裂尖处。
2)随着裂纹角度θ的增大,KⅠ不断减小;KⅡ的整体趋势是先增大后减小,但是,KⅡ值总是很小,趋近于零;KⅢ的整体趋势是先增大后减小;在裂纹角度θ为45°时达到最大值;总裂纹应力强度因子K不断减小;K与KⅠ的整体趋势大体一致,这表明在不同裂纹角度下,Ⅰ型(张开型)裂纹是最为危险的裂纹。
3)通过比较ABAQUS软件计算出的应力强度因子与CT80连续管的材料断裂韧性KC,可有效判断构件是否处于安全状态。
