基于灾变的人群疏散避灾路径优化及应用*

陈一洲，尹浩东，孙 旋，晏 风，王大鹏

(1.中国建筑科学研究院有限公司，北京 100013；2.北京交通大学轨道交通控制与安全国家重点实验室，北京 100044)

0 引言

随着我国城市化的快速发展，城市交通拥堵情况也越来越频繁，其导致的安全性及应急管理问题越来越受到人们的普遍关注[1-4]。近年来，各类突发事件频繁发生，如“12·31上海外滩踩踏事件”、“8·12天津滨海新区爆炸事故”等，给人民群众生命财产造成重大损失[5-6]。面对这些突发事件，进行有效疏散对于减轻灾害或事故的损失具有重要意义。

目前，国内外学者在疏散路径优化方面进行了大量的研究。然而，由于针对疏散场景不同，均存在特定的假设和一定程度的局限性。文献[7]基于元胞自动机，将提出的CA-ACO模型在船舶人员疏散方面进行了应用；文献[8]基于Dijkstra算法，提出了求取K则最优路径的双向搜索算法，并结合VB程序设计语言，得出矿井不同灾变地点的具体逃生路径；文献[9]以某氯碱厂液氯泄漏为研究对象，采用计算流体力学Fluent软件模拟计算得出区域疏散路线中各监测点的氯气扩散实时浓度，优选出在所有泄漏场景中人员累计中毒风险较小的最优疏散路线；文献[1]提出基于蚁群算法的行人流量高峰期城市交通应急疏散路径优化方法，在疏散路径效率与通道利用率上有明显提高；文献[10]结合地图基础路网数据信息，进行了建模仿真测试，得到了较好的仿真结果；文献[5]以疏散路径所需的总疏散时间最短作为优化目标，设计了求解这一时变最短路问题的改进 Dijkstra 算法，并给出了算法的正确性证明。

综合以上成果，虽然相关文献研究了基于实时灾害影响的转移避灾路径，引入了灾变模型及算法，但大多未考虑未来灾害的演变趋势，无法达到避灾的效果[11-14]。因此，本文基于改进Dijkstra算法，采用仿真模拟手段，预测未来一段时间内的灾害变化情况，提前规划出避开灾害且疏散时间较短的路径，为制定科学、合理的疏散路径提供参考和依据。

1 基于灾害预测的疏散路径优化

1.1 变量定义

1)设疏散网络G(V,A)，其中，V={v1,v2,…,vn}为有限节点集合；A为有限弧集合，A⊆V×V；v1,v2,…,vn表示网络中的各个节点，v1为源节点，代表被疏散者的初始位置，vn为目的节点，代表被疏散者需要到达的安全地带[5，15-16]。

2)lij为节点vi,vj之间的弧的长度，(vi,vj)∈A。

3)tij表示被疏散者通过弧(vi,vj)所用的时间；ti表示被疏散者到达节点vi的时刻，tj表示被疏散者沿着弧(vi,vj)到达节点vj的时刻，显然tij=tj-ti。

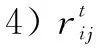
5)决策变量xij等于0或1，其中，xij=1表示弧(vi,vj) 在选定的疏散路径上；xij=0表示弧(vi,vj)不在选定的疏散路径上。

6)疏散路径P定义为从疏散源节点到疏散目的节点的1条有效路径，P为网络中节点的有序序列，设pk为路径P中包含的各节点在疏散网络中的编号，则路径P可用(vp1,vp2,…,vpk,…,vpK)表示，其中1≤pk≤n，k是节点vpk在路径P中的经过顺序编号。p1=1，pk=n，即路径P起始于疏散源节点，终止于疏散目的节点。考虑到疏散计划的可行性和应急疏散的时间紧迫性，疏散路径P应可行且不包含回路。

7)沿路径P=(vp1,vp2,…,vpk)， 1≤pk≤n，由节点vp1至节点vpk所用的时间定义为沿路径P疏散至结点vpk的疏散时间，记作ET(P,vpk)，则：

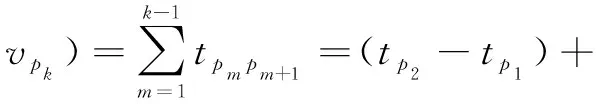
1.2 路段受灾风险与综合阻抗

将地图网格化，统计t时刻每个网格内的毒气浓度，对于第k个网格，t时刻的毒气浓度记为ρ(k,t)；将路段(vi,vj)网格化，路段对应的网格集合设为Gij。那么路段(vi,vj)的受灾风险值rij计算方法如式(1)所示。

(1)

式中：λ是跟毒气种类毒性大小相关的系数，λ>0，毒性越大，λ越大。

基于以上定义，路段(vi,vj)的时变路段阻抗函数如式(2)所示。

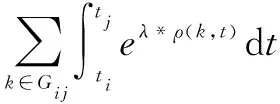
(2)

上文中，式(1)表示人员在通过路段(vi,vj)时的总受灾风险；式(2)表示路段(vi,vj)的总阻抗。

1.3 模型

在以上变量和名词定义的基础上，以通过路径所需的总疏散时间最短和受灾风险水平最低为优化目标，建立考虑灾害扩散实时影响的应急疏散路径选择问题的数学模型。

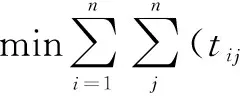
(3)

(4)

(5)

xij=0,1;i=1,2,…,n;j=1,2,…,n

(6)

式中：约束(4)表示xij的取值构成从源节点v1到目的节点vn的1条可行疏散路径；约束(5)表示疏散路径中不含回路；约束(6)为决策变量xij的类型约束。

1.4 算法

在考虑灾害扩散影响的应急疏散路径选择问题中，由于各弧段上的受灾风险值是时变函数，通过弧(vi,vj)所承受的灾害风险值rij不仅与弧长度lij有关，还与到达该弧段起点vi的时刻有关，即与从v1到vj的特定经行路径P有关，故传统的Dijkstra算法不能直接应用于求解建立的模型。为此，本文设计求解时变灾害耦合最短路问题的改进Dijkstra算法，将Dijkstra算法中路径权重的加和求取方法按照上文所述的疏散受灾风险递推求解方法进行修正。

节点vj的P标号记为P(vj)；T标号记为T(vj)；算法的第i次循环后具有P标号的节点集合为Si；以λ(vj)记录从v1到vj的路径P上节点vj的前1个节点；设M为1个很大的正数。

1)步骤1：初始化(算法迭代步数i= 0)，令S0={v1}，P(v1)=0；对于∀vk≠v1，令T(vk)=+，λ(vk)=M；令中间变量m=1。

2)步骤2：如果vn∈Si，则算法终止，此时P(vn)即为从v1至vn所需的最短时间，Un表示从v1至vn的最小综合阻抗值，对应的路径即为最佳疏散路径；否则，转入步骤3。

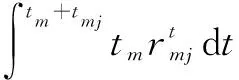
2 算例分析

2.1 算例背景

本算例以某市南站油库为背景，假定场景为某市南站附近油库爆炸导致有害气体泄漏，如图1所示。其中，有1个集合点，标为红色，在南站油库的南侧路口，记为A；有1个安置点，位于沈家屯小学附近，记为C。

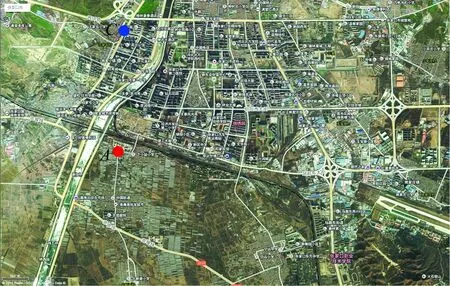
图1 某市南站油库周边路况Fig.1 The surrounding road of the oil depot of South Railway Station in one city

为了便于测试路径优化模型算法，本文利用自主研发的系统软件(基于以上模型及算法，利用C#程序设计语言和Visual Studio 2013平台，开发的模型算法实现原型系统)构建某市的疏散交通网络，该网络共包含160个路段，双向约320个有向弧，各路段编号及长度信息如表1～2所示。

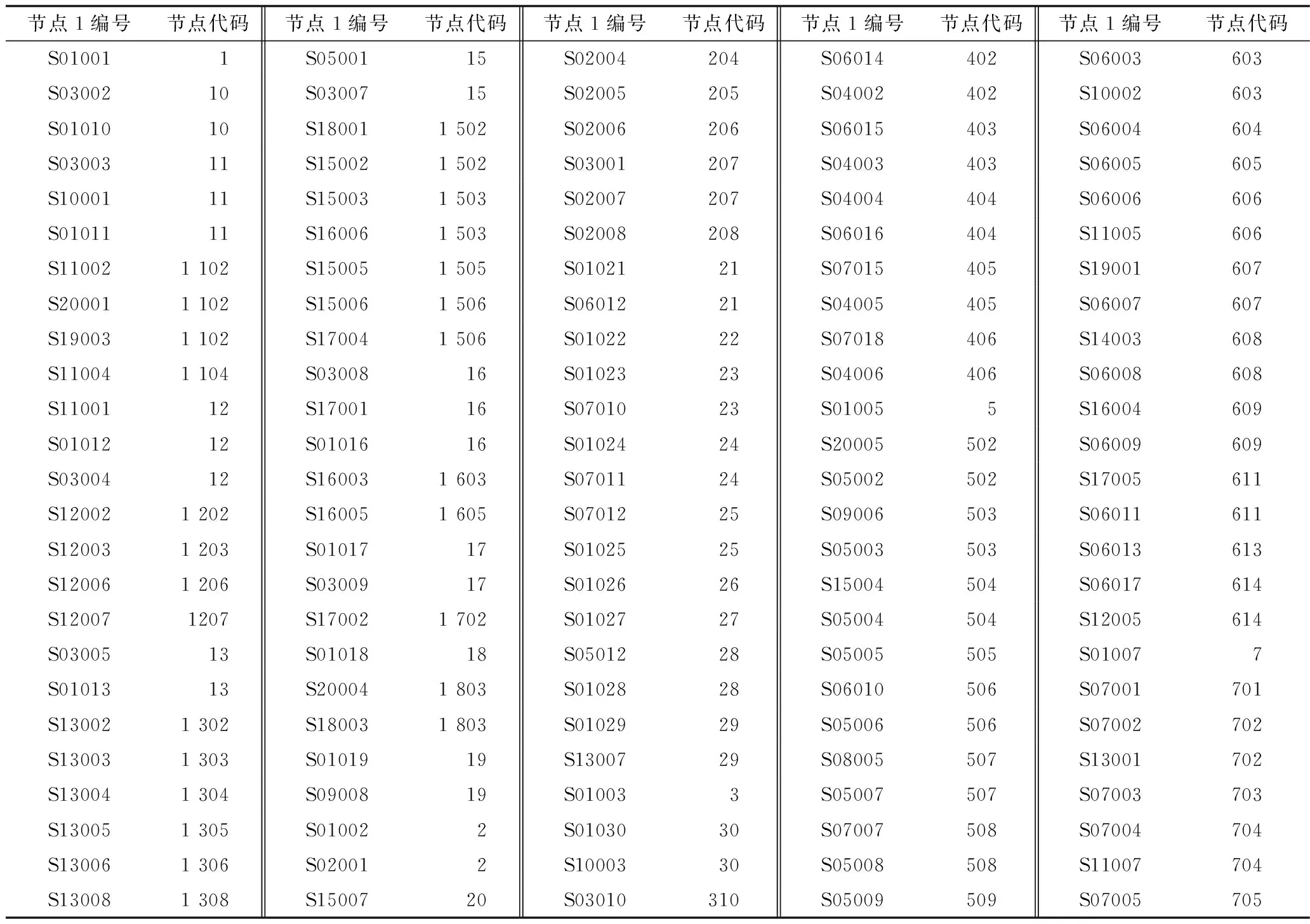
表1 路段节点编号与代码对应关系Table 1 The correspondence between the number of link nodes and codes

表1(续)

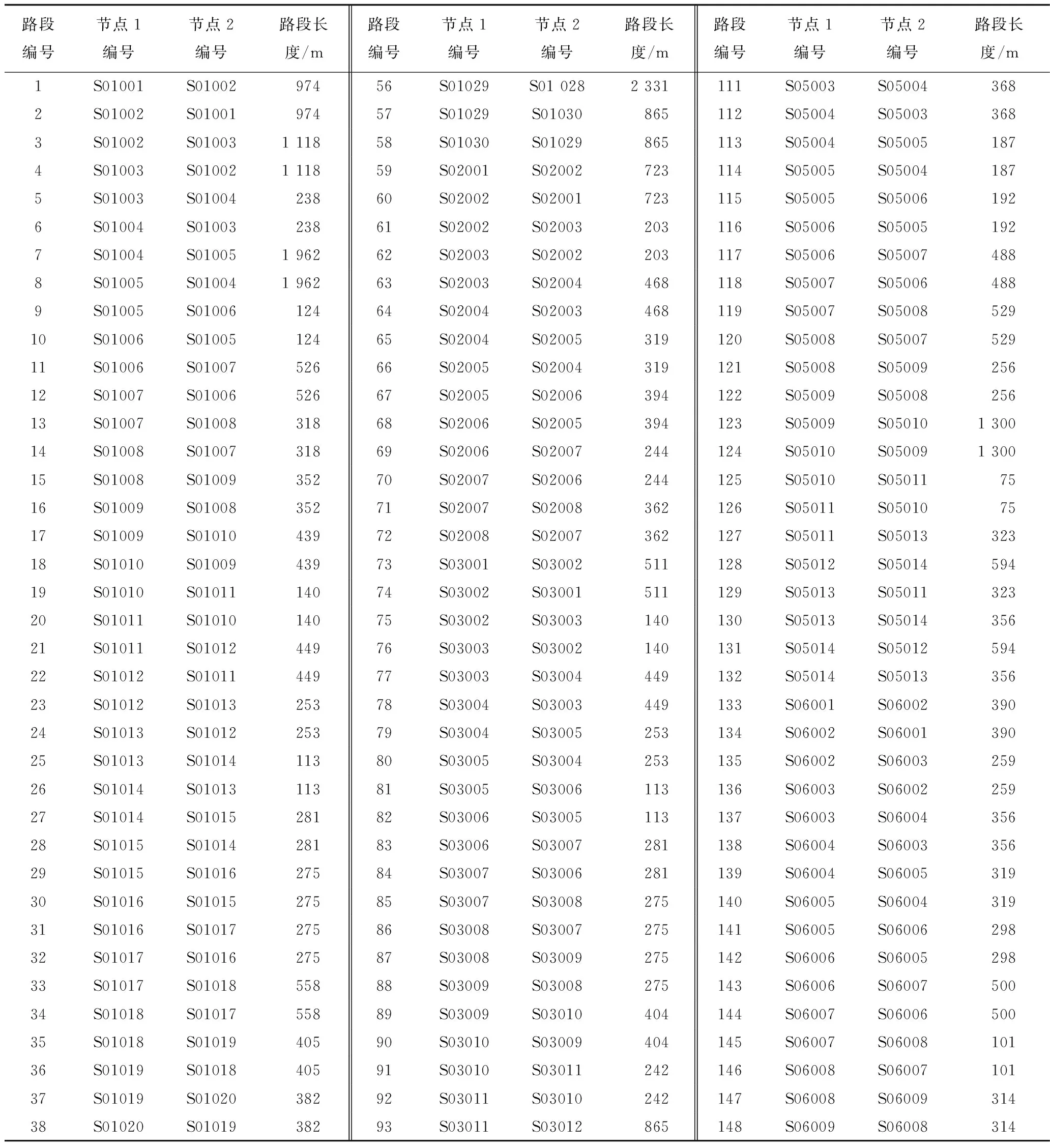
表2 路段长度信息Table 2 The length of road section information

表2(续)

2.2 有毒气体扩散及路段受灾风险评估

可以用不同的颜色表示不同受灾程度，颜色区分以某重气为例可以表示为如表3所示。

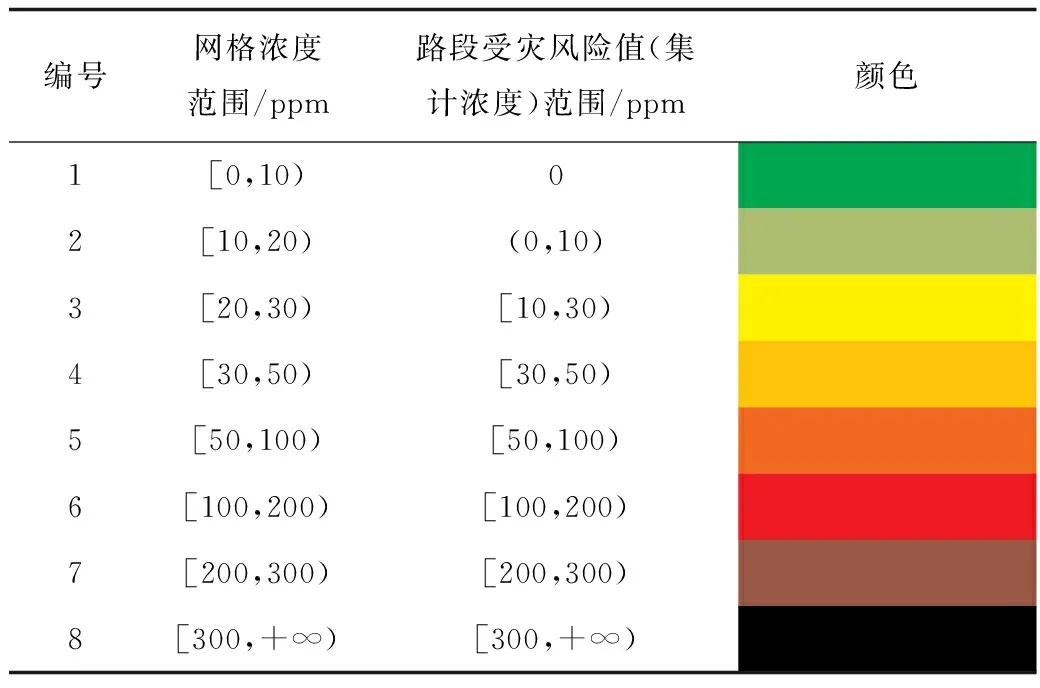
表3 网格浓度及路段受灾风险Table 3 Grid concentration and road risk of disaster

有毒气体扩散及路段受灾风险分析如下。

1)有毒气体模拟扩散结果。有风条件(风向为西北风、风速为6 m/s)与无风条件下的毒气扩散模拟结束时的结果如图2所示。颜色从绿到黑变化，参照表3，自上而下，越接近黑色，表示毒气浓度越高。

2)路段受灾风险评估结果。图3为有风与无风条件下各路段受灾风险的评估结果，颜色从绿到黑变化，参照表3，自上而下，越接近黑色，表示该路段的受灾风险越高。

选取某一受灾路段3003→3002为例，其受灾风险随时间的变化情况如图4所示。

如图4所示，在该风速、风向与泄漏源条件下，毒气扩散的方向是向东南方向，且由于初始毒气泄漏源浓度极高，并且路段临近毒气泄漏源下风向位置，因此该路段受灾风险值先增加后下降；而在无风条件下，毒气以泄漏源位置为中心向四周逐渐扩散，因此受灾风险值持续缓慢增加。

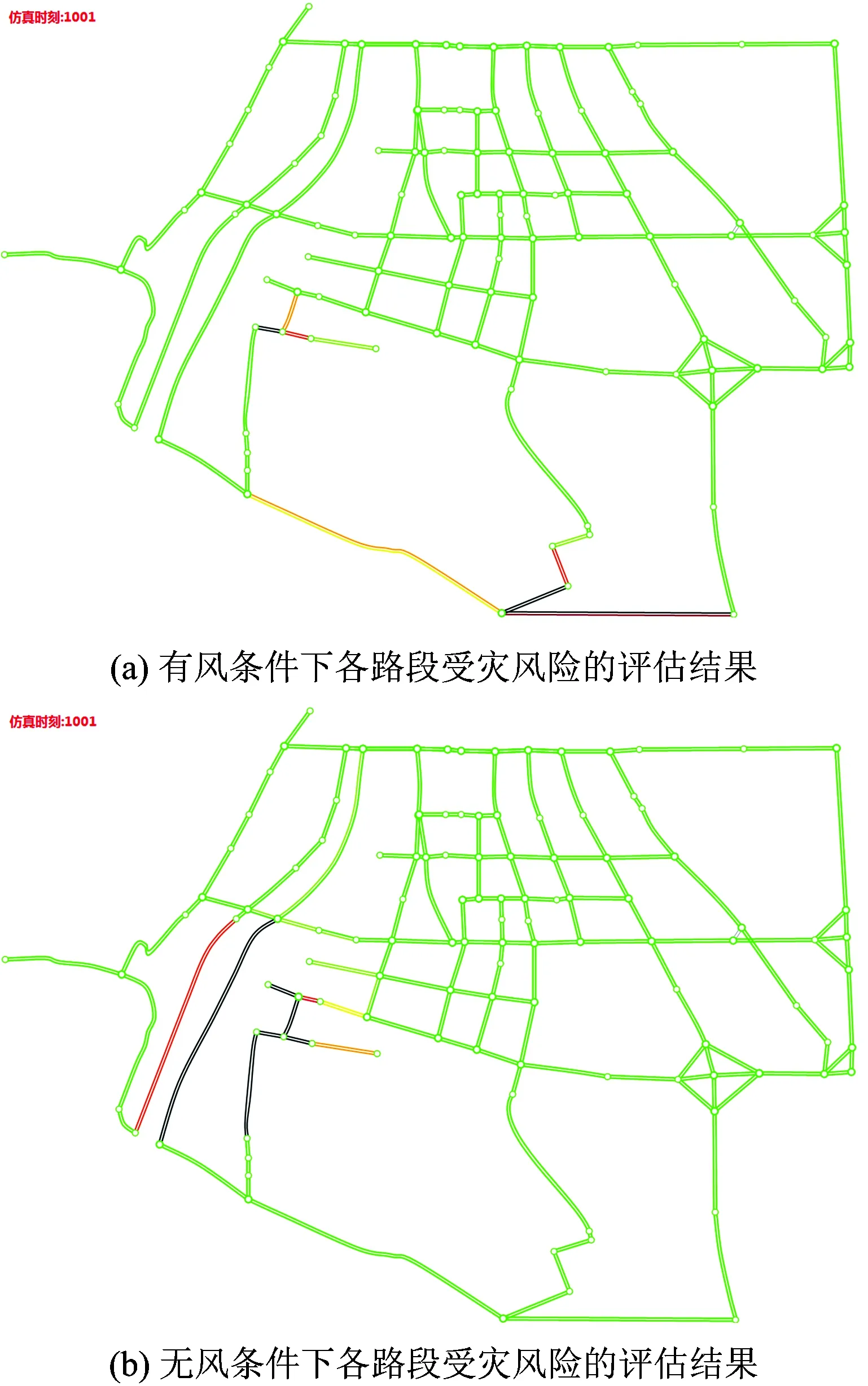
图3 路段受灾风险评估结果Fig.3 The risk assessment results of road section disaster

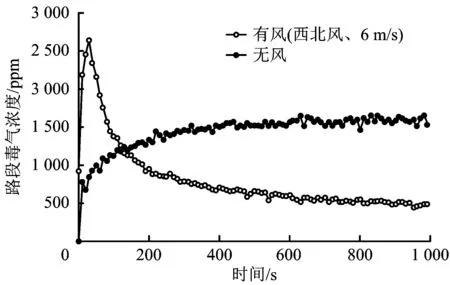
图4 路段3003→3002毒气浓度随时间的变化情况Fig.4 The change of gas concentration with time in the road section 3003→3002

2.3 人群转移避灾路径优化分析

基于该场景，测试本文提出的快速转移避灾路径优化模型与算法，并将有风和无风条件下考虑未来灾害演变、不考虑灾害影响4种情形的路径优化结果进行对比分析，如表4所示。

对于考虑未来灾害演变的路径优化模型来说，其相对其他模型更贴近实际情况，解算出来的路径应该优先考虑的，例如：场景②和场景④。

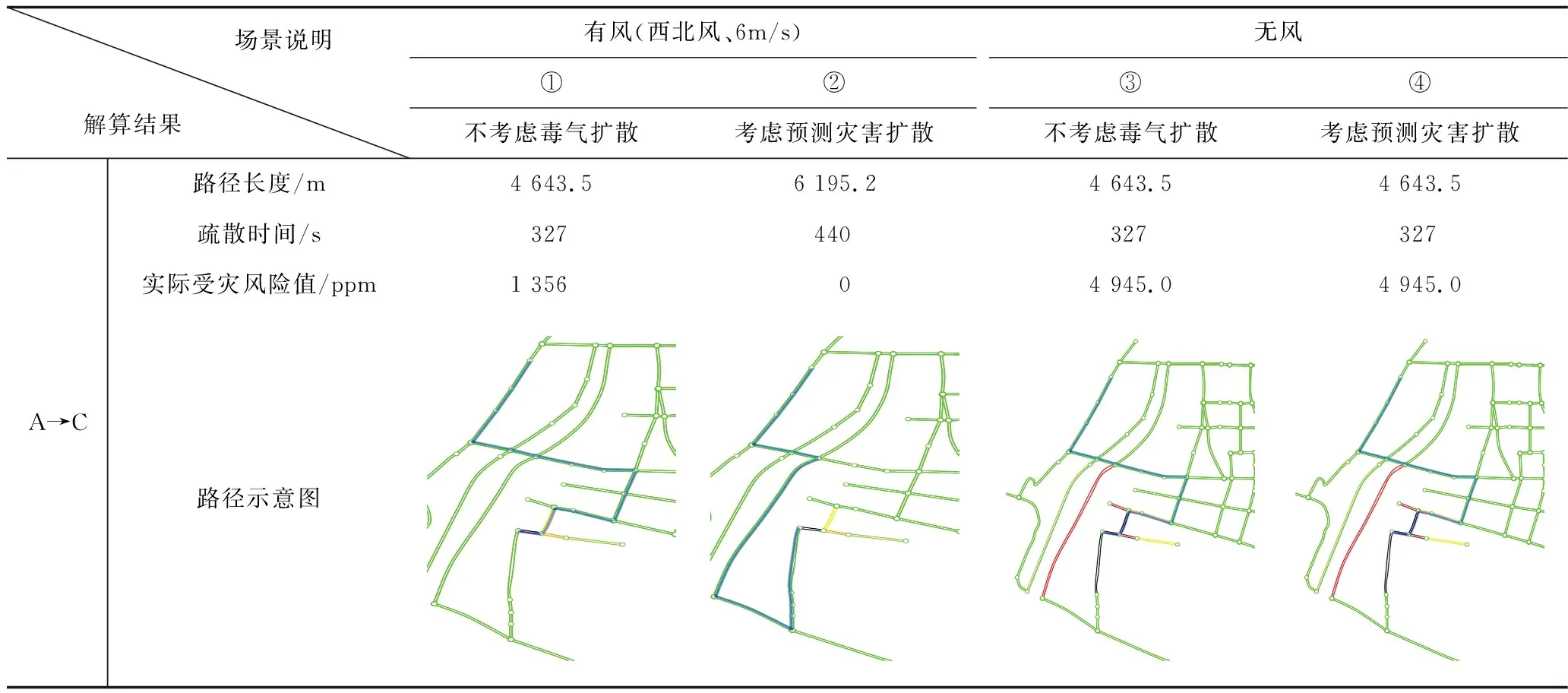
表4 不同场景下最优快速人群转移避灾路径解算结果Table 4 The calculation results of optimal fast crowd evacuation route in different scenarios

3 结论

1)针对目前大多疏散路径解算在未来可能灾害演化趋势方面考虑不足的问题，提出基于未来灾害演变特征仿真预测的转移避灾路径优化算法，通过仿真预知可能受灾情景，提前预测避开灾害且疏散时间较短的路径。

2)以某市南站油库为算例，对快速转移避灾路径优化模型与算法进行说明，并将有风和无风条件下考虑预测灾害扩散、不考虑灾害影响等4种情形的路径优化结果进行对比分析。