基于熵权TOPSIS模型的机床结构件优选设计

2018-11-01朱金波王秋林殷国富

组合机床与自动化加工技术 2018年10期

朱金波,顾菘 ,王秋林,王玲,殷国富

(1.成都航空职业技术学院工程实训中心，成都 610100; 2.四川大学制造科学与工程学院，成都 610065)

0 引言

机床重要结构件综合性能的优劣直接影响机床整体性能，设计时需要综合考虑多项性能评价指标和多个设计方案的取舍[1]，然而设计师在面对一系列指标和方案时往往很难做出选择。TOPSIS法是一种多属性决策方法，被广泛应用到很多领域的研究中，目前在机械领域也有学者使用TOPSIS法解决工程问题。许亚钢[2]采用TOPSIS法计算分析优选出球形蜗杆砂轮磨齿机床身最优结构，提高了球形蜗杆砂轮磨齿机床身的静动态特性。陈永亮等[3]提出了采用相对距离尺度的改进TOPSIS评价方法优选立式磨床横梁结构，优选结果与实际生产所选择方案相符合。李宇鹏等[4]提出了基于TOPSIS法的大型机床床身优选设计，建立了评价床身的TOPSIS优选模型，选出了最佳方案。上述三位学者采用的TOPSIS法能够较好的解决机床结构件优选设计中的多项性能评价指标和多个设计方案的取舍难题，但缺点是在确定机床结构件性能评价指标的权重时设计人员的主观性较强。本文提出的熵权TOPSIS法不仅能够解决多个方案和多项性能评价指标之间难以取舍这一问题，而且引入了熵权法，可以客观的确定机床结构部件评价指标权重。

1 机床结构件优选设计思路

机床结构件优选设计整体思路如图1所示。首先依据机床功能改进或创新设计要求，结合经验进行机床结构件分解，提出每一个结构件初始整体设计方案；然后在此基础上对机床初始结构件整体设计方案进行静动态特性分析，如利用有限元软件进行静力学分析、模态分析、拓扑优化和热分析等；结合静动态分析结果对机床结构件初始整体设计方案提出多个结构改进方案；利用灵敏度分析、多目标优化功能依次对提出的改进方案进行优化设计，并将优化后的改进方案组成备选方案集；通过基于熵权TOPSIS法对备选方案集进行优选设计，确定最终设计方案。

引入熵权TOPSIS法对机床结构件进行多方案取舍和多指标综合评价[4]。机床结构件的常用评价指标有质量、固有频率、应力、静刚度和热特性等多项[3]，为了综合量化评价机床结构件不同备选设计方案的优劣，提出了基于熵权TOPSIS法对备选方进行优选。

图1 机床结构件整体优选设计思路

2 熵权TOPSIS法

2.1 熵权TOPSIS法原理

熵权TOPSIS法实质上是在确定评价指标权重时引入熵权法，是一种改进的TOPSIS法。TOPSIS法是通过测算评价备选方案和理想方案的接近程度来衡量评价对象的相对优劣，是一种常用的有限方案多目标决策分析方法[5]。熵权法是依据评价对象各评价指标提供的信息客观确定其权重，消除人为主观因素的影响，在决策时能够客观评价指标体系中每项的重要程度[6]。

2.2 熵权TOPSIS法优选步骤

(1)构建决策矩阵。假设被评价对象有m种方案依次为a1,a2,…,ai，其中(i=1，2，…m)；每一种方案有n个评价指标依次为ai1,ai2,…,aij，其中(j=1，2，…n)；则构建的判断矩阵A为：

(1)

(2)规范化决策矩阵。为避免因评价指标单位及量级不同而产生的误差或者结果失真[4]，此处对决策矩阵A中的所有元素aij按式(2)进行范化计算，得到规范化决策矩阵的元素bij，从而构建规范化后的决策矩阵B。

(2)

(3)熵权法计算评价指标权重。熵被用来度量系统的无序程度。指标的熵值越小，表明该指标提供的信息量越大，在系统中越重要，理应权重越大[7]。指标的熵值可以根据式(3)计算。

(3)

(4)

其中，ωj[0，1]，且

(4)构建加权规范化决策矩阵。结合规范化决策矩阵和计算出的评价指标权重，可根据式(5)求出评价指标加权规范化决策矩阵H为：

(5)

其中，hij=ωj·bij(i=1，2，…m；j=1，2，…n)。

(5)确定理想解。评价指标最满意的值被称作正理想解[8]，评价指标最不满意的值被称为负理想解。用D+和D-依次表示正理想解和负理想解，可按式(6)计算。部分评价指标数值越大越好，称为效益型指标；部分评价指标数值越小越好，称为成本型指标。效益型指标和成本型指标依次用wt和wc表示。

(6)

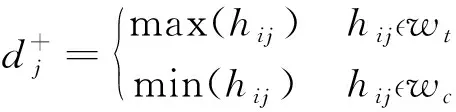
(6)计算欧氏距离。按式(7)计算各方案的评价指标和正负理想解间的欧氏距离。

(7)

(7) 计算贴近度。某方案相对理想解的贴近度计算公式为：

(8)

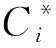
3 龙门机床定横梁备选方案设计

3.1 龙门机床整体结构

图2所示为课题组研究的大型双龙门机床，该机床由动龙门、定龙门、床身、平台和转台等部件组成。动龙门和定龙门整体可以沿着床身导轨方向移动，动横梁可以沿着动龙门立柱上下移动，定横梁则固定于定龙门顶部，不能移动。

图2 龙门机床的结构

定横梁是定龙门主要部件之一，其动静态性能直接影响定龙门加工精度。本文以该双龙门机床的定横梁优选设计为例，阐述熵权TOPSIS法在机床结构优选设计中的应用，图3所示为机床的定横梁部件。

图3 定横梁部件

3.2 定横梁备选方案设计

机床零部件内部筋板元结构对机床的性能有重要影响[9]。为了不重新设计机床定龙门中的定横梁、滑枕、导轨等部件之间的配合结构，在进行定横梁备选方案的设计时，主要对定横梁内部筋板结构的筋板排列方式、厚度尺寸、位置尺寸和拓扑结构进行设计，而不改变定横梁的外部配合结构。图4所示为定横梁部件初始方案的内部筋板结构。

图4 定横梁部件初始方案

定横梁备选方案设计思路为：①利用拓扑结构分析找出定横梁最佳拓扑结构，剔除冗余质量，达到定横梁轻量化设计和提升静刚度设计的目的；②利用模态分析找出定横梁低阶振型图中变形最大区域，分析原因，提出改进方案，从而提高定横梁动刚度；③结合热特性分析减小定横梁热变形。本文利用ANSYS Workbench软件建立定横梁部件初始设计方案的有限元模型，进行静力学分析、模态分析、拓扑优化分析和热分析[10-11]，依据分析结果提出如表1所示的10个改进方案。

表1 定横梁改进方案

3.3 备选方案的优化设计

定横梁备选方案的优化设计思路为：①利用灵敏度分析找出筋板厚度、位置和拓扑结构中对定横梁质量、固有频率、最大变形量等性能参数影响较为敏感的尺寸；②以灵敏度分析中找出的性能敏感尺寸为设计变量，以定横梁的质量、静刚度、固有频率和热变形为目标函数，建立多目标优化模型。其中设定质量目标、静刚度目标和热变形目标为越小越好，而固有频率目标越大越好。利用ANSYS Workbench软件依次建立10种定横梁部件改进方案的有限元模型，对定横梁部件改进方案进行灵敏度分析和多目标优化设计[12]。最后对优化后的10个定横梁部件备选方案进行静力学分析、模态分析和热特性分析，分析结果如表2所示。

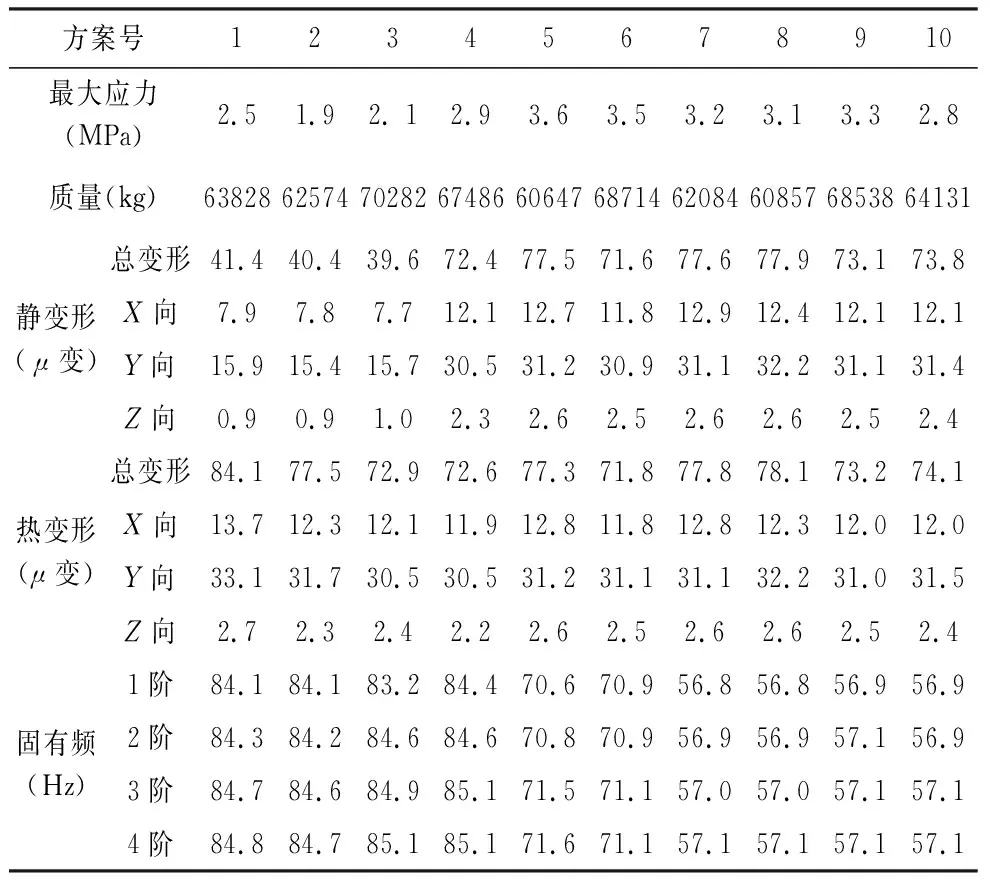
表2 定横梁部件备选方案性能参数分析结果

4 定横梁备选方案优选设计

4.1 构建规范化决策矩阵

对于机床结构件而言，应保证较好的静动态特性的同时质量尽可能的轻。因此，在进行定横梁备选方案优选设计时，选取定横梁的质量、静变形、应力、热变形和固有频率作为重要评价指标。观察表2所示的定横梁备选方案性能参数数据，发现所有备选方案第1阶到第4阶固有频率数值差别较小，因此在构建评价矩阵时仅以所有评价方案的第1阶固有频率为依据。在Matlab中依据2.2节中的公式(1)构件评价矩阵A：

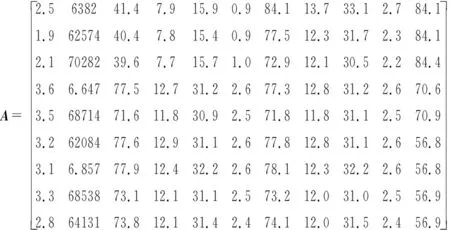
为避免矩阵A中评价指标单位不同及数值量级不同而导致计算误差或者结果失真，依据2.2节中的公式(2)对评价矩阵A进行规范化处理，得到规范化矩阵B(由于矩阵过大，此处省略)。

4.2 确定加权决策矩阵

确定加权决策矩阵实质上是考虑了各个评价指标对机床结构件性能影响权重的决策矩阵。本文为克服在确定评价指标权重时人为主观因素的影响，采用熵权法确定定横梁评价指标权重。依据2.2节中的公式(4)计算定横梁各评价指标的权重。表2中列向为定横梁评价指标，从最大应力到固有频率(1阶)共11个评价指标的权重依次为：ω=(0.0532，0.2096，0.1026，0.0744，0.0888，0.0489，0.1039，0.0755，0.0900，0.0503，0.1029)。然后根据2.2节中的公式(5)确定加权决策矩阵H(由于矩阵过大，此处省略)。