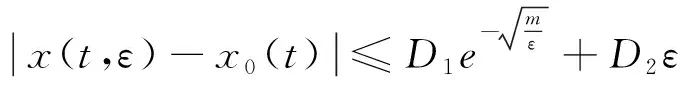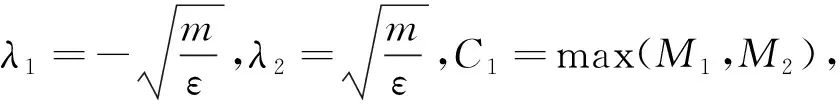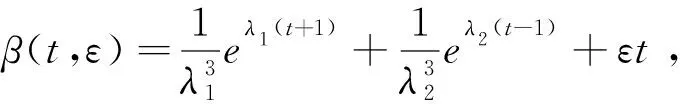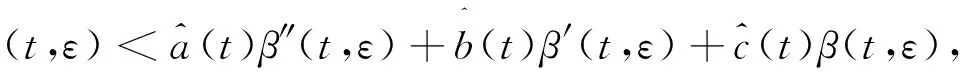某一类非线性三点边值条件的三阶奇摄动边值问题
2018-10-31王国灿
王国灿
(大连交通大学 理学院,辽宁 大连 116028)*
0 引言
三阶非线性微分方程三点边值问题的奇摄动日益被人们所关注[1-6],但由于上下解理论的限制,目前只看到几篇讨论简单的三点边值问题或线性边值问题的文章,有关解的唯一性方面的内容很少涉及.本文讨论以下一般的三阶非线性微分方程的非线性三点边值的奇异摄动问题.
εx‴=f(t,x,x′,x″,ε)
(1)
(2)
将研究方程(1)具有非线性边值条件(2)的解的存在性与唯一性.
1 引理
下面考虑三阶边值问题
x‴=f(t,x,x′,x″)
(3)
(4)
定义如果存在函数β(t)和α(t)∈C3[-1,1],使得当-1≤t≤1时,α′(t)≤β′(t),β″(t)≤f(t,β(t),β′(t),β″(t)),α‴(t)≥f(t,α(t),α′(t),α″(t)),且当-1≤t≤0时,
β(t)≤α(t),当0≤t≤1时,α(t)≤β(t),则称β(t)和α(t)为方程(3)的上下解.
方程(1)满足Nagumo条件,如果函数满足下述两个条件之一者:
(*)对正数N,存在正函数h=h(N),使得当(t,x,x′,x″)∈[0,1]×[-N,N]×R2成立
|f(t,x,x′,x″)|≤hΦr1(|x′|)Φr2(|x″|),其中0≤r1≤1,r2>0,r1+r2≤3,且Φr(l)=max{1,lr},r>0,0≤l≤+∞
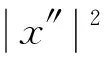
引理1如果方程(3)与边界条件(4)满足
(1)函数f(t,x,x′,x″)∈C([-1,1]×R3),满足Nagumo条件,且当-1≤t≤0时,关于x单调不减;当0≤t≤1时,关于x单调不增.
(2)g(ξ,η),h(ξ,η)∈C(R2),且g(ξ,η),h(ξ,η)对固定的ξ关于η单调不减.
(3)方程(3)存在上下解β(t)和α(t),且β(0)=A=α(0),g(α′(-1),α″(-1))≥0,g(β′(-1),β″(-1))≤0,h(α′(1),α″(1))≤0,g(β′(1),β″(1))≥0,则边值问题(3)、(4)有一解x(t)∈C3[-1,1],使得β(t)≤x(t)≤α(t),-1≤t≤0,α(t)≤x(t)≤β(t),0≤t≤1.
引理2如果满足
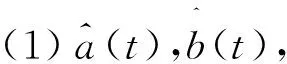


则边值问题

(5)
(6)
只有零解.
引理1与引理2 可以利用文献[9]的处理方法得到.
2 结论
为方便起见,恒假设下列条件成立
(1)函数f(t,x,x′,x″,ε)及其关于x,x′,x″,ε的一阶偏微商在闭区域Ω={(t,x,x′,x″,ε)|-1≤t≤1,-∞ (2)函数f(t,x,x′,x″,ε)满足Nagumo条件. (3)边值问题0=f(t,x,x′,x″,0),x(0)=A有解x0(t)∈C3[0,1]. (4)函数g(ξ,η,ε),h(ξ,η,ε)∈C(R2×[0,ε0]),且均关于η单调不减. (5)当(t,x,x′,x″,ε)∈Ω时,fx′(t,x,x′,x″,ε)≥m>0;fx″(t,x,x′,x″,ε)有界;当-1≤t≤0时,fx(t,x,x′,x″,ε)≥0,当0≤t≤1时,fx(t,x,x′,x″,ε)≤0. (6)(i)对任何的正数L0,存在正数N0,使得g(ξ,-N0,ε)≤0,g(ξ,N0,ε)≥0,|ξ|≤L0,0≤ε≤ε0. (ii)对任何的正数L1,存在正数N1,使得h(ξ,-N1,ε)≤0,h(ξ,N1,ε)≥0,|ξ|≤L1,0≤ε≤ε0. (7)函数g(ξ,η,ε)及h(ξ,η,ε)在[0,ε0]×R2上连续可微,且 gξ(ξ,η,ε)≤0,gη(ξ,η,ε)≥0,gξ2+gη2≠0 证明由假设,当(t,x,x′,ω(ε)x″,ε)∈Ω时,存在正数k,M,N,使得|fx′(t,x,x′,x″,ε)|≤k,|fε(t,x,x′,x″,ε)|≤M,|x‴0(t)|≤N,记 对于任何的ε∈[0,ε0],再令β(t,ε)=x0(t)+γ(t,ε),α(t,ε)=x0(t)-γ(t,ε),于是当ε>0充分小时,α′(t,ε)≤β′(t,ε),β′(t,ε)>0,-1≤t≤1;β(t,ε)≤0,-1≤t≤0,β(t,ε)≥0,0≤t≤1,且β(0,ε)=0,且 其中,K满足 |fx″γ″(t,ε)|≤Kε. 同理f(t,α(t,ε),α′(t,ε),α″(t,ε),ε)-εα‴(t,ε)≤0,由β(t,ε)的构造, β″(1,ε)≥N1,于是 定理2如果满足条件(5)和(7),则当ε>0充分小时,边值问题(1),(2)至多存在一个解. 证明在此,只对足够小的ε>0进行论证,假设边值问题(1)、(2)有两个不同解x1(t,ε),x2(t,ε),令y(t)=x2(t,ε)-x1(t,ε),则y(t)应满足下述边值问题 其中, a1≤0,b1≥0,a2≥0,b2≥0,且a1+b1>