地铁齿轮箱组件的静强度分析与试验研究

杨亮，付博华，李忻，付赟秋,张辙远

(1.大连交通大学 机械工程学院，辽宁 大连 116028; 2.中车北京南口机械有限公司,北京 102200)*

0 引言

随着交通工具的不断升级，速度、舒适和安全成为了人们追求的目标.地铁的出现给人们的出行带来相当大的好处，尤其是在上班高峰期等地面通行较堵的时候，地铁有效缓解了城市的交通拥挤.

地铁因其高速运行，安全性就显得尤为重要.地铁齿轮箱是地铁车辆转向架中的关键部件，其主要作用是将牵引电机输出的扭矩变大，并将电机的高转速转变为车轮的低转速，从而在电机额定转速下驱动地铁车辆的运行.地铁车辆运行中启动和制动较为频繁，线路会有上下起伏，这会产生冲击和振动.吊杆组件除了悬挂固定齿轮箱位置，其球铰副能有效减低车辆运行中轮对对地铁齿轮箱冲击与振动.齿轮箱组件在车辆运行中起着关键作用[1]，因此对其静强度分析及静强度测试十分必要.

由于现实中直接对齿轮箱组件进行静强度测试存在较大难度和未知，因此有必要对其预先进行有限元分析.通过仿真模拟，可以分析出齿轮箱组件的受力分布情况，并能有效地找出组件的应力集中点，对静强度试验测点的选取有重要的指导作用.

1 齿轮箱组件强度分析

1.1 吊杆静强度载荷工况

设计要求给出了±10 000 N·m的计算载荷分类，实际计算时可将这些载荷转化为吊杆上实际承受的作用力.计算如下：

扭矩作用下吊杆的受力按公式计算：

F=M×(i+1)/L

(1)

式中,M为扭矩;i为齿轮传动比,取值5.318;L为支架中心到输出轴距离，取值505 mm，计算得出吊杆在扭矩作用下受力为125 108.9 N.

吊杆分别承受电机正转和反转两种工作情况下对应的作用力，为了保证设计的可靠性，计算时取每个工况下所有载荷叠加起来的最大时作为计算载荷[4].规定：输入轴顺时针转动时，扭矩为正，此时给吊杆的力向上，垂向加速度方向与重力方向相反；输入轴逆时针转动时，扭矩为负，此时给吊杆的力向下，垂向加速度方向与重力方向相同.

吊杆计算总载荷按照以下公式得出：

F总=F扭+F振

(2)

计算得出，输入轴顺时针转动时，吊杆向上的受力为-193 092.21 N；输入轴逆时针转动，向下的受力为194 465.61 N.

1.2 有限元建模及仿真分析

1.2.1 吊杆性能参数

吊杆材料为42CrMo锻钢，其性能属性如下：弹性模量为210 GPa, 泊松比为0.3，密度为7 850 kg/m3，Rm为1 080 MPa，Rp0.2为930 MPa，σ-1为356.4 MPa，δ为12%.

1.2.2 模型建立及单元离散

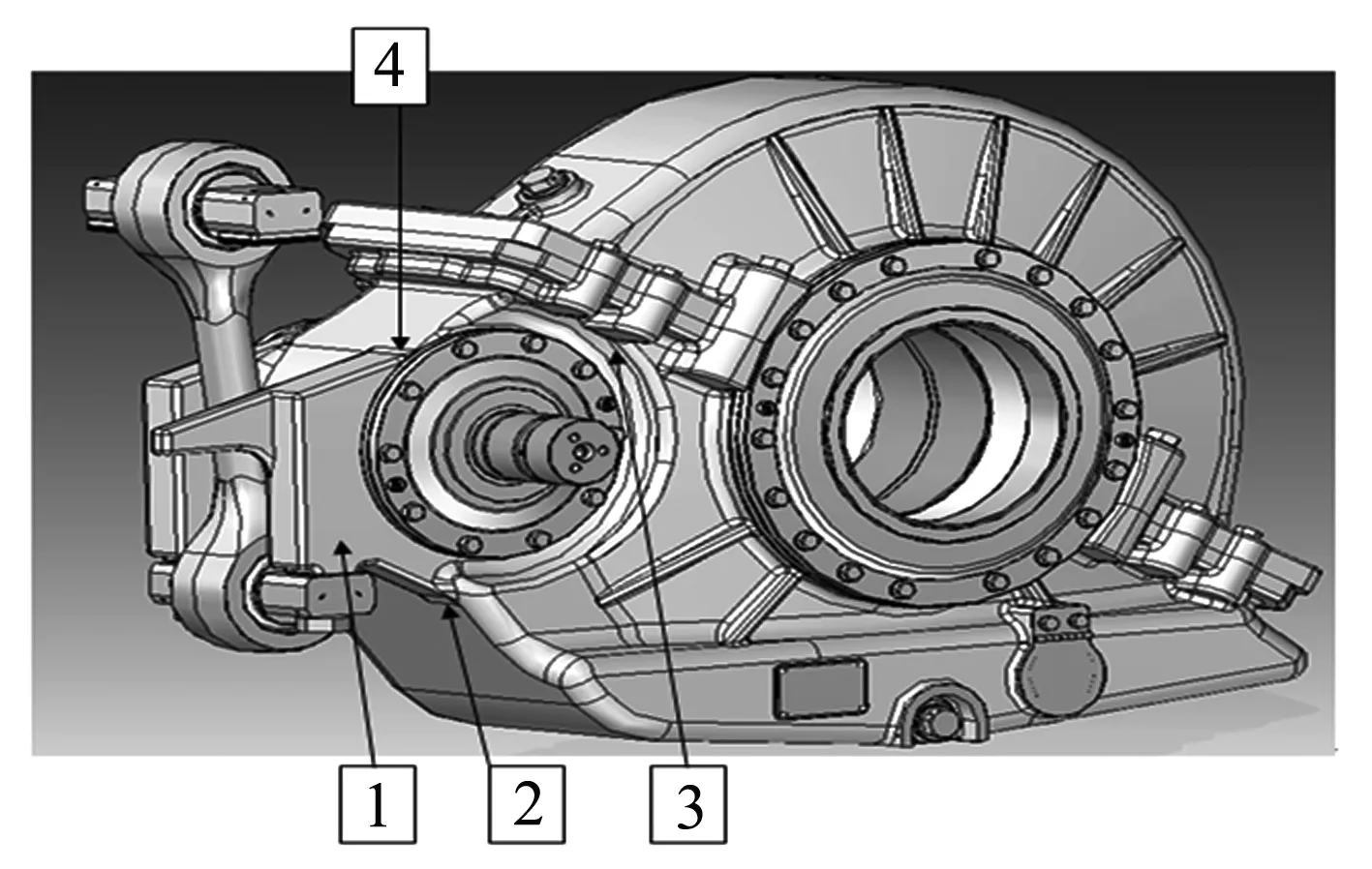
首先建立几何模型，采用的是三维CAD软件Solid Edge.图1为某型地铁齿轮箱的吊杆组件与地铁齿轮箱的三维装配图.

图1 齿轮箱结构

其中吊杆组件是齿轮箱系统关键的承载结构，要求有足够的强度，设计采用的吊杆材料为42CrMo锻钢，箱体材料牌号为QT400- 18L.

以吊杆组件为例，吊杆的计算要全面考虑齿轮传动和箱体因振动所传递给吊杆的作用力，但建立整个系统模型完全没必要，计算时只需将相应的作用力施加在吊杆上即可[2]，因此，建模只考虑吊杆和箱体自身结构即可[3].

计算中各个零件的重量分别为：输入齿轮轴轴系35.9 kg，联轴器总重26.8 kg.

采用的有限元软件：ANSYS 14.0.取吊杆和箱体进行建模和有限元分析，对于应力集中部位，需要进行网格细化，尤其考虑应力集中位置，吊杆和箱体的三维模型在离散后的模型如图2所示.

(a)吊杆 (b)箱体

图2吊杆和箱体的离散模型

1.2.3 边界条件

吊杆的约束条件为：固定吊杆与转向架连接球铰；定义两球铰与吊杆圆柱面接触，接触形式为Rough, 吊杆边界条件如图3所示.

图3 吊杆边界条件

1.2.4 计算结果

有限元模拟结果下(±10 000 N·m)吊杆和箱体最大主应力如表1所示.

表1 有限元模拟结果下吊杆和箱体最大主应力

吊杆在要求工况下正反转最大Von Mises应力有限元分析结果如图4所示. 由应力有限元分析可知，输入轴正转时，吊杆直杆处所受应力较大，是测点分布的主要区域.输入轴反转时，吊杆整体受力较为均匀,相比正转时受力较小，内孔处应力值虽然较大，但由于实际测量时，内孔处无法贴应变计测量，所以可以忽略其影响.

(a)正转 (b)反转

图4输入轴最大VonMises应力云图

图5为箱体正、反转最大Von Mises应力云图，从图中可知，箱体正转时应力较大，且应力较大处集中在输入轴孔的四周，尤以轴孔的上孔壁应力集中，反转时应力集中处也存在于轴孔周围，尤以上孔壁和下孔壁应力集中.因此，在进行静强度试验时需要对这些应力集中处多加试验研究.

(a)正转

(b)反转

2 齿轮箱吊杆应力试验研究

在完成了齿轮箱箱体及吊杆关键部位静应力测点应变片布置后，在齿轮箱箱体由试验台加载正转(从车轴端看顺时针)及反转(从车轴端看逆时针)输入扭矩分别对应变和应力各进行了三组实验，分别测试了箱体和吊杆关键部位测点的应变和应力.

齿轮箱由中车南口公司车间内的加载测试台加载，测试吊杆在给定载荷工况下的应力[5].测试要求如表2所示.

表2 齿轮箱工况

本次测试采用试验与有限元分析相结合的方法，具体的试验测试流程如图6所示.

图6 静态应力测试流程图

2.1 试验设备与试验台的搭建

本次设备采用的是JM3812静态测试仪，该系统为多功能静态电阻应变测试分析系统.设备采样频率为1/2 Hz(静态测试)，可保证采样数据的真实性并排除电源影响.本次测试用应变计分别为应用于箱体的45°三向应变片(120 Ω)及和吊杆的单向应变片(120 Ω).

2.2 试验原理与测点选择

试验精确性受到测试信号的零点漂移现象影响，需要对采集的数据消除零点漂移误差的影响.并且个别的异常数据对试验结果的精确性有很大的影响.可以通过数据幅值正常范围来甄别出异常数据，数据的波形应该是有规律的曲线.

主要考虑到箱体组件的受力，根据有限元分析得出的应力分布，将本次应力测点位置布置在齿轮箱组件应力集中部位.以测点11和测点12与应变仪通道对应说明为例，测点11对应采集通道为1和10，测点12对应采集通道3和9.齿轮箱组件测点具体位置如图7所示.其中箱体上1-10测点每向分别定义为a、b、c，吊杆11、12测点为单向应变片.以现场测点2和11应变片布置照片为例，见图8.

(a)右侧测点分布

(b)左侧测点分布

(a)2号测点 (b)11号测点

图8现场测点应变片布置照片

2.3 数据处理

测试工作结束后，采用数据采集系统自带的数据处理软件进行数据处理，处理流程图见图9.

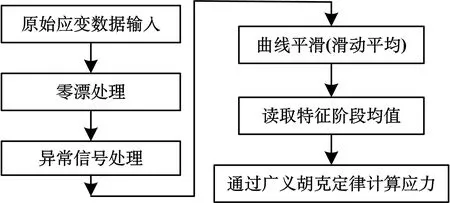
图9 测试数据处理流程

2.4 试验数据处理与分析

测试中对各种不同加载情况进行3次测量，取3次的平均值作为各测点的应力值.表3为测试要求工况下(±10 000 N·m)吊杆正反转最大主应力，其中正负仅代表正反转.

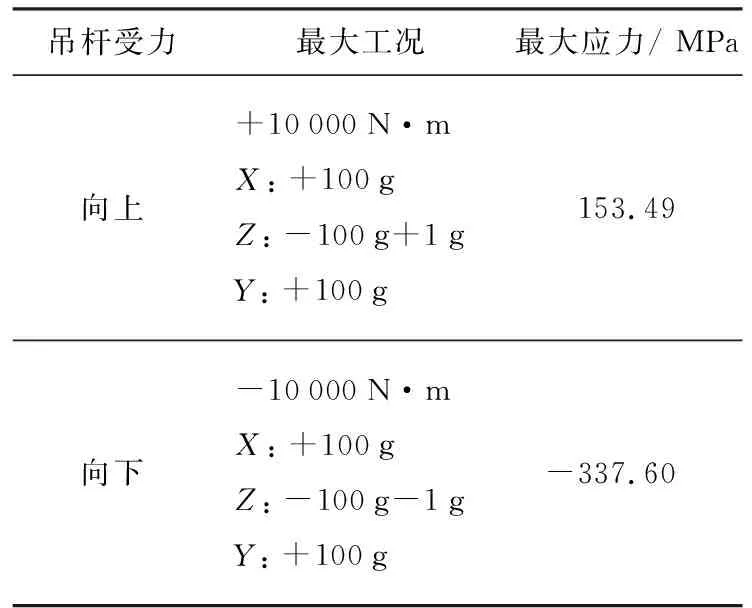
表3 测试要求工况下吊杆最大主应力

箱体2号和吊杆11号测点的应力较大，具有代表性，将2号及11号测点在工况1时最大主应力值列于表4.

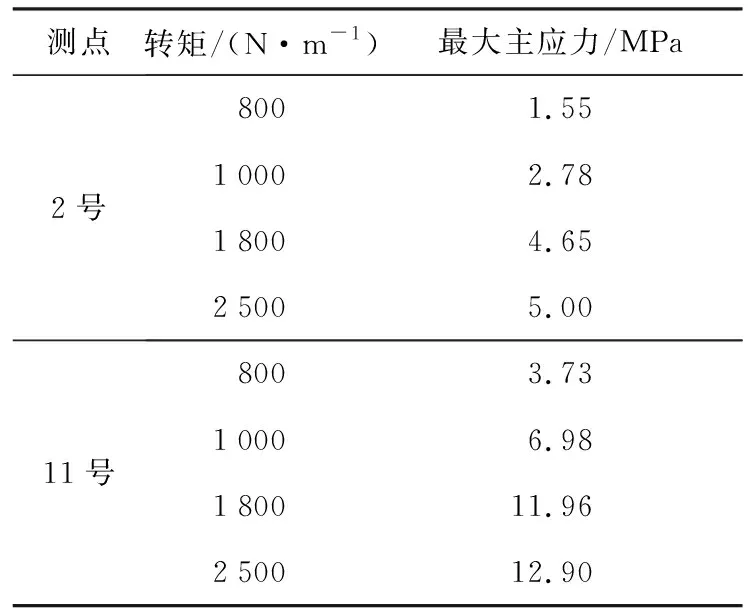
表4 测点在不同转矩时的最大主应力值

测点2的应力随时间变化曲线如图10所示，从图中可看出相关数据波动趋势.试验测试的应力结果明显小于有限元模拟结果，这是因为有限元模拟考虑的是有振动加速度的极端恶劣工况，而台架试验没有考虑振动加速度和线路加速度.并且随着载荷增大，各测点应力均相应变大，基本呈线性关系.测点应力值均呈现正弦的规律波动，并且吊杆的应力值比箱体大，与有限元结果相符.

图10 测点2的应力随时间变化曲线

3 结论

本试验组参照中车北京南口机械有限公司给出的实验要求，在齿轮箱箱体由试验台加载至规定扭矩的情况下分别测试了吊杆关键部位测点的应力，计算了各测点应力值.依据静态评估方法，对比有限元分析及试验结果，得出如下结论：

(1)在正转加载时，应力最大的点为11、12号测点，其次是2、8、7号测点；在反转加载时，应力最大的点为11、12号测点，其次是5，9号测点.吊杆在测试工况要求下反转时最大应力337.60 MPa明显低于吊杆材料屈服极限930 MPa；箱体正转时所受最大应力156.58也低于箱体材料屈服极限250 MPa；

(2)实际应力值均接近或小于有限元分析结果，但误差较小，最大误差不超过8%，误差原因可能是测试现场存在干扰，人为贴片存在误差，扭矩在施加时存在延迟等因素.实际测试箱体为台架测试，可为后续装车运用考核提供参考.考虑到相关的材料参数均按常规设计方法计算或查阅有关手册取值，强度测试结果存在一定的误差，均为实验正常现象，该齿轮箱组件满足大连金普线地铁齿轮箱箱体设计要求.