关于图像分割中的适应度函数修正和遗传算法实现

刘 玲，梁广源

（韶关学院 数学与统计学院，广东 韶关512005）

图像分割是图像处理［1］与机器视觉［2］的基本问题之一，其任务是把图像分解成若干具有特殊性质、互不重叠、具有强相关性集合的过程.分割图像的基本依据和条件之一是考虑分割的图像区域具有灰度级别的相近，其中最大类间方差法［3-4］是有代表性的方法，该方法的思想是通过寻找灰度图像的合适阈值，从而使得图像分割后各类之间的灰度平均值方差达到最大.

为了求解最大类间方差法中的最优化问题，遗传算法［5］是处理该类数学问题的有效方法.遗传算法由Holland提出，模拟自然界生物进化机制，即遵循适者生存、优胜劣汰法则，在优化问题求解中能克服常见数值优化算法局部收敛的困难［6-7］，保证较为稳定的迭代寻优过程.笔者利用遗传算法在最优化问题求解中的优势，通过运用最优化理论修正遗传算法中的适应度函数，进而在最大类间方差法的算法实现中达到加速效果.

1 适应度函数修正

基于最大类间方差利用遗传算法实现图像分割的基本步骤如下：

（1）初始化：根据图像特征进行染色体编码以及产生初始群体；

（2）定义：建立描述类间方差的适应度函数；

（3）迭代：进行选择、交叉和变异等遗传操作；

（4）输出：解码得到最佳的分割阈值.

以上步骤中，第（2）步的适应度函数需要结合图像的灰度特征给出，适应度函数的形式不同，会影响遗传算法的计算效率.

设图像像素按灰度阈值划分为两类，这两类的像素点个数分别为n1,n2，第i类中第k个像素点的灰度值记为目前常用的描述类间方差的适应度函数［8］为：

并且α越接近0，上式的左端越小.另一方面，结合两类间的方差最终达到最大，只需求解：

这里δ表示对图像灰度值的分割阈值.此时，可将式(1)对应的适应度函数定义修改如下：

其中α由求解最优化问题的式(3)确定.

2 MATLAB数值试验

考虑一副323×263的道路图像分割问题，如图1.根据此图像的灰度特征以及道路分割的应用需求，设置类数为2.对于遗传算法的初始参数，设置染色体长度为8，种群大小为8，交叉概率为0.8，变异概率为0.5，适应度函数由式(4)给出.通过MATLAB数值试验展示式(4)给出的适应度函数的数值计算结果.

分别取α=0.25,0.5,1,2，图像分割效果见图2和图3，遗传算法的结果如表1所示.

图1 初始图像及其灰度图

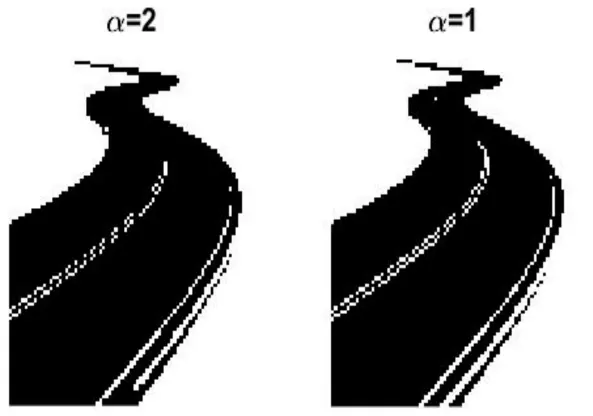
图2 分割效果图(α=1，2)

图3 分割效果图(α=0.5，2.5)

表1 不同参数下遗传算法的计算结果

比对图1的原始数据，随着参数α变小，遗传算法的分割效果越来越好.当α=2和α=1时，如图2所示，图像上方远处的道路中线未能得到识别.当α=0.5时可以初步识别出图像上方远处的中线；当α=0.25时达到最好的中线识别效果，如图3所示.此时对应的灰度阈值为125，一共进行了12代的遗传操作,整体的分割效果跟图1所示的原始灰度图基本吻合.

从遗传算法的迭代效率上看，表1展示了不同参数下的迭代步数对比和对应的灰度阈值，可见当α=0.25时所用的遗传代数最少.因此，本文给出的适应度函数修正是有效的.

3 结语

针对遗传算法求解图像阈值分割的应用问题，本文结合最优化理论修正了描述类间方差的适应度函数，从而改进了应用遗传算法求解最大类间方差方法的计算效率，同时也得到了较好的图像灰度阈值分割效果.本文对适应度函数的改进思想，也可以应用到其他智能算法的实现上.