Canny算子检测焊缝的GPU并行加速研究

白东阳，刘健，王晓曼，景文博

（1.长春理工大学 电子信息工程学院，长春 130022；2.长春理工大学 光电工程学院，长春 130022）

随着科技的发展，焊接技术已在我国国民经济中占据着越来越重要的地位[1]。如今计算机机器视觉的飞速发展，使得该技术越来越多的应用到焊缝检测领域，通过图像处理对工业中的焊缝实体进行数字化的分析计算，利用视觉传感器获取图像数据，运用图像处理算法快速准确的提取焊缝的特征，得到焊缝的间距等信息。

在工业焊接中，获取焊缝间距是进行后续焊接操作的重要参考，而准确快速地检测出焊缝边缘又对计算焊缝间距至关重要，所以如何检测出焊缝的边缘信息显得尤为重要[2]。而焊缝图像往往存在大量的噪声信号，并且焊件的表面材质复杂、光照不均匀等因素都会对图像处理结果造成较大的影响，经过大量的图像处理工程经验的Canny算子可以有效的应用于焊缝的边缘检测中，其精度高、灵活性大的优点作为本算法的首选[3]。但是Canny算子也具有明显的缺点，由于采用高斯滤波、非极大值抑制、边缘连接的计算流程，存在算法复杂度高、运算速度缓慢，与实际工程中快速准确的应用原则相悖，极大的制约了算法的工程实用性。同时，单一的CPU处理和OpenCV处理执行效率也不高，不能用于快速场景检测以及工程项目开发中。

为了提高Canny算子的计算速度，利用GPU并行化处理是一种很好的选择[4]。GPU拥有多个线程，可以对低耦合、高并行的大型数据进行快速计算；同时，近年来GPU的并行计算日臻成熟，其友好的编程操作、亲民的价格也为使用GPU并行处理Canny算子检测焊缝提供了可能。要想使用GPU并行处理Canny算子检测焊缝必须对Canny算子的处理过程优化和并行化改造，以此契合GPU的并行化处理要求。通过对Canny算子的优化改造，运行GPU+CPU的处理模式使得一幅1280×960的图像边缘检测时间缩短到10ms以内，大大提高了算法执行效率，为实际工业使用奠定了基础。

1 Canny算子流程和耗时分析

1.1 高斯滤波

在对焊缝的采像过程中，由电子器件产生的高斯噪声是主要的噪声因素，在对焊缝图像的处理中，经常采用3×3或5×5的卷积模板进行高斯滤波，以便消除高斯噪声。滤除高斯噪声是准确获得焊缝边缘检测结果的基础。

通过公式（1）对焊缝图像每个像素进行卷积运算。经过高斯滤波处理，焊缝图像较之原图像会显得模糊，但是焊缝图像中的高斯噪声得到了有效抑制。

公式（2）为Canny算子x方向和y方向所采用的卷积算子：

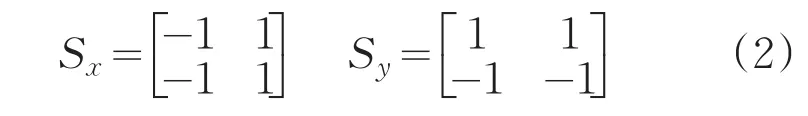
Canny算子的梯度幅值和梯度方向的计算为：

1.2 非极大值抑制

非极大值抑制（NMS）主要是为了更精确的定位焊缝边缘特征，用梯度变化表征边缘时，梯度变化较大的区域通常比较宽，所以利用x和y方向的梯度确定一个法向arctan(y/x)，然后在法向上判断当前梯度测量是否是一个峰值（或局部极大值），如果是就保留，不是极大值就抑制，如图1所示。

图1 非极大值抑制示意图

在Canny算子检测焊缝中进行非极大值抑制步骤必不可少，目的就是通过梯度变化确定出图像中的局部最大值，同时将非极大值的像素值置为0，通过这种处理可以将大量的伪边缘点剔除，使得边缘检测准确可靠。

1.3 双阈值边缘假设

Canny算法不使用单一阈值滤波，而是使用一种双阈值法的连通分量分析技术[5]。此步骤使用两个阈值，T1和T2，其中T1＞T2，将像素划分为边缘和非边缘像素。梯度值高于T1的像素被归类为边缘像素，像素值处于T1和T2之间的被归类为潜在的边缘像素，T2下的像素被归类为非边缘像素，所有靠近确定边缘的潜在边缘像素也会被标记为确定边缘像素。通过判断较强的边缘像素和相对较弱的边缘像素，可以把焊缝图像中的边缘轮廓完整提取出来，在轮廓末端会在当前像素邻域内进行判断，找出大于T1值的像素，并确定为边缘像素，使得检测出图像边缘并完全闭合。

1.4 CPU执行Canny算子耗时分析

表1是对不同尺寸的图像完成整个Canny算子边缘检测的执行时间；图2是在CPU执行Canny算子的整个过程中各个步骤的所耗时间比例，Canny算子在高斯滤波和边缘搜索环节最为耗时，高斯滤波通过卷积操作对图像的每个像素进行运算，如果不进行加速，此步骤耗时严重，不过该操作很容易进行GPU并行化加速改造；同时边缘搜索是对已经被标记的8邻域点进行搜索，如果是有效点，则标记处理，该单一线程搜索模式速度缓慢，利用GPU优化也相当合适。

表1 CPU实现不同图像尺寸Canny算法的执行时间

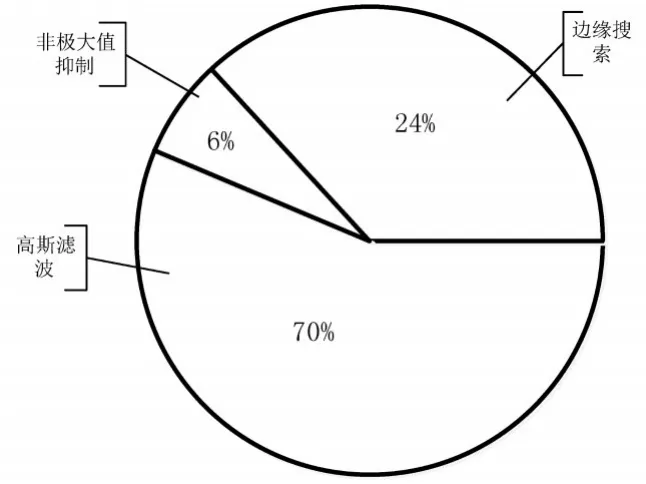
图2 Canny算法各步骤执行时间比例图

2 Canny算法优化与GPU加速

2.1 优化高斯滤波和差分

高斯滤波通过公式（4）对焊缝图像进行滤波操作：

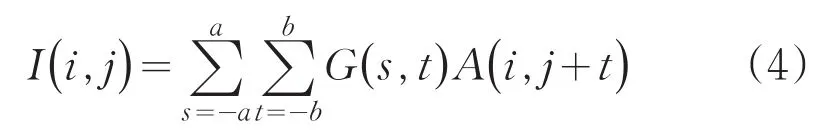
其中，I(i,j)为滤波后的像素值，A(i,j+t)为原像素值。由公式（1）和公式（2）可知高斯卷积核呈中心对称分布，可以将高斯滤波分为x方向和y方向两次滤波，各个方向均为一维高斯滤波[6]。

其中，公式（5）和公式（6）分别是是焊缝图像在x方向上和y方向上的一维高斯滤波。之前对焊缝图像像素采用二维高斯滤波改造为两次相垂直方向的两次滤波，具有两个明显的好处：首先，运算复杂度降低，对于分辨率为M×N大小的焊缝图像，原有的复杂度O((2a+1)×(2a+1)×M×N)降为O((2a+1)×M×N×2)；还符合GPU并行处理模式，将单一线程操作扩展为多线程并行操作，利用GPU的多线程并行处理优势极大缩短了焊缝图像的高斯滤波时间，GPU加速原理如图3所示。

图3 GPU加速原理图

2.2 GPU加速非极大值抑制和双阈值图像分割

非极大值抑制在Canny算子整个算法流程中所用时间最少，该步骤和双阈值图像分割过程一样均属于大数据量简单计算操作，根据寻找搜索方向和梯度大小，判断所寻找到的像素点是否为局部最大值，决定该处灰度值是否置为0。利用图3所示的GPU并行加速方法，只要得到搜索方向和梯度大小就可以进行快速的迭代比较，完成非极大值抑制和双阈值图像分割[7-9]。

2.3 优化边缘搜索

GPU线程通信有线程同步、共享存储器和原子操作三种方式，对于同一个Block中的线程才可以直接实现通信，而不同Block中的线程不能通过共享内存、同步的方式进行通信，所以即使在GPU上完成边缘连接的操作，还需要将GPU显存中的数据传回内存以完成各个线程的同步，这个数据传输过程是极其耗时的，甚至大于边缘连接的时间；如果采用原子或主机介入的方式，会出现边缘像素位置不连续的问题，同时数据也会出现明显的延迟，非常不利于速度的提升[10-12]。

因此，考虑使用先进先出（FIFO）来完成强边缘图像S(i,j)中所有像素边缘的连接[13]。在强边缘图像S(i,j)中，第一像素P被推入队列中，并且同时以P点作为起点，弱边缘图像W(i,j)搜索P点的八邻域，如果弱边缘像素存在，它们被添加到强边缘图像S(i,j)中，同时也被压入到队列的尾部，从队列的头部提取已被分类为强边缘Q点，再以Q点为起点，继续搜索弱边缘图像W(i,j)中Q点的8邻域像素，如果周围没有弱边缘像素，则直接从队列中删除，并对其他像素重复上述过程，直到队列为空。然后将S(i,j)中的第二个像素压入队列，重复上述过程，直到S(i,j)的每个像素都被搜索到为止。图4显示了起点P(3 ,2)的边缘连接。

图4 边缘连接示意图

3 实验结果和讨论

实验环境如表2所示，对于1280×960像素大小的图片，不同方式的边缘检测结果如图5所示，图5（b）为CPU边缘检测效果图，图5（c）为OpenCV处理效果图，图5（d）为GPU+CPU的效果图与上述两种处理方式结果基本一致。

表2 实验环境

图5 不同处理方法的效果对比图

由图5看出原始Canny算法和优化加速后的算法效果基本一致，焊缝轮廓已经能够很好地与背景分割开，不影响焊缝图像后续的霍夫检测等处理，上述实验说明本文算法可行。

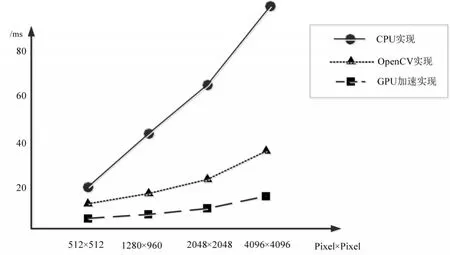
图6 不同实现方法速度对比图

针对不同版本的Canny检测算法的实验结果如图6。图6是GPU加速实现、OpenCV实现、单一CPU实现的检测结果。从图中可以看出，对于不同尺寸的图像，使用GPU并行计算的执行速度较其他算法有明显提高。通过表3数据可以看出：由于Canny算子使用了GPU多线程并行处理的方法，相比单一CPU实现和OpenCV实现速度都有明显的提升，并且对于像素数越大的图像这种加速效果越明显。因此，在实际的焊缝图像检测中，可以选择CPU+GPU的计算模式进行更高效率的焊缝检测。

表3 不同像素尺寸焊缝图像各种实现方法速度对比

4 结论

本论文对Canny算法流程的各个步骤都进行了GPU并行化改造优化，使得Canny算子对焊缝边缘检测的速度大幅度提升，可以将1280×960像素大小的焊缝图像边缘检测时间缩短到10ms以内，既满足了快速的工程实用性要求，检测结果也满足焊缝图像的后期处理要求。此外，GPU拥有强大的计算能力，适宜大数据量并行化处理，同时价格亲民、性价比突出，对Canny算法具有较好的灵活性和较快的计算速度，对焊缝边缘快速检测具有重要意义。