新型泥石流柔性防护体系冲击动力响应分析
2018-10-31王秀丽冉永红杜媛媛
王秀丽, 乔 芬,冉永红, 杜媛媛
(1.兰州理工大学土木工程学院,甘肃 兰州 730050;2.西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州 730050)
工程措施是治理泥石流最主要也最有效的措施之一,其中拦挡坝最为常见,拦挡坝有重力式实体拦挡坝和格栅坝。我国对拦挡坝的研究已有一系列的成果,吴玮江等[11]规范了其稳定性计算公式并得到实践证明。刘建兵等[12]在原有格栅坝类型的基础上提出了新型悬挑式泥石流网格格栅坝。但重力式实体坝和刚性格栅坝刚性较大发生撞击的时候时间非常短,时间越短冲击力越大,对坝体的破坏性越大。柔性防护体系在国外研究已久但在国内时间尚短,也有一些成果,赵世春等[13]研究了被动柔性防护网受力机理并进行了实验研究和数值计算。但国内关于柔性防护系统在泥石流上的研究和应用较少,因此提出泥石流新型柔性防护体系,其冲击时接触时间增长可以大大减小对坝体的伤害,延长坝体的寿命,且新型防护体系具有很强的透水性,泥石流被拦挡的过程有脱水作用,可减少流体冲击的作用。
1 有限元分析模型
泥石流柔性防护体系结构类型的选择主要由泥石流沟道宽度决定,当沟道宽度不大于12 m时选用VX型,当大于12 m时选用UX型。两者的区别在于UX型防护体系中间带有钢柱,VX型没有[14-15]。
参考舟曲泥石流灾后治理的相关资料,建立如图1所示的防护体系模型,模型的总高度为6 500 mm,横向钢索最长为11 500 mm,最短为8 750 mm,图1尺寸标注为工况1的尺寸为例,网格尺寸0.7 m其他工况只是网格尺寸不同。表1为冲击工况表说明不同工况所用冲击物直径、速度和钢筋网的钢筋直径、网格尺寸及钢筋材料情况。
运用ANSYS/LS-DYNA按照模型尺寸建立模型,柔性防护体系采用BEAM161单元,冲击物采用SOLID165单元[16-17]。防护体系模型采用塑性随动模型(Plastic Kinematic Model),该模型各向同性、随动硬化或各向同性和随动硬化的混合模型,考虑了材料的塑性应变影响。弹性模量2.06×105MPa,密度7 850 kg/m3,泊松比0.3,切线模量为600 MPa,失效应变0.2,钢材Q345屈服强度335 MPa。模拟过程冲击物为泥石流中的大石块,不考虑冲击物的变形,冲击物的本构模型采用刚体模型,密度2 600 kg/m3,弹性模量3×104MPa,泊松比0.27,这样可以减少计算所需时间,还可以简化计算过程中出现的其他问题,使所研究的防护体系成为关键所在。
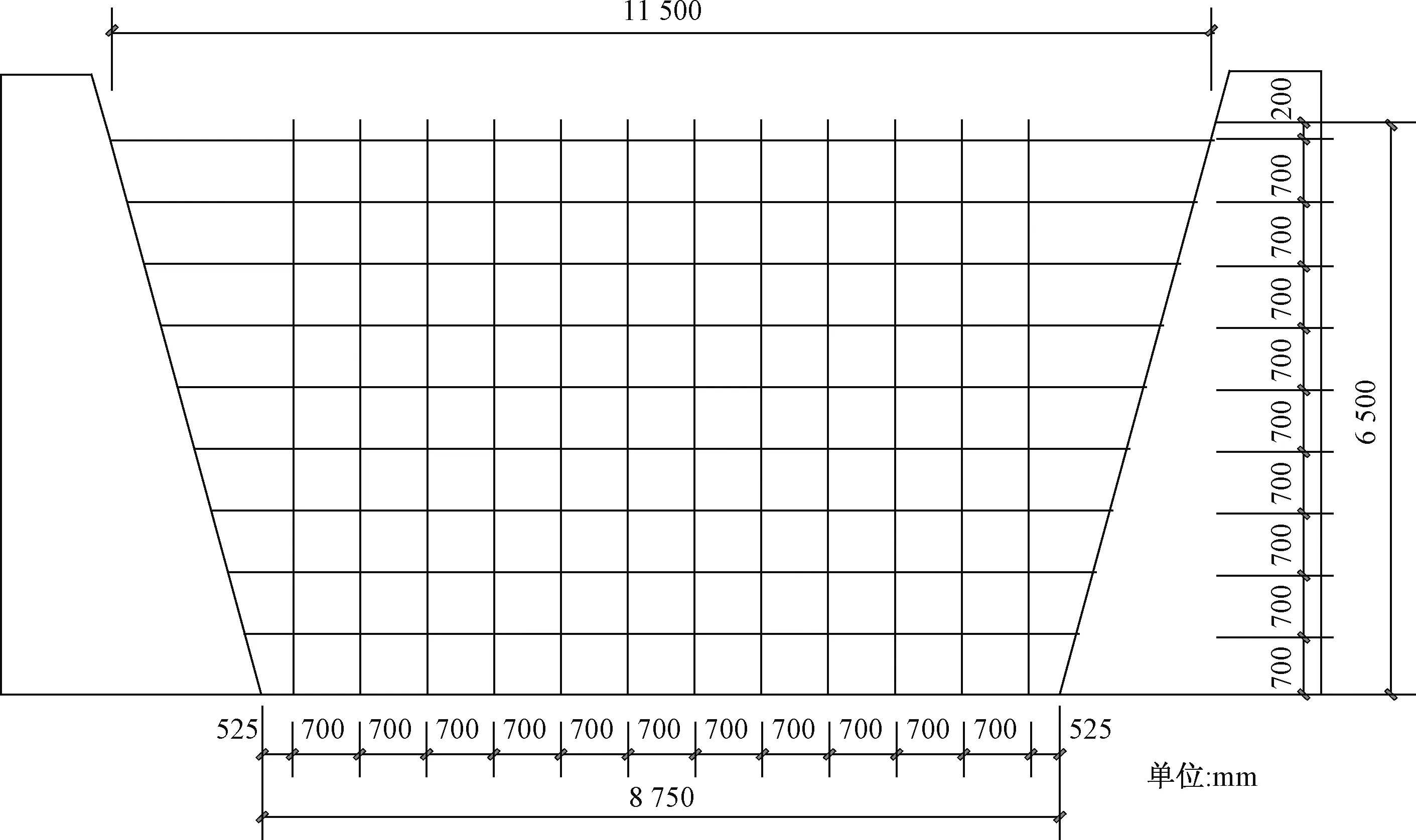
图1 防护体系模型图Fig.1 Protection system model diagram
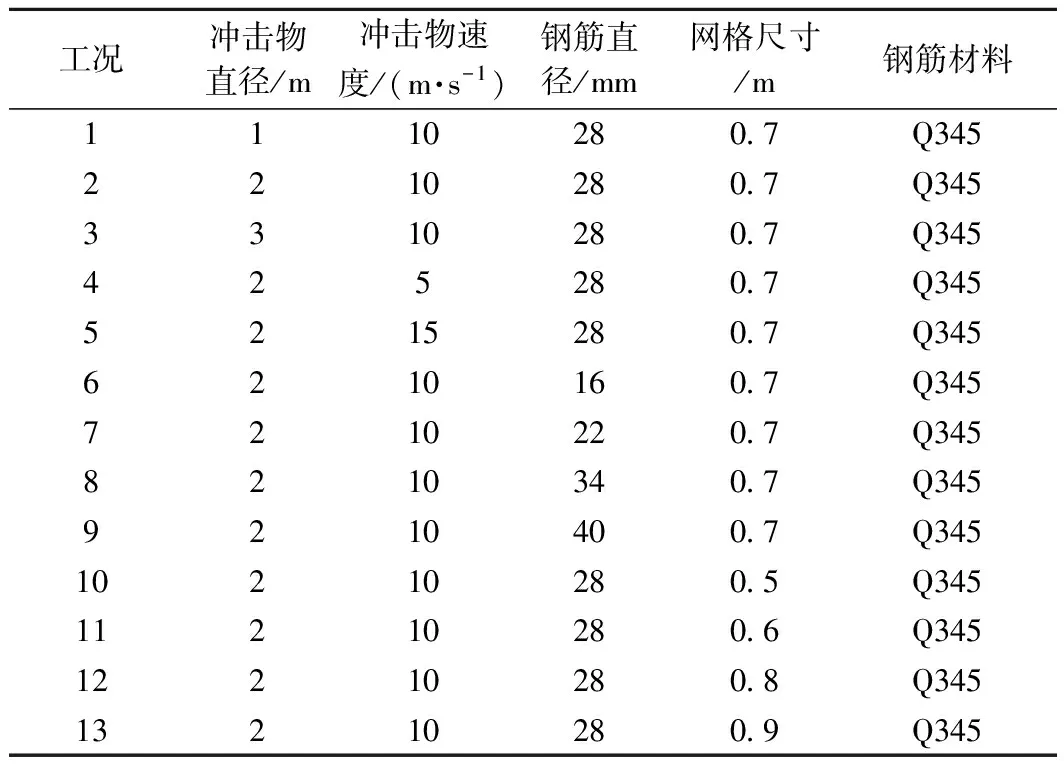
表1 冲击工况表Table 1 Impact condition table
2 索网体系破坏模式
防护体系的破坏模式可以归纳为以下几种:
(1)体系竖向钢索断裂一根然后横向断裂直至整个撞击物从体系中间穿出去。其中在直径为2 m的冲击物以速度为10 m/s的速度冲击直径为16 mm的新型柔性防护体系时,发生此类破坏。破裂前撞击位置的竖向钢索单元最大应力值达到679.154 MPa,横索断裂单元最大应力值达到692.822 MPa(图2)。其塑性应变值达到破坏应变值0.2,结构发生失效。
(2)横向钢索断裂,将网分成两部分冲击物从中间穿过。因防护体系三面固结,上面没有固结,在撞击的过程中,虽撞击结构中间部分但撞击物可能会上移,再将上面部分横向钢索撞断球滚出去直径为22 mm的钢索构成的新型柔性防护体系,在直径为3 m速度为10 m/s的冲击物冲击下结构发生失效,总能量达到1 743 810 kJ,横向索断裂前最大应力值632.878 MPa,断裂瞬间最大应力值下降到522.323 MPa,塑性应变值达到0.2(图3)。
在新的发展阶段,有线电视的发展离不开GIS技术,在有线电视网络资源管理系统建设方面,主要涵盖物流资源、空间资源、逻辑资源等,这些是实现网络资源管理的重要前提。通过对资源的管理能够为有线电视系统提供资源规划、故障分析、资源的割接与调度等功能,利用辅助设计对光缆网与电缆网进行规划,完善管理措施,使有线电视网络资源的管理功能与基础网络设计得到飞速发展。在有线电视网络资源管理系统建设中,要注重机房设备的建设,充分利用GIS技术,促进设计和管理系统之间的协调发展,为网络资源管理的动态化发展打下坚实的基础。
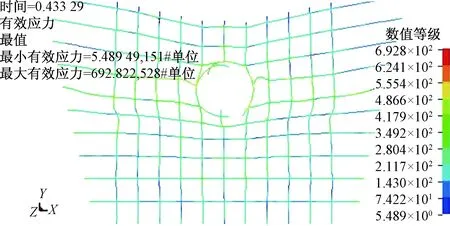
图2 体系破坏形式一Fig.2 System failure form 1

图3 体系破坏形式二Fig.3 System failure form 2
3 计算结果及分析
对防护体系冲击物参数和结构参数分别进行分析,其中冲击物参数包括质量和速度,结构参数包括防护体系的钢索直径、网格尺寸和材料强度,分析冲击力、能量、位移及应力变塑性应变等在不同参数下的变化。
3.1 不同冲击物质量下防护体系结果
3.1.1体系冲击力
工况1、2、3产生的冲击力时程曲线见图4,表2为三种工况的冲击力峰值和接触时间。由图2可以看出随着冲击物直径的增加,冲击力增大。撞击开始,三种工况的冲击力均随时间增大迅速增大到最大值然后下降,但冲击物直径越大冲击力增长的速度越快,冲击时间增长。最大冲击力工况2为工况1约4.08倍,工况3为工况2约2.28倍。说明随着冲击物直径增大冲击力增大的过程中,冲击力增大但增大的幅度减小。冲击力时程曲线为单峰值曲线,发生时间均不足1s,且随着冲击物直径增大接触时间增长。由以上分析可知:随着冲击物直径的增加,冲击力增大但增大的幅度减小;冲击力时间增大。
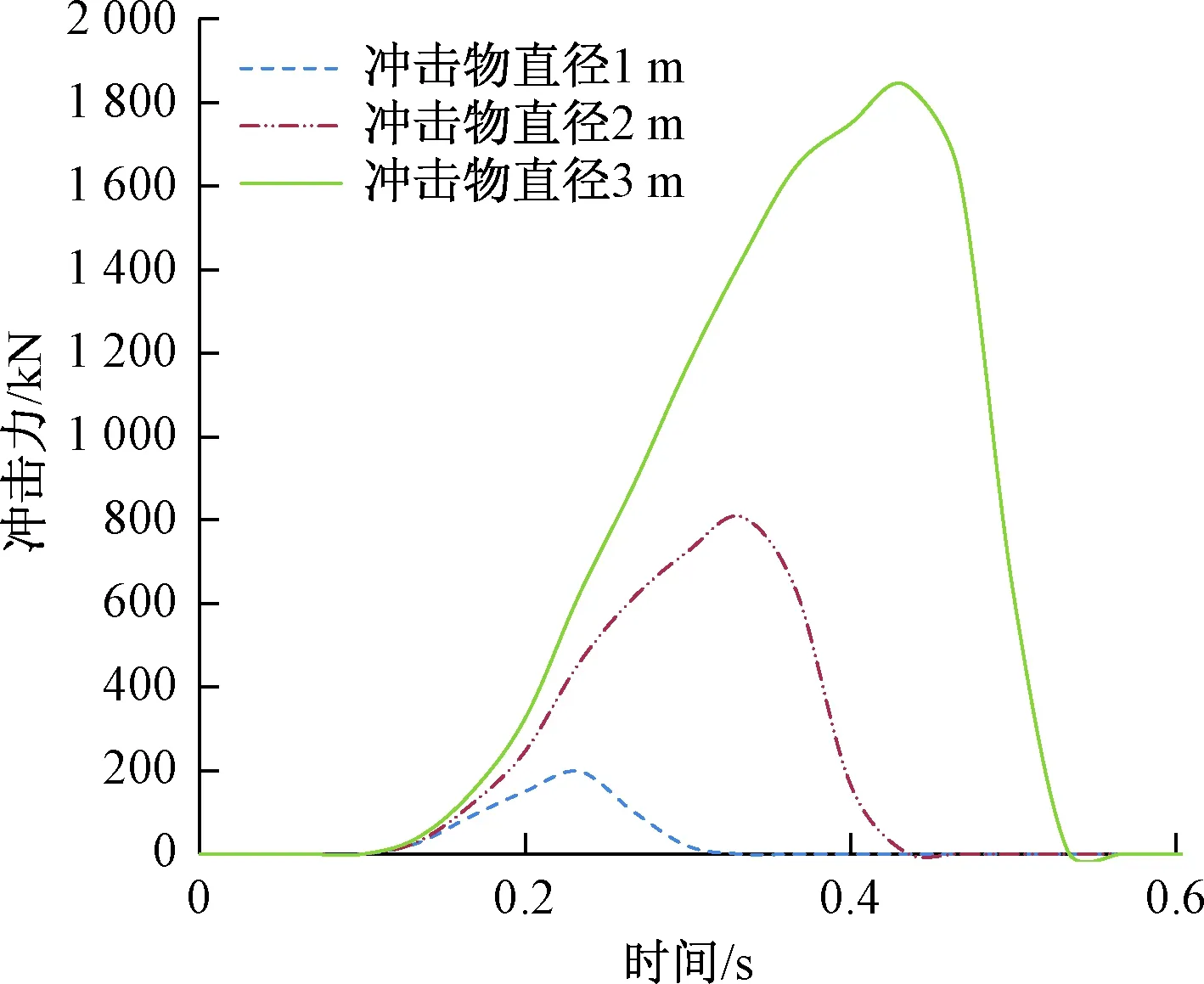
图4 冲击力时程曲线Fig.4 Impact force-time curve

表2 冲击力峰值与接触时间Table 2 The peak impact force and contact time
3.1.2体系能量
通过能量时程曲线,比较不同冲击物直径冲击下结构能量变化效果。三种工况的能量时程曲线变化趋势大致相同,总能量守恒不变,在冲击力作用下冲击物的动能从最大值即总能量值迅速下降到最小值在稍有增加达到一个稳定值,对应的体系内能从零开始突然增加到最大值,当增加到最大数值后稍微下降到一个稳定值保持不变,可以看出冲击物的动能大部分转化为防护体系的内能,图5为其中工况1能量时程曲线。工况1转化为内能效率为76.9%,工况2转化为内能的效率为95.3%,工况3转化为内能的效率为97.4%。可见工况3总能量最大且转化为能内的效率最高。由于上分析可得:随着冲击物直径的增大,冲击物总质量增加,冲击结构的总增量增大,转化为内能的效率增大,但增大的幅度减小。
3.1.3体系位移
抗冲击性能的重要指标之一就是位移,冲击荷载下冲击方向位移不能过大否则防护体系就会发生局部破坏,对冲击物的拦挡作用大大减小。撞击时,防护体系受外力作用产生了速度和加速度,自身发生变形,当速度减小到为零时,撞击方向位移达到最大。在冲击物的冲击下取撞击位置的相同节点,三种工况的位移时程曲线见图6。有曲线可知三种工况位移时程曲线变化规律大致相同即随时间的增大上升,但工况2、3位移达到最大之后稍有下降最终达到稳定,工况1位移的波动明显,三种工况位移增加的速度相同达到最大位移的时间不同。其中工况1最后位移稳定值为498.852 mm,工况2的稳定值为1 430.31 mm,工况3的稳定值为2 142.37 mm。由以上分析可知:随着冲击物直径的增加,结构达到最大位移的时间增长,最终达到稳定的位移值增大,且位移的波动减小。
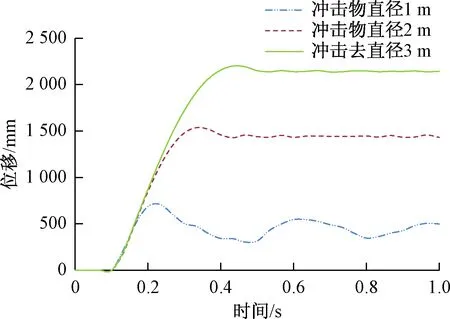
图6 位移时程曲线Fig.6 Displacement-time curve
3.2 不同冲击速度时防护体系计算结果
3.2.1体系冲击力
工况4、2、5冲击力时程曲线见图7。从曲线可以看出:工况4速度最小即5 m/s,冲击开始的时间最迟,发生冲击接触的时间为0.4 s,最大冲击力为324.504 kN。工况2速度10 m/s,接触的时间为0.3 s,最大冲击力为807.79 kN。工况5的冲击物速度最大15 m/s,冲击开始的时间最快,接触时间为0.27 s,最大冲击力914.846 kN。三种工况发生的时间均很短,冲击力从开始到结束都不足1s,冲击力曲线为单峰值。分析可得:冲击物速度越大,最大冲击力越大,冲击力发生的时间越短。
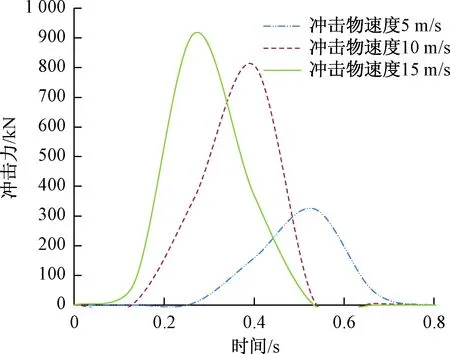
图7 冲击力时程曲线Fig.7 Impact force-time curve
3.2.2体系能量
三种工况的能量时程曲线变化趋势基本与工况1图5相同。工况4总能量为131 667 kJ,最终内能为113 266 kJ,内能转化率为86%;工况2总能量为526 667 kJ,最终内能为502 082 kJ,内能转化率为95.3%;工况5总能量为1 185 000 kJ,最终内能为1 153 140 kJ,内能转化率为97.3%。工况4到工况5开始发生能量转化的时间越来越短,且能量转化的时间越来越短。由以上的分析可得:冲击物速度越大,总能量越大且转化为内能的效率越高,能量发生转化的速度越快。
3.2.3体系位移
图8为三种工况的位移时程曲线。工况4位移曲线波动大,随着冲击物速度增加位移曲线波动减小,这是因为冲击能量越小结构的自由,位移达到最大位移时速率增大。工况4、2、5的最大位移分别为887.683 mm、1 430.31 mm、1 931.61 mm.可见随冲击物速度增加,钢筋网结构的最大位移增大,达到最大位移所需时间减少。
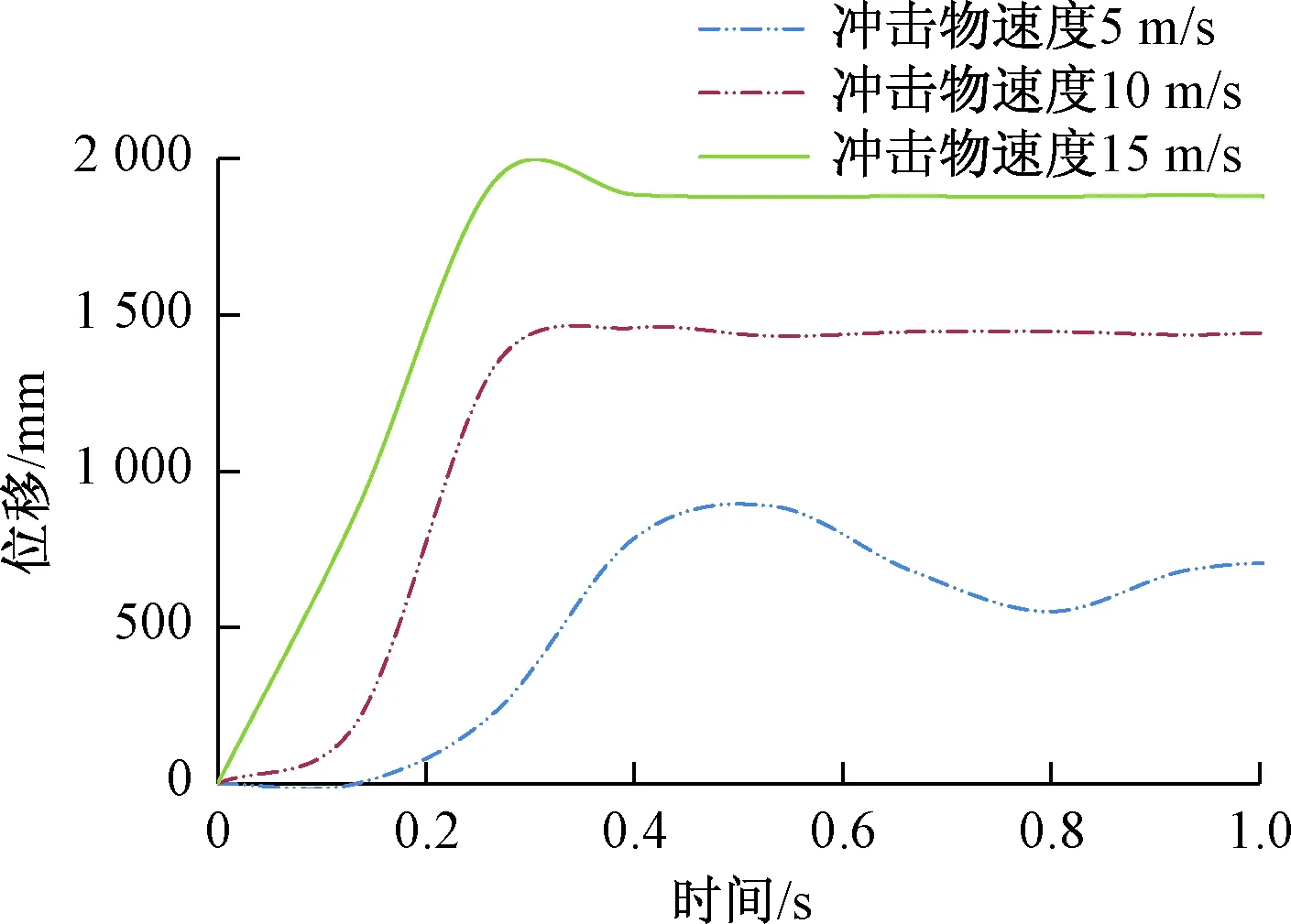
图8 位移时程曲线Fig.8 Displacement-time curve
3.3 钢索不同直径下动力响应分析
3.3.1体系冲击力
工况6、7、2、8、9,在相同的冲击物冲击作用下的冲击时程曲线见图9,冲击发生后冲击力立刻增加到最大值然后下降。工况6最大冲击力为404.619 kN,接触时间为0.73 s;工况7最大冲击力为641.507 kN,接触时间为0.37 s;工况2最大冲击力为807.79 kN,接触的时间为0.3 s;工况8最大冲击力为915.382 kN,接触时间为0.27 s;工况9最大冲击力为1 007.44 kN,接触时间为0.23 s。分析可得:钢筋直径越大,冲击力越大,冲击发生时接触时间越短,且冲击力增长速度快。
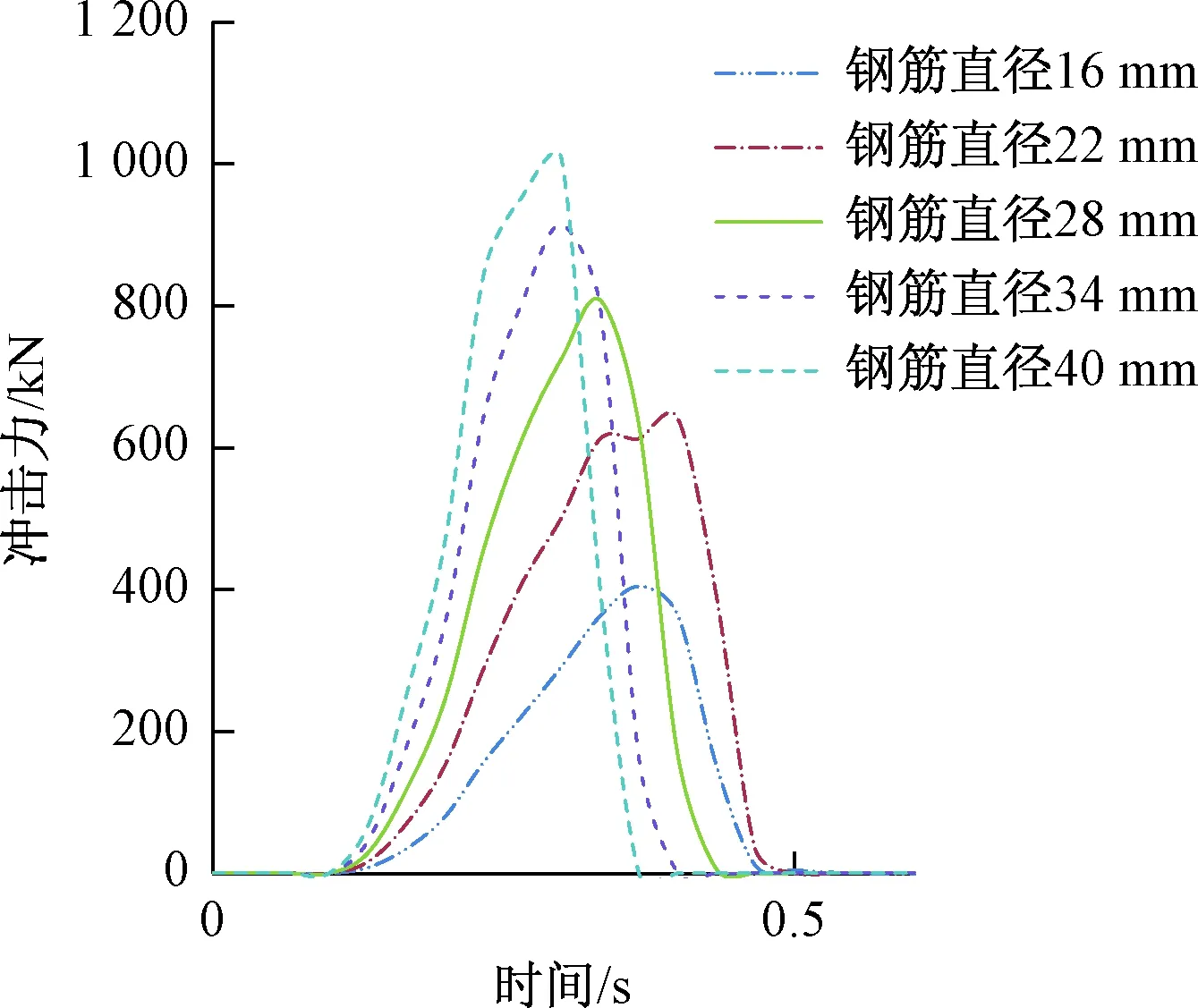
图9 冲击力时程曲线Fig.9 Impact force-time curve
3.3.2体系能量
五种工况的总的冲击能相同均为526 667 kJ,图10为五种工况的内能时程曲线。内能曲线变化基本相同,随时间增大增加达到最大值稍有下降达到稳定值,其中工况6因结构失效内能直接达到最大值即稳定值没有下降的阶段,且直径越大内能变化速度越快。五种工况转化为内能的效率为88.4%、96.2%、95.3%、93.8%、92.1%.可见除了防护体系失效的情况,随钢筋直径增加,动能转化为内能的效率下降,但转化速度增加。
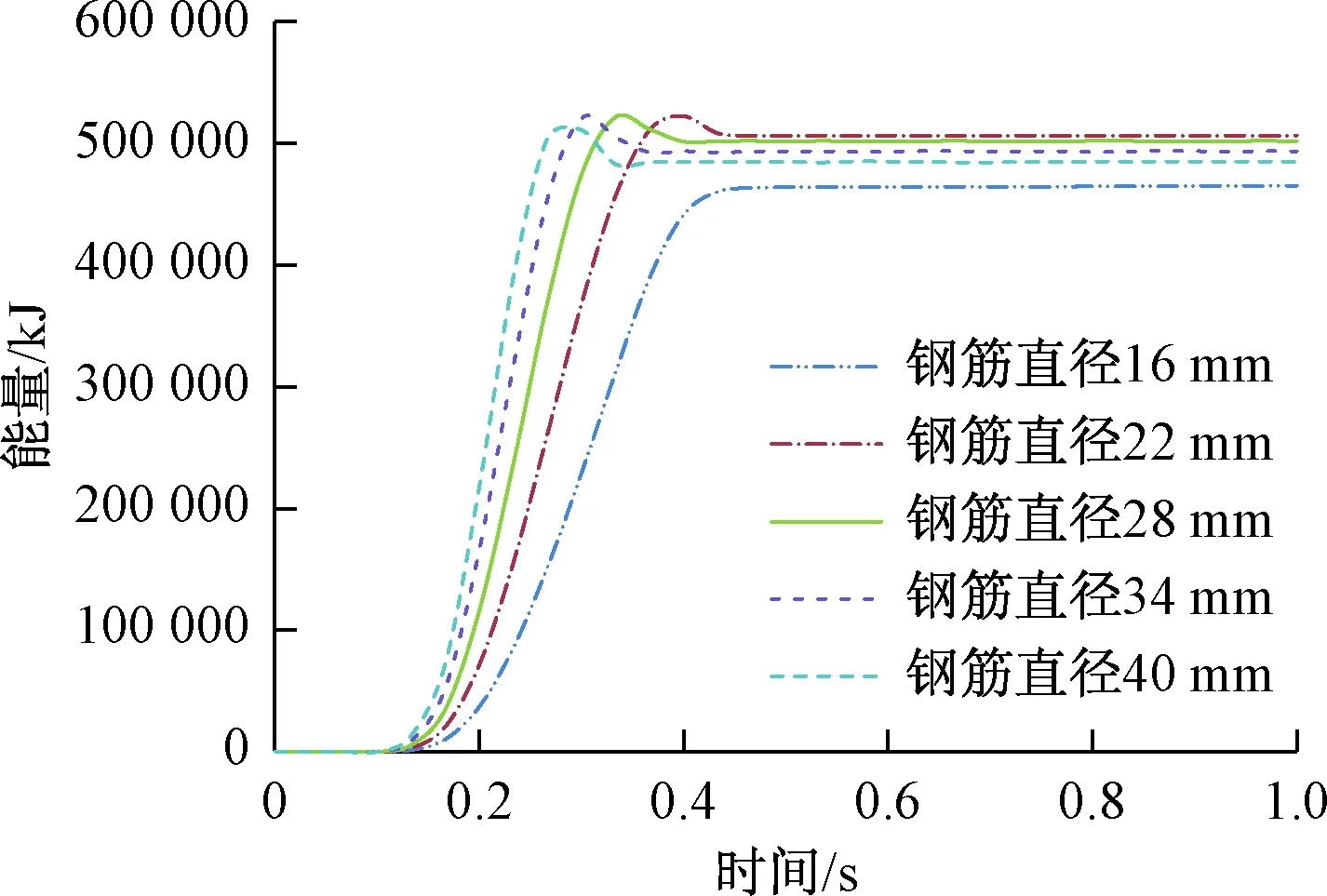
图10 内能时程曲线Fig.10 Internal energy-time curve
3.3.3体系位移
钢筋直径不同,致使防护体系的刚度不同,在冲击方向上的位移表现不同,结构通过位移增大来达到能量的消耗。图11为不同工况的位移时程曲线。由图11可明显看出五种工况位移增加的速度相同但达到最大位移的时间不同,曲线变化基本相同,位移从零增到最大值然后位移稍有下降达到稳定值。工况5因体系已发生破坏,位移在达到最大值后没有下降。最终位移依次是2 254.43 mm、1 767.5 mm、1 430.31 mm、1 213.75 mm、1 025.26 mm。分析可得钢筋直径越大,位移越小,但位移减小的程度减小。
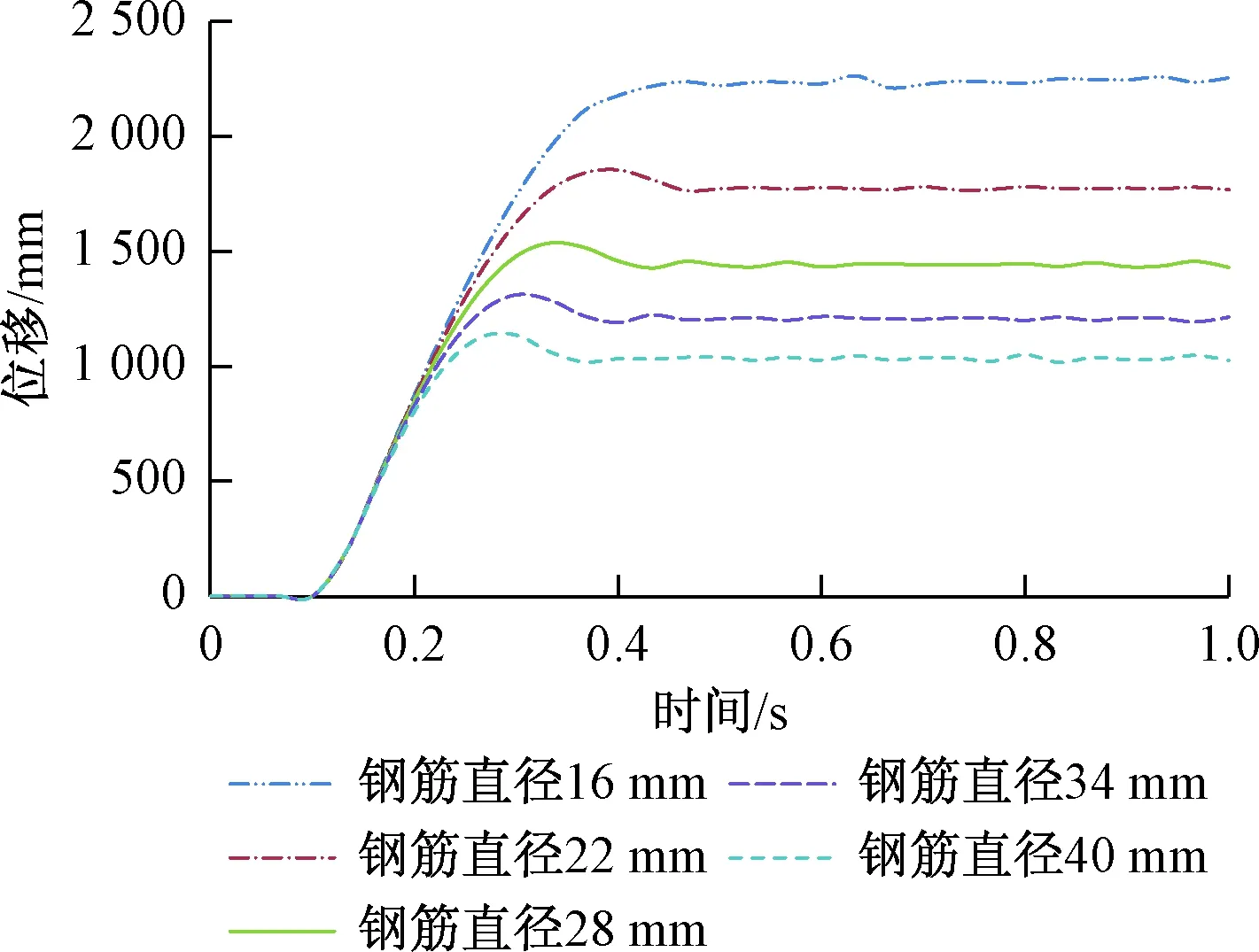
图11 位移时程曲线Fig.11 Displacement-time curve
3.3.4体系应力、应变
五种结构的最大应力值随钢筋直径变化曲线见图12,可以看到随着钢筋直径增大应力值下降再上升,在直径34 mm时,应力值达到最小。塑性应变直径16 mm的为0.2,达到失效应变,从塑性应变时程曲线图13看出曲线随时间变化基本相同,刚开始增大达到有一个短暂的平稳再继续增大最终达到稳定值。直径大的结构塑性应变变化速度快,平稳值后速度发生变化转化钢筋直径小的增长速度快,最终钢筋直径34 mm的结构的塑性应变最小。
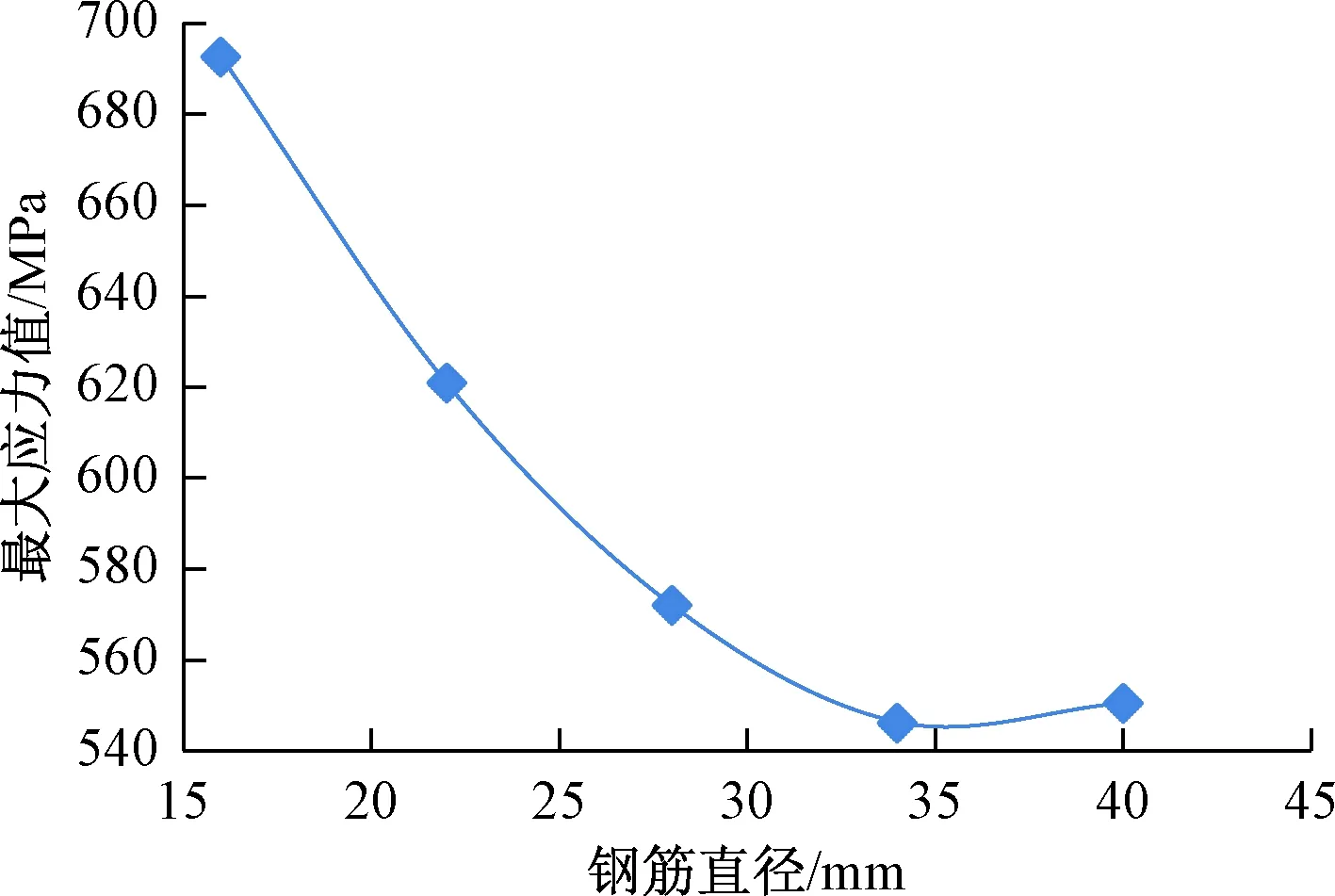
图12 最大应力随钢筋直径变化曲线Fig.12 The maximum stress varies with the diameter of the steel bar
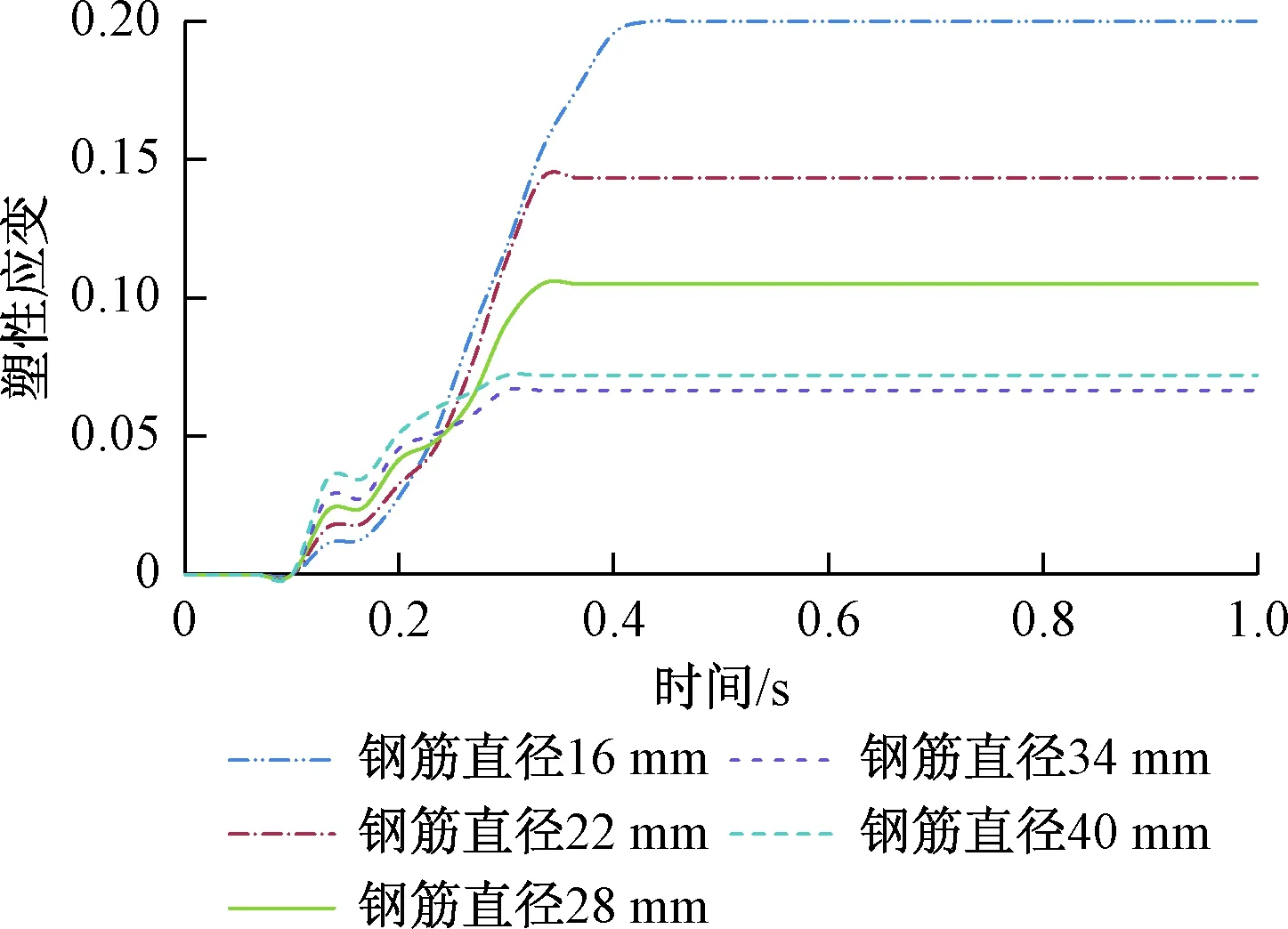
图13 塑性应变时程曲线Fig.13 Plastic strain-time curve
3.4 体系不同网格尺寸下动力响应分析
3.4.1体系冲击力
图14为不同网格尺寸的冲击力时程曲线。从曲线可以看出:工况的曲线趋势相同,与冲击去接触后,冲击力立刻从零达到最大值,然后冲击物离开防护体系,冲击力立刻减小到零。随着钢筋网尺寸的增加最大冲击力下降;冲击力增加过程中斜率减小即增速降低;冲击时间增长。符合公式mv=Ft,冲击时间越长,冲击力越小。其中冲击力峰值分别为:936.7 kN、872.612 kN、807.79 kN、750.013 kN、715.667 kN。分析得出随着钢筋网防护体系网格尺寸的增加,冲击力峰值越来越小,冲击时间增长。
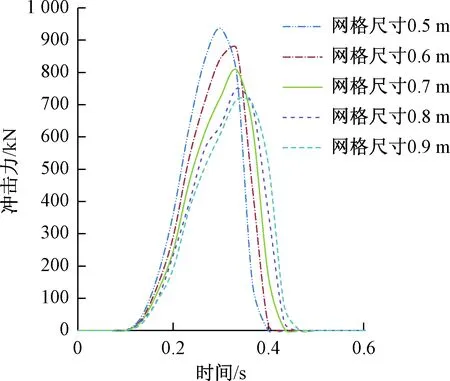
图14 冲击力时程曲线Fig.14 Impact force-time curve
3.4.2体系能量
在冲击物撞击钢筋网体系全过程中,忽略能量的热耗散,体系总能量一直守恒,动能与内能变化成对称形式,动能减小内能增加最后能量趋于稳定,且5种工况的总能量均为526 723 kJ。图15为五种网格尺寸内能随时间变化曲线。可以看出:随时间增加内能增减,刚开始增加速度慢然后增加速度增大,当达到最大能量值后稍有下降能量达到稳定值,五种工况的变化规律相同,但间隔0.5 m的钢筋网能量变化速度最快,间隔0.9 m钢钢网能量变化最慢,即网格间距越小能量达到最大值时间越小。这表明与冲击物接触的钢筋根数越少,体系能量转化速度慢,吸收的能量多。能量最终转化为内能的效率分别为93.76%、94.4%、95.3%、95.65%、95.69%。可见动能转化为内能的效率越来越多,但变化不大。
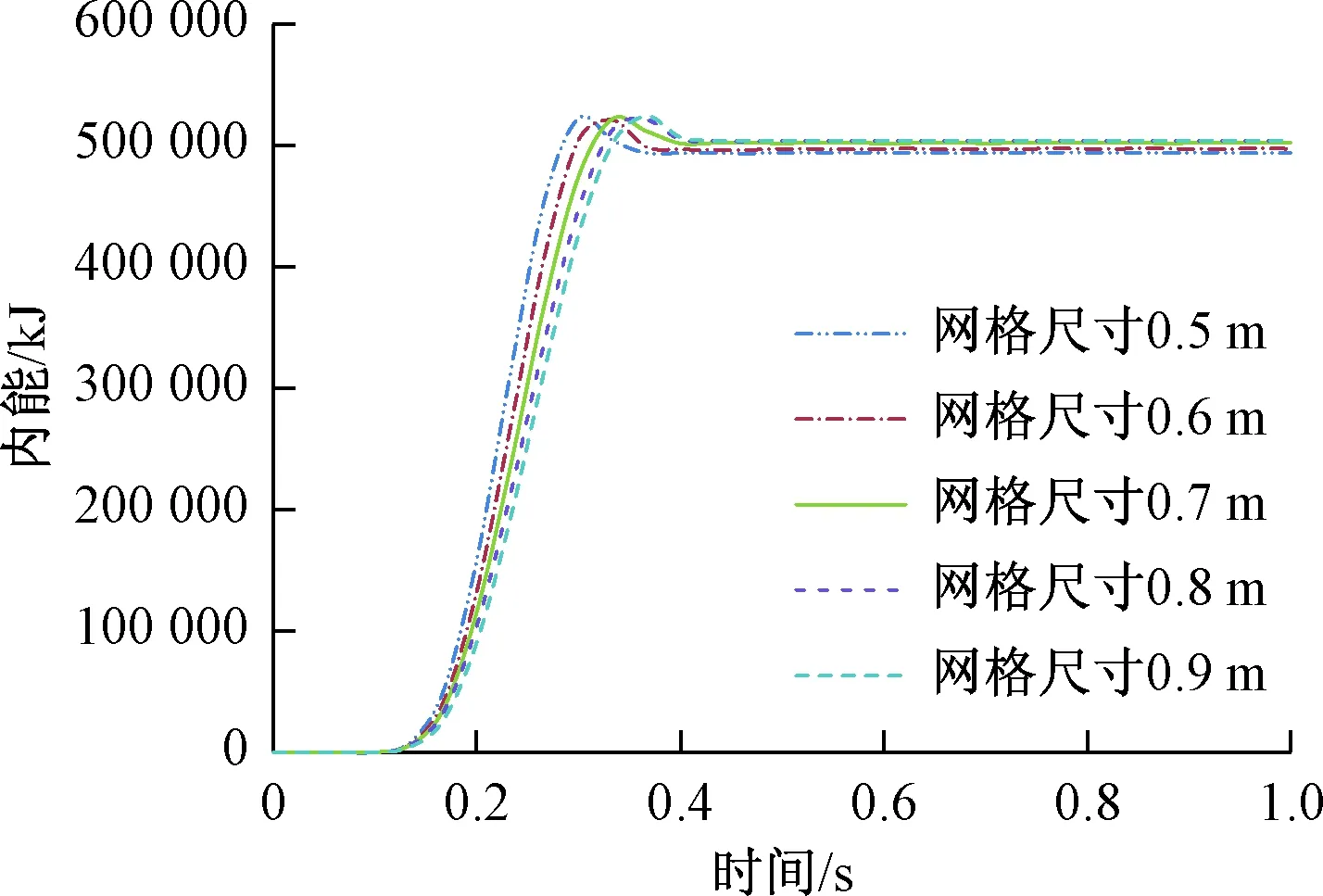
图15 内能时程曲线Fig.15 Internal energy-time curve
3.4.3体系位移
新型柔性防护体系的耗能原理是通过自身产生大变形来吸收初始的大部分动能。变形的形式表现为在撞击方向上的位移。图16为五种不同间隔的钢筋网位移时程曲线。从曲线可以看出:随着钢筋网网格尺寸变大,冲击物与防护体系接触冲击时间逐渐增长;曲线上升达到最大位移时间增长,位移增长的速率基本相同;位移随时间增大到最大值然后稍有下降达到定值,位移增大的幅度减小。可见网格尺寸增大最终位移增大,位移增长幅度减小。
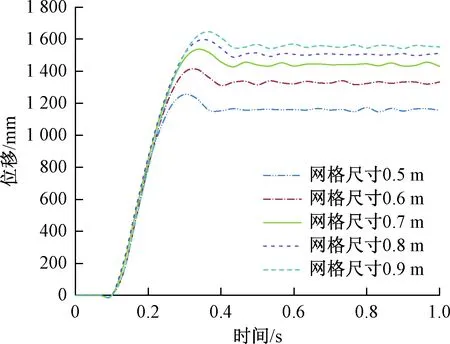
图16 冲击点处位移时程曲线Fig.16 The displacement curve at the impact point
3.4.4体系的应力、塑性应变
根据应力云图提取五种工况的最大应力值,得到最大应力值随网格尺寸变化曲线见图17,可以看出随着网格尺寸增大最大应力值下降,再稍有增加,网格尺寸0.8 m的钢筋网最大应力值为五种网格中最小。图18为不同网格尺寸塑性应变时程曲线,均为达到失效应变0.2,结构未发生失效。从曲线可以看出,随时间增加,塑性应变值迅速增加,然后达到最大值即稳定值。最大塑性应变值变化为,随网格尺寸增大降低再升高,其中0.8 m的网格尺寸的塑性应变值在五种工况中最小。
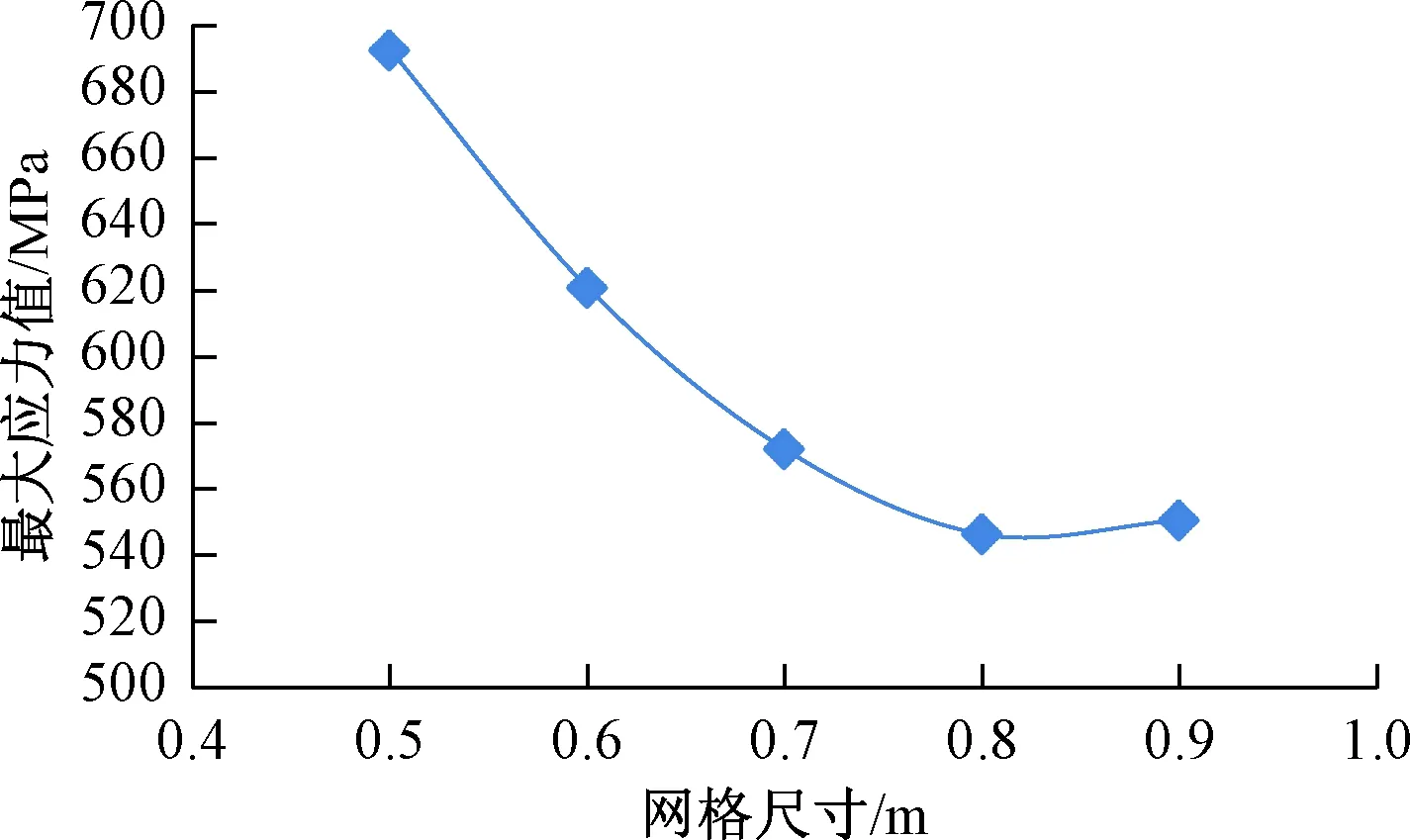
图17 最大应力随网格尺寸变化曲线Fig.17 The maximum stress varies with the mesh size
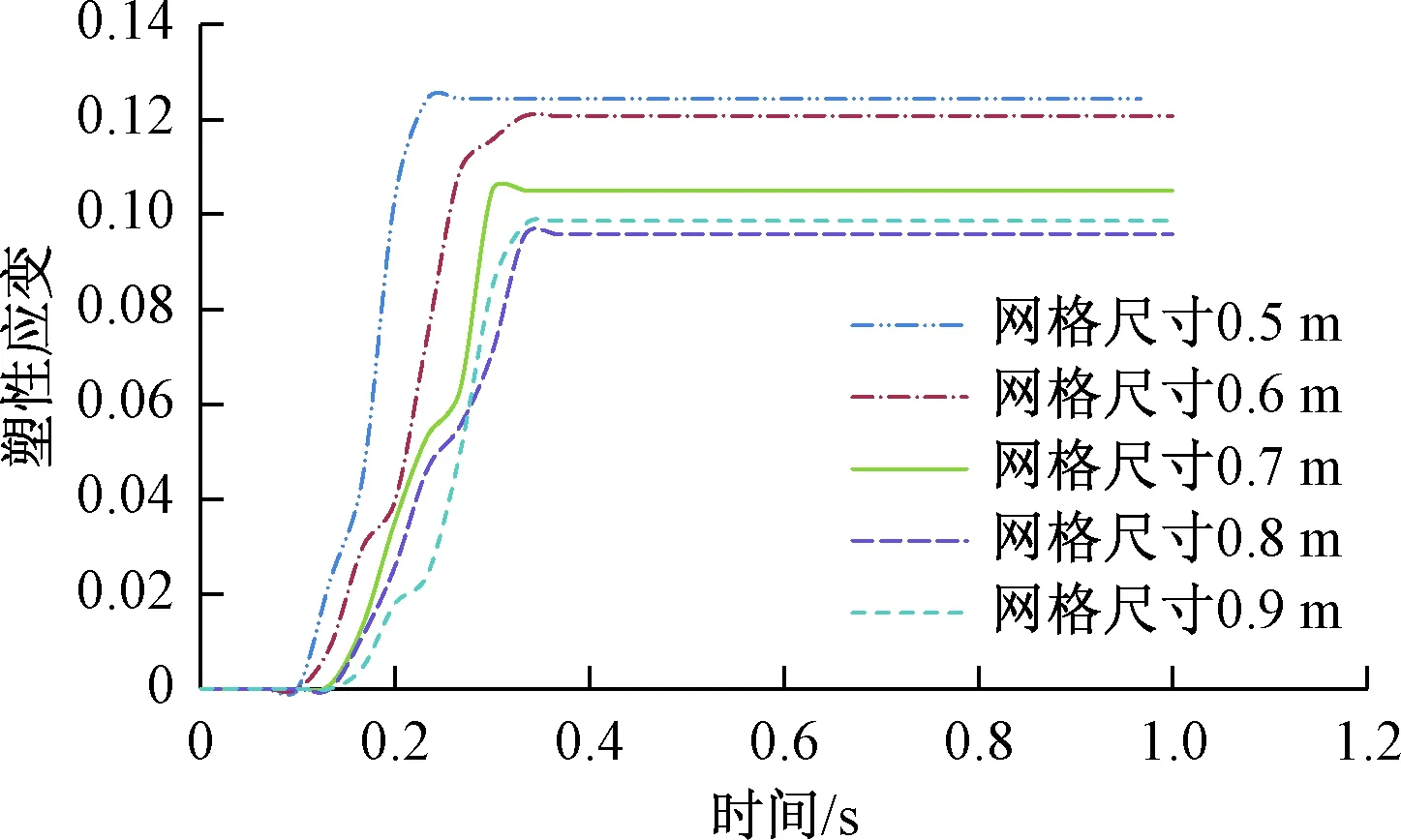
图18 塑性应变时程曲线Fig.18 Plastic strain-time curve
4 结论
运用ANSYS/LS-DYNA对新型泥石流柔性防护体系进行动态有限元分析,得到如下结论:
(1)防护体系冲击能量转化为内能的效率均比较好,说明其能较好的消耗能量,具有较强拦截大石块的能力,可以应用到实际工程当中。
(2)当冲击物直径增大2倍时冲击力增大约4倍,转化为内能的效率约增大1.2倍,位移增大约2.9倍;冲击物直径增大约3倍时,冲击力增大约4倍,转化为内能的效率约增大约1.27倍,位移增大约4.3倍。因此随冲击物直径增大冲击力、转化为内能的效率及位移增大程度减小。
(3)当冲击物速度增大2倍时,冲击力增大约2.49倍,转化为内能的效率增大约1.1倍,位移增大约1.58倍;当冲击物速度增大约3倍时,冲击力增大约2.82倍,转化为内能的效率增大约1.13倍,位移增大约2.18倍。
(4)钢索直径按6 mm为等差数列增加时,冲击力增大值不是等差数列且增大值减小;直径16 mm的柔性防护体系失效;在体系不失效的情况下,转化为内能的效率均在90%以上,且随直径增大减小百分比程度变大;位移明显降低,减少值减小;最大应力值和塑性应变变化均为先减小再增大在钢筋直径34 mm时达到最小。
(5)防护体系网格尺寸以0.1 m为等差数列增加,冲击力以不是等差数列的方式减小;转化为内能的效率在90%以上且略微增大;位移越大增大值减小;最大应力值和塑性应变随网格尺寸增加减小再增大且在网格尺寸为0.8 m时最小。
