基于平滑片段计数正则化的图像盲解卷积
2018-10-31姜小磊姚鸿勋孙晓帅
姜小磊, 姚鸿勋, 孙晓帅
(哈尔滨工业大学 计算机科学与技术学院, 哈尔滨 150001)
引言
运动模糊是一种非常常见的图像降质过程,可使得所拍摄的照片丢失大量细节信息,从而失去使用价值。随着便携电子设备的普及,人们获得清晰图像的要求也日益迫切。这使得图像盲解卷积具有不容忽视的实际重要意义,研究人员为此付出了巨大努力。图像非盲解卷积和盲解卷积的区别在于前者假定模糊核已知,而后者则需要估计出模糊核,因而是需要分别处理的2个问题。图像盲解卷积的任务主要是估计出模糊核,有了模糊核后再利用图像非盲解卷积得到最终的复原图像。当前,大多数盲解卷积方法在最大后验概率(Maximum A Posteriori (MAP))框架内通过采用合适的清晰图像先验和模糊核先验来估计模糊核。
基于MAP框架的图像盲解卷积方法利用了各种各样的对清晰图像的先验假定。最常见的是稀疏梯度先验,即假定清晰图像的差分图像是稀疏的。很多文献,包括文献[1-7]都采用了这个先验,主要区别在于数值解法不同,有的利用变量分裂技术[1-4],有的利用重加权最小二乘[5-6],还有的利用匹配追踪[7]。鉴于稀疏梯度先验只涉及直接相邻的2个像素,为了建模更高阶的相关性可以使用图像块先验。在模糊核估计中得到应用的块先验包括边缘块[8]、块自相似性[9]、归一化颜色线[10]、低秩性[11]、暗通道[12]、极值通道[13]。除了上面这些人工设计的先验之外,近年来还涌现了一些基于学习的先验。文献[14]应用了lp范数梯度先验,但这里的p允许取负值并且通过训练得到依迭代可变的参数。文献[15]利用卷积神经网络模型训练一个二分类器,该分类器能够把清晰图像和模糊图像区分开来,因而可以作为先验在MAP框架内使用。
一些模糊核估计方法在MAP的框架之外对恢复的中间隐含图像显式地提取显著边缘并抑制无关细节。文献[16]使用了双边滤波器和shock滤波器。文献[2]利用了细节梯度和结构边缘梯度的一个区别:在一个邻域内前者能够彼此抵消而后者不能。文献[8,10]首先寻找可能包含边缘的图像块,然后只在这些图像块上应用块先验。文献[17]借助卷积神经网络模型提取显著边缘并抑制小尺度细节,而后再利用l0范数梯度先验。
如上所述,许多自然图像盲解卷积方法在估计模糊核的过程中都利用了一种“非自然”的中间隐含图像[3],其中只包含显著的轮廓边缘而没有纹理细节。本文把模糊核估计的中间隐含图像与图像平滑得到的结构分量联系起来,分析比较了模糊核估计对隐含图像先验的要求和保持结构的图像平滑对结构分量的要求,在此基础上提出平滑片段计数正则项作为模糊核估计中隐含图像的先验。与显式地提取显著边缘的方法[2,8,10,16]相比,本文的方法无需借助各种启发式的中间步骤区分显著边缘与细节纹理;与其它基于计数正则化的方法[3,12-13,18]相比,所提方法采用的计数正则项可以在容许大空间范围灰度渐变的同时保持阶跃边缘,因而既有助于减少卷积数据项的误差,又保持了足够的区分模糊图像和清晰图像的判别力。
1 模糊核估计与保持结构的图像平滑
在盲图像解卷积中,已知的只有模糊图像Y,研究目的是要估计出模糊核K,再借助非盲图像解卷积技术,从模糊图像Y和已经估计出的模糊核K进一步复原出清晰图像X。从已知的模糊图像可以得到待求的模糊核需要满足的约束条件:X*K=Y,其中“*”代表卷积。当然仅仅这个约束条件不足以确定模糊核K,因为清晰图像X是未知的。为了缩小求解范围,需要引入更多的约束条件。一个直接的办法是利用自然图像的先验模型,进而求解如下问题:
(1)
其中,Jx(X)是自然图像X的先验或正则项,对越不可能出现的自然图像X,其取值越大。通过求解问题(1)来进行盲解卷积的合理性取决于自然图像先验项Jx(X)。
鉴于自然图像的先验既难于建模又不能提供与模糊图像足够充分的区分度,这里就不再使用与自然图像一致的先验项。研究考虑保持结构的图像平滑问题,也就是把自然图像X分解为结构分量S和纹理分量T之和,即:
X=S+T
(2)
其中,结构分量S主要包含显著的结构信息,例如轮廓和大尺度边缘,而纹理分量主要包含细节和噪声。对上式两边与K做卷积可得计算公式如下:
Y=X*K=S*K+T*K
(3)
因为模糊核K通常是低通滤波器,起平滑作用,而纹理分量T主要包含小尺度的高频信息,故此可以认为T*K≈0。于是就可写作如下形式:
Y≈S*K
(4)
(5)
其中,Js(S)是结构分量正则项。注意问题(5)与(1)的重要差异在于,研究避开了难于处理且对模糊图像惩罚度不够的自然图像先验项Jx(X),转而考虑结构分量先验项Js(S)。
与建模自然图像X相比,建模结构分量S要容易得多。一方面,结构分量的基本要求是应当对应于大尺度的趋势分量。另一方面,从估计模糊核的角度来看,结构分量所包含的频率分量应该足够丰富。这是因为S*K=Y的频域形式是F(S)F(K)=F(Y), 所以由F(K)q≈F(Y)q/F(S)q可知:分母的模|F(S)q|越大,F(K)q的估计精度越高,这里的下角标q用于指示某个频率分量。同时结构分量是大尺度的变化趋势,所以不会缺乏低频分量。为了保证结构分量也包含丰富充足的高频信息,应当允许结构分量中出现亮度跳变。最理想的情况是S为冲激信号,则F(K)等权值地包含所有频率成分。当然这种情况发生的可能性不大,更可能出现的是阶跃边缘,此时S也包含丰富的高频成分,因而可以从Y恢复出模糊核K的很多信息(沿边缘的方向除外,因为S在该方向只包含直流分量)。很多前人的工作都或显式、或隐含地利用阶跃边缘来恢复模糊核[8,10,16],也是为了利用阶跃边缘所包含的丰富谐波分量来提高模糊核估计的精度。综合上述2条要求,结构分量应该是分段平滑的、并包含较多的高对比度亮度跳变。
2 目标函数
2.1 模糊核估计目标函数研究
按照上面的分析,结构分量的正则项Js(S)应当既容许亮度跳变又惩罚小尺度的细节,计数正则项可以很好地匹配这一要求。设想把S分成若干片段,每个片段都不包含小尺度细节,则把惩罚施加于片段的数目即可。换句话说,通过把结构分量建模为分段平滑的,并把平滑片段的数目作为正则项。为了保证每个片段都是平滑的,最简单的假定也许是其差分为常数,即线性拟合。
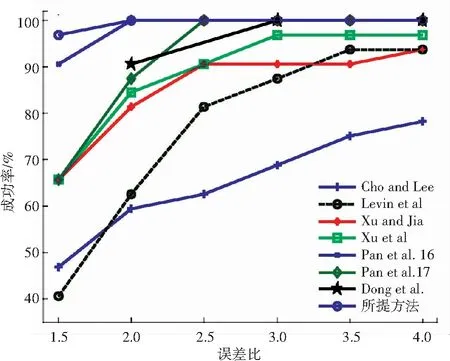
为了给出平滑片段计数正则项的定义,先引入一些记号。令x∈N。x的第i个元素记为xi,于是x=(x1,x2,...,xN)。研究把(xi,xi+1,...,xj)叫做x的一个片段,记作xi:j。假定下标i1,i2,…,iM,iM+1满足1=i1 (6) 其中,λ和α是正值参数。 把式(6)定义的正则项s(·)推广到图像,再代入式(5)可得如下估计结构分量S的目标函数的公式表述如下: (7) 其中,Θ={0°, 90°, 45°, -45°}。 这里,vec(S,n,θ)表示沿着与水平方向夹角为θ的方向扫描图像S所得的灰度值向量,此处n用于区别同一方向的不同扫描线。于是,vec(S,n, 0°)代表图像S的某一行,n用于指示不同的行;vec(S,n, 90°)代表图像S的某一列,n用于指示具体哪一列。类似可知vec(S,n, 45°)和vec(S,n, -45°)的含义。 注意对于不同的n,vec(S,n, 0°)的长度不变,vec(S,n, 90°)的长度也不变;而对于不同的n,vec(S,n, 45°)的长度可能不同,vec(S,n, -45°)也是如此。 对于运动模糊而言,模糊核K可以看作是照相机在曝光过程中相对运动路径的二维投影,因此在表示模糊核的矩阵中只有少数元素不为零。这里,就把估计模糊核的目标函数定义为: (8) (9) 式(7)和(9)完整地给出了本文方法的目标函数,应用半二次分裂法进行交替最小化,即可得到如下的模糊核估计算法。算法设计内容可参见如下。 算法1基于平滑片段计数正则化的模糊核估计 输入:模糊图像Y,隐含图像S,模糊核K,参数λ,α,η,ωλ,ωα,ωη,N 输出:模糊核K,隐含图像S,参数λ,α,η 1:forj=1 toNdo 2:βs←10-5 3: whileβs<105do 5: 通过求解(KTK+4βsI)s=KTy+βs∑θ∈Θuθ更新S 6:βs←2×βs 7: end while 8:βk←10-5 9: whileβk<105do 11: ifj≤N-2 then 13: else 14: 通过求解(STS+βkI)k=STy+βku更新K 15: end 16:βk←2×βk 17: end while 18:λ←ωλ×λ,α←ωα×α,η←ωη×η 19:end for 算法1中,第5、12、14行中的粗体大写字母代表矩阵,粗体小写字母代表列向量,其中把卷积S*K写成了Sk或Ks,y1和y2分别是y关于其第一和第二个自变量的一阶差分,S1和S2与之类似。第4行的最小化问题可以分解为若干一维子问题,并且每个子问题都可以借助动态规划算法得到准确解。第5、12、14行的线性方程组都可以利用共轭梯度法来求解。对于第10行的最小化问题,只需保留K中最大的前ηNK个元素,其余元素置零即可得到更新后的U。 文献[20]中的数据库包含4张原始清晰图片,8个模糊核,共计32张模糊图片。为了保证比较的公平性,在利用不同的方法估计出模糊核之后,研究使用文献[20]中的非盲解卷积代码来生成最后的复原图像,并利用其中定义的误差比来设置定量指标。如果把误差比小于给定数看作复原成功,那么算法相对于给定误差比r的成功率就是指误差比小于r的图片在全体图片中所占的百分数。显然,给定误差比r,对应的成功率越大说明算法性能越好。图1给出了几种方法的误差比-成功率曲线,其中方法[6]、[12]的误差比-成功率曲线来自对应文献,其它方法的结果都来自文献[18]。与文献[12]、[18]相同,研究把模糊核的尺寸设置为实际尺寸+2。如图1所示,本文提出方法的误差比-成功率曲线在其它方法的误差比-成功率曲线的上方,因而从复原清晰图像的角度来说本文提出方法估计出的模糊核更准确。 图1 几种盲解卷积方法在文献[20]中图片库上的比较 Fig.1ComparisonofseveralblinddeconvolutionmethodsonthedatasetinRef.[20] 文献[21]中的图片库包含48幅模糊图像,对应于4幅清晰图像和12个照相机运动路径。图2给出了几种去模糊算法的定量比较。其中,方法[2]、[16]的数据来自文献[21],其它方法的数据来自对应文献。图2中每个图片集的PSNR值都是对12幅模糊图像的解卷积结果的平均值,这些模糊图像对应的清晰图片是一致的。需要指出的是,图2中列出的不同文献所使用的非盲解卷积方法不一定相同,这里和文献[12]、[18]保持一致,都使用了文献[22]提供的非盲图像解卷积代码。本文提出算法中的参数ηt=0.1。 图3~5给出了几种方法对3幅模糊图像的复原效果,估计出的模糊核示于复原图像的右下角或最右一列。可以看到,与其它方法相比,本文提出方法在复原出相当的细节信息的同时没有引入过多的振铃假象。 图2 几种盲解卷积方法在文献[21]中图片库上的比较 Fig.2ComparisonofseveralblinddeconvolutionmethodsonthedatasetinRef. [21] 图3 几种盲解卷积方法对文献[21]中模糊图片库的一幅图像的复原效果 图4几种盲解卷积方法对文献[21]中模糊图片库的一幅图像的复原效果 Fig.4ComparisonofseveralblinddeconvolutionmethodsforoneimageonthedatasetinRef. [21] 图5 几种盲解卷积方法对一幅真实图像的复原效果 估计模糊核的关键在于如何建模隐含图像和模糊核。研究把隐含图像分解为结构分量和纹理分量,其中的纹理分量在模糊之后能量较小,因此建模隐含图像可以转化为建模其结构分量。在此分析的基础之上,通过对隐含图像使用平滑片段计数正则项,对模糊核使用非零计数正则项。平滑片段计数正则项对平滑片段进行计数,既可以滤除纹理细节,又可以保持对估计模糊核起重要作用的显著边缘。同时对模糊核使用的条件型非零计数正则项不会导致过于稀疏的模糊核。在对目标函数进行数值优化时,研究又应用了半二次分裂方法。对模糊图片的复原实验表明本文提出的方法不逊色于当前的其它方法。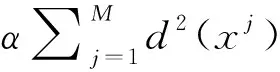

2.2 模糊核估计算法

3 实验结果



4 结束语
