基于空间位置的工业机器人干涉判断研究

赵志伟，刘振宇

(沈阳工业大学信息科学与工程学院,沈阳110870)

1 引 言

近年来，工业机器人在自动化领域受到广泛应用，其中应用最多的就是串联型六自由度机器人。这种机器人在决定位移范围时，必须考虑连杆之间的干涉问题；同时在运动过程中，也要考虑是否会和障碍物发生碰撞。国内外许多专家学者都对此问题展开研究。

方彬等人[1]曾尝试在初步检测阶段采用AABB包围盒和间隔减半来剔除场景中不相交的物体；在详细检测阶段通过对物体建立AABB来精确相交区域。Ayala等人[2]为提高检测精度，应用管状物体进行自碰撞检测。靳雁霞等人[3]曾提出融合R-Sphere包围球的碰撞检测算法，该算法首先将有公共顶点的三角片构造成包围球，利用包围球快速剔除不相交的物体，再通过粒子群算法将三维问题转换成二维问题；王鹏等人[4]利用在三角形网格中增加特征元素的信息(点、边、面)形成特征描述三角形，再结合方向包围盒OBB(Oriented bounding box)来进行碰撞检测。胡咏梅[5]提出将AABB和OBB相结合的碰撞检测算法，该算法通过对象投影来剔除不相交的物体，继而用AABB构建剩下的物体，初步判断可能相交的物体，最后用OBB来精确检测，获得了较好的实时性。

然而以上研究成果大多是将机器人杆件与障碍物当成几何多面体、椭球体或者球体。求解连杆与障碍物的距离时，为了安全起见，这些几何元件的尺寸均大于实际连杆和障碍物的尺寸，因此虽然容易做出判断，但却无法精确判断是否真正有干涉现象发生[6-10]。故此，提出一种新方法，利用工业机器人外型特征，将机器人各关节替换为更接近其形状的圆柱或圆锥体，可迅速判断出哪些连杆不发生干涉现象，并利用可能发生干涉的连杆及障碍物两者中心线的距离来判断是否真正发生干涉。所提方法不需要用到代表连杆及障碍物的几何方程，且不需要判断每一连杆与障碍物是否发生干涉，即可快速准确地判断是否有干涉发生。

2 六自由度机械臂运动学分析

2.1 建立D-H模型

以安川公司生产的六自由度点焊机器人Motoman ES165D为研究对象进行运动学建模。图1(a)即为产品实物图。该机器人结构如图1(b)所示，其运动学正解采用传统的D-H法进行描述。DH法建立各个关节坐标系如图1(c)所示(Unity3D世界坐标系中，χ-z平面为水平面，竖直方向为y轴，这里按照Unity坐标规则定义坐标系)，其中θi为连杆i与连杆i-1的夹角，αi为连杆i与连杆i-1间的扭角，ai为连杆i长度，di为连杆i与连杆i-1的距离，得到D-H参数如表1所示，第i-1坐标系与第i坐标系之间的关系可以用平移和旋转来实现。最终得到机械臂末端相对于基座上参考坐标X0-Y0-Z0的位姿矩阵T,如下式：

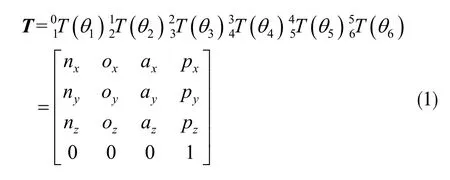
式中：nχ,ny,nz,oχ,oy,oz,aχ,ay,az为机械臂末端的姿态,pχ,py,pz为机械臂末端的位置坐标。

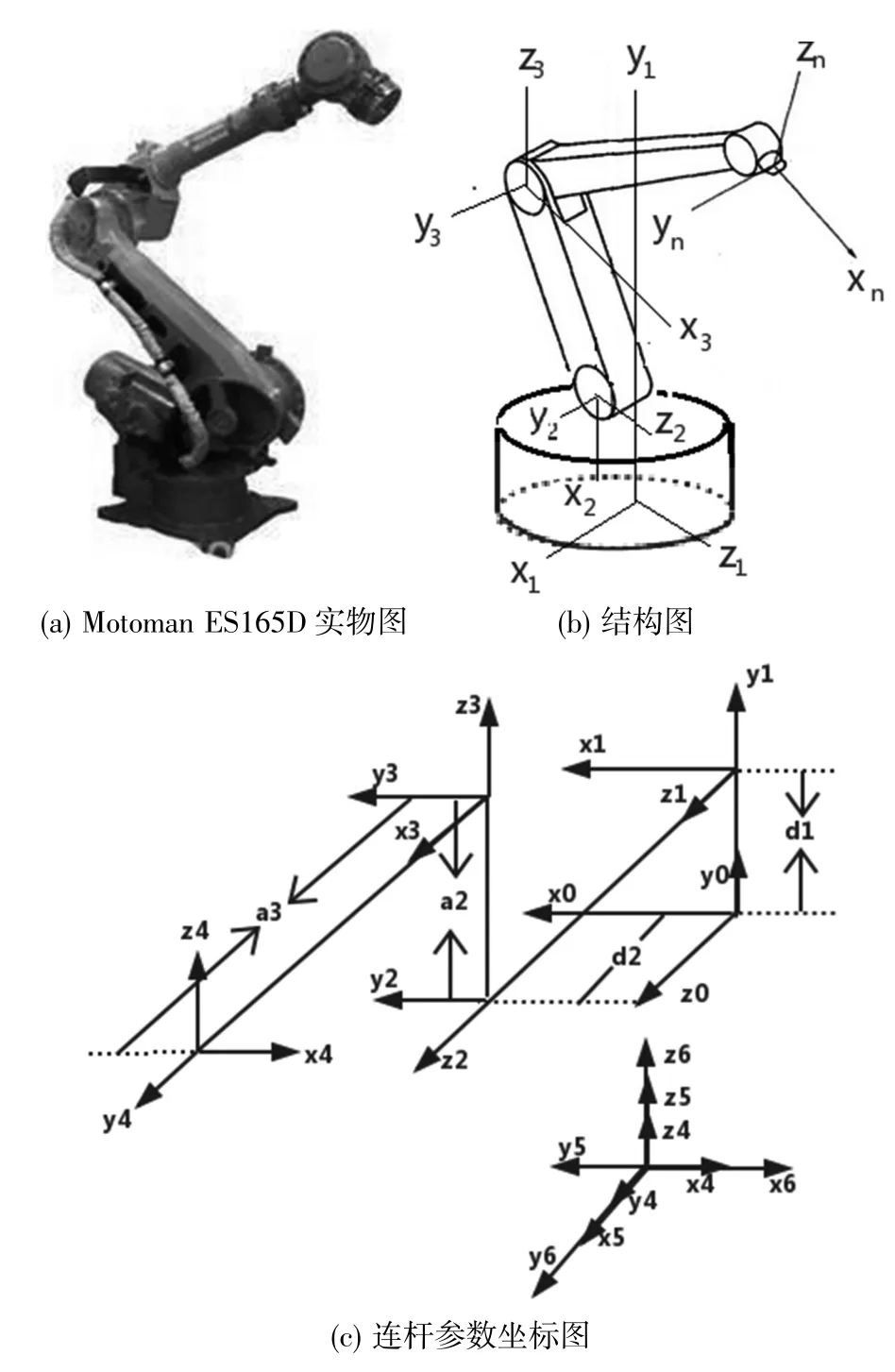
图1 Motoman ES165D型机械臂

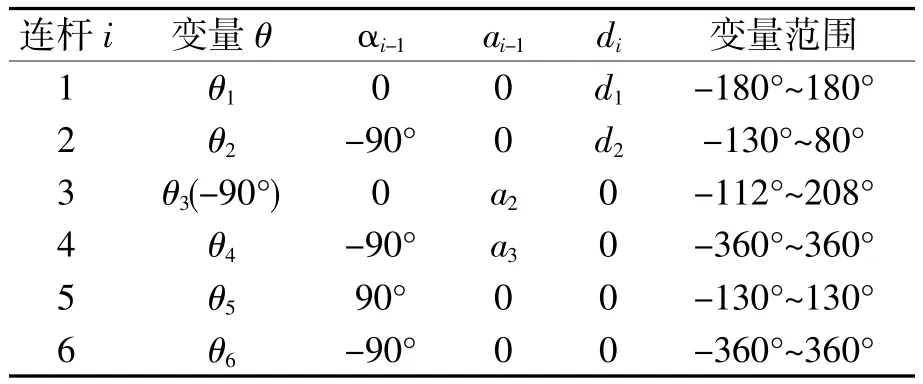
表1 Motoman ES165D机械臂D-H参数

2.2 六自由度串联机械臂反解分析

已知机器人连杆的几何参数，给定机器人末端相对于参考坐标系的期望位置和姿态，通过机器人运动方程的反解，得到机器人能够到达预期位姿的关节变量，这就需要对运动方程求解，即逆运动学。求解θ1时将式(1)等号两边同时左乘得到：

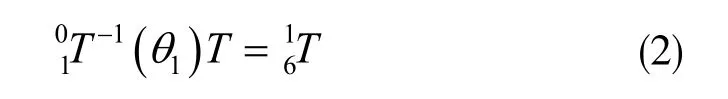
化简可求得：θ1=±90-arctan2(pz,px),式中正、负号对应θ1的两个可能解。

令矩阵方程(2)两边的(2,4)和(3,4)分别对应相等，得到方程组：

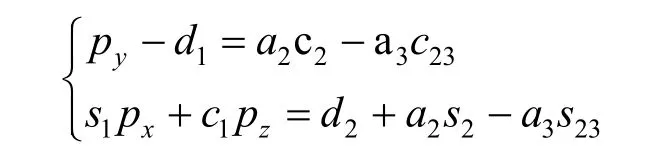
其中s1是sinθ1的缩写，c1是cosθ1的缩写，以此类推，s23=sin(θ2+θ3)，c1=cos(θ2+θ3)，化简得：

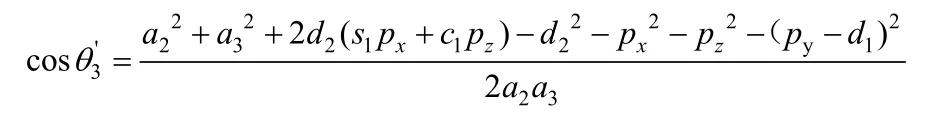
由于θ1存在两个可能解，对应θ3也存在两种可能解。由于结构的限制，根据表1变量的范围，有些解不能实现。故此根据实际情况选择其中一组解来满足机器人的工作要求。

求解θ2时通过矩阵方程：

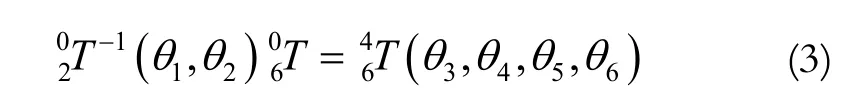
令矩阵方程(3)两端(1,4)对应相等，即有：

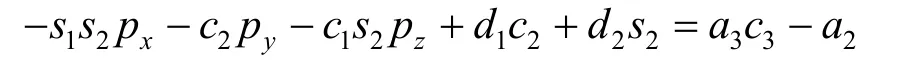
将-a2移到等式左边后对等式两边平方，化简后得：

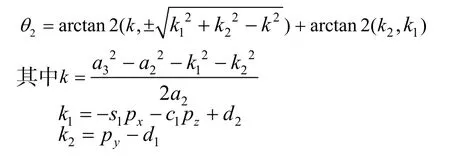
同理可求得θ4,θ5,θ6：

3 干涉判断

3.1 环境模型

在进行干涉判断之前，首先需要对机械臂工作环境进行合理的描述。在干涉判断时采用对环境中的障碍物以及机器人进行两次投影的思想[11-12]。H-平面垂直于机械臂基坐标Y轴轴线；V-平面垂直于H-平面并且经过基坐标Y轴轴线，利用机械臂与障碍物分别在H-平面内以及V-平面内进行投影截取，这样机械臂在三维工作空间中运动的问题便转换为H-平面及V-平面两个平面的二维问题，减少了计算量，提升了系统的实时性。

首先在SolidWorks中对Motoman ES165D机器人本体进行建模，然后应用3D Max对各个关节所在的坐标系进行修改，完成关节间坐标变换的设置。同时利用3D Max中提供的高级建模工具对机器人工作的操作平台、障碍物等相关物件创建模型，最后以FBX格式导入Unity3D中。通过Unity3D自带的物理引擎对零件附加刚体属性，使零件具有质量、摩擦等物理效果，参照生产车间进行虚拟环境搭建，最后搭建了如图2所示的本体模型及环境模型。

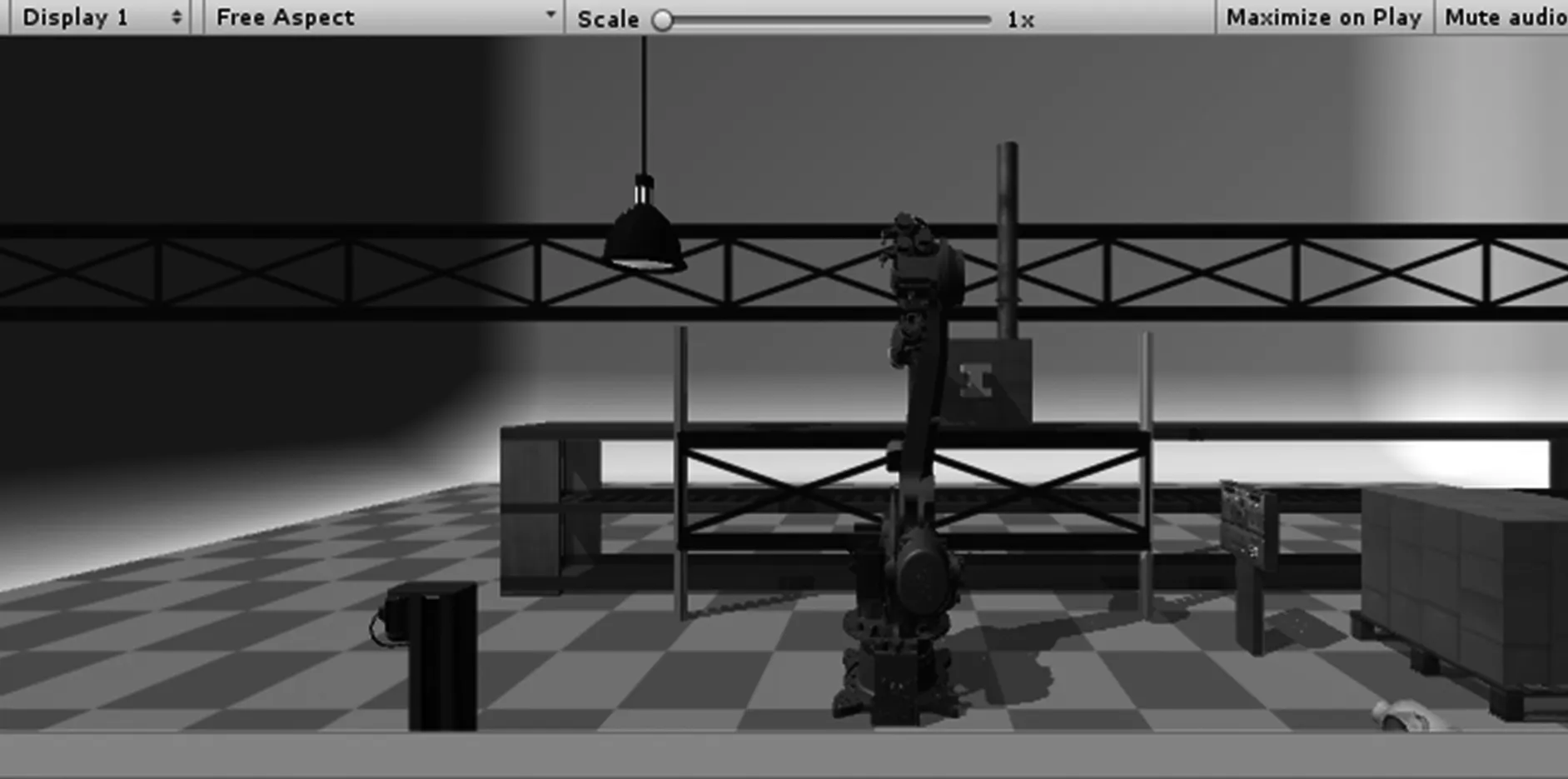
图2 Unity3D工作环境模拟

3.2 连杆之间干涉判断

在串联式机械臂干涉判断方面，因为连杆多为不规则形状，所以将各连杆等效为圆锥或者圆柱形状来简化问题。空间中两连杆干涉情况如图3所示。

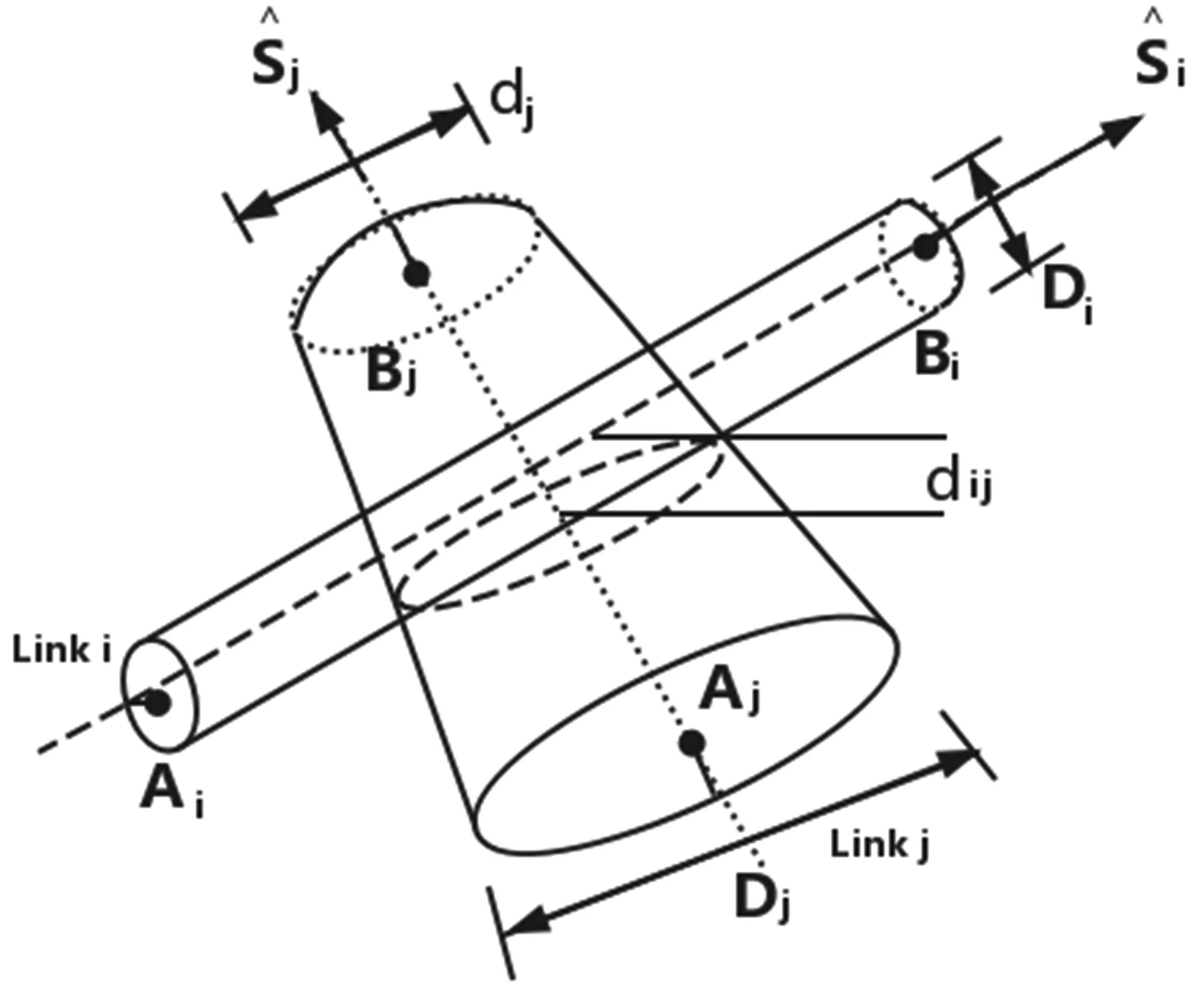
图3 空间中两连杆相互干涉

通过两个连杆之间中心线的垂直距离dij来判断是否发生干涉，其表达式为：

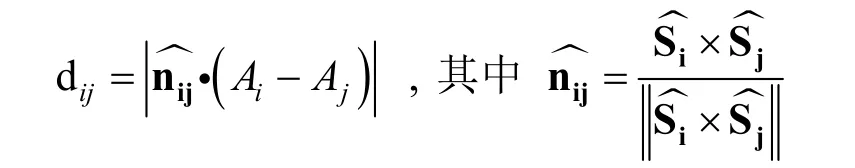
其中dij为两中心线在空间中与公垂线相交两点的距离。为垂直于连杆i与连杆j的单位向量，为两连杆的中心线方向。

空间中两直线Li与Lj的参数方程为：

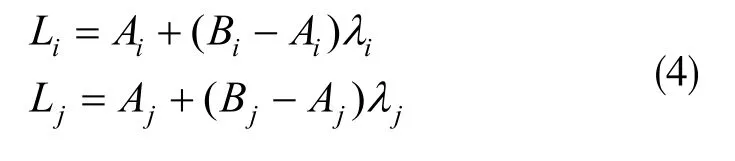
AiBi和AjBj分别为连杆i与连杆j的上下端点的坐标，λi,λj为交点位置参数。两连杆中心线的公垂线与两连杆中心线的交点Qi与Qj，由联立方程求得λi及λj，并分别带回式 (4)求得两交点的位置Qi与Qj。当 0≤λi点位于连杆i长度范围内；当 0≤λj≤1，Qj点位于连杆j长度范围内；所以连杆i与连杆j发生干涉的条件为0≤λi≤1和0≤λj≤1且垂直距离小于干涉点的两杆半径和，以此得到判断条件为：

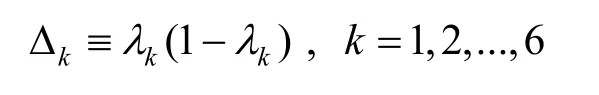
情况一：当Δi≥0，Δj≥0，交点位于i、j连杆范围内,由交点位置参数λj(当λj为0则交点为Aj，直径为Dj;当λj为1则交点为Bj，直径为dj)，则可计算出连杆j在交点位置的直径大小为则发生干涉，否则不发生干涉。

情况二：Δi×Δj＜0，代表交点位于i、j二连杆其中一个的范围内，无法确定是否发生干涉，需要通过求解轴与点的最短距离来作判断，如图4所示。

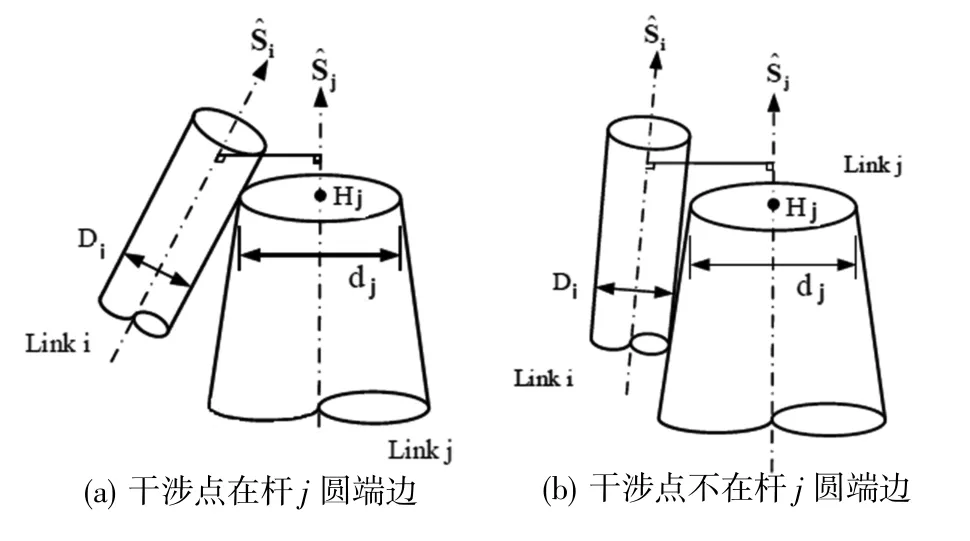
图4 两连杆发生干涉情况二

为了使干涉点固定在障碍物端面的边上，将圆锥体改视为圆柱体来简化判断条件，其直径由大圆Dj取代。利用点到直线最短距离公式来计算，以Δi＞0为例（对于Δj＞0的情况，其求解过程中只需将式中i、j做交换即可），计算结果如下：

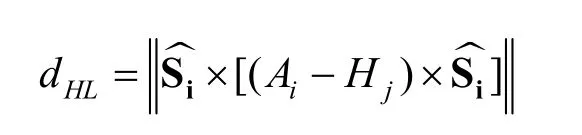
Hj为直线连杆j上点Aj或Bj的坐标，dHL为Hj点到连杆i的最短距离。

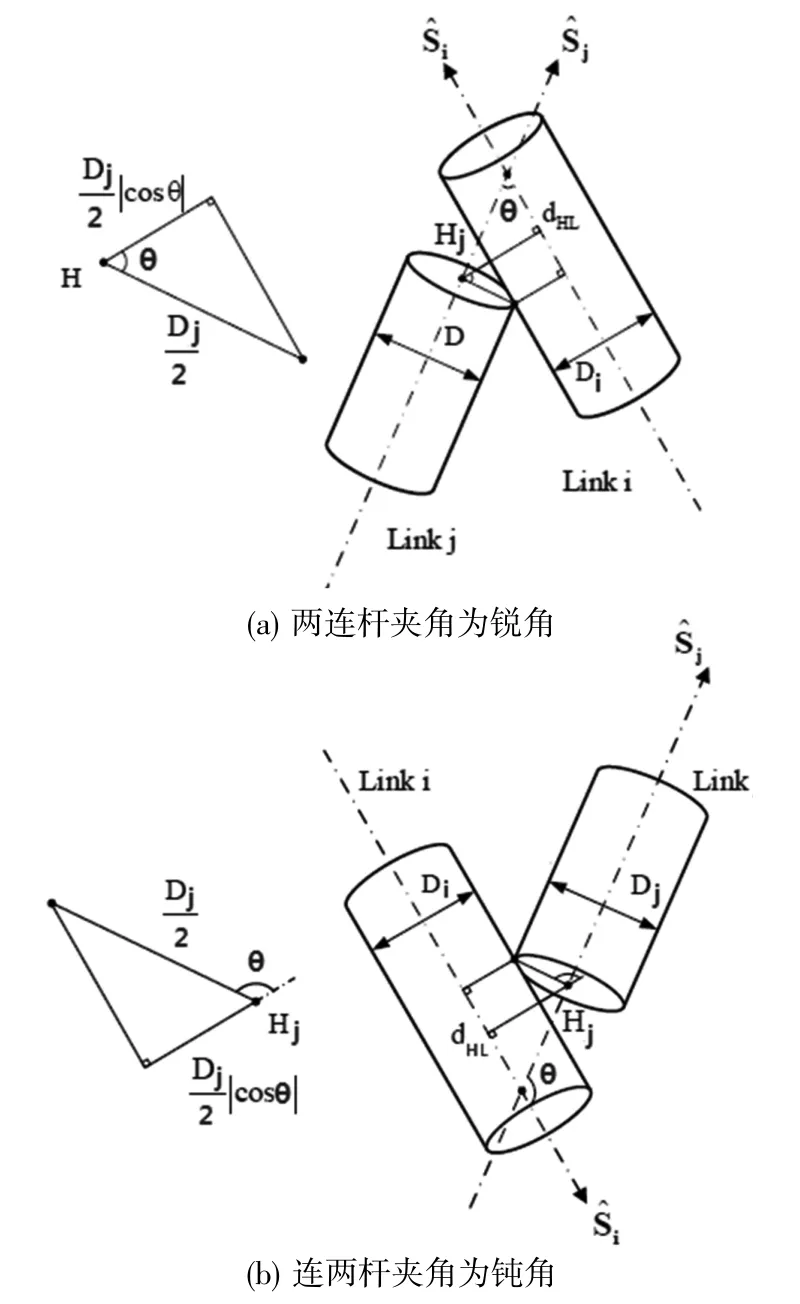
图5 两连杆发生干涉夹角为锐角、钝角情况

情况三：当Δi＜0，Δj＜0，代表连杆i与连杆j的交点都位于两者范围之外。如图6所示，当时，其计算过程与情况二的Δi＞0一样；反之，当时，对其求解只需将式中i、j做交换即可。

3.3 连杆与障碍物之间的干涉判断

第一种方法与连杆之间的干涉判断方法相同，只需将障碍物视为锥柱体或圆柱体进行判别；另外考虑到在现实当中，障碍物多为垂直于水平面的物体，提出第二种较为简易的判断方法：首先，将障碍物设定为圆柱体，圆面的直径为D0；同时也将每根连杆设定为圆柱体，其直径为Di，连杆i的顶点为Ai；而为障碍物的中心线方向，A0为障碍物地面的圆心点，B0为障碍物顶点的圆心点，dOL为连杆2坐标原点O与障碍物中心线在空间中点到直线的距离,其表达式为：

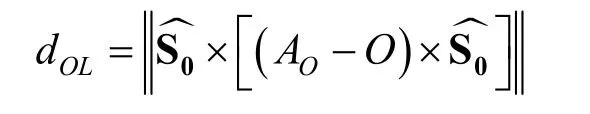
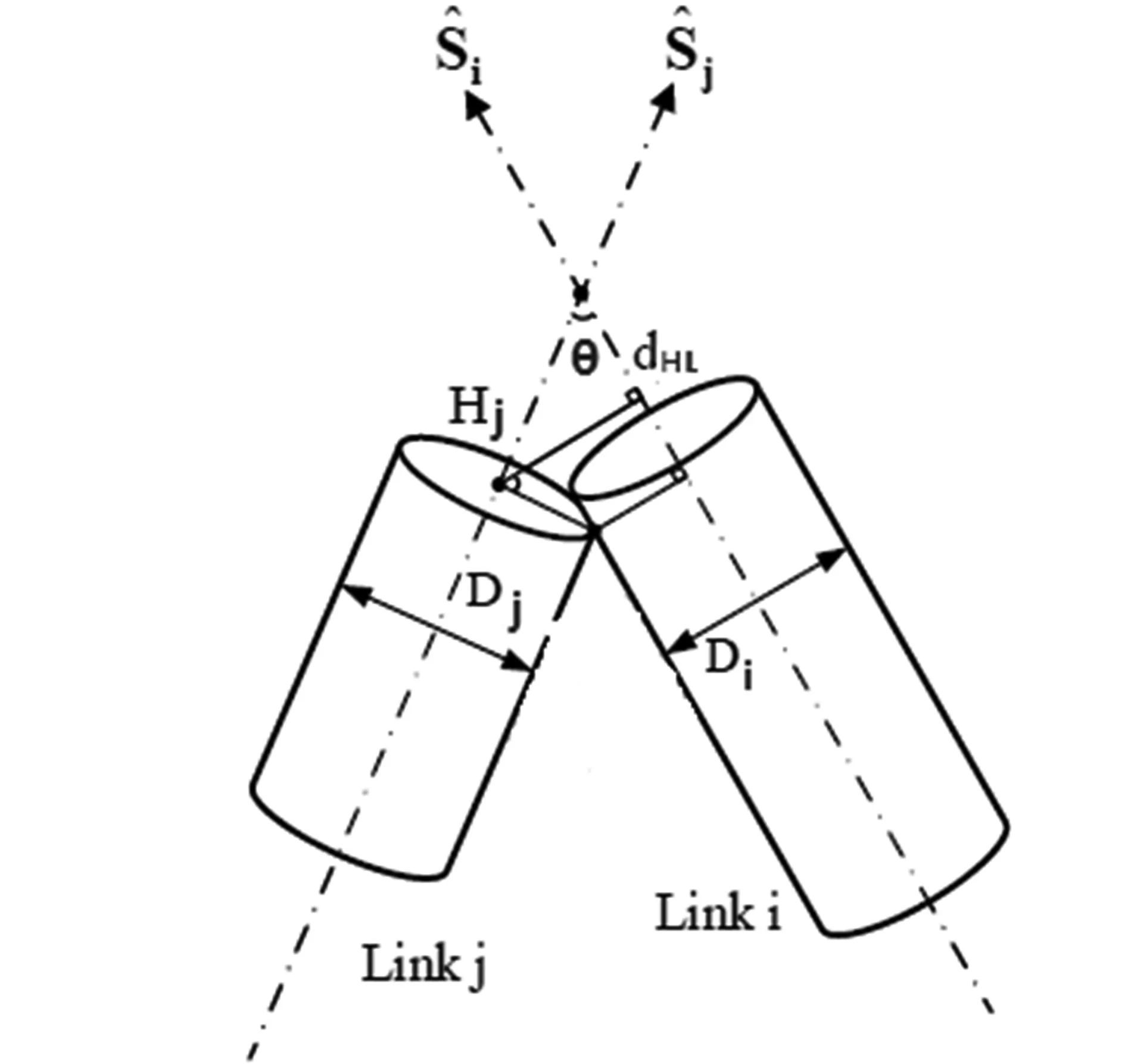
图6 当时，两连杆干涉状况

连杆2与障碍物发生的第一种干涉，将连杆2与障碍物投影到χ-z平面,如图7(a)所示为基坐标原点O与障碍物投影后的圆心C连线与χ轴的夹角，θL2为θ1造成连杆2与障碍物产生干涉的偏转角大小，其表达式为：

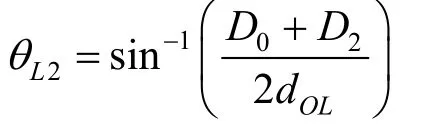
其次，若上述条件成立，需要进一步判断连杆2的长度是否进入障碍物干涉的范围。将连杆2与障碍物都投影到r-y平面，其中r轴为坐标原点O与障碍物底圆圆心A0连线的轴，将连杆2的末端投影至r轴，比较其长度是否有干涉发生。如图7(b)所示，得到连杆2投影到r轴的长度，其中B2r为连杆2投影到r轴的末端点，配合正弦函数将连杆2的直径投影到r轴，得到：

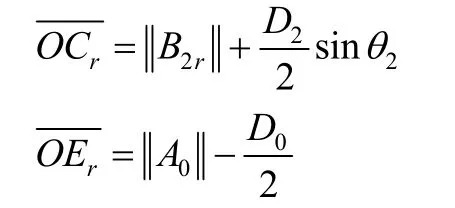
所以当OEr≤OCr，即时，连杆2可能发生干涉，否则不发生干涉。

最后，第二轴角θ2也会影响连杆2与障碍物的干涉状况判定，若上述两个判断条件都成立，同样在r-y平面比较连杆2在y轴方向的高度是否与障碍物发生干涉。如图7(c)所示，其中E为连杆2与障碍物的干涉点，Er为E点投影到r轴的点，Y为连杆2和障碍物的干涉点到连杆2轴的y方向长度：

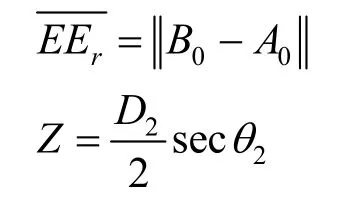
由此得到第三个判断条件：

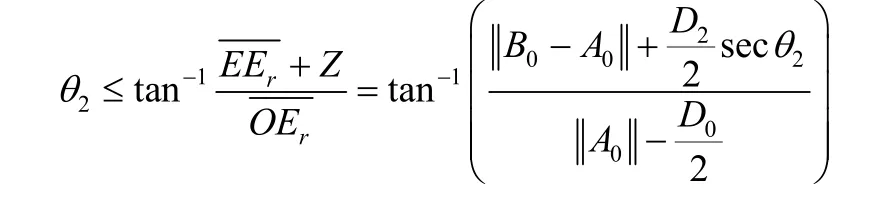
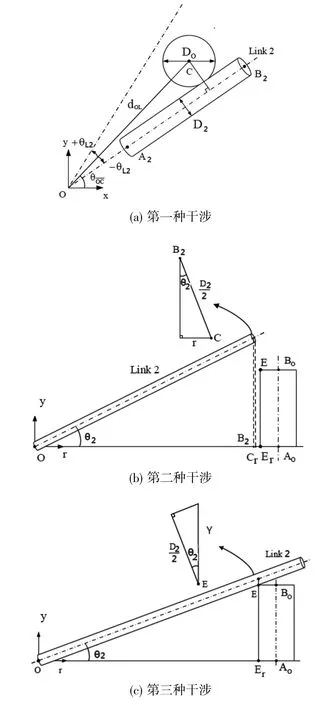
图7 连杆2与障碍物干涉情况

当同时满足上述三个条件时，连杆2发生干涉，否则连杆2无干涉发生。当连杆2无干涉发生时，由于干涉点不一定在连杆2上，所以要继续对连杆3进行干涉判断。

第一步，与连杆2相同，计算连杆3与障碍物之间的造成干涉的偏转角度θL3。

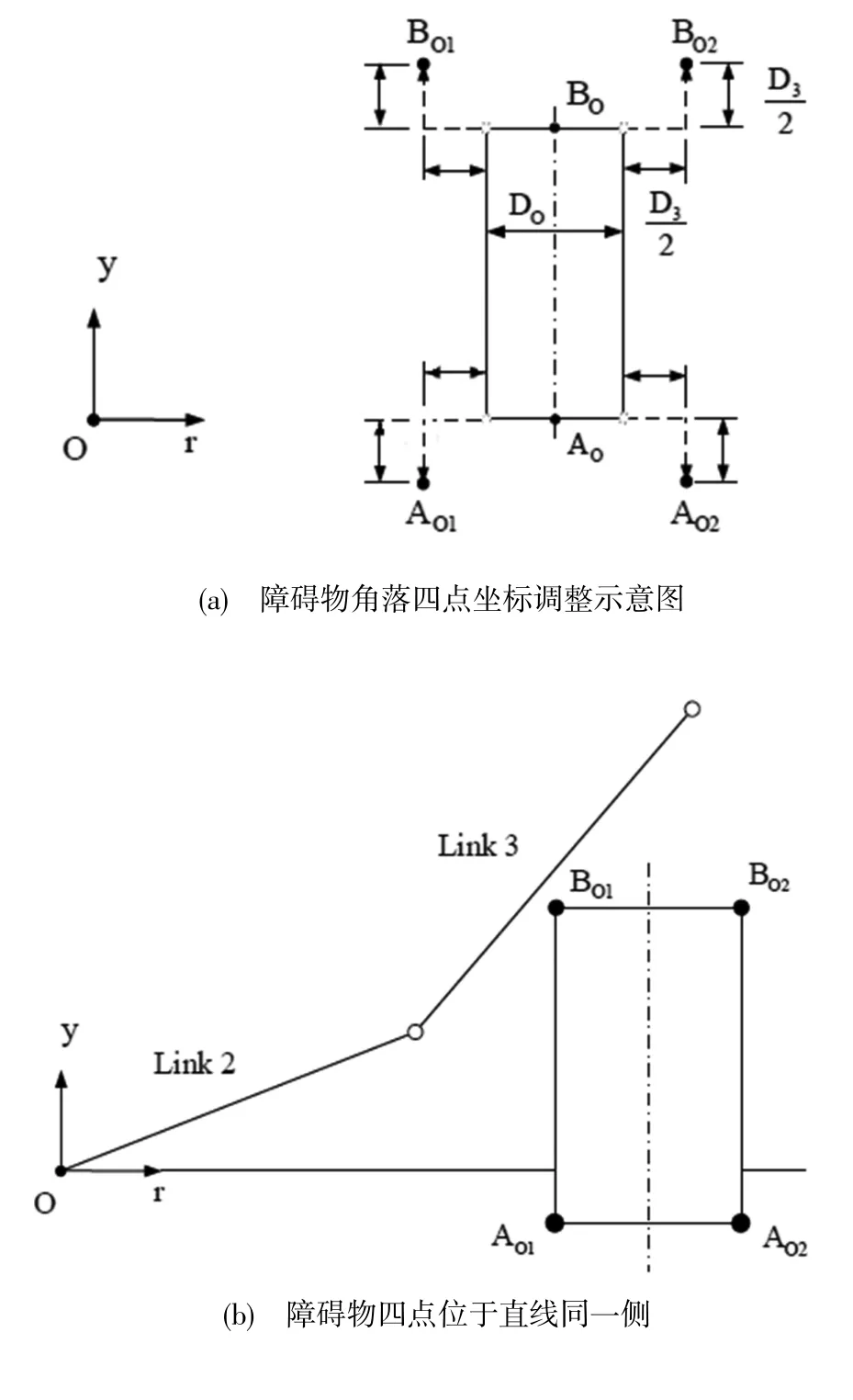
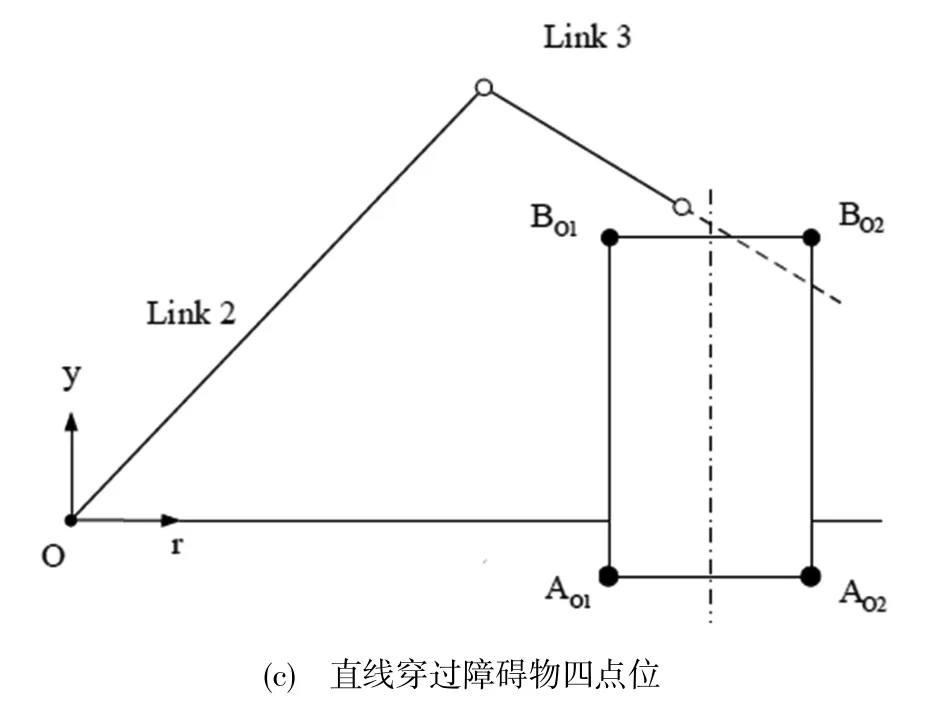
图8 连杆3与障碍物干涉情况

4 仿真实现及结果分析

4.1 基于Unity3D的仿真实现

Unity3D支持C#和JavaScript语言的脚本编程，由于C#语言具有面向对象的特性和强大的函数库，故此选用C#作为开发语言。在仿真初始阶段，为生成相关参数，需要编写Script脚本，用以定义目标点位置、连杆长度等参数，并制成参数控制面板。

根据相关参数对正运动学进行仿真验证，运动学正解的关键代码如下，建立FK类，包含GetMatrix()、MatrixCalcu-Lation()等关键函数：

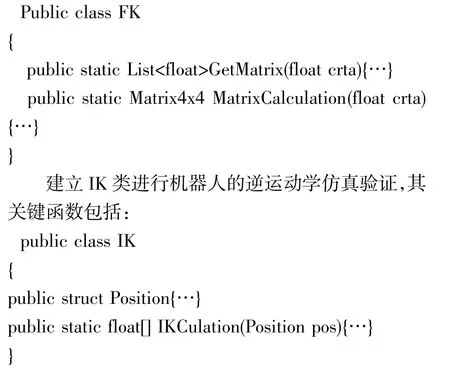
进行正运动学、逆运动学验证之后，编写干涉判断的相关脚本，在Update函数（Update函数是unity提供函数，其在每一帧被调用）中进行条件判断，当发生干涉时输出是哪一连杆发生了干涉。

4.2 结果分析

由于Motoman ES165D型机器人的末端三个关节轴线交于一点，所以只考虑前三个关节干涉的情况。Unity3D中机械臂与障碍物干涉情况如图9。

图9 Unity3D中机械臂与障碍物干涉状况示意图

在已经搭建好的Unity3D环境下，选取机械臂路径中末端点为（11.6,61.5,11.6）的一点，障碍物D0坐标位置为（30,0,-30），障碍物直径为14cm，高度为67cm，通过逆运动学得到每个连杆的旋转角度为：θ1=45°，θ2=45°，θ3=0°，θ4=45°，θ5=30°，θ6=30°。已知每个关节旋转角度之后，利用机器人正运动学得到各个关节在基坐标中的位姿矩阵：

结合连杆参数坐标系，得到连杆2的下端点坐标（14.1,65,14.1），上端点坐标（31.6,89.7,31.6），连杆3下端点坐标（31.6,89.7,31.6），连杆3上端点坐标（11.6,61.5,11.6）。得到各个连杆与障碍物干涉判断状况如表2、表3所示。

表2 各连杆与障碍物第一种判断方法结果数据

表3 各连杆与障碍物的第二种判断方法结果数据

由两表可以看出，两种方法都可以快速地判断出当末端点位于（11.6,61.5,11.6）时，机械臂第三连杆将与障碍物发生碰撞，其中第一种方法较为复杂，须联立两线性方程式求解λ，但其能判断圆锥型障碍物或连杆；第二种方法虽然不能判断圆锥型物体，但其计算量较小，干涉判断速度比第一种方法更快。

5 结束语

将连杆与障碍物简化为更接近实物的圆柱体与圆锥体，通过两种干涉判断法，分析连杆与连杆之间、连杆与障碍物之间干涉发生的可能情况，能够有效判断干涉是否发生及干涉点发生位置，提高了干涉判断精确度。以Motoman ES165D机器人为研究对象，通过分析其结构，构建了本体模型及工作车间场景模型。运用D-H参数法对机器人正逆运动学求解，并在Unity3D中通过虚拟仿真，验证了机器人运动过程中干涉判断方法的可行性，在实际应用中能够有效预防工作中机器人的损坏。